4.4: Relación entre la carga distribuida, la fuerza de corte y el momento de flexión

Para la derivación de las relaciones entre\(w\),, y\(V\)\(M\), considerar una viga simplemente soportada sometida a una carga uniformemente distribuida a lo largo de su longitud, como se muestra en la Figura 4.3. Deje que la fuerza cortante y el momento de flexión en una sección ubicada a una\(x\) distancia del soporte izquierdo sea\(V\) y\(M\), respectivamente, y en una sección\(x + dx\) sea\(V + dV\) y\(M + dM\), respectivamente. La carga total que actúa a través del centro de la longitud infinitesimal es\(wdx\).

\(Fig. 4.3\). Viga simplemente soportada.

Para calcular el momento de flexión en la sección x + dx, utilice lo siguiente:\ [\ begin {aligned}
&M_ {x+d x} =M+V d x-w d x. d x/2\\
&=M+V d x\ text {(descuidando el pequeño término de segundo orden}\ izquierda.w d x^ {2}/2\ derecha)\\
&\ begin {array} {l}
M+d M=M+V d x\\
\ texto {o}\ quad\ frac {d M} {d x} =V (x)
\ end {array}
\ end {alineado}\]

La ecuación 4.1 implica que la primera derivada del momento de flexión con respecto a la distancia es igual a la fuerza de cizallamiento. La ecuación también sugiere que la pendiente del diagrama de momento en un punto determinado es igual a la fuerza de cizallamiento en ese mismo punto. La ecuación 4.1 sugiere la siguiente expresión:\[\Delta M=\int V(x) d x\]

La Ecuación 4.2 establece que el cambio en el momento es igual al área bajo el diagrama de cizallamiento. Del mismo modo, la fuerza de corte en la sección\(x + dx\) es la siguiente:

\(V_{x+d x}=V-w d x\)

\(V+d V=V-w d x\)

o\[\frac{d V}{d x}=-w(x)\]

La ecuación 4.3 implica que la primera derivada de la fuerza de cizallamiento con respecto a la distancia es igual a la intensidad de la carga distribuida. La ecuación 4.3 sugiere la siguiente expresión:\[\Delta V=\int w(x) d x\]

La ecuación 4.4 establece que el cambio en la fuerza de corte es igual al área bajo el diagrama de carga. Las ecuaciones 4.1 y 4.3 sugieren lo siguiente:\[\frac{d^{2} M}{d x^{2}}=-w(x)\]

La ecuación 4.5 implica que la segunda derivada del momento de flexión con respecto a la distancia es igual a la intensidad de la carga distribuida.

Procedimiento de Cómputo de Fuerzas Internas

• Dibuja el diagrama de cuerpo libre de la estructura.
• Verificar la estabilidad y determinación de la estructura. Si la estructura es estable y determinada, proceder al siguiente paso del análisis.
• Determinar las reacciones desconocidas aplicando las condiciones de equilibrio.
• Pasar una sección imaginaria perpendicular al eje neutro de la estructura en el punto donde se van a determinar las fuerzas internas. La sección pasada divide la estructura en dos partes. Considera cualquiera de las partes de la estructura para el cálculo de las fuerzas internas deseadas.
• Para el cálculo de la fuerza axial, determinar la suma de las fuerzas axiales en la parte que se está considerando para su análisis.
• Para el cálculo de la fuerza de corte y momento de flexión, primero escriba la expresión funcional de estas fuerzas internas para el segmento donde se encuentra la sección, con respecto a la distancia\(x\) desde el origen.
• Calcular los valores principales de la fuerza de corte y el momento de flexión en el segmento donde se encuentra la sección.
• Dibuje el diagrama de fuerza axial, fuerza de corte y momento de flexión para la estructura, tomando nota de las convenciones de signos discutidas en la sección 4.3.
• Para las estructuras en voladizo, el paso tres podría omitirse considerando el extremo libre de la estructura como el punto de partida inicial del análisis.

Ejemplo\(\PageIndex{1}\)

Dibuje los diagramas de fuerza de corte y momento de flexión para la viga en voladizo que soporta una carga concentrada en el extremo libre, como se muestra en la Figura 4.4a.

\(Fig. 4.4\). Viga en voladizo.

Solución

Reacciones de apoyo. Primero, computar las reacciones en el soporte. Dado que el soporte at\(B\) es fijo, habrá tres reacciones en ese soporte, a saber,\(B_{y}\), y\(B_{x}\)\(M_{B}\), como se muestra en el diagrama de cuerpo libre en la Figura 4.4b. La aplicación de las condiciones de equilibrio sugiere lo siguiente:

\ (\ begin {array} {c}
\ suma M_ {B} =0:\ quad (5\ mathrm {k}) (3\ mathrm {ft}) -M=0\\
M=15\ mathrm {k}. \ mathrm {ft}\
\ suma F_ {y} =0:\ quad-5\ mathrm {k} +B_ {y} =0\\
B_ {y} =5\ mathrm {k}\\
\ suma F_ {x} =0:\ quad B_ {x} =0
\ end {array}\)

Fuerza de corte (SF).

 

El signo negativo es indicativo de una fuerza de cizallamiento negativa. Esto se debe a que la convención de señal para una fuerza de corte establece que una fuerza transversal descendente a la izquierda de la sección en consideración provocará una fuerza de corte negativa en esa sección.

Diagrama de fuerza de corte. Tenga en cuenta que debido a que la fuerza de corte es una constante, debe ser de la misma magnitud en cualquier punto a lo largo de la viga. Como convención, el diagrama de fuerza de corte se traza por encima o por debajo de una línea correspondiente al eje neutro de la viga, pero se debe indicar un signo más si es una fuerza de cizallamiento positiva, y se debe indicar un signo menos si es una fuerza de cizallamiento negativa, como se muestra en la Figura 4.4c.

Momento de flexión (BM).

Función de momento de flexión. Por definición, el momento de flexión en una sección es la suma de los momentos de todas las fuerzas que actúan a cada lado de la sección. Así, la expresión para el momento de flexión de la\(5k\) fuerza sobre la sección a una distancia x del extremo libre de la viga en voladizo es la siguiente:

\ (\ begin {array} {l}
M=-5 x\
\ text {Cuando} x=0, M=- (5\ mathrm {k}) (0) =0\\
\ text {Cuando} x=3\ mathrm {ft}, M=- (5\ mathrm {k}) (3\ mathrm {ft}) =-15\ mathrm {k}. \ mathrm {ft}
\ end {array}\)

La expresión obtenida es válida para todo el haz (la región\(0 < x < 3\) ft). El signo negativo indica un momento negativo, el cual se estableció a partir de la convención de signos por el momento. Como se ve en la Figura 4.4f, el momento debido a la\(5k\) fuerza tiende a provocar que el segmento de la viga en el lado izquierdo de la sección exhiba una concavidad ascendente, y eso corresponde a un momento de flexión negativo, de acuerdo con la convención del signo para el momento de flexión.

Diagrama de momento de flexión. Dado que la función para el momento de flexión es lineal, el diagrama de momento de flexión es una línea recta. Por lo tanto, es suficiente usar los dos valores principales de los momentos de flexión determinados a\(x = 0\) ft y a\(x = 3\) ft para trazar el diagrama de momento de flexión. Como convención, los diagramas de momento de flexión negativo se trazan debajo del eje neutro de la viga, mientras que los diagramas de momento de flexión positivo se trazan por encima del eje de la viga, como se muestra en la Figura 4.4d.

Ejemplo\(\PageIndex{2}\)

Dibuje los diagramas de fuerza de corte y momento de flexión para la viga en voladizo sometida a una carga uniformemente distribuida en toda su longitud, como se muestra en la Figura 4.5a.

\(Fig. 4.5\). Viga en voladizo.

Solución

Reacciones de apoyo. Primero, computar las reacciones en el soporte. Dado que el soporte at\(B\) es fijo, posiblemente habrá tres reacciones en ese soporte, a saber, y\(B_{y}\)\(B_{x}\)\(M_{B}\), como se muestra en el diagrama de cuerpo libre en la Figura 4.4b. La aplicación de las condiciones de equilibrio sugiere lo siguiente:

\ (\ begin {array} {c}
\ suma M_ {B} =0:\ quad (20\ mathrm {kN}/\ mathrm {m}) (5\ mathrm {~m}) (2.5\ mathrm {~m}) -M=0\\
M=250\ mathrm {kN}\ cdot\ mathrm {m}\
\ suma F_ {y} =0:\ quad- (20\ mathrm {kN}/\ mathrm {m}) (5) +B_ {y} =0\\
B_ {y} =100\ mathrm {kN}\\
\ suma F_ {x} =0:\ quad B_ {x} =0
\ end {array}\)

Fuerza de corte (SF).

Función de fuerza de corte. Sea x la distancia de una sección arbitraria desde el extremo libre de la viga en voladizo, como se muestra en la Figura 4.5b. La fuerza de cizallamiento de todas las fuerzas que actúan sobre el segmento de la viga a la izquierda de la sección, como se muestra en la Figura 4.5e, se determina de la siguiente manera:

\ (\ begin {array} {l}
0<x<5\
V=-20 x\\
\ text {Cuando} x=0, V=0\\
\ texto {Cuando} x=2.5\ mathrm {~m}, V=-50\ mathrm {kN}\
\ text {Cuando} x=5\ mathrm {~m}, V=-100\ mathrm {kN}
\ fin {matriz}\)

La expresión obtenida es válida para toda la viga. El signo negativo indica una fuerza de cizallamiento negativa, la cual se estableció a partir de la convención de signos para una fuerza de cizallamiento. La expresión también muestra que la fuerza de cizallamiento varía linealmente con la longitud de la viga.

Diagrama de fuerza de corte. Tenga en cuenta que debido a que la expresión de la fuerza de corte es lineal, su diagrama consistirá en líneas rectas. Se determinó la fuerza de cizallamiento a\(x = 0\)\(x = 5\) m y m y se utilizó para trazar el diagrama de fuerza de cizallamiento, como se muestra en la Figura 4.5c. Como se muestra en el diagrama, la fuerza de corte varía de cero en el extremo libre de la viga a 100 kN en el extremo fijo. La reacción vertical calculada de\(B_{y}\) en el soporte puede considerarse como una comprobación de la precisión del análisis y diagrama.

Momento de flexión (BM).

Expresión de momento de flexión. La expresión para el momento de flexión en una sección a una\(x\) distancia del extremo libre de la viga en voladizo es la siguiente:

\ (\ begin {array} {l}
0<x<5\ mathrm {~m}\
\\ mathrm {M} =-\ frac {20 x^ {2}} {2}\
\ text {Cuando} x=0, M=0\
\ texto {Cuando} x=2.5\ mathrm {~m}, M=-62.5\ mathrm {kN}. \ mathrm {m}\\
\ texto {Cuando} x=5\ mathrm {~m}, M=-250\ mathrm {kN}. \ mathrm {m}
\ fin {matriz}\)

El signo negativo indica un momento negativo, el cual se estableció a partir de la convención de signos por momento. Como se ve en la Figura 4.5f, el momento debido a la carga distribuida tiende a provocar que el segmento de la viga en el lado izquierdo de la sección exhiba una concavidad ascendente, y eso corresponde a un momento de flexión negativo, de acuerdo con la convención del signo para el momento de flexión.

Diagrama de momento de flexión. Dado que la función para el momento de flexión es parabólica, el diagrama de momento de flexión es una curva. Además de los dos valores principales de momento de flexión en\(x = 0\) m y en\(x = 5\) m, se deben determinar los momentos en otros puntos intermedios para dibujar correctamente el diagrama de momento de flexión. El diagrama del momento de flexión de la viga se muestra en la Figura 4.5d.

Ejemplo\(\PageIndex{3}\)

Dibuje los diagramas de fuerza de corte y momento de flexión para la viga en voladizo sometida a las cargas mostradas en la Figura 4.6a.

\(Fig. 4.6\). Viga en voladizo.

Solución

Reacciones de apoyo. El diagrama de cuerpo libre de la viga se muestra en la Figura 4.6b. Primero, computar las reacciones en el soporte\(B\). La aplicación de las condiciones de equilibrio sugiere lo siguiente:

\ (\ begin {array} {c}
\ suma M_ {B} =0 :( 3\ mathrm {k}/\ mathrm {ft}) (2\ mathrm {ft}) (3\ mathrm {~m}) + (10\ mathrm {k}) (1) -M=0\\
M=28\ mathrm {k}. \ mathrm {ft}\
\ suma F_ {y} =0: -\ izquierda (3\ frac {\ mathrm {k}} {\ mathrm {ft}}\ derecha) (2\ mathrm {ft}) -10\ mathrm {k} +D_ {y} =0\
D_ {y} =16\ mathrm {k}\
\ suma F_ {x} =0: D_ {x} =0
\ end {array}\)

Funciones de fuerza de corte y momento de flexión. Debido a la discontinuidad de la carga distribuida en el punto B y la presencia de la carga concentrada en el punto\(C\), tres regiones describen las funciones de cizallamiento y momento para la viga en voladizo. Las funciones y los valores para la fuerza cortante (\(V\)) y el momento de flexión (\(M\)) en secciones en las tres regiones a una distancia x del extremo libre de la viga son los siguientes:

Segmento\(A B \text{ } 0<x<2\) ft

\(V = -3x\)

Cuando\(x = 0\),\(V = 0\)

Cuando\(x = 1\),\(V = -3\) Kip

Cuando\(x = 2\) ft,\(V = -6\) Kip

\(M=-\frac{3 x^{2}}{2}\)

Cuando\(x = 0\),\(M = 0\)

Cuando\(x = 1\) ft,\(M = -1.5\) kip. ft

Cuando\(x = 2\) ft,\(M = -6\) kip. ft

Segmento\(BC\)\(2 < x < 3\) ft

\(V = -3(2) = -6\)Kip

Cuando\(x = 2\) ft,\(M = -6\) kip. ft

Cuando\(x = 3\) ft,\(M = -12\) kip. ft

Segmento\(CD\)\(3 < x < 4\) ft

\(V=-(3)(2)-10=-16\)kips

\(M=-(3)(2)(x-1)-10(x-3)\)

Cuando\(x = 3\) ft,\(M = -12\) kip. ft

Cuando\(x = 4\) ft,\(M = -28\) kip. ft

La fuerza de cizallamiento calculada se puede verificar en parte con las reacciones de soporte mostradas en el diagrama de cuerpo libre en la Figura 4.6b.

\ (AB\) y es líneas rectas en segmentos\(BC\) y\(CD\). </p">

 

Ejemplo 4.4

Dibuje los diagramas de fuerza de corte y momento de flexión para la viga con un voladizo sometido a las cargas mostradas en la Figura 4.7a.

\(Fig. 4.7\). Viga con voladizo.

Solución

Reacciones de apoyo. Las reacciones en los soportes se muestran en el diagrama de cuerpo libre del haz en la Figura 4.7b. Se computan aplicando las condiciones de equilibrio, de la siguiente manera:

\ (\ begin {array} {l}
+\ curvearrowleft\ suma_ {M_ {A}} =0\\
- (14) (3) - (10) (8) - (8) (8) (4) +B_ {y} (6) =0\\
B_ {y} =63\ text {kips}\ quad\ B_ {y} =63\ uparrow\\
+\ fila derecha\ suma F_ {x} =0\ quad A_ {x} =0\ quad A_ {x} = 0\\
+\ uparrow\ suma F_ {y} =0\\
63+A_ {y} -14-10- (8) (8) =0\\
A_ {y} =25\ texto {kips}\ quad\ quad A_ {y} = 25\ texto {kips}\ uparrow
\ end {array}\)

Funciones de cizallamiento y momento de flexión. Debido a la carga concentrada en el punto\(B\) y la porción en voladizo\(CD\), se consideran tres regiones para describir la fuerza de cizallamiento y las funciones de momento de flexión para la viga en voladizo. La expresión para estas funciones en secciones dentro de cada región y los valores principales en los puntos finales de cada región son los siguientes:

\(0 < x < 3\)

 

Cuando\(x = 0\),\(V = 25\) kips

Cuando\(x = 3\),\(V = 1\) Kip

\(M=25 x-\frac{8 x^{2}}{2}\)

Cuando\(x = 0\),\(M = 0\)

Cuándo\(x = 3\),\(M = 39\) kip. ft

\(3 < x < 6\)

 

Cuando\(x = 3\),\(V = -13\) kips

Cuando\(x = 6\),\(V = -37\) kips

\(M = 25 x-14(x-3)-\frac{8 x^{2}}{2}\)

Cuando\(x = 3\),\(M = 39\) k. ft

Cuándo\(x = 6\),\(M = -36\) kip. ft

\(0 < x < 2\)

\(V=10+8 x\)

Cuando\(x = 0\),\(V = 10\) kips

Cuando\(x = 2\),\(V = 26\) kips

\(M = 10 x-\frac{8 x^{2}}{2}\)

Cuando\(x = 0\),\(M = 0\)

Cuándo\(x = 2\),\(M = -36\) kip. ft

Diagrama de fuerza de corte y momento de flexión. La fuerza de cizallamiento determinada y el diagrama de momento en los puntos finales de cada región se representan gráficamente en la Figura 4.7c y la Figura 4.7d. Para un trazado preciso de la curva del momento de flexión, a veces es necesario determinar algunos valores del momento de flexión en puntos intermedios insertando algunas distancias dentro de la región en la función obtenida para esa región. Observe que en la ubicación de las cargas concentradas y en los soportes, los valores numéricos del cambio en la fuerza de cizallamiento son iguales a la carga concentrada o reacción.

Ejemplo 4.5

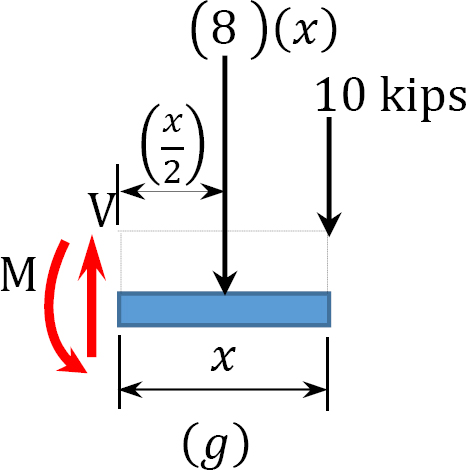
Dibuje los diagramas de fuerza de corte y momento de flexión para la viga con un voladizo sometido a las cargas mostradas en la Figura 4.8a. Determinar la posición y la magnitud del momento máximo de flexión.

\(Fig. 4.8\). Viga con voladizo.

Solución

Reacciones de apoyo. Las reacciones en los soportes del haz se muestran en el diagrama de cuerpo libre en la Figura 4.8b. Las reacciones se computan aplicando las siguientes ecuaciones de equilibrio:

\ (\ begin {array} {l}
+\ curvearrowleft\ sum M_ {A} =0\\
-\ left (\ frac {1} {2}\ right) (4) (10)\ left (\ frac {2} {3}\ times 4\ right) - (2) (1.5) (4.75) + (4) B_ {y} =0\\
B_ {y} =16.90\ mathrm {kN}\ uparrow\\
+\ uparrow\ suma F_ {y} =0\\
A_ {y} +16.90-\ left (\ frac {1} {2} \ derecha) (4) (10) - (2) (1.5) =0\\
A_ {y} =6.10\ mathrm {kN}\ uparrow\\
+\ fila derecha\ suma_ {x} =0\
A_ {x} =0
\ end {array}\)

Funciones de cizallamiento y momento de flexión. Debido a la discontinuidad en los tonos de las cargas distribuidas en el soporte\(B\),\(x\) se consideran dos regiones de para las funciones de descripción y momento, como se muestra a continuación:

\(0 < x < 4\)

\(V = 6.10-\left(\frac{1}{2}\right)(x)\left(\frac{10 x}{4}\right)\)

Cuando\(x = 0\),\(V = 6.10\) kN

Cuando\(x = 2\),\(V = 1.1\) kN

Cuando\(x = 4\),\(V = -13.9\) kN

\(M = 6.10 x-\left(\frac{1}{2}\right)(x)\left(\frac{10 x}{4}\right)\left(\frac{1}{3} x\right)\)

Cuando\(x = 0\),\(M = 0\)

Cuando\(x = 2\),\(M = 8.87\) Kn. m

Cuando\(x = 4\),\(M = -2.3\) Kn. m

\(0 < x < 1.5\)

\(V = 2x\)

Cuando\(x = 0\),\(V = 0\)

Cuando\(x = 1.5\),\(V = 3\) kN

\(M=-(2)(x)\left(\frac{x}{2}\right)\)

Cuando\(x = 0\),\(M = 0\)

Cuando\(x = 1.5\) m,\(M = -2.3\) kn. m

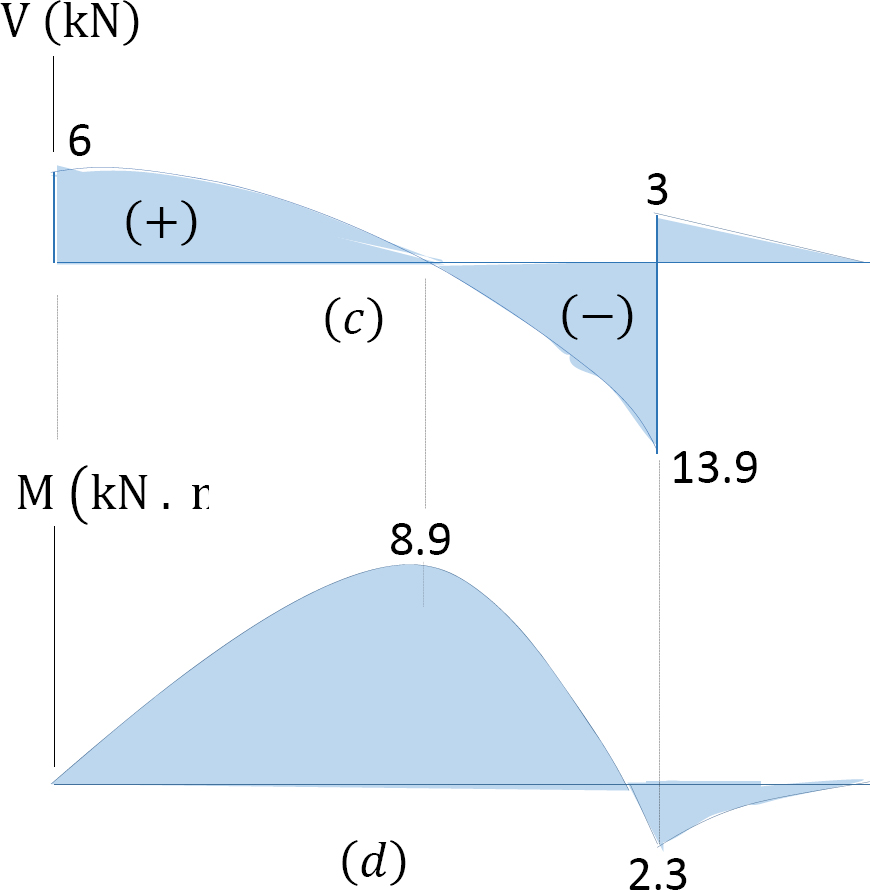
Diagramas de fuerza de corte y momento de flexión. Los valores calculados de la fuerza de cizallamiento y el momento de flexión se representan en la Figura 4.8c y la Figura 4.8d. Observe que los valores de la fuerza de cizallamiento en los soportes son iguales a los valores de las reacciones de soporte. Además, observe en el diagrama que la cizalla en la región\(AB\) es una curva y la cizalla en la región\(BC\) es una recta, todas las cuales corresponden a las funciones parabólica y lineal respectivamente obtenidas para las regiones. Los diagramas de momento de flexión para ambas regiones son curvilíneos. La curva para la\(AB\) región es más profunda que la de la\(BC\) región. Esto se debe a que la función obtenida para la\(AB\) región es cúbica mientras que la de la\(BC\) región es parabólica.

Posición y magnitud del momento máximo de flexión. El momento máximo de flexión ocurre donde la fuerza de corte es igual a cero. Como se muestra en el diagrama de fuerza de corte, el momento máximo de flexión ocurre en la porción\(AB\). Equiparar la expresión de la fuerza de cizallamiento para esa porción como igual a cero sugiere lo siguiente:

\ (\ begin {array} {l}
V=6.10-\ frac {10 x^ {2}} {8} =0\\
x=\ sqrt {\ frac {(6.1) (8)} {10}} =2.21\ mathrm {~m}
\ end {array}\)

La magnitud del momento de flexión máximo se puede determinar poniendo\(x = 2.21\) m en la expresión para el momento de flexión para la porción\(AB\). Por lo tanto,

\(M_{\max }=6.10 x-\left(\frac{1}{2}\right)(x)\left(\frac{10 x}{4}\right)\left(\frac{1}{3} x\right)=(6.1)(2.21)-\frac{(10)\left(2.21^{3}\right)}{24}=8.98 \mathrm{kN} \cdot \mathrm{m}\)

Ejemplo 4.6

Dibuje los diagramas de fuerza de corte y momento de flexión para la viga compuesta sometida a las cargas mostradas en la Figura 4.9a.

\(Fig. 4.9\). Haz compuesto.

Solución

Diagrama de cuerpo libre. El diagrama de cuerpo libre de la viga se muestra en la Figura 4.9b.

Clasificación de la estructura. El haz compuesto tiene\(r = 4\),\(m = 2\), y\(f_{i}=2\). Ya que\(4 + 2 = 3(2)\), la estructura está determinada estáticamente.

Identificación de la estructura primaria y complementaria. El diagrama esquemático de la interacción del miembro para el haz se muestra en la Figura 4.9c. La parte\(AC\) es la estructura primaria, mientras que la parte\(CD\) es la estructura complementaria.

Análisis de estructura complementaria.

Reacción de soporte.

\(C_{y}=D_{y}=25 \mathrm{kN}\), debido a la simetría de carga.

Fuerza de corte y momento de flexión.

\(0 < x < 0.5\)

\(V = 25\)kN

\(M = 25x\)

Cuando\(x = 0\),\(M = 0\)

Cuando\(x = 0.5\),\(M = 12.5\) Kn. m

Análisis de la estructura primaria.

Reacciones de apoyo.

\ (\ begin {array} {l}
+\ curvearrowleft\ suma M_ {A} =0\\
2 B_ {y} - (14) (3) (1.5) - (25) (3) =0\
B_ {y} =69\ mathrm {kN}\ uparrow\\
+\ uparrow\ uparrow\ suma F_ {y} =0\\
69+A+_ {y} -25- (14) (3) =0\\
A_ {y} =-2\ mathrm {kN}
\ end {array}\)

Lo negativo implica la reacción a los\(A\) actos a la baja.

\ (\ begin {array} {l}
+\ fila derecha\ suma F_ {x} =0\\
A_ {x} =0
\ end {array}\)

Funciones de fuerza cortante y momento de flexión.

\(0 < x < 1\)

\(V = 25 + 14x\)

Cuando\(x = 0\),\(V = 25\) kN

Cuando\(x = 1\),\(V = 39\) kN

 

Cuando\(x = 0\),\(M = 0\)

Cuando\(x = 1\),\(M = -32\) Kn. m

\(0 < x < 2\)

\(V = −2 − 14x\)

Cuando\(x = 0\),\(V = -2\) kN

Cuando\(x = 2\),\(V = -30\) kN

 

Cuando\(x = 0\),\(M = 0\)

Cuando\(x = 2\),\(M = -32\) Kn. m

Diagramas de fuerza de corte y momento de flexión. Los valores calculados de la fuerza de cizallamiento y el momento de flexión para la parte primaria y complementaria de la viga compuesta se representan en la Figura 4.9d y la Figura 4.9e.

Ejemplo 4.7

Dibuje los diagramas de fuerza cortante y momento de flexión para el marco sometido a las cargas mostradas en la Figura 4.10a.

\(Fig. 4.10\). Marco.

Solución

Diagrama de cuerpo libre. El diagrama de cuerpo libre de la viga se muestra en la Figura 4.10a.

Reacciones de apoyo. Las reacciones en el soporte del haz se pueden computar de la siguiente manera al considerar el diagrama de cuerpo libre y usar las ecuaciones de equilibrio:

\(\begin{array}{l} +\uparrow \sum F_{y}=0 \\ A_{y}-20=0 \\ A_{y}=20 \mathrm{kN} \uparrow \\ +\rightarrow \sum F_{x}=0 \\ -A_{x}+\left(\frac{1}{2} \times 10 \times 10\right)=0 \\ A_{x}=50 \mathrm{kN} \leftarrow \\ +\curvearrowleft \sum M_{A}=0 \\ M_{A}-20(3)-\left(\frac{1}{2} \times 10 \times 10\right)\left(\frac{1}{3} \times 10\right)=0 \\ M_{A}=226.67 \mathrm{kN} . \mathrm{m} \curvearrowleft \end{array}\)

Funciones de fuerza de corte y momento de flexión de la viga\(BC\).

\(0 < x_{1} < 3\)

\(V = 0\)

\(M = 0\)

\(3 < x_{2} < 6\)

\(V = 20 \mathrm{kN}\)

\(M = −20 (x − 3)\)

Cuando\(x = 3\),\(M = 0\)

 

Tenga en cuenta que la distancia\(x\) a la sección en las expresiones es desde el extremo derecho de la viga.

Funciones de fuerza de corte y momento de flexión de la columna\(AB\).

\(0 < x_{3} < 10\)

\(V =\left(\frac{1}{2} \times x \times x\right)\)

Cuando\(x = 0\),\(V = 0\)

Cuando\(x = 10\),\(V = 50 \mathrm{kN}\)

\(M = -20(3)-\left(\frac{1}{2} \times x \times x\right)\left(\frac{x}{3}\right)\)

 

Cuando\(x = 10\),\(M = -226.67 \mathrm{kN}\) Kn. m

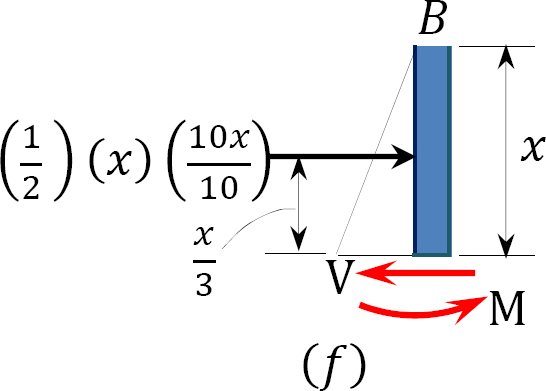
Obsérvese que la distancia\(x\) a la sección de la columna es desde la parte superior de la columna y que se utilizó un triángulo similar para determinar la intensidad de la carga triangular en la sección de la columna, de la siguiente manera:\(\frac{x}{10}=\frac{w}{(10)} \text { or } w=\frac{(10 x)}{10}\).

Diagramas de fuerza de corte y momento de flexión. Los valores calculados de la fuerza de corte y el momento de flexión para el marco se representan como se muestra en la Figura 4.10c y la Figura 4.10d.

Ejemplo 4.8

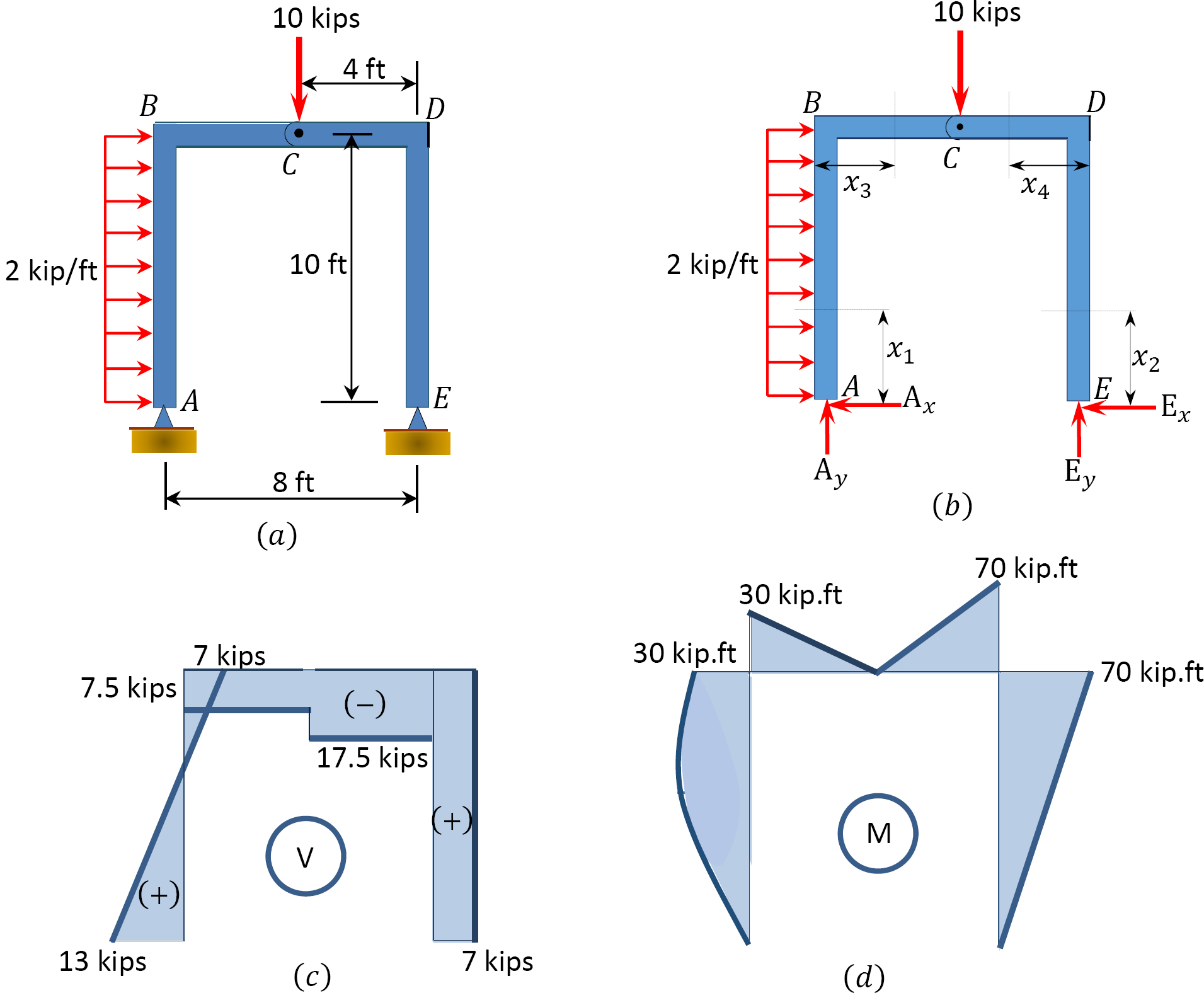
Dibuje los diagramas de fuerza de corte y momento de flexión para el marco sometido a las cargas mostradas en la Figura 4.11a.

\(Fig. 4.11\). Marco.

Solución

Diagrama de cuerpo libre. El diagrama de cuerpo libre de la viga se muestra en la Figura 4.11b.

Reacciones de apoyo. Las reacciones en los soportes del marco se pueden calcular considerando el diagrama de cuerpo libre de todo el fotograma y parte del marco. Las reacciones verticales de los soportes en puntos\(A\) y\(E\) se computan considerando el equilibrio de todo el marco, de la siguiente manera:

\ (\ begin {array} {l}
+\ curvearrowleft\ sum M_ {A} =0\\
-2 (10)\ left (\ frac {10} {2}\ derecha) -10 (4) +E_ {y} (8) =0\\
E_ {y} =17.5\ text {kips}\ quad E_ {y} =17.5\ text {kips}\ uparrow\\
+\ uparrow\ suma F_ {y} =0\\
A_ {y} +17.5-10=0\\
A_ {y} =-7.5\ texto {kips}\ quad A_ {y} =7.5\ texto {kips}\ flecha abajo
\ fin {array}\)

El signo negativo indica que\(A_{y}\) actúa hacia abajo en lugar de hacia arriba como se suponía originalmente.

Considerando el equilibrio de parte\(CDE\) del marco, la reacción horizontal del soporte en\(E\) se determina de la siguiente manera:

\ (\ begin {array} {l}
+\ curvearrowleft\ sum M_ {C} =0\\
17.5 (4) -E_ {x} (10) =0\\
E_ {x} =7\ mathrm {kips}\ fila izquierda\ quad E_ {x} =7\ mathrm {kips}\ izquierda
\ final {array}\)

Nuevamente, considerando el equilibrio de todo el marco, la reacción horizontal at\(A\) puede calcularse de la siguiente manera:

\ (\ begin {array} {l}
+\ fila derecha\ suma F_ {x} =0\\
-A_ {x} +2 (10) -7=0\\
A_ {x} =13\ texto {kips}\ fila izquierda\ quad A_ {x} =13\ texto {kips}\ fila izquierda
\ final {array}\)

Momento de cizallamiento y flexión de las columnas del marco.

Fuerza de corte y momento de flexión en columna\(AB\).

\(0 < x_{1} < 10\)ft

\(V = 13 − 2x\)

Cuando\(x = 0\),\(V = 13\) kips

Cuando\(x = 10\) pies,\(V = -7\) kips

\(M = 13 x-2\left(\frac{x^{2}}{2}\right)\)

Cuando\(x = 0\),\(M = 0\)

Cuando\(x = 10\) ft,\(M = 30\) kip. ft

Cuando\(x = 5\) ft,\(M = 30\) kip. ft

Fuerza de corte y momento de flexión en columna\(ED\) .

\(0 < x_{2} < 10\)ft

\(V = 7\)kips

\(M = 7x\)

Cuando\(x = 0\),\(M = 0\)

Cuando\(x = 10\) ft,\(M = 70\) kip. ft

Momento de cizallamiento y flexión de la viga del marco.

Fuerza de corte y momento de flexión en viga\(BC\).

\(0 < x_{3} < 4\)ft

\(V = −7.5\)kips

\(M=-7.5 x+13(10)-2(10)\left(\frac{10}{2}\right)\)

Cuándo\(x = 0\),\(M = 30\) kip.ft

Cuando\(x = 4\) ft,\(M = 0\)

Fuerza de corte y momento de flexión en viga\(CD\).

\(0 < x_{4} < 4\)ft

\(V = −17.5\)kips

\(M=17.5 x-7(10)\)

Cuándo\(x = 0\),\(M = -70\) kip.ft

Cuando\(x = 4\) ft,\(M = 0\)

Los valores calculados de la fuerza de corte y el momento de flexión para el marco se representan en la Figura 4.11c y la Figura 4.11d.

Resumen del Capítulo

Fuerzas internas en vigas y bastidores: Cuando una viga o marco se somete a fuerzas y momentos transversales externos, se desarrollan tres fuerzas internas en el miembro, a saber, la fuerza normal (\(N\)), la fuerza de cizallamiento (\(V\)) y el momento de flexión (\(M\)). Estos se muestran en la siguiente Figura.

Fuerza normal: La fuerza normal en cualquier sección de una viga se puede determinar sumando las fuerzas horizontales normales que actúan a ambos lados de la sección. Si la resultante de la fuerza normal tiende a moverse hacia la sección, se considera como compresión y se denota como negativa. No obstante, si tiende a alejarse de la sección, se le considera tensión y se denota como positiva.

Fuerza cortante: La fuerza cortante en cualquier sección de una viga se determina como la suma de todas las fuerzas transversales que actúan a cada lado de la sección. La convención de signos adoptada para las fuerzas de cizallamiento está a continuación. Un diagrama que muestra la variación de la fuerza de corte a lo largo de una viga se denomina diagrama de fuerza de corte.

Momento de flexión: El momento de flexión en una sección de una viga se puede determinar resumiendo el momento de todas las fuerzas que actúan a ambos lados de la sección. La convención de signos para momentos de flexión se muestra a continuación. Una representación gráfica del momento de flexión que actúa sobre la viga se conoce como el diagrama de momento de flexión.

Relación entre carga distribuida, fuerza cortante y momento de flexión: Existe la siguiente relación entre cargas distribuidas, fuerzas de corte y momentos de flexión.

\ (\ comenzar {alineado}
\ frac {d V} {d x} &=w\
\ Delta V &=\ int w d x\
\ frac {d M} {d x} &=V\
\ Delta M &=\ int V d x\
\ frac {d^ {2} M} {d x^ {2}} &=W
\ final {alineado}\)

Problemas de práctica

4.1. Dibuje la fuerza de corte y los diagramas de momento de flexión para las vigas mostradas en la Figura P4.1 a la Figura P4.11.

\(Fig. P4.1\). Viga.

\(Fig. P4.2\). Viga.

\(Fig. P4.3\). Viga.

\(Fig. P4.4\). Viga.

\(Fig. P4.5\). Viga.

\(Fig. P4.6\). Viga.

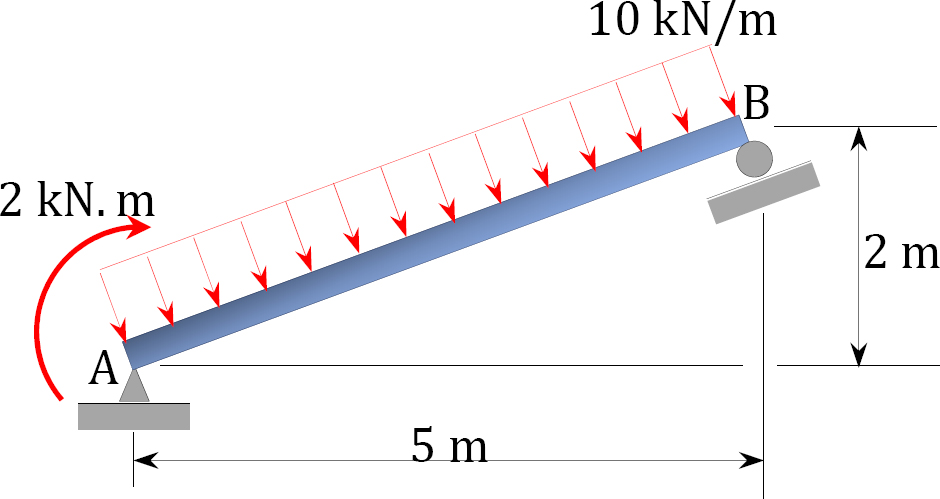
\(Fig. P4.7\). Viga.

\(Fig. P4.8\). Viga.

\(Fig. P4.9\). Viga.

\(Fig. P4.10\). Viga.

\(Fig. P4.11\). Viga.

4.2. Dibuje la fuerza de corte y los diagramas de momento de flexión para los marcos mostrados en la Figura P4.12 a la Figura P4.19.

\(Fig. P4.12\). Marco.

\(Fig. P4.13\). Marco.

\(Fig. P4.14\). Marco.

\(Fig. P4.15\). Marco.

\(Fig. P4.16\). Marco.

\(Fig. P4.17\). Marco.

\(Fig. P4.18\). Marco.

\(Fig. P4.19\). Marco.