11.6: Análisis de Marcos Indeterminados

Los marcos indeterminados se categorizan como marcos con o sin desplazamiento lateral. Un marco con inclinación lateral es aquel que permite un momento lateral o un vaivén hacia un lado debido a la naturaleza asimétrica de su estructura o carga. El análisis de marcos sin oscilaciones laterales es similar al análisis de haces considerados en la sección anterior, mientras que el análisis de marcos con oscilaciones laterales requiere tomar en consideración el efecto del movimiento lateral de la estructura.

Análisis de Marcos con Side-Sway

Considere el marco que se muestra en la Figura 11.6 para una ilustración del efecto de la inclinación lateral en un marco. Debido a la aplicación asimétrica de las cargas, habrá un desplazamiento lateral\(\Delta\) hacia la derecha en\(B\) y\(C\), que posteriormente provocará rotaciones de cuerdas\(\psi_{A B}\left(\frac{\Delta}{L_{A B}}\right)\) y\(\psi_{D C}\left(\frac{\Delta}{L_{D C}}\right)\) en columnas\(AB\) y\(DC\), respectivamente. Estas rotaciones deben ser consideradas al escribir las ecuaciones pendiente-deflexión para las columnas, como se demostrará en los ejemplos resueltos.

\(Fig. 11.6\). Marco.

Ejemplo 11.1

Mediante el método pendiente-deflexión, se determinan los momentos finales y las reacciones en los soportes de la viga que se muestran en la Figura 11.7a y se dibujan los diagramas de fuerza de cizallamiento y momento de flexión. \(EI\)= constante.

\(Fig. 11.7\). Viga.

Solución

Momentos de extremo fijo.

Los momentos de extremo fijo (FEM) usando la Tabla 11.1 se calculan de la siguiente manera:

\ (\ begin {array} {l}
F E M_ {A B} =-\ frac {w\ mathrm {~L} ^ {2}} {12} =-\ frac {65\ times 4^ {2}} {12} =-86.67\ mathrm {kN}. \ mathrm {m}\\
F E M_ {B A} =\ frac {w\ mathrm {~L} ^ {2}} {12} =86.67\ mathrm {kN}. \ mathrm {m}\\
F E M_ {B C} =-\ frac {35\ times 4^ {2}} {12} =-46.67\ mathrm {kN}. \ mathrm {m}\\
F E M_ {C B} =46.67\ mathrm {kN}. \ mathrm {m}
\ fin {matriz}\)

Ecuaciones de deflexión en pendiente. \(\delta_{A} = \delta_{C} = 0\)Debido a la fijedad en ambos extremos y\(\psi_{A B}=\psi_{B C}=0\) como no ocurre ningún asentamiento, las ecuaciones para los momentos finales de los miembros se expresan de la siguiente manera:

\ [\ begin {array} {c}
M_ {A B} =\ frac {2\ mathrm {EI}} {L}\ left (2\ theta_ {A} +\ theta_ {B} -3\ psi\ derecha) +F E M_ {A B}\\
2\ mathrm {EK}\ theta_ {B} -86.67
\ end {array}\]

\ [\ begin {array} {c}
M_ {B A} =\ frac {2\ mathrm {EI}} {L}\ left (\ theta_ {A} +2\ theta_ {B} -3\ psi\ derecha) +F E M_ {B A}\\
4\ mathrm {EK}\ theta_ {B} +86.67
\ end {array}\]

\ [\ begin {array} {c}
M_ {B C} =\ frac {2\ mathrm {EI}} {L}\ left (2\ theta_ {B} +\ theta_ {C} -3\ psi\ derecha) +F E M_ {B C}\\
4\ mathrm {EK}\ theta_ {B} -46.67
\ end {array}\]

\ [\ begin {array} {c}
M_ {C B} =\ frac {2\ mathrm {EI}} {L}\ left (\ theta_ {B} +2\ theta_ {C} -3\ psi\ derecha) +F E M_ {C B}\\
2\ mathrm {EK}\ theta_ {B} +46.67
\ end {array}\]

Ecuación de equilibrio articular.

La ecuación de equilibrio en la articulación\(B\) es la siguiente:

\ (\ begin {array} {l}
\ sum\ mathrm {M} _ {B} =\ mathrm {M} _ {B A} +\ mathrm {M} _ {B C} =0\\
4\ mathrm {EK}\ theta_ {B} +86.67+4\ mathrm {EK}\ theta_ {B} -46.67=0\
\ theta_ _ {B} =-\ frac {5} {\ mathrm {EK}}
\ end {array}\)

Momentos finales.

Sustituir\(\theta_{B}=-\frac{5}{\mathrm{EK}}\) en las ecuaciones 1, 2, 3 y 4 sugiere lo siguiente:

\ (\ begin {array} {l}
M_ {A B} =2\ mathrm {EK}\ left (-\ frac {5} {\ mathrm {EK}}\ derecha) -86.67=-96.67\ mathrm {kN}. \ mathrm {m}\\
M_ {B A} =4\ mathrm {EK}\ izquierda (-\ frac {5} {\ mathrm {EK}}\ derecha) +86.67=66.67\ mathrm {kN}. \ mathrm {m}\\
M_ {B C} =4\ mathrm {EK}\ izquierda (-\ frac {5} {\ mathrm {EK}}\ derecha) -46.67=-66.67\ mathrm {kN}. \ mathrm {m}\\
M_ {C B} =2\ mathrm {EK}\ izquierda (-\ frac {5} {\ mathrm {EK}}\ derecha) +46.67=36.67\ mathrm {kN}. \ mathrm {m}
\ fin {matriz}\)

Diagramas de fuerza de corte y momento de flexión.

Fuerza de corte y momento de flexión para segmento\(AB\).

Primero compute la reacción en soporte\(A\), de la siguiente manera:

\ (\ begin {array} {l}
\ curvearrowleft +\ sum M_ {B} =0: -4 A_ {y} +96.67+ (65) (4) (2) -66.67=0\\
A_ {y} =137.5\ mathrm {kN}
\ end {array}\)

Calcule la fuerza de corte, de la siguiente manera:

 

Cuando\(x = 0\),\(V=137.5 \mathrm{kN}\)

Cuando\(x = 4 \mathrm{m}\),\(V=-122.5 \mathrm{kN}\)

Encuentra el momento, de la siguiente manera:

\(M=137.5 x-\frac{(65)(x)^{2}}{2}-96.67\)

Cuando\(x = 0\),\(M=-96.67 \mathrm{kN} . \mathrm{m}\)

Cuando\(x = 4\) m,\(M=-66.67 \mathrm{kN} . \mathrm{m}\)

Fuerza de corte y momento de flexión para segmento\(AB\).

Primero determinar la reacción en\(B\), como sigue:

\ (\ begin {array} {l}
\ curvearrowleft +\ sum M_ {C} =0: -4 B_ {y} +66.67+ (35) (4) (2) -36.67=0\\
B_ {y} =77,5\ mathrm {kN}
\ end {array}\)

Calcule la fuerza de corte, de la siguiente manera:

 

Cuando\(x = 0\),\(V=77.5 \mathrm{kN}\).

Cuando\(x = 4\) m,\(V=-62.5 \mathrm{kN}\).

Encuentra el momento, de la siguiente manera:

\(M=77.5 x-\frac{(35)(x)^{2}}{2}-66.67\)

Cuando\(x = 0\),\(M=-66.67 \mathrm{kN} . \mathrm{m}\)

Cuando\(x = 4\) m,\(M=-36.67 \mathrm{kN} . \mathrm{m}\)

Diagramas de fuerza cortante y momento de flexión

Ejemplo 11.2

Mediante el método pendiente-deflexión, se determinan los momentos finales y las reacciones en los soportes de la viga que se muestran en la Figura 11.8a, y se dibujan los diagramas de fuerza de cizallamiento y momento de flexión. \(EI\)= constante.

\(Fig. 11.8\). Viga.

Solución

Rigidez relativa.

\(\left(K_{A B}\right):\left(K_{B C}\right)=\left(\frac{1}{12}\right):\left(\frac{3 I}{12}\right)=1: 3\)

Momentos de extremo fijo.

\ (\ begin {array} {l}
F E M_ {A B} =-\ frac {w\ mathrm {~L} ^ {2}} {20} =-\ frac {(4) (12) ^ {2}} {20} =-28.8\ mathrm {k}. \ mathrm {ft}\\
F E M_ {B A} =\ frac {w\ mathrm {~L} ^ {2}} {30} =\ frac {(4) (12) ^ {2}} {30} =19.2\ mathrm {k}. \ mathrm {ft}\\
F E M_ {B C} =-\ frac {\ mathrm {PL}} {8} =-\ frac {24\ times 12} {8} =-36\ mathrm {k}. \ mathrm {ft}\\
F E M_ {C B} =\ frac {\ mathrm {PL}} {8} =36\ mathrm {k}. \ mathrm {ft}
\ end {array}\)

Ecuaciones de deflexión en pendiente.

Observando que\(M_{C B}=\psi=0\), las ecuaciones para los momentos finales miembros pueden expresarse de la siguiente manera:\ [\ begin {aligned}
M_ {A B} & =( 2) (1)\ left (2\ theta_ {A} +\ theta_ {B} -3\ psi\ right) +F E M_ {A B}\\
&=2\ theta_ {B} -28.8
\ end {alineado}\]

\ [\ comenzar {alineado}
M_ {B A} & =( 2) (1)\ izquierda (\ theta_ {A} +2\ theta_ {B} -3\ psi\ derecha) +F E M_ {B A}\\
&=4\ theta_ {B} +19.2
\ end {alineado}\]

\ [\ comenzar {alineado}
M_ {B C} &=3 (3)\ izquierda (\ theta_ {B} -\ psi\ derecha) +F E M_ {B C} -\ frac {F E M_ {C B}} {2}\\
&=3 (3)\ theta_ {B} -36-\ frac {36} {2}\
&=9\ theta_ {B} -54
\ final {alineado}\]

Ecuación de equilibrio articular.

La ecuación de equilibrio en la articulación\(B\) es la siguiente:

\ (\ begin {array} {c}
\ suma M_ {B} =M_ {B A} +M_ {B C} =0\\
4\ theta_ {B} +19.2+9\ theta_ {B} -54=0\
\ theta_ {B} =\ frac {34.8} {13} =2.68
\ end {array}\)

Momentos finales.

Sustituir el valor calculado de\(\theta_{B}\) en las ecuaciones 1, 2 y 3 sugiere lo siguiente:

\ (\ begin {array} {l}
M_ {A B} =2 (2.68) -28.8=-23.4\ mathrm {k}. \ mathrm {ft}\\
M_ {B A} =4\ theta_ {B} +19.2=4 (2.68) +19.2=29.9\ mathrm {k}. \ mathrm {ft}\\
M_ {B C} =9\ theta_ {B} -54=9 (2.68) -54=-29.9\ mathrm {k.} \ mathrm {ft}\\
M_ {C B} =0
\ end {array}\)

Diagramas de fuerza cortante y momento de flexión

Fuerza de corte y momento de flexión para segmento\(AB\).

\ (\ begin {aligned}
\ curvearrowleft +&\ sum M_ {A} =0:12 B_ {y} +23.44-\ left (\ frac {1} {2}\ right) (12) (4)\ left (\ frac {1} {3}\ times 12\ right) -29.9=0\\
B_ {y} &=8.54\ mathrm {kips}\\
\ uparrow+\ suma F_ {y} =& 8.54+A_ {y} -\ izquierda (\ frac {1} {2}\ derecha) (12) (4) =0\\
A_ {y} &=15.46\ mathrm {kips}\\
V &=-8.54+\ izquierda (\ frac {1} {2}\ derecha) (x)\ izquierda (\ frac {x} {3}\ derecha) =-8.54+\ frac {x^ {2}} {6}
\ end {alineado}\)

Cuando\(x = 0\),\(V=-8.54 \mathrm{kips}\)

Cuando\(x = 12\) ft,\(V=15.46 \mathrm{kips}\)

\(M=8.54 x-\left(\frac{1}{2}\right)(x)\left(\frac{x}{3}\right)\left(\frac{1}{3} \times x\right)-29.9=8.54 x-\frac{(x)^{3}}{18}-29.9\)

Cuando\(x = 0\),\(M=-29.9 \mathrm{k} . \mathrm{ft}\)

Cuando\(x = 12\) ft,\(M=-23.4 \mathrm{k} . \mathrm{ft}\)

Fuerza de corte y momento de flexión para segmento\(BC\).

\ (\ begin {array} {l}
\ curvearrowleft +\ sum M_ {B} =0:12 C_ {y} +29.9- (24) (6) =0\\
C_ {y} =9.5\ mathrm {kips}\
\ uparrow+\ sum F_ {y} =0
\ end {array}\)

\ (\ begin {alineado}
&B_ {y} +9.5-24=0\\
&B_ {y} =14.5\ mathrm {kips}\\
&0<x<6\ mathrm {ft}\\
&V=14.5\ text {kips}\\
&M=14.5 x-29.9\
&\ text {Cuando} x=0, M=-29.9\ mathrm {k}. \ mathrm {ft}\\
&\ text {Cuando} x=6\ mathrm {ft}, M=57.10\ mathrm {k}. \ mathrm {ft}
\ final {alineado}\)

Ejemplo 11.3

Mediante el método pendiente-deflexión, se determinan los momentos finales de la viga que se muestra en la Figura 11.9a. Supongamos que el soporte\(B\) se asienta 1.5 in y dibuje la fuerza de corte y los diagramas de momento de flexión. El módulo de elasticidad y el momento de inercia del haz son\(29,000 \mathrm{ksi}\) y\(8000 \mathrm{in}^{4}\), respectivamente.

\(Fig. 11.9\). Viga.

Solución

Momentos de extremo fijo.

Los momentos de extremo fijo (FEM) usando la Tabla 11.1 se calculan de la siguiente manera:

\ (\ begin {array} {l}
F E M_ {A B} =-\ frac {w L^ {2}} {12} =-\ frac {5\ times 3^ {2}} {12} =-3.75\ mathrm {kN}. \ mathrm {m}\\
F E M_ {B A} =\ frac {w\ mathrm {~L} ^ {2}} {12} =3.75\ mathrm {kN}. \ mathrm {m}\\
F E M_ {B C} =-3.75\ mathrm {kN}. \ mathrm {m}\\
F E M_ {C B} =3.75\ mathrm {kN}. \ mathrm {m}\\
F E M_ {C D} =-\ frac {\ mathrm {Pab} ^ {2}} {L^ {2}} =\ frac {(20) (1.5) (1.5) ^ {2}} {3^ {2}} =-7.5\ mathrm {kN}. \ mathrm {m}\
F E M_ {D C} =\ frac {\ mathrm {P} a^ {2}\ mathrm {~b}} {L^ {2}} =\ frac {(20) (1.5) (1.5) ^ {2}} {3^ {2}} =7.5\ mathrm {kN}\ cdot\ mathrm {m}
\ fin matriz}\)

Ecuaciones de deflexión en pendiente.

At\(\theta_{A}=\theta_{D}=\psi=0\), las ecuaciones para los momentos finales miembros se expresan de la siguiente manera:\ [\ begin {aligned}
M_ {A B} &=\ frac {2\ mathrm {EI}} {L}\ left (2\ theta_ {A} +\ theta_ {B} -3\ psi\ right) -F E M_ {A B}\\\
=& 2\ mathrm {EK}\ theta_ {B} -3.75
\ final {alineado}\]

\ [\ begin {alineado}
M_ {B A} &=\ frac {2\ mathrm {EI}} {L}\ izquierda (\ theta_ {A} +2\ theta_ {B} -3\ psi\ derecha) +F E M_ {B A}\\
&=4\ mathrm {EK}\ theta_ {B} +3.75
\ end {alineado}\]

\ [\ begin {alineado}
M_ {B C} &=\ frac {2 E I} {L}\ izquierda (2\ theta_ {B} +\ theta_ {C} -3\ psi\ derecha) -F E M_ {B C}\\
=& 4\ mathrm {EK}\ theta_ {B} +2\ mathrm {EK}\ theta_ {C} -3.75
\ final {alineado}\]

\ [\ begin {alineado}
\ mathrm {M} _ {C B} =&\ frac {2\ mathrm {EI}} {L}\ izquierda (\ theta_ {B} +2\ theta_ {C} -3\ psi\ derecha) +\ mathrm {FEM} _ {C B}\\
=2\ mathrm {EK}\ theta_ {B} +4\ mathrm rm {EK}\ theta_ {C} +3.75 &
\ end {alineado}\]

\ [\ begin {alineado}
\ mathrm {M} _ {C D} =\ frac {2\ mathrm {EI}} {L}\ izquierda (2\ theta_ {C} +\ theta_ {D} -3\ psi\ derecha) -\ mathrm {FEM} _ {C D}\\
=4\ mathrm {EK}\ theta_ {c} -7.5
\ fin {alineado}\]

\ [\ begin {alineado}
\ mathrm {M} _ _ {D C} =\ frac {2\ mathrm {EI}} {L}\ izquierda (\ theta_ {C} +2\ theta_ {D} -3\ psi\ derecha) +\ mathrm {FEM} _ {D C}\\
=2\ mathrm {EK}\ theta_ {C} +7.5
\ final {alineado}\]

Ecuación de equilibrio articular.

La ecuación de equilibrio en la articulación\(B\) es la siguiente:\ [\ begin {array} {l}
\ qquad\ suma M_ {B} =M_ {B A} +M_ {B C} =0\\
4 E K\ theta_ {B} +3.75+4 E K\ theta_ {B} +2 E K\ theta_ {C} -3.75=0\\
8 E K\ theta_ {B} +2 E K\ theta_ {C} =0
\ final {matriz}\]

\ [\ begin {array} {l}
\ suma M_ {C} =M_ {C B} +M_ {C D} =0\\
2 E K\ theta_ {B} +4 E K\ theta_ {C} +3.75+4 E K\ theta_ {C} -7.5=0\\
2 E K\ theta_ {B} +8 E K\ theta_ {C} -3.75=0
\ end {array}\]

Resolver las ecuaciones 7 y 8 simultáneamente sugiere lo siguiente:

\(\theta_{B}=-\frac{0.125}{\mathrm{EK}} \text { and } \theta_{C}=\frac{0.5}{\mathrm{EK}}\)

Momentos finales.

Sustituir los valores obtenidos de\(\theta_{B}\) y\(\theta_{C}\) en las ecuaciones de pendiente-deflexión sugiere los siguientes momentos finales:

\ (\ begin {array} {l}
M_ {A B} =2 E K\ izquierda (-\ frac {0.125} {\ mathrm {EK}}\ derecha) -3.75=-4.00\ mathrm {kN}. \ mathrm {m}\\
M_ {B A} =4 E K\ izquierda (-\ frac {0.125} {\ mathrm {EK}}\ derecha) +3.75=3.25\ mathrm {kN}. \ mathrm {m}\\
M_ {B C} =4\ mathrm {EK}\ izquierda (\ frac {0.125} {\ mathrm {EK}}\ derecha) +2 (0.5) -3.75=-3.25\ mathrm {kN}. \ mathrm {m}\\
M_ {C B} =2\ mathrm {EK}\ izquierda (-\ frac {0.125} {\ mathrm {EK}}\ derecha) +4 (0.5) +3.75=5.50\ mathrm {kN}. \ mathrm {m}\\
M_ {C D} =4\ mathrm {EK}\ izquierda (-\ frac {0.5} {\ mathrm {EK}}\ derecha) -7.5=-5.50\ mathrm {kN}. \ mathrm {m}\\
M_ {D C} =2\ mathrm {EK}\ izquierda (-\ frac {0.5} {\ mathrm {EK}}\ derecha) +7.5=8.5\ mathrm {kN}. \ mathrm {m}
\ fin {matriz}\)

Ejemplo 11.4

Utilizando el método pendiente-deflexión, determinar los momentos finales del miembro de la viga de la sección transversal rectangular mostrada en la Figura 11.10a. Supongamos que el soporte\(B\) asienta 2 cm. El módulo de elasticidad y el momento de inercia del haz son\(E=210,000 \mathrm{~N} / \mathrm{mm}^{2}\) y\(4.8 \times 10^{4} \mathrm{~mm}^{4}\), respectivamente.

\(Fig. 11.10\). Sección transversal rectangular de la viga.

Solución

Los momentos de extremo fijo (FEM) usando la Tabla 11.1 se calculan de la siguiente manera:

\ (\ begin {array} {l}
F E M_ {A B} =-\ frac {P a b^ {2}} {L^ {2}} =-\ frac {(250) (2) (4) ^ {2}} {6^ {2}} =-222.22\ mathrm {kN}. \ mathrm {m}\\
F E M_ {B A} =\ frac {P a^ {2} b} {L^ {2}} =\ frac {(250) (2) ^ {2} (4)} {6^ {2}} =111.1\ mathrm {kN}. \ mathrm {m}\\
F E M_ {B C} =-\ frac {P L} {8} =-\ frac {(120) (6)} {8} =-90\ mathrm {kN}. \ mathrm {m}\\
F E M_ {C B} =\ frac {P L} {8} =\ frac {(120) (6)} {8} =90\ mathrm {kN}. \ mathrm {m}
\ fin {matriz}\)

Ecuaciones de deflexión en pendiente.

As\(\theta_{C}=0\), las ecuaciones para los momentos finales miembros se expresan de la siguiente manera:\ [\ begin {aligned}
M_ {B A} &=3 E K\ left (\ theta_ {B} -\ Psi\ right) +F E M_ {B A} -\ frac {F E M_ {A B}} {2}\\
&=3 E K\ left (\ theta_ {B} -\ fr{ 0.02} {6}\ derecha) +111.1-\ frac {(-222.2)} {2}\\
&=3 E K\ theta_ {B} -0.01 E K+222.2
\ final {alineado}\]

\ [\ comenzar {alineado}
M_ {B C} &=2 E K\ izquierda (2\ theta_ {B} +\ theta_ {C} -3\ psi\ derecha) +F E M_ {B C}\\
&=4 E K\ theta_ {B} +2 E K\ izquierda (-3\ veces\ frac {(-0.02)} {6}\ derecha) 90\\
&=4 E K\ theta_ {B} +0.02 E K-90
\ final {alineado}\]

\ [\ comenzar {alineado}
M_ {C B} &=2 E K\ izquierda (\ theta_ {B} +2\ theta_ {C} -3\ psi\ derecha) +F E M_ {C B}\\
&=2 E K\ theta_ {B} +0.02 E K+90
\ final {alineado}\]

Ecuación de equilibrio articular.

La ecuación de equilibrio en la articulación\(B\) se escribe de la siguiente manera:\ [\ begin {array} {l}
\ qquad\ suma M_ {B} =M_ {B A} +M_ {B C} =0\\
3 E K\ theta_ {B} -0.01 E K+222.2+4 E K\ theta_ {B} +0.02 E K-90=0\\
7 E K\ theta_ _ {B} +0.01 E K+132.2=0
\ end {array}\]

Resolver la ecuación 4 para\(\theta_{B}\) sugiere lo siguiente:

\ (\ begin {array} {l}
\ theta_ {B} =-0.0014-\ frac {18.89} {E K} =-0.0014-\ frac {18.89} {210\ times 10^ {9} K}\\
E K=210\ times 10^ {9}\ times\ frac {4.8\ times 10^ {4}} {\ left (10^ {12}\ derecha) (6)} =1680\\
\ theta_ {B} =-0.0014-\ frac {18.89} {1680} =-0.0126\ mathrm {rad}
\ end { matriz}\)

Momentos finales.

Sustituir el valor obtenido de\(\theta_{B}\) en las ecuaciones 1, 2 y 3 sugiere los siguientes momentos finales:

\ (\ begin {array} {l}
M_ {A B} =0\\
\ qquad M_ {B A} =141.9\ mathrm {kN}\ cdot\ mathrm {m}\\
M_ {B C} =4 E K\ izquierda (\ frac {0.125} {E K}\ derecha) +2 (0.5) -3.75=-141.07\ mathrm {N}. \ mathrm {m}\\
M_ {C B} =2 E K\ izquierda (-\ frac {0.125} {E K}\ derecha) +4 (0.5) +3.75=81.26\ mathrm {kN}. \ mathrm {m}
\ fin {matriz}\)

Ejemplo 11.5

Mediante el método pendiente-deflexión, se determinan los momentos finales del miembro y las reacciones en los soportes del marco mostrado en la Figura 11.11a. \(EI =\)constante.

\(Fig. 11.11\). Marco.

Solución

Momentos de extremo fijo.

Los momentos de extremo fijo (FEM) usando la Tabla 11.1 se calculan de la siguiente manera:

\ (\ begin {array} {l}
F E M_ {A B} =-\ frac {w\ mathrm {~L} ^ {2}} {12} =-\ frac {2\ times 10^ {2}} {12} =-16.67\ mathrm {k}. \ mathrm {ft}\\
F E M_ {B A} =\ frac {w L^ {2}} {12} =16.67\ mathrm {k}. \ mathrm {ft}\\
F E M_ {B C} =-\ frac {P L} {8} =-\ frac {20\ veces 6} {8} =-15\\
F E M_ {C B} =\ frac {P L} {8} =\ frac {20\ veces 6} {8} =15
\ final {array}\)

Ecuaciones de deflexión en pendiente.

\(\theta_{A}=\theta_{C}=0\)Debido a la fijedad en ambos extremos y\(\psi_{A B}=\psi_{B C}=0\) dado que no se produce ningún asentamiento, las ecuaciones para los momentos finales del miembro se expresan de la siguiente manera:\ [\ begin {aligned}
M_ {A B} &=2 E K\ left (2\ theta_ {A} +\ theta_ {B} -3\ psi\ right) +F E M_ {A B}\\
=2 E K\ theta_ {B} -16.67 y
\ end {alineado}\]

\ [\ comenzar {alineado}
M_ {B A} &=2 E K\ izquierda (\ theta_ {A} +2\ theta_ {B} -3\ psi\ derecha) +F E M_ {B A}\\
=4 E K\ theta_ {B} +16.67 &
\ end {alineado}\]

\ [\ comenzar {alineado}
& M_ {B C} =2 E K\ izquierda (2\ theta_ {B} +\ theta_ {C} -3\ psi\ derecha) +F E M_ {B C}\\
=4 E K\ theta_ {B} -15 &
\ end {alineado}\]

\ [\ comenzar {alineado}
M_ {C B} &=\ frac {2 E 1} {L}\ izquierda (\ theta_ {B} +2\ theta_ {C} -3\ psi\ derecha) +F E M_ {C B}\\
=2 E K\ theta_ {B} +15 &
\ final {alineado}\]

Ecuación de equilibrio articular.

La ecuación de equilibrio en la articulación\(B\) es la siguiente:

\ (\ begin {array} {l}
\ suma M_ {B} =M_ {B A} +M_ {B C} =0\\
4 E K\ theta_ {B} +16.67+4 E K\ theta_ {B} -15=0\
\ qquad E K\ theta_ {B} =-\ frac {1.67} {8} =-0.209
\ fin {matriz}\)

Momentos finales.

Sustituir\(E K \theta_{B}=-0.209\) en las ecuaciones 1, 2, 3 y 4 sugiere lo siguiente:

\ (\ begin {array} {l}
M_ {A B} =-17.09\ mathrm {k}. \ mathrm {ft}\\
M_ {B A} =15.83\ mathrm {k.ft}\\
M_ {B C} =-15.83\ mathrm {k.ft}\\
M_ {C B} =14.58\ mathrm {k.ft}
\ end {array}\)

Reacciones en soportes.

Para determinar\(A_{x}\), tómate el momento aproximadamente\(B\) en la Figura 11.11c, de la siguiente manera:

\ (\ begin {array} {l}
+\ curvearrowleft\ Sigma M_ {B} =0:17.09+ (2) (10) (5) -15.83-10 A_ {x} =0\\
A_ {x} =10.13\ mathrm {k}
\ end {array}\)

Para determinar\(A_{y}\), tómate el momento aproximadamente\(C\) en la Figura 11.11b, de la siguiente manera:

\ (\ begin {array} {l}
+\ curvearrowleft\ sum M_ {C} =0; 17.09-10.13\ times 10+ (2) (10) (5) +20\ times 3-14.58-6 A_ {y} =0\\
A_ {y} =10.20\ mathrm {k}
\ end {array}\)

Para determinar\(C_{y}\) en la Figura 11.11b, considere la suma de fuerzas en dirección vertical, de la siguiente manera:

\ (\ begin {array} {l}
+\ uparrow\ suma F_ {y} =0\\
10.20-20+C_ {y} =0\\
C_ {y} =9.80\ mathrm {k}
\ end {array}\)

Para determinar\(C_{x}\) en la Figura 11.11b, considere la suma de fuerzas en dirección horizontal, de la siguiente manera:

\ (\ begin {array} {l}
+\ fila derecha\ suma F_ {x} =0\\
2\ times 10-10.13-C_ {x} =0\\
C_ {x} =9.87\ mathrm {k}
\ end {array}\)

Ejemplo 11.6

Utilizando el método pendiente-deflexión, determine los momentos finales del miembro del marco que se muestra en la Figura 11.12a.

\(Fig. 11.12\). Marco.

Solución

Momentos de extremo fijo.

Los momentos de extremo fijo (FEM) usando la Tabla 11.1 se calculan de la siguiente manera:

\ (\ begin {array} {l}
F E M_ {A B} =-\ frac {w L^ {2}} {12} =-\ frac {10\ times 6^ {2}} {12} =-30\ mathrm {kN}. \ mathrm {m}\\
F E M_ {B A} =\ frac {w L^ {2}} {12} =30\ mathrm {kN}. \ mathrm {m}\\
F E M_ {B C} =-\ frac {10\ times 4^ {2}} {12} =-10.33\ mathrm {kN}. \ mathrm {m}\\
\ mathrm {FEM} _ {C B} =10.33\ mathrm {kN}. \ mathrm {m}\\
F E M_ {D B} =-\ frac {P L} {8} =-\ frac {20\ times 8} {8} =-20\ mathrm {kN}. \ mathrm {m}\\
F E M_ {B D} =\ frac {P L} {8} =\ frac {20\ times 8} {8} =20\ mathrm {kN}. \ mathrm {m}
\ fin {matriz}\)

Ecuaciones de deflexión en pendiente.

Como\(\theta_{A}=\theta_{C}=0\) debido a la fijedad en ambos extremos y\(\psi_{A B}=\psi_{B C}=0\) dado que no se produce ningún asentamiento, las ecuaciones para los momentos finales miembros se pueden expresar de la siguiente manera:\ [\ begin {aligned}
M_ {B A} &=3 E K\ left (\ theta_ {B} -\ psi\ right) +F E M_ {B A} -\ frac {F E M_ {A B}} {2}\\
&=3 E K\ theta_ {B} +30-\ frac {(-30)} {2} =3 E K\ theta_ {B} +45
\ final {alineado}\]

\ [\ comenzar {alineado}
& M_ {B C} =2 E K\ izquierda (2\ theta_ {B} +\ theta_ {C} -3\ psi\ derecha) +F E M_ {B C}\\
=4 E K\ theta_ {B} -10.33 &
\ end {alineado}\]

\ [\ comenzar {alineado}
M_ {C B} &=2 E K\ izquierda (\ theta_ {B} +2\ theta_ {C} -3\ psi\ derecha) +F E M_ {C B}\\
=2 E K\ theta_ {B} +10.33 &
\ end {alineado}\]

\ [\ comenzar {alineado}
M_ {D B} &=2 E K\ izquierda (2\ theta_ {D} +\ theta_ {B} -3\ psi\ derecha) +F E M_ {D B}\\
=2 E K\ theta_ {B} -20 &
\ end {alineado}\]

\ [\ comenzar {alineado}
M_ {B D} &=2 E K\ izquierda (2\ theta_ {B} +\ theta_ {D} -3\ psi\ derecha) +F E M_ {B D}\\
=4 E K\ theta_ {B} +20 &
\ end {alineado}\]

Ecuación de equilibrio articular.

La ecuación de equilibrio en la articulación\(B\) es la siguiente:

\ (\ begin {array} {l}
\ suma M_ {B} =M_ {B A} +M_ {B C} +M_ {B D} =0\\
3 E K\ theta_ {B} +45+4 E K\ theta_ {B} -10.33+4 E K\ theta_ {B} +20=0\
E K\ theta_ {B} =-4.97
\ end {array}\)

Momentos finales.

Sustituir\(\mathrm{EK} \theta_{B}=-4.97\) en las ecuaciones 1, 2, 3, 4 y 5 sugiere lo siguiente:

\ (\ begin {alineado}
M_ {A B} =0\\
M_ {B A} =30.09\ mathrm {kN}. \ mathrm {m}\\
M_ {B C} =-30.21\ mathrm {kN}. \ mathrm {m}\\
M_ {C B} =0.39\ mathrm {kN}. \ mathrm {m}\\
M_ {D B} =-29.94\ mathrm {kN}. \ mathrm {m}\\
M_ {B D} =0.12\ mathrm {kN}. \ mathrm {m}
\ final {alineado}\)

Ejemplo 11.7

Utilizando el método pendiente-deflexión, determine los momentos finales del miembro del marco que se muestra en la Figura 11.13a.

\(Fig. 11.13\). Marco.

Solución

Momentos de extremo fijo.

Los momentos de extremo fijo (FEM) usando la Tabla 11.1 se calculan de la siguiente manera:

\ (\ begin {array} {l}
F E M_ {A B} =-\ frac {w\ mathrm {~L} ^ {2}} {12} =-\ frac {10\ times 8^ {2}} {12} =-53.33\ mathrm {kN}. \ mathrm {m}\\
F E M_ {B A} =\ frac {w\ mathrm {~L} ^ {2}} {12} =53.33\ mathrm {kN}. \ mathrm {m}\\
F E M_ {B C} =\ mathrm {FEM} _ {B C} =0
\ final {matriz}\)

Ecuaciones de deflexión en pendiente.

As\(\theta_{A}=\psi_{B C}=0\) y\(\psi_{A B}=\frac{\Delta}{8}\) las ecuaciones para los momentos finales miembros se pueden expresar de la siguiente manera:\ [\ begin {aligned}
M_ {A B} &=2 E K\ left (2\ theta_ {A} +\ theta_ {B} -3\ psi\ right) +F E M_ {A B}\\
=& 2 E K\ left [\ theta_ {B} -3\ left (\ frac {-\ Delta} {8}\ derecha)\ derecha] -53.33\\
=& 2 E K\ theta_ {B} +0.75 E K\ Delta-53.33
\ final {alineado}\]

\ [\ begin {alineado}
\ mathrm {M} _ {\ mathrm {BA}} &=2\ mathrm {EK}\ left (\ theta_ {\ mathrm {A}} +2\ theta_ {\ mathrm {B}} -3\ izquierda (\ frac {-\ Delta} {8}\ derecha)\ derecha) +\ mathrm {FEM} _ {B A}\\
=& 2 E K\ izquierda [2\ theta_ {B} -3\ izquierda (\ frac {-\ Delta} {8}\ derecha)\ derecha] +53.33\\
=& 4 E K\ theta _ {B} +0,75 E K\ Delta+53.33
\ final {alineado}\]

\ [\ begin {alineado}
M_ {B C} &=3 E K\ izquierda (\ theta_ {B} -\ psi\ derecha) +\ mathrm {FEM} _ {B C} -\ frac {\ mathrm {FEM} _ {C B}} {2}\\
&=3 E K\ theta_ {B}
\ end {alineado}\]

Ecuación de equilibrio articular.

\ [\ begin {array} {l}
\ suma M_ {B} =M_ {B A} +M_ {B C} =0\\
4 E K\ theta_ {B} +0.75 E K\ Delta+53.33+3\ mathrm {EK}\ theta_ {B} =0\\
7 E K\ theta_ {B} +0.75 E K\ Delta=-53. .33
\ fin {array}\]

El equilibrio de las fuerzas horizontales en la Figura 11.13b sugiere lo siguiente:\ [\ begin {array} {l}
+\ rightarrow\ sum F_ {x} =0\\
(10) (8) -A_ {x} =0
\ end {array}\]

La Figura 11.13c sugiere lo siguiente:\[A_{x}=\frac{M_{A B}+M_{B A}+(10)(8)(4)}{8}\]

Sustituir\(A_{x}\) de la ecuación 6 a la ecuación 5 sugiere lo siguiente:\ [\ begin {array} {l}
80-\ frac {M_ {A B} +M_ {B A} +320} {8} =0\\
640-320=M_ {A B} +M_ {B A}
\ end {array}\]

Sustituyendo\(M_{AB}\) y\(M_{BA}\) de las ecuaciones 1 y 2 a la ecuación 7 sugiere lo siguiente:\ [\ begin {array} {l}
2 E K\ theta_ {B} +0.75 E K\ Delta-53.33+4 E K\ theta_ {B} +0.75 E K\ Delta+53.33=320\
6 E K\ theta_ {B} +1.5 E K\ Delta=320
\ end {matriz}\]

Resolver las ecuaciones 4 y 8 simultáneamente sugiere lo siguiente:

\(E K \theta_{B}=-53.33\)y\(E K \Delta=426.66\)

Momentos finales del miembro final.

Poner los valores obtenidos de\(E K \theta_{B}\) y\(E K \Delta\) en las ecuaciones 1, 2 y 3 para los momentos finales de los miembros sugiere lo siguiente:

\ (\ begin {alineado}
\ mathrm {M} _ {A B} =2\ mathrm {EK}\ theta_ {B} +0.75\ mathrm {EK}\ Delta-53.33=160\ mathrm {kN}. \ mathrm {m}\\
\ mathrm {M} _ {B A} =4\ mathrm {EK}\ theta_ {B} +0.75\ mathrm {EK}\ Delta+53.33=160\ mathrm {kN}. \ mathrm {m}\\
\ mathrm {M} _ {B C} =3\ mathrm {EK}\ theta_ {B} =-160\ mathrm {kN}. \ mathrm {m}\\
\ mathrm {M} _ {C B} =0
\ final {alineado}\)

Ejemplo 11.8

Utilizando el método pendiente-deflexión, determinar los momentos finales del miembro de la viga de la sección transversal rectangular mostrada en la Figura 11.14a.

\(Fig. 11.14\). Viga.

Solución

Momentos de extremo fijo.

Los momentos de extremo fijo (FEM) usando la Tabla 11.1 se calculan de la siguiente manera:

\ (\ begin {array} {l}
F E M_ {A B} =-\ frac {P L} {8} =-\ frac {40\ times 8} {8} =-40.0\ mathrm {kN}. \ mathrm {m}\\
F E M_ {B A} =\ frac {P L} {8} =40.0\ mathrm {kN}. \ mathrm {m}\\
F E M_ {B C} =-\ frac {P a b^ {2}} {L^ {2}} =-\ frac {(30) (2) (4) ^ {2}} {6^ {2}} =-26.67\ mathrm {kN}. \ mathrm {m}\\
F E M_ {C B} =\ frac {P a^ {2} b} {L^ {2}} =\ frac {(30) (2) ^ {2} (4)} {6^ {2}} =13.33\ mathrm {kN}. \ mathrm {m}
\ fin {matriz}\)

Ecuaciones de deflexión en pendiente.

Como\(\theta_{A}=\theta_{D}=0\) y\(\psi_{A B}=\frac{\Delta}{8}\), las ecuaciones para los momentos finales miembros se pueden expresar de la siguiente manera:\ [\ begin {aligned}
M_ {A B} &=2 E K\ left (2\ theta_ {A} +\ theta_ {B} -3\ psi\ right) +F E M_ {A B}\\
&=2 E K\ left [\ theta_ {B} -3\ left (\ frac {-\ Delta} {8}\ derecha)\ derecha] -40\\
&= 2 E K\ theta_ {B} +0.75 E K\ Delta-40
\ final {alineado}\]

\ [\ comenzar {alineado}
M_ {B A} &=2 E K\ izquierda (\ theta_ {A} +2\ theta_ {B} -3\ izquierda (\ frac {-\ Delta} {8}\ derecha)\ derecha) +F E M_ {B A}\\
&=2 E K\ izquierda [2\ theta_ {B} -3\ izquierda (\ frac {-\ Delta} {8}\ derecha)\ derecha] +40\\
&=4 E K\ theta_ {B} +0.75 E K\ Delta+40
\ final {alineado}\]

\ [\ comenzar {alineado}
M_ {B C} &=2 E K\ izquierda (2\ theta_ {B} +\ theta_ {C} -3\ psi\ derecha) +F E M_ {B C}\\
&=4 E K\ theta_ {B} +2 E K\ theta_ {C} -26.67
\ fin {alineado}\]

\ [\ begin {alineado}
\ mathrm {M} _ {C B} =& 2 E K\ izquierda (\ theta_ {B} +2\ theta_ {C}\ derecha) +F E M_ {C B}\\
=& 2 E K\ theta_ {B} +4 E K\ theta_ {C} +13.33
\ fin {alineado}\]

\ [\ comenzar {alineado}
M_ {C D} &=2 E K\ izquierda (2\ theta_ {C} +\ theta_ {D} -3\ psi\ derecha) +F E M_ {C D}\\
&=4 E K\ theta_ {C} +0.75 E K\ Delta
\ final {alineado}\]

\ [\ comenzar {alineado}
M_ {D C} &=2 E K\ izquierda (\ theta_ {C} +2\ theta_ {D} -3\ psi\ derecha) +F E M_ {D C}\\
&=2 E K\ theta_ {C} +0.75 E K\ Delta
\ final {alineado}\]

Ecuación de equilibrio articular. \ [\ begin {array} {l}
\ suma M_ {B} =M_ {B A} +M_ {B C} =0\\
4 E K\ theta_ {B} +0.75 E K\ Delta+40+4 E K\ theta_ {B} +2 E K\ theta_ {C} -26.67=0\\
8 E K\ theta_ {B} +2 E K\ theta_ {C} +0.75 E K\ Delta=-13.33
\ fin {matriz}\]

\ [\ begin {array} {l}
\ suma M_ {C} =M_ {C B} +M_ {C D} =0\\
2 E K\ theta_ {B} +4 E K\ theta_ {C} +13.33+4 E K\ theta_ {C} +0.75 E K\ Delta=0\\
2 E K\ theta_ {B} 8 E K\ theta_ {C} +0.75 E K\ Delta=-13.33
\ fin {matriz}\]

\ [\ begin {array} {l}
\ suma F_ {x} =0\\
40-A_ {x} -D_ {x} =0
\ end {array}\]

Sustituyendo\(A_{x}=\frac{M_{A B}+M_{B A}+(40 \times 4)}{8}\) and \(D_{x}=\frac{M_{C D}+M_{D C}}{8}\) into the previous equation suggests the following: \[\begin{array}{l}
40-\frac{M_{A B}+M_{B A}+(40 \times 4)}{8}-\frac{M_{C D}+M_{D C}}{8}=0 \\
\frac{M_{A B}+M_{B A}+(40 \times 4)}{8}+\frac{M_{C D}+M_{D C}}{8}=320 \\
M_{A B}+M_{B A}+(40 \times 4)+M_{C D}+M_{D C}=320
\end{array}\]

Sustituir las expresiones de\(M_{AB}\),\(M_{BA}\),\(M_{CD}\) y\(M_{DC}\) de las ecuaciones 1, 2, 5 y 6 en e sugiere lo siguiente:\ [\ begin {array} {l}
2 E K\ theta_ {B} +0.75 E K\ Delta-40+4 E K\ theta_ {B} +0.75 E K\ Delta+40+160+4 E K\ theta_ {C} +0.75 E K\ Delta+\\
2 E K \ theta_ {C} +0.75 E K\ Delta=320\\
6 E K\ theta_ {B} +6 E K\ theta_ {C} +3 E K\ Delta=160
\ final {matriz}\]

Resolver las ecuaciones 7, 8 y 11 simultáneamente sugiere lo siguiente:

\ (\ begin {array} {l}
E K\ theta_ {B} =-7.62\\
E K\ theta_ {C} =-7.62\\
E K\ Delta=83.81
\ end {array}\)

Momentos finales del miembro final.

Sustituir los valores obtenidos de\(E K \theta_{B}\),\(E K \theta_{C}\) y\(E K \Delta\) en ecuaciones de momento final de miembro sugiere lo siguiente:

\ (\ begin {array} {l}
M_ {A B} =2 E K\ theta_ {B} +0.75 E K\ Delta-40=7.62\\
M_ {B A} =4 E K\ theta_ {B} +0.75 E K\ Delta+40=72.39\\
M_ {B C} =4 E K\ theta_ {B} +2 K\ theta_ {C} -26.67=-72.39\\
M_ {C B} =2 E K\ theta_ {B} +4 E K\ theta_ {C} +13.33=-32.39\\
M_ {C D} =4 E K\ theta_ {C} +0.75 E K\ Delta=32.39\\
M_ {D C} =2 E K\ theta_ {C} +0.75 E K\ Delta=47.62
\ end {array}\)

\(Table 11.1\). Momentos de extremo fijo.

Tipo de carga	(FEM) AB	(FEM) BA
	\(\frac{Pab^2}{L^2}\)	\(\frac{Pa^2b}{L^2}\)
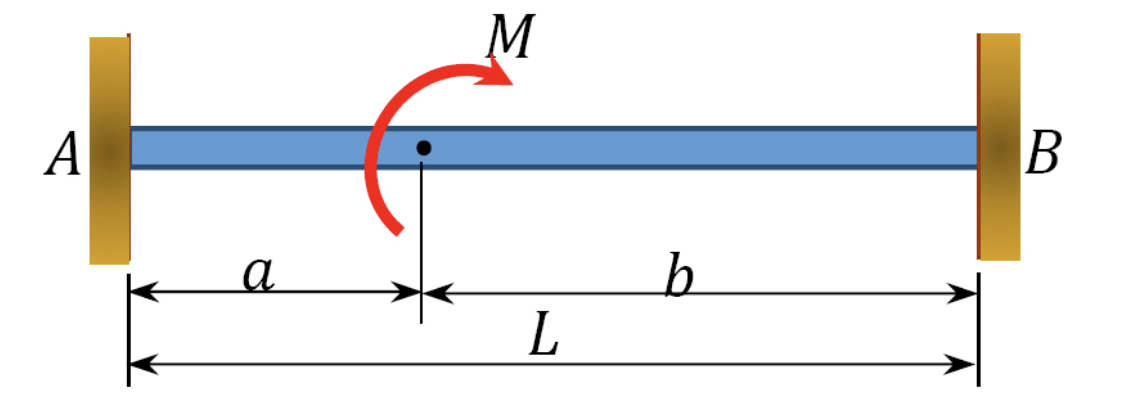	\(b(2a-b)\frac{M}{L^2}\)	\(a(2b-a)\frac{M}{L^2}\)
	\(\frac{wL^2}{12}\left(6-8\frac{a}{L}+3\frac{a^2}{L^2}\right)\)	\(\frac{wL^2}{12}\left(4-3\frac{a}{L}\right)\)
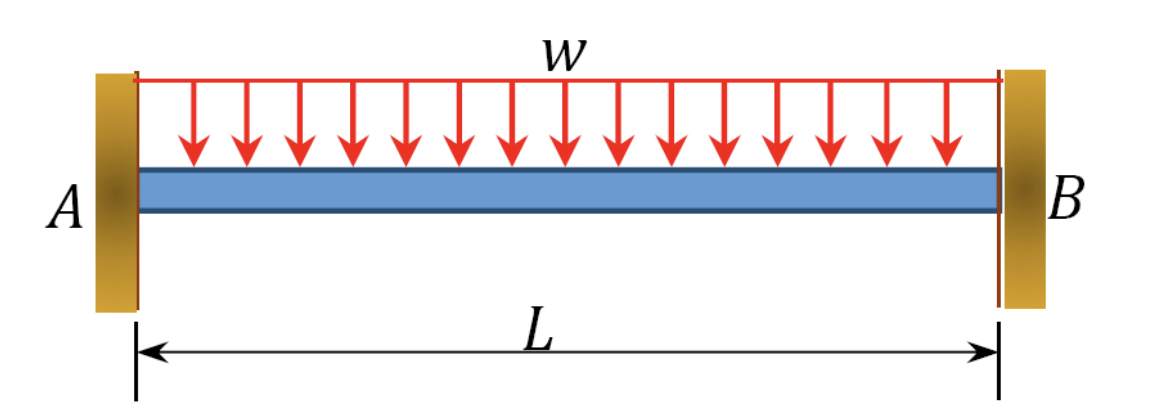	\(\frac{wL^2}{12}\)	\(\frac{wL^2}{12}\)
	\(\frac{wa^3}{60L}\left(5-3\frac{a}{L}\right)\)	\(\frac{wa^2}{60}\left(16-10\frac{a}{L}+3\frac{a^2}{L^2}\right)\)
	\(\frac{wL^2}{30}\)	\(\frac{wL^2}{20}\)
	\(\frac{5wL^2}{96}\)	\(\frac{5wL^2}{96}\)

Resumen del Capítulo

Método de análisis de pendiente-deflexión de estructuras indeterminadas: Las incógnitas en el método de análisis pendiente-deflexión son las rotaciones y los desplazamientos relativos. Las ecuaciones de deflexión de pendiente para los momentos de fin de miembro y la ecuación de equilibrio en cada articulación que es libre de rotar se escriben en términos de las rotaciones y desplazamientos relativos, y se resuelven simultáneamente para determinar las incógnitas. Cuando se determinan las rotaciones desconocidas y los desplazamientos relativos, se vuelven a colocar en ecuaciones de momento final de miembros para determinar la magnitud de los momentos. Después de la determinación de los momentos finales, la estructura se vuelve determinada. Los procedimientos detallados para el análisis por el método pendiente-deflexión para vigas y marcos se presentan en las secciones 11.5 y 11.6. En situaciones donde hay varias incógnitas, el análisis utilizando este método puede ser muy engorroso, de ahí la disponibilidad de software que pueda realizar el análisis.

Ecuaciones de deflexión en pendiente para momentos mnd:

\ (\ begin {array} {l}
M_ {A B} =2 E K\ izquierda (2\ theta_ {A} +\ theta_ {B} -3\ psi\ derecha) +M_ {A B} ^ {F}\\
M_ {B A} =0=2 E K\ izquierda (\ theta_ {A} +2\ theta_ {B} -3\ psi\ derecha) +M_ {B A} ^ {F}
\ end {array}\)

Ecuación de pendiente y deflexión modificada cuando el extremo lejano está soportado por un rodillo o pasador:

\(M_{A B}=3 E K\left(\theta_{A}-\psi\right)+\left(M_{A B}^{F}-\frac{M_{B A}^{F}}{2}\right)\)

Problemas de práctica

11.1 Usando el método pendiente-deflexión, compute el momento final de los miembros de las vigas que se muestran en la Figura P11.1 a la Figura P11.5 y dibuje los diagramas de momento de flexión y fuerza de corte. \(EI =\)constante.

\(Fig. P11.1\). Viga.

\(Fig. P11.2\). Viga.

\(Fig. P11.3\). Viga.

\(Fig. P11.4\). Viga.

\(Fig. P11.5\). Viga.

11.2 Usando el método pendiente-deflexión, compute los momentos finales de los miembros de las vigas que se muestran en la Figura P11.6. Supongamos que el soporte\(E\) se asienta por 50 mm. \(E=200 \mathrm{GPa}\)y\(I=600 \times 10^{6} \mathrm{~mm}^{4}\).

\(Fig. P11.6\). Viga.

11.3 Usando el método pendiente-deflexión, determinar los momentos finales de los miembros de los marcos no oscilantes mostrados en la Figura P11.7 a la Figura P11.10. Dibuje el momento de flexión y los diagramas de fuerza de corte.

\(Fig. P11.7\). Bastidor sin giro.

\(Fig. P11.8\). Bastidor no — Sway.

\(Fig. P11.9\). Bastidor no — Sway.

\(Fig. P11.10\). Bastidor no — Sway.

11.4 Mediante el método pendiente-deflexión, se determinan los momentos finales de los miembros de los bastidores oscilantes mostrados en la Figura P11.11 a la Figura P11.14. Dibuje el momento de flexión y los diagramas de fuerza de corte.

\(Fig. P11.11\). Bastidor de Sway.

\(Fig. P11.12\). Bastidor de Sway.

\(Fig. P11.13\). Bastidor de Sway.

\(Fig. P11.14\). Bastidor de Sway.