17.8: Apéndice 2 Problemas con las tareas
- Page ID
- 84007
Ejercicio\(\PageIndex{1}\)
Una forma está delimitada a la izquierda por el\(y\) eje -eje, en la parte inferior por el\(x\) eje -y a lo largo de su lado restante por la función\(y = - \dfrac{1}{2} x^2 + 8\). Determinar las\(y\) coordenadas\(x\) y del centroide de esta forma vía integración. (Sugerencia: para\(\bar{y}\), trabajar de arriba hacia abajo para facilitar las matemáticas.)
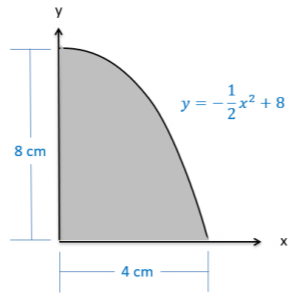.png)
- Solución:
-
\(\bar{x} = 1.5 \ cm, \, \bar{y} = 3.2 \ cm\)
Ejercicio\(\PageIndex{2}\)
Determinar las\(y\) coordenadas\(x\) y del centroide de la forma que se muestra a continuación mediante integración.
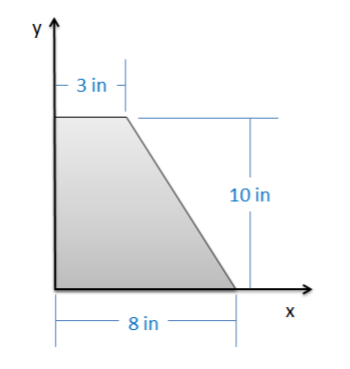.png)
- Solución:
-
\(\bar{x} = 2.94 \ in, \, \bar{y} = 4.24 \ in.\)
Ejercicio\(\PageIndex{3}\)
Un tanque de agua como se muestra a continuación toma la forma de un cono invertido y truncado. El diámetro de la base es de 4 pies, el diámetro de la parte superior es de 8 pies y la altura del tanque es de 4 pies. Mediante la integración, determine la altura del centro de masa del tanque lleno. (Supongamos que el tanque está lleno de agua y las paredes tienen una masa insignificante).
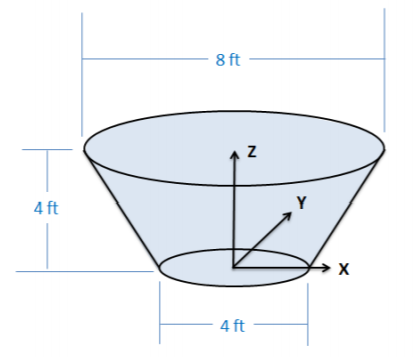.png)
- Solución:
-
\(z_c = 2.43 \ ft\)
Ejercicio\(\PageIndex{4}\)
Utilice el método de piezas compuestas para determinar el centroide de la forma que se muestra a continuación.
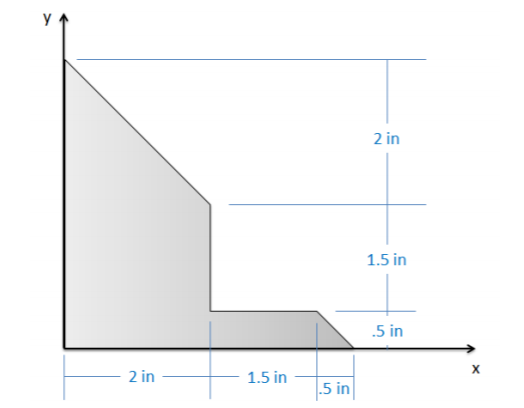.png)
- Solución:
-
\(x_c = 1.14 \ in, \, y_c = 1.39 \ in\)
Ejercicio\(\PageIndex{5}\)
Una plataforma flotante consiste en una pieza cuadrada de madera contrachapada que pesa 50 lbs con un grosor insignificante en la parte superior de un prisma rectangular de un material de espuma que pesa 100 lbs como se muestra a continuación. Con base en esta información, ¿cuál es la ubicación del centro de masa para la plataforma flotante?
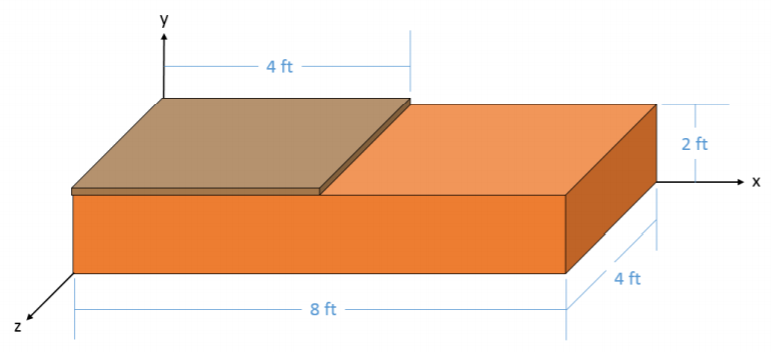.png)
- Solución:
-
\(x_c = 3.33 \ ft, \, y_c = 1.33 \ ft, \, z_c = 2 \ ft\)
Ejercicio\(\PageIndex{6}\)
Utilice el método de integración para encontrar los momentos de inercia para la forma que se muestra a continuación...
- Acerca del\(x\) eje -a través del centroide.
- Acerca del\(y\) eje -a través del centroide.
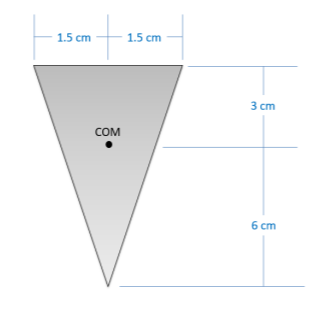.png)
- Solución:
-
\(I_{xx} = 6.075 * 10^{-7} \ m^4\)
\(I_{yy} = 5.0625 * 10^{-8} \ m^4\)
Ejercicio\(\PageIndex{7}\)
Utilice el método de integración para encontrar el momento polar de inercia para el semicírculo que se muestra a continuación sobre el punto O.
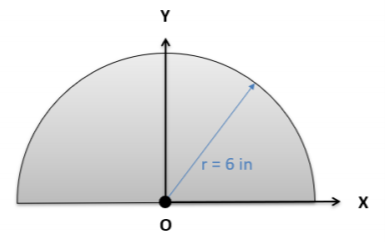.png)
- Solución:
-
\(J_{zz} = 1017.9 \ in^4\)
Ejercicio\(\PageIndex{8}\)
Una viga de plástico tiene una sección transversal cuadrada con recortes semicirculares en la parte superior e inferior como se muestra a continuación. ¿Cuál es el momento de inercia del área de la sección transversal de la viga sobre los\(y\) ejes\(x\) y a través del punto central?
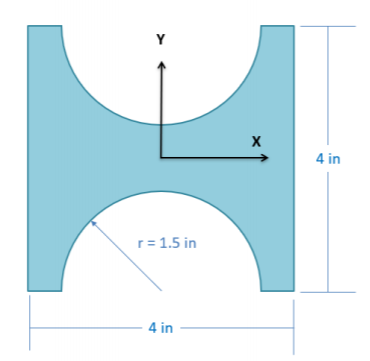.png)
- Solución:
-
\(I_{xx} = 7.08 \ in^4, \, I_{yy} = 17.36 \ in^4\)
Ejercicio\(\PageIndex{9}\)
Una pieza de acero en ángulo tiene una sección transversal que es de 1 cm de grosor y tiene una longitud de 6 cm en cada lado como se muestra a continuación. ¿Cuáles son los momentos de inercia\(x\) y del\(y\) área a través del centroide de la sección transversal?
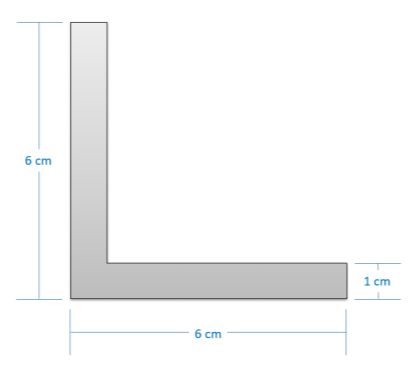.png)
- Solución:
-
\(I_{xx} = I_{yy} = 35.462 \ cm^4 = 3.546 * 10^{-7} \ m^4\)
Ejercicio\(\PageIndex{10}\)
El péndulo en un reloj antiguo consiste en un disco de latón con una masa de 0.25 kg y diámetro de 6 cm al final de una esbelta varilla de madera con una masa de 0.1 kg. Determinar el momento de inercia de masa del péndulo alrededor de la parte superior de la varilla.
.png)
- Solución:
-
\(I_{zz} = 0.02026 \ kg \ m^2\)
Ejercicio\(\PageIndex{11}\)
Un telescopio espacial se puede aproximar como un cilindro de 600 kg con un diámetro de 4 metros y una altura de 4 metros unido a dos paneles solares de 100 kg como se muestra a continuación. ¿Cuál es el momento de inercia de masa aproximado para el telescopio espacial alrededor del\(y\) eje mostrado?
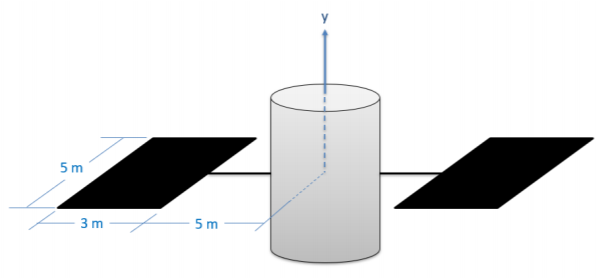.png)
- Solución:
-
\(I_{yy} = 10,216.7 \ kg \ m^2\)
Ejercicio\(\PageIndex{12}\)
Un volante tiene un peso original de 15 libras y un diámetro de 6 pulgadas. Para reducir el peso, se perforan cuatro orificios de dos pulgadas de diámetro en el volante, cada uno dejando media pulgada hacia el borde exterior como se muestra a continuación. ¿Cuál fue el momento original de la masa polar sobre el punto central? Asumiendo un espesor uniforme, ¿cuál es el nuevo momento de inercia de masa después de perforar los agujeros? (Sugerencia: los agujeros cuentan como masa negativa en los cálculos de momento de masa.)
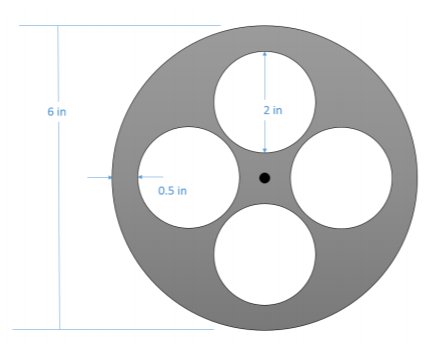.png)
- Solución:
-
\(J_{without holes} = 0.01456 \ slug \ ft^2\)
\(J_{with holes} = 0.01060 \ slug \ ft^2\)

