Inicio
Ingeniería
Ingeniería Mecánica
Mapa Mecánico (Moore et al.)
17: Apéndice 2 - Integrales de momento
17.7: Momentos de inercia a través de piezas compuestas y teorema de ejes paralelos

17.7: Momentos de inercia a través de piezas compuestas y teorema de ejes paralelos

Última actualización
Guardar como PDF

Page ID: 84027

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Como alternativa a la integración, los momentos de inercia tanto de área como de masa se pueden calcular a través del método de piezas compuestas, similar a lo que hicimos con los centroides. En este método descompondremos una forma compleja en partes simples, buscaremos los momentos de inercia para estas partes en una tabla, ajustaremos los momentos de inercia para la posición, y finalmente sumaremos los valores ajustados para encontrar el momento general de inercia. Este método se conoce como el método de piezas compuestas.

Una parte clave de este proceso que no estuvo presente en los cálculos del centroide es el ajuste por posición. Como se discutió en las páginas anteriores, los momentos de inercia de área y masa dependen del eje de rotación elegido. Los momentos de inercia para las partes del cuerpo solo se pueden agregar cuando se toman alrededor del mismo eje. Sin embargo, los momentos de inercia en la tabla generalmente se enumeran en relación con el centroide de esa forma. Debido a que cada parte tiene su propia coordenada centroide individual, no podemos simplemente sumar estos números. Usaremos algo llamado Teorema del Eje Paralelo para ajustar los momentos de inercia para que todos se tomen alrededor de algún eje o punto estándar. Una vez ajustados los momentos de inercia con el Teorema del Eje Paralelo, entonces podemos sumarlos usando el método de piezas compuestas.

Teorema del Eje Paralelo

Cuando calculamos los momentos de inercia de área y masa vía integración, una de las primeras cosas que tuvimos que hacer fue seleccionar un punto o eje sobre el que íbamos a tomar el momento de inercia. Luego medimos todas las distancias desde ese punto o eje, donde las distancias eran los brazos de momento en nuestras integrales de momento. Debido a que el centroide de una forma es el centro geométrico de un área o volumen, la distancia promedio desde el centroide a cualquier punto de un cuerpo es mínima. Si elegimos un punto o eje diferente para tomar el momento de inercia aproximadamente, entonces en promedio todas las distancias en nuestro momento integral serán un poco mayores. Específicamente, cuanto más nos movemos del centroide, mayores serán las distancias promedio.

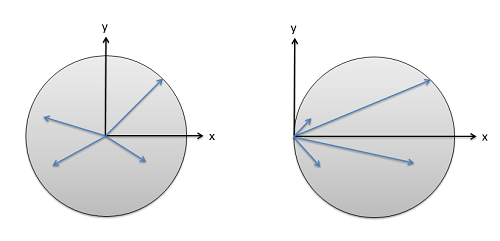
Cuando se calcula el momento de inercia de un disco sobre su centroide, el brazo de momento utilizado en esta integración puede variar de 0 a R (donde la R es el radio general del disco). Cuando el momento de inercia del disco se calcula alrededor de un punto en un borde, el brazo de momento utilizado en esta integración puede variar de 0 a 2R. — Figura\(\PageIndex{1}\): Las distancias utilizadas en nuestras integrales de momento dependen del punto o eje elegido. Estas distancias estarán en un mínimo en el centroide y se harán mayores a medida que nos alejemos del centroide.

Aunque esto complica nuestro análisis, lo bueno es que el cambio en el momento de inercia es predecible. Siempre será como mínimo cuando tomemos el momento de inercia sobre el centroide, o un eje que atraviesa el centroide. Este mínimo, al que llamaremos\(I_C\), es el valor que buscaremos en nuestra tabla de momentos de inercia. A partir de este valor mínimo, o no ajustado, podemos encontrar el valor del momento de inercia sobre cualquier punto\(I_P\) agregando un factor de ajuste igual al área por distancia al cuadrado para los momentos de inercia de área, o masa por distancia al cuadrado para momentos de inercia de masa.

\[ I_{xxP} = I_{xxC} + A * r^2 \]

\[ I_{xxP} = I_{xxC} + m * r^2 \]

Este proceso de ajuste con las ecuaciones anteriores es el teorema del eje paralelo. Los términos área o masa simplemente representan el área o masa de la parte que estás mirando, mientras que la distancia (\(r\)) representa la distancia que estamos moviendo el eje sobre el cual estamos tomando el momento de inercia. Esta puede ser una distancia vertical, una distancia horizontal o una diagonal dependiendo del eje sobre el que se tome el momento de inercia.

Un rectángulo tiene un sistema de coordenadas XY centrado en su centroide, con el origen de este sistema etiquetado C. Otro sistema de coordenadas XY, con la misma orientación y el origen etiquetado P, se ubica a cierta distancia por debajo del rectángulo con el eje y alineado verticalmente con el lado izquierdo del rectángulo. r_x representa la distancia vertical entre los ejes x del sistema de coordenadas C y el sistema de coordenadas P. r_y representa la distancia horizontal entre los ejes y del sistema de coordenadas C y el sistema de coordenadas P. El eje z no se muestra pero se puede suponer que apunta directamente fuera de la pantalla desde sus respectivos orígenes; r_z representa la distancia diagonal entre los puntos C y P, o la distancia entre los ejes z de estos sistemas de coordenadas. — Figura\(\PageIndex{2}\): La distancia (\(r\)) en el Teorema del Eje Paralelo representa la distancia que estamos moviendo el eje sobre el que estamos tomando el momento de inercia.

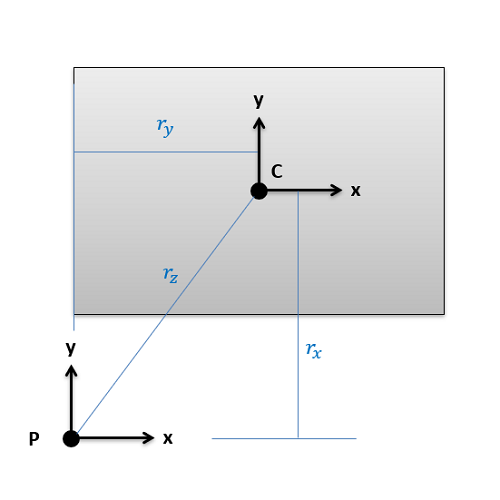
Digamos que estamos tratando de encontrar los momentos de inercia del rectángulo arriba sobre punto\(P\). Comenzaríamos por mirar hacia arriba\(I_{xx}\),\(I_{yy}\), y\(J_{zz}\) sobre el centroide del rectángulo (\(C\)) en el momento de la tabla de inercia. Entonces agregaríamos un término área-tiempos-distancia-cuadrado a cada uno para encontrar los momentos ajustados de inercia sobre\(P\). La distancia por la que estamos moviendo el\(x\) eje\(I_{xx}\) es la distancia vertical\(r_x\), la distancia por la que estamos moviendo el\(y\) eje\(I_{yy}\) es la distancia horizontal\(r_y\), y la distancia que moveríamos el\(z\) eje -eje (que está apuntando fuera de la página) para\(J_{zz}\) es la distancia diagonal\(r_z\).

Los ajustes de centro de masa siguen una lógica similar, usando masa tiempos distancia al cuadrado, donde la distancia representa hasta qué punto se está moviendo el eje de rotación en el espacio tridimensional.

Uso del método de piezas compuestas para encontrar el momento de inercia

Para encontrar el momento de inercia de un cuerpo usando el método de piezas compuestas, debe comenzar dividiendo su área o volumen hacia abajo en formas simples. Asegúrese de que cada forma individual esté disponible en el momento de la mesa de inercia, y puede tratar agujeros o recortes como área negativa o masa.

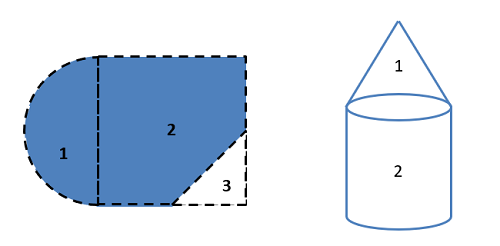
Una forma bidimensional se divide en tres partes componentes: 1 - un semicírculo con el borde recto hacia la derecha; 2 - un cuadrado adyacente al borde recto del semicírculo; 3 - un recorte triangular que elimina la esquina inferior derecha del cuadrado. Una forma tridimensional se divide en dos partes componentes: 1 - un cilindro vertical; 2 - un cono cuya base es la parte superior del cilindro. — Figura\(\PageIndex{3}\): Comience por desglosar su área o volumen en partes simples, y numerar esas partes. Los agujeros o recortes contarán como áreas o masas negativas.

A continuación vas a crear una tabla para hacer un seguimiento de los valores. Dedica una fila a cada parte que hayas numerado anteriormente, e incluye una fila final de “total” que se utilizará para algunos valores. La mayor parte del trabajo del método de piezas compuestas es llenar en esta tabla. Las columnas variarán ligeramente con lo que buscas, pero generalmente necesitarás lo siguiente.

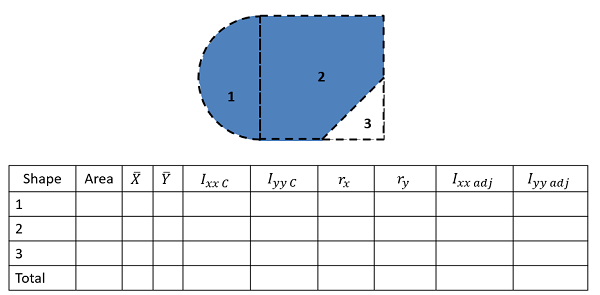
Aquí se repite la forma bidimensional de la Figura 3 anterior, compuesta por tres formas simples de componentes. Una tabla debajo de la forma muestra el área de cada pieza componente, las coordenadas x e y del centroide y los momentos de inercia sobre los ejes x e y si se consideran aisladamente, la distancia de ajuste r para los ejes x e y del centroide de la pieza a los ejes de la forma general, y los momentos ajustados de la pieza sobre los ejes x e y en relación con la forma compuesta. Una fila adicional contiene los valores totales de toda la forma para cada una de estas cantidades. — Figura\(\PageIndex{4}\): La mayor parte del trabajo en el método de piezas compuestas girará en torno al llenado de una mesa como esta. Esta tabla contiene las filas y columnas necesarias para encontrar los momentos de inercia del área rectangular (\(I_{xx}\)y\(I_{yy}\)) para este cuerpo compuesto.

El área o masa para cada pieza (área para momentos de inercia de área o masa para momentos de inercia de masa). Recuerde que los recortes deben ser listados como áreas o masas negativas.
Las ubicaciones del centroide o centro de masa (\(x\)\(y\)y posiblemente\(z\) las coordenadas). La mayor parte del tiempo, estaremos encontrando el momento de inercia sobre el centroide de la forma compuesta, y si eso no se le da explícitamente a usted, necesitará encontrarlo antes de ir más allá. Para más detalles sobre esto, consulte la página Centroides y Centros de Masa vía Método de Partes Compuestas.
El momento de inercia valora alrededor del centroide de cada forma. Para encontrar estos valores conectarás números para altura, radio, masa, etc. en fórmulas en la tabla de momento de inercia. Sin embargo, no uses estas fórmulas ciegamente, ya que es posible que necesites rotar mentalmente el cuerpo, y así cambiar las ecuaciones, si la orientación de la forma en la tabla no coincide con la orientación de la forma en tu diagrama.
Las distancias de ajuste (\(r\)) para cada forma. Para este valor querrás determinar qué tan lejos se mueve el\(x\) -eje,\(y\) -eje o\(z\) -eje para ir desde el centroide de la pieza hasta el centroide general o punto sobre el que estás tomando el momento de inercia. Para calcular estos valores, generalmente encontrará las distancias horizontales, verticales o diagonales entre los centroides de pieza y los centroides generales que haya enumerado anteriormente en la tabla. Consulte la sección del teorema del eje paralelo de esta página anterior para más detalles.
Por último, tendrás una columna de los momentos ajustados de inercia. Tome el momento original de inercia sobre el centroide, luego simplemente agregue su término de tiempos de área o\(r^2\) término de tiempo\(r^2\) de masa para este valor ajustado.

El momento general de inercia de tu cuerpo compuesto es simplemente la suma de todos los momentos ajustados de inercia para las piezas, que será la suma de los valores en la última columna (o columnas, si estás encontrando los momentos de inercia alrededor de más de un eje).

Video\(\PageIndex{1}\): Videoconferencia que cubre esta sección, impartida por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/zulGTSWF6xs.

Ejemplo\(\PageIndex{1}\)

Utilice el teorema del eje paralelo para encontrar el momento de inercia de masa de esta esbelta varilla con masa\(m\) y longitud\(L\) alrededor del\(z\) eje -en su punto final.

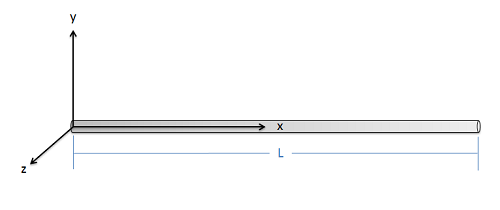
Un sistema de coordenadas cartesianas tridimensional, con el eje z apuntando fuera de la pantalla y el eje x acostado horizontalmente en el plano de la pantalla. Una varilla esbelta de longitud L se encuentra a lo largo del eje x positivo con su punto final izquierdo en el origen. — Figura\(\PageIndex{5}\): diagrama de problemas para Ejemplo\(\PageIndex{1}\). Una varilla se encuentra a lo largo del\(x\) eje positivo de un sistema de coordenadas cartesianas, con su punto final izquierdo localizado en el origen.

Solución:: Video\(\PageIndex{2}\): Solución trabajada a problema de ejemplo\(\PageIndex{1}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/4oN0kgDO3Yw.

Ejemplo\(\PageIndex{2}\)

Una viga se realiza conectando dos vigas de 2" x 4" en un patrón en T con la sección transversal como se muestra a continuación. Determinar la ubicación del centroide de esta sección transversal combinada y luego encontrar el momento de inercia del área rectangular alrededor del\(x\) eje -a través del punto centroide.

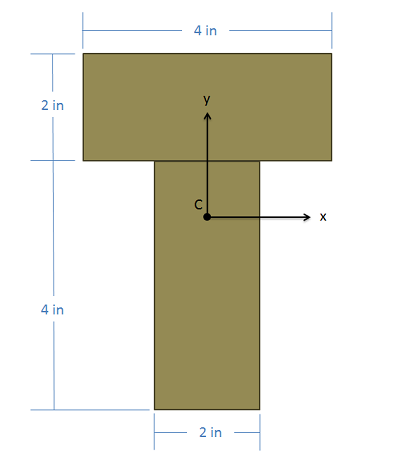
Una viga en forma de T se realiza conectando una viga vertical de 2 por 4 pulgadas al centro del borde inferior de una viga horizontal de 2 por 4 pulgadas. — Figura\(\PageIndex{6}\): diagrama de problemas para Ejemplo\(\PageIndex{2}\). El borde superior de una viga vertical de 2" x 4" está centrado y conectado al borde inferior de una viga horizontal de 2" x 4", creando un ensamblaje en forma de T.

Solución:: Video\(\PageIndex{3}\): Solución trabajada a problema de ejemplo\(\PageIndex{2}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/lgXlp2lRaiA.

Ejemplo\(\PageIndex{3}\)

Una mancuerna consta de dos esferas de diámetro 0.2 metros, cada una con una masa de 40 kg, unidas a los extremos de una varilla esbelta de 0.6 metros de largo de masa 20 kg. Determinar el momento de inercia de masa de la mancuerna alrededor del\(y\) eje -que se muestra en el diagrama.

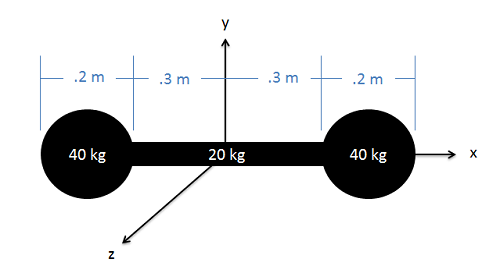
Un plano de coordenadas cartesianas tridimensional, con el eje z apuntando fuera de la página, el eje x acostado horizontalmente en el plano de la pantalla y el eje y acostado verticalmente en el plano de la pantalla. Una mancuerna consiste en una varilla delgada de 0.6 metros de largo que se extiende a lo largo del eje x, con su punto medio en el origen, con una esfera de 0.2 metros de diámetro unida a cada punto final de la varilla. Todo el conjunto es de 1 metro de largo. — Figura\(\PageIndex{7}\): diagrama de problemas para Ejemplo\(\PageIndex{3}\). Una mancuerna consiste en una varilla esbelta con una esfera unida a cada extremo que se extiende a lo largo del\(x\) eje -de un sistema de coordenadas cartesianas, con su punto medio en el origen.

Solución:: Video\(\PageIndex{4}\): Solución trabajada a problema de ejemplo\(\PageIndex{3}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/ufewJ7CmvIs.