2.1: Interpolación de Funciones Univariadas

El objetivo de la interpolación es aproximar el comportamiento de una función subyacente verdadera utilizando valores de función en un número limitado de puntos. La interpolación sirve a dos propósitos importantes y distintos a lo largo de este libro. En primer lugar, se trata de una herramienta matemática que facilita el desarrollo y análisis de técnicas numéricas para, por ejemplo, integrar funciones y resolver ecuaciones diferenciales. En segundo lugar, la interpolación se puede utilizar para estimar o inferir el comportamiento de la función en función de los valores de función registrados como una tabla, por ejemplo recopilados en un experimento (es decir, búsqueda de tablas).

Definamos el problema de interpolación para una función univariada, es decir, una función de una sola variable. Discretizamos el dominio\(\left[x_{1}, x_{N}\right]\) en segmentos\(N-1\) no superpuestos\(\left\{S_{1}, \ldots, S_{N-1}\right\}\), utilizando\(N\) puntos\(\left\{x_{1}, \ldots, x_{N}\right\}\), como se muestra en la Figura 2.1. Cada segmento se define por\[S_{i}=\left[x_{i}, x_{i+1}\right], \quad i=1, \ldots, N-1,\] y denotamos la longitud del segmento por\(h\), es decir,\[h \equiv x_{i+1}-x_{i} .\] Por simplicidad, asumimos que\(h\) es constante en todo el dominio. La discretización es un concepto que se utiliza a lo largo del análisis numérico para aproximar un sistema continuo (problema infinito-dimensional) como un sistema discreto (problema finito-dimensional) para que la solución pueda estimarse usando una computadora. Para la interpolación, la discretización se caracteriza por el tamaño del segmento\(h\); más pequeño\(h\) es generalmente más preciso pero más costoso.

Supongamos que, en el segmento\(S_{i}\), se nos dan puntos\(M\) de interpolación\[\bar{x}^{m}, \quad m=1, \ldots, M\]

Figura 2.1: Discretización de un dominio 1-D en\(N-1\) segmentos.

a) discretización

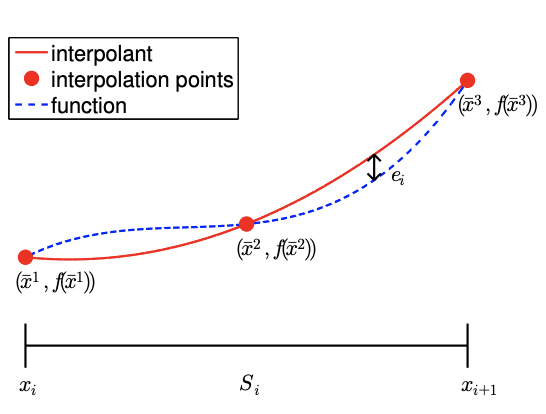
b) interpolación local

Figura 2.2: Ejemplo de un dominio 1-D discretizado en cuatro segmentos, un segmento local con puntos de evaluación de\(M=3\) función (es decir, puntos de interpolación) y puntos de evaluación de función global (izquierda). Construcción de un interpolante en un segmento (derecha).

y los valores de función asociados\[f\left(\bar{x}^{m}\right), \quad m=1, \ldots, M\] Deseamos aproximar\(f(x)\) para cualquier dado\(x\) en\(S_{i}\). Específicamente, deseamos construir un interpolante Si eso se aproxima\(f\) en el sentido que\[(\mathcal{I} f)(x) \approx f(x), \quad \forall x \in S_{i},\] y satisface\[(\mathcal{I} f)\left(\bar{x}^{m}\right)=f\left(\bar{x}^{m}\right), \quad m=1, \ldots, M .\] Tenga en cuenta que, por definición, el interpolante coincide con el valor de la función en los puntos de interpolación,\(\left\{\bar{x}^{m}\right\}\).

La relación entre la discretización, un segmento local y los puntos de interpolación se ilustra en la Figura 2.2 (a). El dominio\(\left[x_{1}, x_{5}\right]\) se discretiza en cuatro segmentos, delineados por los puntos\(x_{i}, i=1, \ldots, 5\). Por ejemplo, el segmento\(S_{2}\) está definido por\(x_{2}\) y\(x_{3}\) y tiene una longitud característica\(h=x_{3}-x_{2}\). La Figura\(2.2\) (b) ilustra la construcción de un interpolante en el segmento\(S_{2}\) usando puntos de\(M=3\) interpolación. Tenga en cuenta que solo usamos el conocimiento de la función evaluada en los puntos de interpolación para construir el interpolante. En general, los puntos que delimitan los segmentos,\(x_{i}\), no necesitan ser puntos de evaluación de funciones\(\tilde{x}_{i}\), como veremos en breve.

También podemos utilizar la técnica de interpolación en el contexto de la búsqueda de tablas, donde una tabla consiste en valores de función evaluados en un conjunto de puntos, es decir,\(\left(\tilde{x}_{i}, f\left(\tilde{x}_{i}\right)\right)\). Dado un punto de interés\(x\), primero encontramos el segmento en el que reside el punto, identificándonos\(S_{i}=\left[x_{i}, x_{i+1}\right]\) con\(x_{i} \leq x \leq x_{i+1}\). Luego, identificamos en el segmento\(S_{i}\) los pares de evaluación\(\left(\tilde{x}_{j}, f\left(\tilde{x}_{j}\right)\right), j=\ldots, \Rightarrow\left(\bar{x}^{m}, f\left(\bar{x}^{m}\right)\right)\),\(m=1, \ldots, M\). Finalmente, calculamos el interpolante en\(x\) para obtener una aproximación a\(f(x)\),\((\mathcal{I} f)(x)\).

(Tenga en cuenta que, si bien usamos segmentos fijos y no superpuestos para construir nuestro interpolante en este capítulo, podemos ser más flexibles en la elección de segmentos en general. Por ejemplo, para estimar el valor de una función en algún momento\(x\), podemos elegir un conjunto de puntos de\(M\) datos en la vecindad de\(x\). Usando los\(M\) puntos, construimos un interpolante local como en la Figura 2.2 (b) e inferimos\(f(x)\) evaluando el interpolante en\(x\). Obsérvese que el interpolante local construido de esta manera define implícitamente un segmento local. El segmento se “desliza” con el objetivo\(x\), es decir, se elige adaptativamente. En el capítulo actual sobre interpolación y en Capítulo\(\underline{7}\) sobre integración, enfatizaremos la perspectiva de segmento fijo; sin embargo, al discutir la diferenciación en Capítulo\(\underline{3}\), adoptaremos la perspectiva de segmento deslizante.)

Para evaluar la calidad del interpolante, definimos su error como la diferencia máxima entre la función verdadera y el interpolante en el segmento, es decir,\[e_{i} \equiv \max _{x \in S_{i}}|f(x)-(\mathcal{I} f)(x)| .\] Debido a que la construcción de un interpolante en un segmento dado es independiente de la de otro segmento\(^{1}\), podemos analizar el error de interpolación local un segmento a la vez. La localidad de construcción de interpolación y error simplifica enormemente el análisis de errores. Además, definimos el error máximo de interpolación,\(e_{\max }\), como el error máximo sobre todo el dominio, que es equivalente al mayor de los errores de segmento, es decir\[e_{\max } \equiv \max _{i=1, \ldots, N-1} e_{i}\] El error de interpolación es una medida que utilizamos para evaluar la calidad de diferentes esquemas de interpolación. Específicamente, para cada esquema de interpolación, vinculamos el error en términos de la función\(f\) y el parámetro de discretización\(h\) para entender cómo cambia el error a medida que se refina la discretización.

Consideremos un ejemplo de interpolante.

Ejemplo 2.1.1 constante por tramos, punto final izquierdo

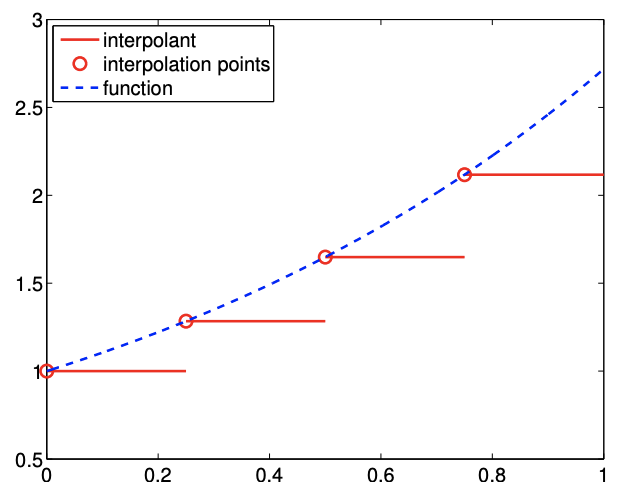
El primer ejemplo que consideramos utiliza un polinomio constante por partes para aproximar la función\(f\). Debido a que un polinomio constante es parametrizado por un solo valor, este esquema requiere un punto de interpolación por intervalo, es decir\(M=1\). En cada segmento\(S_{i}=\left[x_{i}, x_{i+1}\right]\), elegimos el punto final izquierdo como nuestro punto de interpolación, es decir,\[\bar{x}^{1}=x_{i}\] Como se muestra en la Figura\(2.3\), también podemos asociar fácilmente los puntos de segmentación,\(x_{i}\), con los puntos de evaluación de la función global,\(\tilde{x}_{i}\), i.e. \[\tilde{x}_{i}=x_{i}, \quad i=1, \ldots, N-1\]Extendiendo el valor de punto final izquierdo al resto del segmento, obtenemos el interpolante de la forma\[(\mathcal{I} f)(x)=f\left(\bar{x}^{1}\right)=f\left(\tilde{x}_{i}\right)=f\left(x_{i}\right), \quad \forall x \in S_{i}\] Figura 2.4 (a) muestra el esquema de interpolación aplicado a\(f(x)=\exp (x)\) over\([0,1]\) con\(N=\) 5. Porque\(f^{\prime}>0\) en cada intervalo, el interpolante\(\mathcal{I} f\) siempre subestima el valor de\(f\). Por el contrario, si\(f^{\prime}<0\) sobre un intervalo, el interpolante sobreestima los valores de\(f\) en el intervalo. El interpolante es exacto a lo largo del intervalo si\(f\) es constante.

Si\(f^{\prime}\) existe, el error en el interpolante está limitado por\[e_{i} \leq h \cdot \max _{x \in S_{i}}\left|f^{\prime}(x)\right|\]\({ }^{1}\) para los interpolantes considerados en este capítulo

Figura 2.3: La relación entre la discretización, un segmento local y los puntos de evaluación de funciones para un interpolante de punto final izquierdo y constante por partes.

(a) interpolante

(b) error

Figura 2.4: Interpolante de punto final izquierdo, constante por tramos.

Dado que\(e_{i}=\mathcal{O}(h)\) y las escalas de error como la primera potencia de\(h\), se dice que el esquema es preciso de primer orden. El comportamiento de convergencia del interpolante aplicado a la función exponencial se muestra en la Figura 2.4 (b), donde el valor máximo del error de interpolación\(e_{\max }=\max _{i} e_{i}\),, se traza en función del número de intervalos,\(1 / h\).

Hacemos una pausa para revisar dos conceptos relacionados que caracterizan el comportamiento asintótico de una secuencia: la\(\mathcal{O}\) notación grande\((\mathcal{O}(\cdot))\) y la notación asintótica\((\sim)\). Decir eso\(Q\) y\(z\) son cantidades escalares (números reales) y\(q\) es una función de\(z\). Usando la\(\mathcal{O}\) notación grande, cuando decimos que\(Q\) es\(\mathcal{O}(q(z)\)) como\(z\) tiende a, digamos, cero (o infinito), queremos decir que existen constantes\(C_{1}\) y\(z^{*}\) tal que \(|Q|<C_{1}|q(z)|, \forall z<z^{*}\)(o\(\forall z>z^{*}\)). Por otro lado, utilizando la notación asintótica, cuando decimos que\(Q \sim C_{2} q(z)\) como\(z\) tiende a algún límite, queremos decir que existe una constante\(C_{2}\) (no necesaria igual a\(\left.C_{1}\right)\) tal que\(Q /\left(C_{2} q(z)\right)\) tiende a la unidad como \(z\)tiende hasta el límite. Utilizaremos estas notaciones en dos casos en particular: (i) cuando\(z\) es\(\delta\), un parámetro de discretización (\(h\)en nuestro ejemplo anterior) - que tiende a cero; (ii) cuando\(z\) es\(K\), un entero relacionado con el número de grados de libertad que definen un problema (\(N\)en nuestro ejemplo anterior) - que tiende al infinito. Tenga en cuenta que no necesitamos preocuparnos por pequeños efectos con la notación\(\mathcal{O}\) (o la asintótica): porque\(K\) tiende al infinito, por ejemplo,\(\mathcal{O}(K)=\mathcal{O}(K-1)=\mathcal{O}(K+\sqrt{K})\). Por último, observamos que la expresión\(Q=\mathcal{O}(1)\) significa que\(Q\) efectivamente no depende de algún parámetro (implícito, o “entendido”),\(z .^{2}\)

Si\(f(x)\) es lineal, entonces el límite de error se puede mostrar usando un argumento directo. Vamos\(f(x)=\overline{m x}+b\). La diferencia entre la función y el interpolante sobre\(S_{i}\) es\[f(x)-(\mathcal{I} f)(x)=[m x-b]-\left[m \bar{x}^{1}-b\right]=m \cdot\left(x-\bar{x}^{1}\right) .\] Recordando el error local es la diferencia máxima en la función y el interpolante y señalando que\(S_{i}=\left[x_{i}, x_{i+1}\right]=\left[\bar{x}^{1}, \bar{x}^{1}+h\right]\), obtenemos\[e_{i}=\max _{x \in S_{i}}|f(x)-(\mathcal{I} f)(x)|=\max _{x \in S_{i}}\left|m \cdot\left(x-\bar{x}^{1}\right)\right|=|m| \cdot \max _{x \in\left[\bar{x}^{1}, \bar{x}^{1}+h\right]}\left|x-\bar{x}^{1}\right|=|m| \cdot h .\] Finalmente, recordando que\(m=f^{\prime}(x)\) para el lineal función, tenemos\(e_{i}=\left|f^{\prime}(x)\right| \cdot h\). Ahora bien, probemos el error encuadernado para un general\(f\).

Prueba

La prueba se desprende de la definición del interpolante y del teorema fundamental del cálculo, es decir,\[f(x)-(\mathcal{I} f)(x)=f(x)-f\left(\bar{x}^{1}\right) \quad \text { (by definition of }(\mathcal{I} f) \text { ) }\]\[\begin{aligned} & =\int_{\bar{z} 1}^{x} f^{\prime}(\xi) d \xi \quad \text { (fundamental theorem of calculus) } \\ & \leq \int_{\bar{x}^{1}}^{x}\left|f^{\prime}(\xi)\right| d \xi \\ & \leq \max _{x \in\left[\bar{x}^{1}, x\right]}\left|f^{\prime}(x)\right|\left|\int_{\bar{x}^{1}}^{x} d \xi\right| \end{aligned}\] (desigualdad de Hölder)\[\begin{aligned} & \leq \max _{x \in S_{i}}\left|f^{\prime}(x)\right| \cdot h, \quad \forall x \in S_{i}=\left[\bar{x}^{1}, \bar{x}^{1}+h\right] . \end{aligned}\] Sustitución de la expresión en la definición de los rendimientos\[e_{i} \equiv \max _{x \in S_{i}}|f(x)-(\mathcal{I} f)(x)| \leq \max _{x \in S_{i}}\left|f^{\prime}(x)\right| \cdot h .\]\({ }^{2}\) de error La notación de ingeniería \(Q=\mathcal{O}\left(10^{3}\right)\)es algo diferente y realmente solo significa que el número es aproximadamente\(10^{3} .\)

\({ }^{2}\)La notación de ingeniería\(Q=\mathcal{O}\left(10^{3}\right)\) es algo diferente y realmente solo significa que el número es aproximadamente\(10^{3} .\)

(a) interpolante

(b) error

Figura 2.5: Interpolante de punto final izquierdo, constante por tramos para una función no suave.

Es importante señalar que la prueba se basa en la suavidad de\(f\). De hecho, si\(f\) es discontinuo y\(f^{\prime}\) no existe, entonces\(e_{i}\) puede serlo\(\mathcal{O}(1)\). En otras palabras, el interpolante no converge a la función (en el sentido de error máximo), aunque el\(h\) sea refinado. Para demostrarlo, consideremos una función\[f(x)=\left\{\begin{array}{ll} \sin (\pi x), & x \leq \frac{1}{3} \\ \frac{1}{2} \sin (\pi x), & x>\frac{1}{3} \end{array},\right.\] que es discontinua en\(x=1 / 3\). El resultado de aplicar la constante por tramos, regla de punto final izquierdo a la función se muestra en la Figura 2.5 (a). Observamos que la solución en el tercer segmento no se aproxima bien debido a la presencia de la discontinuidad. Más importante aún, la gráfica de convergencia, Figura 2.5 (b), confirma que el error máximo de interpolación no converge aunque\(h\) sea refinado. Esta reducción en la tasa de convergencia para funciones no suaves no es exclusiva de esta regla de interpolación en particular; todas las reglas de interpolación sufren de este problema. Por lo tanto, debemos tener cuidado cuando interpolamos una función no suave.

Finalmente, comentamos la distinción entre el “mejor ajuste” (en alguna norma, o métrica) y el interpolante. El mejor ajuste en la norma “max” o “sup” de una función constante\(c_{i}\) a\(f(x)\) sobre\(S_{i}\) minimiza\(\left|c_{i}-f(x)\right|\) sobre\(S_{i}\) y normalmente será diferente y por fuerza mejor (en la norma elegida) que el interpolante. Sin embargo, la determinación de\(c_{i}\) en principio requiere el conocimiento de\(f(x)\) en (casi) todos los puntos en\(S_{i}\) mientras que el interpolante solo requiere conocimiento de\(f(x)\) en un punto - de ahí mucho más útil. Esto se discute más a fondo en la Sección 2.1.1.

Definamos de manera más formal algunos de los conceptos clave visitados en el primer ejemplo. Si bien introducimos los siguientes conceptos en el contexto del análisis de los esquemas de interpolación, los conceptos se aplican de manera más general al análisis de diversos esquemas numéricos.

• La precisión relaciona qué tan bien el esquema numérico (finito-dimensional) se aproxima al sistema continuo (infinito-dimensional). En el contexto de la interpolación, la precisión indica qué tan bien se\(\mathcal{I} f\) aproxima el interpolante\(f\) y se mide por el error de interpolación,\(e_{\max }\). - Convergencia es la propiedad de que el error desaparece a medida que se refina la discretización, i.e.

\[e_{\max } \rightarrow 0 \quad \text { as } \quad h \rightarrow 0 .\]Un esquema convergente puede lograr cualquier precisión (error) deseada en la aritmética de predicción infinita eligiendo\(h\) suficientemente pequeña. El interpolante de punto final izquierdo, constante a trozos, es un esquema convergente, porque\(e_{\max }=\mathcal{O}(h)\), y\(e_{\max } \rightarrow 0\) como\(h \rightarrow 0\).

• La tasa de convergencia es la potencia\(p\) tal que

\[e_{\max } \leq C h^{p} \quad \text { as } \quad h \rightarrow 0,\]donde\(C\) es una constante independiente de\(h\). El esquema es de primer orden exacto para\(p=1\), segundo orden exacto para\(p=2\), y así sucesivamente. El interpolante de punto final izquierdo constante a trozos es preciso de primer orden porque\(e_{\max }=C h^{1}\). Tenga en cuenta\(p\) que aquí es fija y la convergencia (con número de intervalos) es así algebraica.

Obsérvese que normalmente como\(h \rightarrow 0\) obtenemos no un comportamiento atado sino de hecho asintótico:\(e_{\max } \sim\)\(C h^{p}\) o equivalentemente,\(e_{\max } /\left(C h^{p}\right) \rightarrow 1\), as\(h \rightarrow 0\). Tomando el logaritmo de\(e_{\max } \sim C h^{p}\), obtenemos\(\ln \left(e_{\max }\right) \sim \ln C+p \ln h\). Así, una\(\log -\log\) parcela es un medio conveniente de encontrar\(p\) empíricamente.

• La resolución es la longitud característica\(h_{\text {crit }}\) para cualquier problema en particular (descrito por\(f\)) para el cual vemos la tasa de convergencia asintótica para\(h \leq h_{\text {crit. }}\). La gráfica de convergencia en la Figura\(2.4\) (b) muestra que el interpolante de punto final izquierdo, constante por tramos, logra la tasa de convergencia asintótica de 1 con respecto a\(h\) for\(h \leq 1 / 2\); tenga en cuenta que la pendiente de\(h=1\) a\(h=1 / 2\) es menor que la unidad. Así,\(h_{\text {crit }}\) para el esquema de interpolación aplicado a\(f(x)=\exp (x)\) es aproximadamente\(1 / 2\).
• Costo computacional o conteo de operaciones es el número de operaciones de punto flotante (\({ }^{3}\)FLOP) a calcular\(I_{h}\). Como\(h \rightarrow 0\), se acerca el número de FLOP\(\infty\). El escalado del costo de cálculo con el tamaño del problema se conoce como complejidad computacional. El tiempo de ejecución real del cálculo es una función del costo computacional y del hardware. El costo de construir el interpolante de punto final izquierdo constante por tramos es proporcional al número de segmentos. Así, el costo escala linealmente con\(N\), y se dice que el esquema tiene complejidad lineal.
• La memoria o almacenamiento es el número de números de punto flotante que se deben almacenar en cualquier momento durante la ejecución.

Observamos que las propiedades anteriores caracterizan un esquema en representación de precisión infinita y aritmética. La precisión está relacionada con la precisión de la máquina, truncamiento de números de punto flotante, redondeo y errores aritméticos, etc., todos los cuales están ausentes en la aritmética de precisión infinita.

También observamos que hay dos demandas conflictivas; la precisión del esquema aumenta con la disminución\(h\) (asumiendo que el esquema es convergente), pero el costo computacional aumenta con la disminución\(h\). Intuitivamente, esto siempre sucede porque la dimensión de la aproximación discreta debe aumentarse para aproximarse mejor al sistema continuo. Sin embargo, algunos esquemas producen un error menor para el mismo costo computacional que otros esquemas. El desempeño de un esquema numérico se evalúa en términos de la precisión que entrega para un costo computacional dado.

Ahora visitaremos varios otros esquemas de interpolación y caracterizaremos los esquemas usando las propiedades anteriores.

\({ }^{3}\)No debe confundirse con los FLOPS (operaciones de punto flotante por segundo), que a menudo se utiliza para medir el rendimiento de un hardware computacional.

Figura 2.6: Interpolante de punto final derecho, constante por tramos.

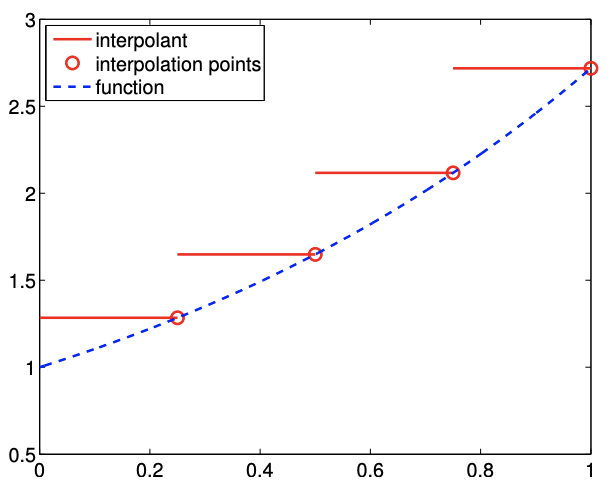
Ejemplo 2.1.2 constante por pieza, punto final derecho

Este interpolante también utiliza un polinomio constante por partes para aproximar la función\(f\), y por lo tanto requiere un punto de interpolación por intervalo, es decir,\(M=1\). Esta vez, el punto de interpolación está en el punto final derecho, en lugar del extremo izquierdo, dando como resultado Los puntos de evaluación de\[\bar{x}^{1}=x_{i+1}, \quad(\mathcal{I} f)(x)=f\left(\bar{x}^{1}\right)=f\left(x_{i+1}\right), \quad \forall x \in S_{i}=\left[x_{i}, x_{i+1}\right] .\] la función global\(\tilde{x}_{i}\),, están relacionados con los puntos de segmentación\(x_{i}\),, por\[\tilde{x}_{i}=x_{i+1}, \quad i=1, \ldots, N-1 .\] Figura\(2.6\) muestra la interpolación aplicado a la función exponencial.

Si\(f^{\prime}\) existe, el error en el interpolante está limitado por\[e_{i} \leq h \cdot \max _{x \in S_{i}}\left|f^{\prime}(x)\right|,\] y por lo tanto el esquema es preciso de primer orden. La prueba es similar a la del interpolante de punto final derecho, constante por partes.

Ejemplo 2.1.3 constante por pieza, punto medio

Este interpolante utiliza un polinomio constante por partes para aproximar la función\(f\), pero usa el punto medio del segmento, como punto de interpolación\(S_{i}=\left[x_{i}, x_{i+1}\right]\), es decir,\[\bar{x}^{1}=\frac{1}{2}\left(x_{i}+x_{i+1}\right) .\] Denotando el punto de evaluación de la función (global) asociado con el segmento\(S_{i}\) como \(\tilde{x}_{i}\), tenemos\[\tilde{x}_{i}=\frac{1}{2}\left(x_{i}+x_{i+1}\right), \quad i=1, \ldots, N-1,\] como se ilustra en la Figura 2.7. Tenga en cuenta que los puntos de segmentación\(x_{i}\) no corresponden a los puntos de evaluación de la función\(\tilde{x}_{i}\) a diferencia de los dos interpolantes anteriores. Esta elección del punto de interpolación da como resultado el interpolante\[(\mathcal{I} f)(x)=f\left(\bar{x}^{1}\right)=f\left(\tilde{x}_{i}\right)=f\left(\frac{1}{2}\left(x_{i}+x_{i+1}\right)\right), \quad x \in S_{i} .\]

Figura 2.7: La relación entre la discretización, un segmento local y los puntos de evaluación de funciones para un interpolante de punto medio, constante por partes.

La Figura 2.8 (a) muestra el interpolante para la función exponencial. En el contexto de la búsqueda de tablas, este interpolante surge naturalmente si un valor se aproxima a partir de una tabla de datos eligiendo el punto de datos más cercano.

El error del interpolante está limitado por\[e_{i} \leq \frac{h}{2} \cdot \max _{x \in S_{i}}\left|f^{\prime}(x)\right|,\] donde el factor de la mitad proviene del hecho de que cualquier punto de evaluación de función está a menos de\(h / 2\) distancia de uno de los puntos de interpolación. La figura\(2.8(\mathrm{a})\) muestra que el interpolante de punto medio logra un error menor que el interpolante de punto final izquierdo o derecho. Sin embargo, el error sigue escalando linealmente con\(h\), y así el interpolante de punto medio es preciso de primer orden.

Para una función lineal\(f(x)=m x+b\), el límite de error agudo se puede obtener a partir de un argumento directo. La diferencia entre la función y su interpolante de punto medio es\[f(x)-(\mathcal{I} f)(x)=[m x+b]-\left[m \bar{x}^{1}+b\right]=m \cdot\left(x-\bar{x}^{1}\right) .\] La diferencia desaparece en el punto medio, y aumenta linealmente con la distancia desde el punto medio. Así, la diferencia se maximiza en cualquiera de los puntos finales. Al señalar que el segmento se puede expresar como\(S_{i}=\left[x_{i}, x_{i+1}\right]=\left[\bar{x}^{1}-\frac{h}{2}, \bar{x}^{1}+\frac{h}{2}\right]\), el error máximo viene dado por\[\begin{aligned} e_{i} & \equiv \max _{x \in S_{i}}(f(x)-(\mathcal{I} f)(x))=\max _{x \in\left[\bar{x}^{1}-\frac{h}{2}, \bar{x}^{1}+\frac{h}{2}\right]}\left|m \cdot\left(x-\bar{x}^{1}\right)\right| \\ &=\left|m \cdot\left(x-\bar{x}^{1}\right)\right|_{x=\bar{x}^{1} \pm h / 2}=|m| \cdot \frac{h}{2} . \end{aligned}\] Recordando\(m=f^{\prime}(x)\) para la función lineal, tenemos\(e_{i}=\left|f^{\prime}(x)\right| h / 2\). Una prueba nítida para un general\(f\) sigue esencialmente la de la regla de punto final izquierdo constante por partes.

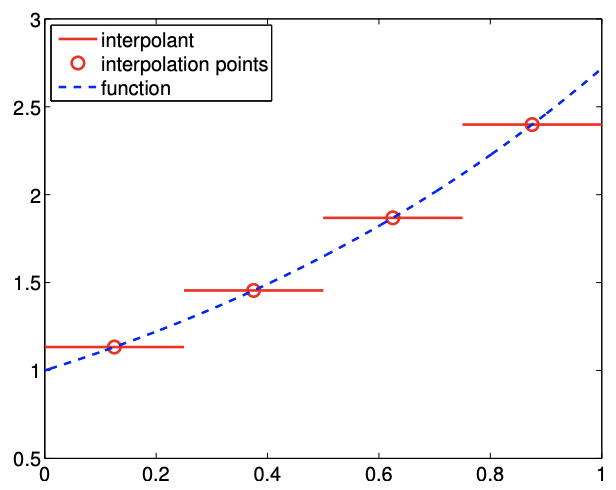
(a) interpolante

(b) error

Figura 2.8: Interpolante de punto medio, constante por tramos.

Prueba

La prueba se desprende del teorema fundamental del cálculo,\[\begin{aligned} f(x)-(\mathcal{I} f)(x) &=f(x)-f\left(\bar{x}^{1}\right)=\int_{\bar{x}^{1}}^{x} f^{\prime}(\xi) d \xi \leq \int_{\bar{x}^{1}}^{x}\left|f^{\prime}(\xi)\right| d \xi \leq \max _{x \in\left[\bar{x}^{1}, x\right]}\left|f^{\prime}(x)\right|\left|\int_{\bar{x}^{1}}^{x} d \xi\right| \\ & \leq \max _{x \in\left[\bar{x}^{1}-\frac{h}{2}, \bar{x}^{1}+\frac{h}{2}\right]}^{\left|f^{\prime}(x)\right| \cdot \frac{h}{2}, \quad \forall x \in S_{i}=\left[\bar{x}^{1}-\frac{h}{2}, \bar{x}^{1}+\frac{h}{2}\right]} \end{aligned}\] Así, tenemos\[e_{i}=\max _{x \in S_{i}}|f(x)-(\mathcal{I} f)(x)| \leq \max _{x \in S_{i}}\left|f^{\prime}(x)\right| \cdot \frac{h}{2}\]

Ejemplo 2.1.4 lineal en forma de pieza

Los tres ejemplos que hemos considerado hasta ahora utilizaron funciones constantes por partes para interpolar la función de interés, dando como resultado que los interpolantes sean precisos de primer orden. Para mejorar la calidad de la interpolación, consideramos un interpolante preciso de segundo orden en este ejemplo. Para lograr esto, elegimos una función lineal por partes (es decir, polinomios de primer grado) para aproximar el comportamiento de la función. Debido a que una función lineal tiene dos coeficientes, debemos elegir dos puntos de interpolación por segmento para definir de manera única el interpolante, es decir,\(M=2\). En particular, para el segmento\(S_{i}=\left[x_{i}, x_{i+1}\right]\), elegimos sus puntos finales,\(x_{i}\) y\(x_{i+1}\), como los puntos de interpolación, es decir,\[\bar{x}^{1}=x_{i} \quad \text { and } \quad \bar{x}^{2}=x_{i+1}\] Los puntos de evaluación de la función (global) y los puntos de segmentación están trivialmente relacionados por\[\tilde{x}_{i}=x_{i}, \quad i=1, \ldots, N,\]

Figura 2.9: Relación entre la discretización, un segmento local y los puntos de evaluación de funciones para un interpolante lineal.

como se ilustra en la Figura\(2.9\).

El interpolante resultante, definido usando la coordenada local, es de la forma\[(\mathcal{I} f)(x)=f\left(\bar{x}^{1}\right)+\left(\frac{f\left(\bar{x}^{2}\right)-f\left(\bar{x}^{1}\right)}{h}\right)\left(x-\bar{x}^{1}\right), \quad \forall x \in S_{i},\] o, en la coordenada global, se expresa como\[(\mathcal{I} f)(x)=f\left(x_{i}\right)+\left(\frac{f\left(x_{i+1}\right)-f\left(x_{i}\right)}{h_{i}}\right)\left(x-x_{i}\right), \quad \forall x \in S_{i} .\] La Figura\(2.10(\) a\()\) muestra el interpolante lineal aplicado a\(f(x)=\exp (x)\) over\([0,1]\) con \(N=5\). Tenga en cuenta que este interpolante es continuo a través de los puntos finales del segmento, porque cada función lineal por tramos coincide con los valores verdaderos de la función en sus puntos finales. Esto contrasta con los interpolantes parciales considerados en los tres ejemplos anteriores, los cuales fueron discontinuos a través de los puntos finales del segmento en general.

Si\(f^{\prime \prime}\) existe, el error del interpolante lineal está limitado por\[e_{i} \leq \frac{h^{2}}{8} \cdot \max _{x \in S_{i}}\left|f^{\prime \prime}(x)\right|\] El error del interpolante lineal converge cuadráticamente con la longitud del intervalo,\(h\). Debido a que el error escala con\(h^{2}\), se dice que el método es exacto de segundo orden. La Figura\(2.10\) (b) muestra que el interpolante lineal es significativamente más preciso que el interpolante lineal por tramos para la función exponencial. Esta tendencia es generalmente cierta para suficientes funciones suaves. Más importante aún, la convergencia de orden superior significa que el interpolante lineal se acerca a la función verdadera a una velocidad más rápida que el interpolante constante por tramos a medida que disminuye la longitud del segmento.

Demos un boceto de la prueba. Primero, al señalar que\(f(x)-(\mathcal{I} f)(x)\) desaparece en los puntos finales, expresamos nuestro error como\[f(x)-(\mathcal{I} f)(x)=\int_{\bar{x}^{1}}^{x}(f-\mathcal{I} f)^{\prime}(t) d t\] Siguiente, por el Teorema del Valor Medio (MVT), tenemos un punto\(x^{*} \in S_{i}=\left[\bar{x}^{1}, \bar{x}^{2}\right]\) tal que\(f^{\prime}\left(x^{*}\right)-\)\((\mathcal{I} f)^{\prime}\left(x^{*}\right)=0\). Tenga en cuenta el MVT - para una función continuamente diferenciable\(f\) existe un

(a) interpolante

(b) error

Figura 2.10: Interpolante lineal por tramos.

\(x^{*} \in\left[\bar{x}^{1}, \bar{x}^{2}\right]\)tal que se\(f^{\prime}\left(x^{*}\right)=\left(f\left(\bar{x}^{2}\right)-f\left(\bar{x}^{1}\right)\right) / h-\) desprende del Teorema de Rolle. El teorema de Rolle afirma que, para una función continuamente diferenciable\(g\) que se desvanece en\(\bar{x}^{1}\) y\(\bar{x}^{2}\), existe un punto\(x^{*}\) para el cual\(g^{\prime}\left(x^{*}\right)=0\). Para derivar el MVT tomamos\(g(x)=f(x)-\mathcal{I} f(x)\) para\(\mathcal{I} f\) dado por la Ec. (2.1). Aplicando nuevamente el teorema fundamental del cálculo, el error puede expresarse como\[\begin{aligned} f(x)-(\mathcal{I} f)(x) &=\int_{\bar{x}^{1}}^{x}(f-\mathcal{I} f)^{\prime}(t) d t=\int_{\bar{x}^{1}}^{x} \int_{x^{*}}^{t}(f-\mathcal{I} f)^{\prime \prime}(s) d s d t=\int_{\bar{x}^{1}}^{x} \int_{x^{*}}^{t} f^{\prime \prime}(s) d s d t \\ & \leq \max _{x \in S_{i}}\left|f^{\prime \prime}(x)\right| \int_{\bar{x}^{1}}^{x} \int_{x^{*}}^{t} d s d t \leq \frac{h^{2}}{2} \cdot \max _{x \in S_{i}}\left|f^{\prime \prime}(x)\right| \end{aligned}\] Este simple boceto muestra que el error de interpolación depende de la segunda derivada de\(f\) y varía cuadráticamente con la longitud del segmento\(h\); sin embargo, la constante no es agudo. A continuación se proporciona una prueba afilada.

Prueba

Nuestro objetivo es obtener un encuadernado\(|f(\hat{x})-\mathcal{I} f(\hat{x})|\) para un arbitrario\(\hat{x} \in S_{i}\). Si\(\hat{x}\) es el de los endpoints, el error de interpolación desaparece trivialmente; así, suponemos que no\(\hat{x}\) es uno de los endpoints. La prueba se desprende de una construcción de un interpolante cuadrático particular y de la aplicación del teorema de Rolle. Primero formemos el interpolante cuadrático,\(q(x)\), de la forma\[q(x) \equiv(\mathcal{I} f)(x)+\lambda w(x) \quad \text { with } \quad w(x)=\left(x-\bar{x}^{1}\right)\left(x-\bar{x}^{2}\right) .\] Dado que\((\mathcal{I} f)\) coincide\(f\) en\(\bar{x}^{1}\) y\(\bar{x}^{2}\) y\(q\left(\bar{x}^{1}\right)=q\left(\bar{x}^{2}\right)=0, q(x)\) coincide\(f\) en\(\bar{x}^{1}\) y\(\bar{x}^{2}\). Seleccionamos\(\lambda\) tal que\(q\) coincida\(f\) en\(\hat{x}\), es decir\[q(\hat{x})=(\mathcal{I} f)(\hat{x})+\lambda w(\hat{x})=f(\hat{x}) \Rightarrow \lambda=\frac{f(\hat{x})-(\mathcal{I} f)(\hat{x})}{w(\hat{x})}\] El error de interpolación del interpolante cuadrático viene dado por\[\phi(x)=f(x)-q(x)\] Porque\(q\) es el interpolante cuadrático de \(f\)definido por los puntos de interpolación\(\bar{x}^{1}, \bar{x}^{2}\), y\(\hat{x}, \phi\) tiene tres ceros en\(S_{i}\). Por el teorema de Rolle,\(\phi^{\prime}\) tiene dos ceros en\(S_{i}\). Nuevamente, por el teorema de Rolle,\(\phi^{\prime \prime}\) tiene un cero en\(S_{i}\). Que este cero sea denotado por\(\xi\), i.e\(\phi^{\prime \prime}(\xi)=0\).,. Evaluación de\(\phi^{\prime \prime}(\xi)\) rendimientos\[0=\phi^{\prime \prime}(\xi)=f^{\prime \prime}(\xi)-q^{\prime \prime}(\xi)=f^{\prime \prime}(\xi)-(\mathcal{I} f)^{\prime \prime}(\xi)-\lambda w^{\prime \prime}(\xi)=f^{\prime \prime}(\xi)-2 \lambda \quad \Rightarrow \quad \lambda=\frac{1}{2} f^{\prime \prime}(\xi) .\] Evaluando\(\phi(\hat{x})\), obtenemos\[\begin{aligned} 0 &=\phi(\hat{x})=f(\hat{x})-(\mathcal{I} f)(\hat{x})-\frac{1}{2} f^{\prime \prime}(\xi) w(\hat{x}) \\ f(\hat{x})-(\mathcal{I} f)(\hat{x}) &=\frac{1}{2} f^{\prime \prime}(\xi)\left(\hat{x}-\bar{x}^{1}\right)\left(\hat{x}-\bar{x}^{2}\right) . \end{aligned}\] La función se maximiza para\(\hat{x}^{*}=\left(\bar{x}^{1}+\bar{x}^{2}\right) / 2\), cual rinde\[f(\hat{x})-(\mathcal{I} f)(\hat{x}) \leq \frac{1}{8} f^{\prime \prime}(\xi)\left(\bar{x}^{2}-\bar{x}^{1}\right)^{2}=\frac{1}{8} h^{2} f^{\prime \prime}(\xi), \quad \forall \hat{x} \in\left[\bar{x}^{1}, \bar{x}^{2}\right]\] Desde\(\xi \in S_{i}\), se deduce que,\[e_{i}=\max _{x \in S_{i}}|f(x)-(\mathcal{I} f)(x)| \leq \frac{1}{8} h^{2} f^{\prime \prime}(\xi) \leq \frac{1}{8} h^{2} \max _{x \in S_{i}}\left|f^{\prime \prime}(x)\right| .\]

Ejemplo 2.1.5 cuadrático en forma de pieza

Motivados por la mayor precisión proporcionada por los interpolantes precisos y lineales de segundo orden, ahora consideramos usar un polinomio cuadrático por tramos para construir un interpolante. Debido a que una función cuadrática se caracteriza por tres parámetros, se requieren tres puntos de interpolación por segmento\((M=3)\). Para segmento\(S_{i}=\left[x_{i}, x_{i+1}\right]\), una elección natural son los dos puntos finales y el punto medio, es decir,\[\bar{x}^{1}=x_{i}, \quad \bar{x}^{2}=\frac{1}{2}\left(x_{i}+x_{i+1}\right), \quad \text { and } \quad \bar{x}^{3}=x_{i+1} .\] Para construir el interpolante, primero construimos polinomio base Lagrange de la forma\[\phi_{1}(x)=\frac{\left(x-\bar{x}^{2}\right)\left(x-\bar{x}^{3}\right)}{\left(\bar{x}^{1}-\bar{x}^{2}\right)\left(\bar{x}^{1}-\bar{x}^{3}\right)}, \quad \phi_{2}(x)=\frac{\left(x-\bar{x}^{1}\right)\left(x-\bar{x}^{3}\right)}{\left(\bar{x}^{2}-\bar{x}^{1}\right)\left(\bar{x}^{2}-\bar{x}^{3}\right)}, \quad \text { and } \quad \phi_{3}(x)=\frac{\left(x-\bar{x}^{1}\right)\left(x-\bar{x}^{2}\right)}{\left(\bar{x}^{3}-\bar{x}^{1}\right)\left(\bar{x}^{3}-\bar{x}^{2}\right)} .\] Por construcción,\(\phi_{1}\) toma el valor de 1 at\(\bar{x}^{1}\) y desaparece en\(\bar{x}^{2}\) y\(\bar{x}^{3}\). Más generalmente, la base Lagrange tiene la propiedad\[\phi_{m}\left(\bar{x}^{n}\right)=\left\{\begin{array}{ll} 1, & n=m \\ 0, & n \neq m \end{array} .\right.\] Usando estas funciones base, podemos construir el interpolante cuadrático como\[(\mathcal{I} f)(x)=f\left(\bar{x}^{1}\right) \phi_{1}(x)+f\left(\bar{x}^{2}\right) \phi_{2}(x)+f\left(\bar{x}^{3}\right) \phi_{3}(x), \quad \forall x \in S_{i} .\]

(a) interpolante

(b) error

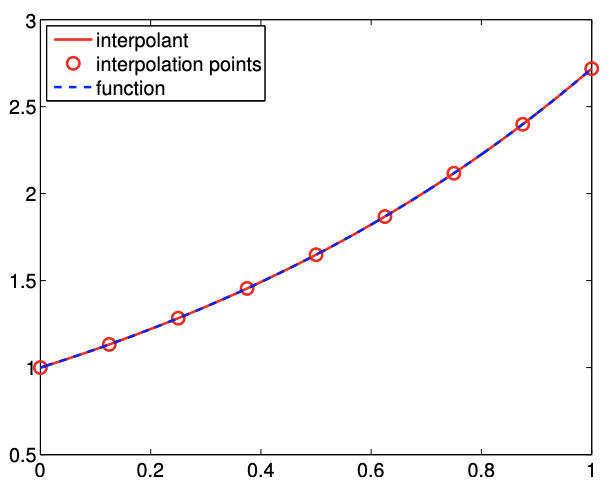
Figura 2.11: Interpolante cuadrático por tramos.

Podemos confirmar fácilmente que la función cuadrática pasa por los puntos de interpolación,\(\left(\bar{x}^{m}, f\left(\bar{x}^{m}\right)\right)\),\(m=1,2,3\), usando la propiedad de la base Lagrange. La Figura 2.11 (a) muestra el interpolante para la función exponencial.

Si\(f^{\prime \prime \prime}\) existe, el error del interpolante cuadrático está limitado por\[e_{i} \leq \frac{h^{3}}{72 \sqrt{3}} \max _{x \in S_{i}} f^{\prime \prime \prime}(x) .\] El error converge como la potencia cúbica de\(h\), lo que significa que el esquema es preciso de tercer orden. La figura\(2.11\) (b) confirma la convergencia de orden superior del interpolante cuadrático-fragmentado.

Prueba

La prueba es una extensión de eso para el interpolante lineal. Primero, formamos un interpolante cúbico de la forma\[q(x) \equiv(\mathcal{I} f)(x)+\lambda w(x) \quad \text { with } \quad w(x)=\left(x-\bar{x}^{1}\right)\left(x-\bar{x}^{2}\right)\left(x-\bar{x}^{3}\right) .\] Seleccionamos\(\lambda\) tal que\(q\) coincida\(f\) en\(\hat{x}\). La función de error de interpolación,\[\phi(x)=f(x)-q(x),\] tiene cuatro ceros en\(S_{i}\), específicamente\(\bar{x}^{1}, \bar{x}^{2}, \bar{x}^{3}\), y\(\hat{x}\). Al aplicar repetidamente el teorema de Rolle tres veces, observamos que\(\phi^{\prime \prime \prime}(x)\) tiene un cero adentro\(S_{i}\). Denotemos este cero por\(\xi\), es decir,\(\phi^{\prime \prime \prime}(\xi)=0\). Esto implica que\[\phi^{\prime \prime \prime}(\xi)=f^{\prime \prime \prime}(\xi)-(c I f)^{\prime \prime \prime}(\xi)-\lambda w^{\prime \prime \prime}(\xi)=f^{\prime \prime \prime}(\xi)-6 \lambda=0 \quad \Rightarrow \quad \lambda=\frac{1}{6} f^{\prime \prime \prime}(\xi) .\] Reordenando la expresión para\(\phi(\hat{x})\), obtenemos\[f(\hat{x})-(\mathcal{I} f)(\hat{x})=\frac{1}{6} f^{\prime \prime \prime}(\xi) w(\hat{x}) .\]

(a) interpolante

(b) error

Figura 2.12: Interpolante cuadrático por tramos para una función no suave.

El valor máximo que\(w\) se hace cargo\(S_{i}\) es\(h^{3} /(12 \sqrt{3})\). Combinado con el hecho\(f^{\prime \prime \prime}(\xi) \leq\)\(\max _{x \in S_{i}} f^{\prime \prime \prime}(x)\), obtenemos el límite de error\[e_{i}=\max _{x \in S_{i}}|f(x)-(\mathcal{I} f)(x)| \leq \frac{h^{3}}{72 \sqrt{3}} \max _{x \in S_{i}} f^{\prime \prime \prime}(x) .\] Note que la extensión de esta prueba a interpolantes de orden superior es sencilla. En general, un interpolante polinomio de\(p^{\text {th }}\) grados por tramos exhibe convergencia de\(p+1\) orden.

El procedimiento para construir los polinomios de Lagrange se extiende a polinomios de grado arbitrario. Así, en principio, podemos construir un interpolante arbitrariamente de alto orden aumentando el número de puntos de interpolación. Mientras que la interpolación de orden superior produjo un error de interpolación menor para la función suave considerada, algunas precauciones están en orden.

Primero, los interpolantes de orden superior son más susceptibles a errores de modelado. Si los datos subyacentes son ruidosos, el “sobreajuste” de los datos ruidosos puede conducir a interpolantes inexactos. Esto se discutirá con más detalle en la Unidad III sobre regresión.

En segundo lugar, los interpolantes de orden superior tampoco suelen ser ventajosos para funciones no suaves. Para ver esto, volvemos a visitar la función discontinua simple,\[f(x)=\left\{\begin{array}{ll} \sin (\pi x), & x \leq \frac{1}{3} \\ \frac{1}{2} \sin (\pi x), & x>\frac{1}{3} \end{array} .\right.\] El resultado de aplicar la regla de interpolación cuadrática por partes a la función se muestra en la Figura\(2.12(\mathrm{a})\). El interpolante cuadrático coincide estrechamente con la función subyacente en la región suave. Sin embargo, en el tercer segmento, que contiene la discontinuidad, el interpolante difiere considerablemente de la función subyacente. Similar a la interpolación constante por partes de la función, nuevamente cometemos\(\mathcal{O}(1)\) error medido en la diferencia máxima. La Figura\(2.12\) (b) confirma que los interpolantes de orden superior no funcionan mejor que el interpolante constante por partes en presencia de discontinuidad. Formalmente, podemos demostrar que la convergencia de error máximo de cualquier esquema de interpolación no puede ser mejor que\(h^{r}\), donde\(r\) está la derivada de orden más alto que se define en todas partes del dominio. En presencia de una discontinuidad,\(r=0\), y observamos\(\mathcal{O}\left(h^{r}\right)=\mathcal{O}(1)\) convergencia (es decir, no convergencia).

Tercero, para un polinomio de orden muy alto, los puntos de interpolación deben elegirse cuidadosamente para lograr un buen resultado. En particular, la distribución uniforme sufre del comportamiento conocido como fenómeno de Runge, donde el interpolante exhibe una oscilación excesiva incluso si la función subyacente es suave. La oscilación espuria se puede minimizar agrupando los puntos de interpolación cerca de los puntos finales del segmento, por ejemplo, nodos de Chebyshev.

Material Avanzado

Interpolación: Polinomios de Grado\(n\)

Estudiaremos con más detalle cómo la elección de los puntos de interpolación afecta la calidad de un interpolante polinomial. Para mayor comodidad, denotemos el espacio\(n^{\mathrm{th}}\) de polinomios de grado en segmento\(S\) por\(\mathcal{P}_{n}(S)\). Para la consistencia, denotaremos interpolante polinomio de\(n^{\text {th }}\) -grado de\(f\), que se define por puntos de\(n+1\) interpolación\(\left\{\bar{x}^{m}\right\}_{m=1}^{n+1}\), por\(\mathcal{I}_{n} f\). Compararemos la calidad del interpolante con el polinomio de “mejor”\(n+1\) grado. Definiremos “mejor” en la norma del infinito, es decir, el mejor polinomio\(v^{*} \in \mathcal{P}_{n}(S)\) satisface\[\max _{x \in S}\left|f(x)-v^{*}(x)\right| \leq \max _{x \in S}|f(x)-v(x)|, \quad \forall v \in \mathcal{P}_{n}(x) .\] En cierto sentido, el polinomio\(v^{*}\) ajusta la función lo más cerca\(f\) posible. Entonces, la calidad\(n^{\text {th }}\) de un interpolante de grado se puede evaluar midiendo qué tan cerca está de\(v^{*}\). Más precisamente, cuantificamos su calidad comparando el error máximo del interpolante con el del mejor polinomio, es decir,\[\max _{x \in S}|f(x)-(\mathcal{I} f)(x)| \leq\left(1+\Lambda\left(\left\{\bar{x}^{m}\right\}_{m=1}^{n+1}\right)\right) \max _{x \in S}\left|f(x)-v^{*}(x)\right|,\] donde la constante\(\Lambda\) se llama constante de Lebesgue. Claramente, una constante de Lebesgue menor implica menor error, por lo que mayor es la calidad del interpolante. Al mismo tiempo,\(\Lambda \geq 0\) porque el error máximo en el interpolante no puede ser mejor que el de la “mejor” función, que por definición minimiza el error máximo. De hecho, la constante de Lebesgue viene dada por\[\Lambda\left(\left\{\bar{x}^{m}\right\}_{m=1}^{n+1}\right)=\max _{x \in S} \sum_{m=1}^{n+1}\left|\phi_{m}(x)\right|,\] donde\(\phi_{m}, m=1, \ldots, n+1\), son las funciones de bases de Lagrange definidas por los nodos\(\left\{\bar{x}^{m}\right\}_{m=1}^{n+1}\).

Prueba. Primero expresamos el error de interpolación en la norma del infinito como la suma de dos contribuciones\[\begin{aligned} \max _{x \in S}|f(x)-(\mathcal{I} f)(x)| & \leq \max _{x \in S}\left|f(x)-v^{*}(x)+v^{*}(x)-(\mathcal{I} f)(x)\right| \\ & \leq \max _{x \in S}\left|f(x)-v^{*}(x)\right|+\max _{x \in S}\left|v^{*}(x)-(\mathcal{I} f)(x)\right| . \end{aligned}\] Observando que las funciones en el segundo término son polinomios, las expresamos en términos de la base Lagrange\(\phi_{m}, m=1, \ldots, n\),\[\begin{aligned} \max _{x \in S}\left|v^{*}(x)-(\mathcal{I} f)(x)\right| &=\max _{x \in S}\left|\sum_{m=1}^{n+1}\left(v^{*}\left(\bar{x}^{m}\right)-(\mathcal{I} f)\left(\bar{x}^{m}\right)\right) \phi_{m}(x)\right| \\ & \leq \max _{x \in S}\left|\max _{m=1, \ldots, n+1}\right| v^{*}\left(\bar{x}^{m}\right)-(\mathcal{I} f)\left(\bar{x}^{m}\right)\left|\cdot \sum_{m=1}^{n+1}\right| \phi_{m}(x)|| \\ &=\max _{m=1, \ldots, n+1}\left|v^{*}\left(\bar{x}^{m}\right)-(\mathcal{I} f)\left(\bar{x}^{m}\right)\right| \cdot \max _{x \in S} \sum_{m=1}^{n+1}\left|\phi_{m}(x)\right| . \end{aligned}\] Porque\(\mathcal{I} f\) es un interpolante, nosotros tener\(f\left(\bar{x}^{m}\right)=(\mathcal{I} f)\left(\bar{x}^{m}\right), m=1, \ldots, n+1\). Además, reconocemos que el segundo término es la expresión de la constante de Lebesgue. Así, tenemos\[\begin{aligned} \max _{x \in S}\left|v^{*}(x)-(\mathcal{I} f)(x)\right| & \leq \max _{m=1, \ldots, n+1}\left|v^{*}\left(\bar{x}^{m}\right)-f\left(\bar{x}^{m}\right)\right| \cdot \Lambda \\ & \leq \max _{x \in S}\left|v^{*}(x)-f(x)\right| \Lambda . \end{aligned}\] donde la última desigualdad se deriva del reconocimiento\(\bar{x}^{m} \in S, m=1, \ldots, n+1\). Así, el error de interpolación en la norma máxima está limitado por\[\begin{aligned} \max _{x \in S}|f(x)-(\mathcal{I} f)(x)| & \leq \max _{x \in S}\left|v^{*}(x)-f(x)\right|+\max _{x \in S}\left|v^{*}(x)-f(x)\right| \Lambda \\ & \leq(1+\Lambda) \max _{x \in S}\left|v^{*}(x)-f(x)\right|, \end{aligned}\] lo que es el resultado deseado.

En la sección anterior, señalamos que los puntos igualmente espaciados pueden producir interpolantes inestables para un gran\(n\). De hecho, la constante de Lebesgue para la distribución de nodos igualmente espaciados varía ya que\[\Lambda \sim \frac{2^{n}}{e n \log (n)},\] es decir, la constante de Lebesgue aumenta exponencialmente con\(n\). Por lo tanto, aumentar\(n\) no es necesario dar como resultado un error de interpolación menor.

Se puede formar un interpolante más estable usando la distribución de nodos de Chebyshev. La distribución de nodos se da (on\([-1,1])\) by\[\bar{x}^{m}=\cos \left(\frac{2 m-1}{2(n+1)} \pi\right), \quad m=1, \ldots, n+1 .\] Note que los nodos están agrupados hacia los puntos finales. La constante de Lebesgue para la distribución de nodos de Chebyshev es\[\Lambda=1+\frac{2}{\pi} \log (n+1),\] decir, la constante crece mucho más lentamente. La variación en la constante de Lebesgue para las distribuciones de nodos igualmente espaciados y Chebyshev se muestran en la Figura\(\underline{2.13}\).

Figura 2.13: Constantes de Lebesgue aproximadas para distribuciones de nodos igualmente espaciados y Chebyshev.

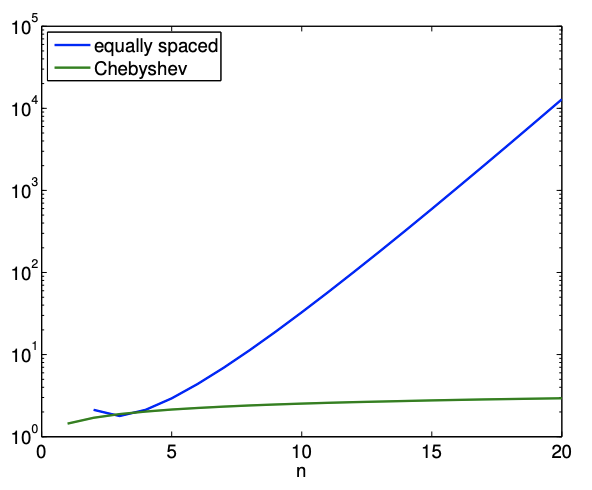
(a) equiespaciados

b) Distribución de Chebyshev

Figura 2.14: Interpolantes de orden\(f=1 /\left(x+25 x^{2}\right)\) superior para más\([-1,1]\).

Ejemplo 2.1.6 Fenómeno de Runge

Para demostrar la inestabilidad de los interpolantes basados en nodos igualmente espaciados, consideremos la interpolación de\[f(x)=\frac{1}{1+25 x^{2}}\] Los interpolantes resultantes para\(p=5,7\), y 11 se muestran en la Figura 2.14. Tenga en cuenta que los nodos equidistantes producen oscilaciones espurias cerca del final de los intervalos. Por otro lado, la agrupación de los nodos hacia los puntos finales permite que la distribución de nodos de Chebyshev controle el error en la región.

Material Avanzado

(a) malla

b) triángulo\(R_{i}\)

Figura 2.15: Triangulación de un dominio 2-D.