2.2: Interpolación de Funciones Bivariadas

Esta sección considera la interpolación de funciones bivariadas, es decir, funciones de dos variables. Siguiendo el enfoque adoptado en la construcción de interpolantes para funciones univariadas, primero discretizamos el dominio en regiones más pequeñas, a saber, triángulos. El proceso de descomponer un dominio,\(D \subset \mathbb{R}^{2}\), en un conjunto de triángulos no superpuestos\(\left\{R_{i}\right\}_{i=1}^{N}\) se denomina triangulación. Un ejemplo de triangulación se muestra en la Figura 2.15. Por construcción, los triángulos llenan el dominio en el sentido de que\[D=\bigcup_{i=1}^{N} \bar{R}_{i},\] donde\(\cup\) denota la unión de los triángulos. La triangulación se caracteriza por el tamaño\(h\), que es el diámetro máximo de los círculos circunscritos para los triángulos.

Figura 2.16: Función\(f(x, y)=\sin (\pi x) \sin (\pi y)\)

Para los dos siguientes ejemplos, consideramos la interpolación de la función bivariada\[f(x, y)=\sin (\pi x) \sin (\pi y), \quad(x, y) \in[0,1]^{2} .\] La función se muestra en la Figura\(\underline{2.16}\).

Ejemplo 2.2.1 Constante por pieza, centroide

El primer interpolante aproxima la función\(f\) por una función constante por tramos. Para construir una función constante en\(R\), necesitamos solo un punto de interpolación, es decir,\(M=1\). Escojamos el centroide del triángulo para que sea el punto de interpolación,\[\overline{\boldsymbol{x}}^{\mathbf{1}}=\frac{1}{3}\left(\boldsymbol{x}_{1}+\boldsymbol{x}_{2}+\boldsymbol{x}_{3}\right) .\] El interpolante constante viene dado por\[\mathcal{I} f(\boldsymbol{x})=f\left(\overline{\boldsymbol{x}}^{1}\right), \quad \forall \boldsymbol{x} \in R .\] Un ejemplo de interpolante constante por trozos se muestra en la Figura 2.17 (a). Tenga en cuenta que el interpolante es discontinuo a través de las interfaces triangulares en general.

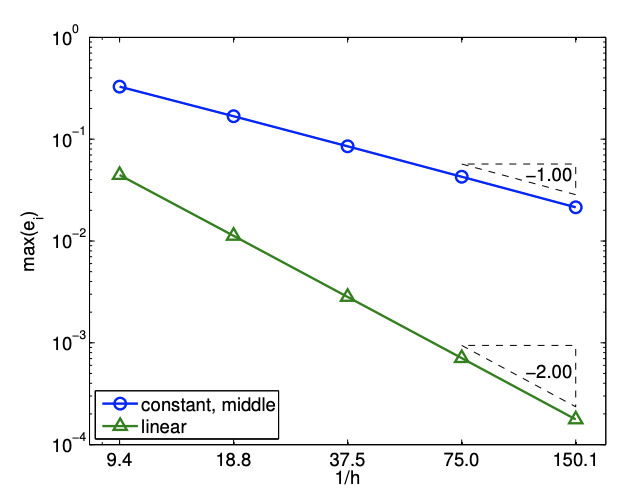
El error en el interpolante está limitado por\[e \leq h \max _{\boldsymbol{x} \in R}\|\nabla f(\boldsymbol{x})\|_{2},\] donde\(\|\nabla f(\boldsymbol{x})\|_{2}\) está la norma de dos del gradiente, es decir\[\|\nabla f\|_{2}=\sqrt{\left(\frac{\partial f}{\partial x}\right)^{2}+\left(\frac{\partial f}{\partial y}\right)^{2}} .\] El interpolante es preciso de primer orden y es exacto si\(f\) es constante. La figura 2.17 (b) confirma la\(h^{1}\) convergencia del error.

Ejemplo 2.2.2 Lineales por tramos, vértices

Este interpolante aproxima la función\(f\) por una función lineal por tramos. Tenga en cuenta que una función lineal en dos dimensiones se caracteriza por tres parámetros. Por lo tanto, para construir una función lineal en un

(a) interpolante

(b) error

Figura 2.17: Interpolación de constante a destajo

parche triangular\(R\), necesitamos elegir tres puntos de interpolación, es decir,\(M=3\). Escojamos los vértices del triángulo para que sean el punto de interpolación,\[\overline{\boldsymbol{x}}^{1}=\boldsymbol{x}_{1}, \quad \overline{\boldsymbol{x}}^{2}=\boldsymbol{x}_{2}, \quad \text { and } \quad \overline{\boldsymbol{x}}^{3}=\boldsymbol{x}_{3}\] El interpolante lineal es de la forma\[(\mathcal{I} f)(\boldsymbol{x})=a+b x+c y\] Para encontrar los tres parámetros,, y\(a, b\)\(c\), imponemos la restricción de que el interpolante coincida con el valor de la función en los tres vértices. La restricción da como resultado un sistema de tres ecuaciones lineales\[\begin{aligned} &(\mathcal{I} f)\left(\overline{\boldsymbol{x}}^{1}\right)=a+b \bar{x}^{1}+c \bar{y}^{1}=f\left(\overline{\boldsymbol{x}}^{1}\right) \\ &(\mathcal{I} f)\left(\overline{\boldsymbol{x}}^{2}\right)=a+b \bar{x}^{2}+c \bar{y}^{2}=f\left(\overline{\boldsymbol{x}}^{2}\right) \\ &(\mathcal{I} f)\left(\overline{\boldsymbol{x}}^{3}\right)=a+b \bar{x}^{3}+c \bar{y}^{3}=f\left(\overline{\boldsymbol{x}}^{3}\right) \end{aligned}\] que también se pueden escribir de manera concisa en forma de matriz.\[\left(\begin{array}{lll} 1 & \bar{x}^{1} & \bar{y}^{1} \\ 1 & \bar{x}^{2} & \bar{y}^{2} \\ 1 & \bar{x}^{3} & \bar{y}^{3} \end{array}\right)\left(\begin{array}{l} a \\ b \\ c \end{array}\right)=\left(\begin{array}{l} f\left(\bar{x}^{1}\right) \\ f\left(\bar{x}^{2}\right) \\ f\left(\bar{x}^{3}\right) \end{array}\right)\] El interpolante resultante se muestra en la Figura\(2.18(\mathrm{a})\). A diferencia del interpolante constante por tramos, el interpolante lineal por tramos es continuo a través de las interfaces triangulares.

El enfoque para construir la interpolación lineal requiere resolver un sistema de tres ecuaciones lineales. Un enfoque alternativo más eficiente es considerar una forma diferente del interpolante. A saber, consideramos que la forma\[(\mathcal{I} f)(\boldsymbol{x})=f\left(\bar{x}^{1}\right)+b^{\prime}\left(x-\bar{x}^{1}\right)+c^{\prime}\left(y-\bar{y}^{1}\right)\]

(a) interpolante

(b) error

Figura 2.18: Interpolación lineal por tramos

Obsérvese que el interpolante sigue siendo lineal, pero ya satisface la condición de interpolación en\(\left(\overline{\boldsymbol{x}}^{1}, f\left(\overline{\boldsymbol{x}}^{1}\right)\right)\) porque\[(\mathcal{I} f)\left(\overline{\boldsymbol{x}}^{1}\right)=f\left(\overline{\boldsymbol{x}}^{1}\right)+b^{\prime}\left(\bar{x}^{1}-\bar{x}^{1}\right)+c^{\prime}\left(\bar{y}^{1}-\bar{y}^{1}\right)=f\left(\overline{\boldsymbol{x}}^{1}\right)\] Así, nuestra tarea se ha simplificado a la de encontrar los dos coeficientes\(b^{\prime}\) y\(c^{\prime}\), como oponerse a los tres coeficientes \(a, b\), y\(c\). Elegimos los dos coeficientes de tal manera que el interpolante satisfaga la condición de interpolación en\(\overline{\boldsymbol{x}}^{2}\) y\(\overline{\boldsymbol{x}}^{3}\), es decir\[\begin{aligned} &(\mathcal{I} f)\left(\bar{x}^{2}\right)=f\left(\bar{x}^{1}\right)+b^{\prime}\left(\bar{x}^{2}-\bar{x}^{1}\right)+c^{\prime}\left(\bar{y}^{2}-\bar{y}^{1}\right)=f\left(\bar{x}^{2}\right) \\ &(\mathcal{I} f)\left(\bar{x}^{3}\right)=f\left(\bar{x}^{1}\right)+b^{\prime}\left(\bar{x}^{3}-\bar{x}^{1}\right)+c^{\prime}\left(\bar{y}^{3}-\bar{y}^{1}\right)=f\left(\bar{x}^{3}\right) \end{aligned}\] O, de manera más compacta, podemos escribir las ecuaciones en forma de matriz como\[\left(\begin{array}{cc} \bar{x}^{2}-\bar{x}^{1} & \bar{y}^{2}-\bar{y}^{1} \\ \bar{x}^{3}-\bar{x}^{1} & \bar{y}^{3}-\bar{y}^{1} \end{array}\right)\left(\begin{array}{c} b^{\prime} \\ c^{\prime} \end{array}\right)=\left(\begin{array}{c} f\left(\overline{\boldsymbol{x}}^{2}\right)-f\left(\overline{\boldsymbol{x}}^{1}\right) \\ f\left(\overline{\boldsymbol{x}}^{3}\right)-f\left(\overline{\boldsymbol{x}}^{1}\right) \end{array}\right)\] Con algunas aritméticas, podemos encontrar una forma explícita de la coeficientes,\[\begin{aligned} b^{\prime} &=\frac{1}{A}\left[\left(f\left(\bar{x}^{2}\right)-f\left(\bar{x}^{1}\right)\right)\left(\bar{y}^{3}-\bar{y}^{1}\right)-\left(f\left(\bar{x}^{3}\right)-f\left(\bar{x}^{1}\right)\right)\left(\bar{y}^{2}-\bar{y}^{1}\right)\right] \\ c^{\prime} &=\frac{1}{A}\left[\left(f\left(\bar{x}^{3}\right)-f\left(\bar{x}^{1}\right)\right)\left(\bar{x}^{2}-\bar{x}^{1}\right)-\left(f\left(\bar{x}^{2}\right)-f\left(\bar{x}^{1}\right)\right)\left(\bar{x}^{3}-\bar{x}^{1}\right)\right] \end{aligned}\] con\[A=\left(\bar{x}^{2}-\bar{x}^{1}\right)\left(\bar{y}^{3}-\bar{y}^{1}\right)-\left(\bar{x}^{3}-\bar{x}^{1}\right)\left(\bar{y}^{2}-\bar{y}^{1}\right)\] Note que\(A\) es el doble del área del triángulo. Es importante señalar que esta segunda forma del interpolante lineal es idéntica a la primera forma; el interpolante solo se expresa en una forma diferente. El error en el interpolante está gobernado por el hessiano de la función, es decir,\[e \leq C h^{2}\left\|\nabla^{2} f\right\|_{F},\] dónde\(\left\|\nabla^{2} f\right\|_{F}\) está la norma Frobenius de la matriz hessiana, es decir,\[\left\|\nabla^{2} f\right\|_{F}=\sqrt{\left(\frac{\partial^{2} f}{\partial x^{2}}\right)^{2}+\left(\frac{\partial^{2} f}{\partial y^{2}}\right)^{2}+2\left(\frac{\partial^{2} f}{\partial x \partial y}\right)^{2}} .\] por lo tanto, el interpolante lineal por tramos es preciso de segundo orden y es exacto si\(f\) es lineal. El resultado de convergencia mostrado en la Figura 2.18 (b) confirma la\(h^{2}\) convergencia del error.