7.1: Integración de Funciones Univariadas

Nuestro objetivo es aproximar el valor de la integral\[ I=\int_{a}^{b} f(x) d x,\] para alguna función univariada arbitraria\(f(x)\). Nuestro enfoque de este problema de integración es aproximar la función\(f\) por un interpolante\(\mathcal{I} f\) e integrar exactamente el interpolante, es decir,\[\tag{7.1} I=\sum_{i=1}^{N-1} \int_{S_{i}} f(x) d x \approx \sum_{i=1}^{N-1} \int_{S_{i}}(\mathcal{I} f)(x) d x \equiv I_{h}\] Recordemos que al construir un interpolante, discretizamos el dominio\([a, b]\) en \(N-1\)segmentos no superpuestos, delineados por puntos de segmentación\(x_{i}, i=1, \ldots, N\), como se ilustra en la Figura\(7.1^{1}\) Entonces, construimos un interpolante polinómico en cada segmento utilizando los valores de función en los puntos de interpolación locales,\(\bar{x}^{m}, m=1, \ldots, M\). Estos puntos de interpolación local se pueden mapear a puntos de evaluación de funciones globales,\(\tilde{x}_{i}, i=1, \ldots, N_{\text {eval }}\). La calidad del interpolante viene dictada por su tipo y la longitud del segmento\(h\), que a su vez gobierna la calidad de la aproximación integral,\(I_{h}\). El subíndice\(h\) encendido\(I_{h}\) significa que la integración se realiza en una discretización con una longitud de segmento\(h\). Este proceso de integración aprovecha la facilidad de integrar el interpolante polinomial en cada segmento.

Recordando que el error en la interpolación disminuye con\(h\), podemos esperar que la aproximación de la integral se\(I_{h}\) acerque a la verdadera integral\(I\) como\(h\) va a 0. Establezcamos formalmente la relación entre el límite de error de interpolación\(e_{\max }=\max _{i} e_{i}\), y el error de integración,

\({ }^{1}\)Por simplicidad, asumimos que\(h\) es constante en todo el dominio.

Figura 7.1: Discretización de un dominio 1d en\(N-1\) (aquí\(N=5\)) segmentos de longitud\(h\).

\(\left|I-I_{h}\right| .\)\[\begin{aligned} \left|I-I_{h}\right| &=\left|\sum_{i=1}^{N-1} \int_{S_{i}}(f(x)-(\mathcal{I} f)(x)) d x\right| \\ & \leq\left|\sum_{i=1}^{N-1} \int_{S_{i}}\right| f(x)-(\mathcal{I} f)(x)|d x| \\ & \leq\left|\sum_{i=1}^{N-1} \int_{S_{i}} e_{i} d x\right| \\ & \leq \sum_{i=1}^{N-1} e_{i} h \\ & \leq e_{\max } \sum_{i=1}^{N-1} h \\ &=(b-a) e_{\max } . \end{aligned}\]\[\begin{aligned} & \begin{aligned}&\leq \sum_{i=1} \int_{S_{i}} e_{i} d x \mid \\&\leq \sum_{i=1}^{N-1} e_{i} h \quad \text { (definition of } h \text { ) }\end{aligned} \end{aligned}\](definición de\(e_{\max }\))

Hacemos algunas observaciones. En primer lugar, el error global en la integral es una suma de las contribuciones de error local. Segundo, dado que todos los esquemas de interpolación considerados en la Sección\(2.1\) son convergentes\(\left(e_{\max } \rightarrow 0\right.\) como\(\left.h \rightarrow 0\right)\), el error de integración también desaparece a medida que\(h\) va a cero. En tercer lugar, si bien este límite se aplica a cualquier esquema de integración basado en interpolación, el límite no es nítido; es decir, algunos esquemas de integración mostrarían una mejor convergencia con la\(h\) que predice la teoría.

Recordemos que la construcción de un interpolante particular solo depende de la ubicación de los puntos de interpolación y los valores de función asociados\(\left(\tilde{x}_{i}, f\left(\tilde{x}_{i}\right)\right), i=1, \ldots, N_{\mathrm{eval}}\), donde\(N_{\text {eval }}\) está el número de los puntos de evaluación de la función (global). Como resultado, las reglas de integración basadas en el interpolante también solo dependen de los valores de la función en estos\(N_{\text {eval }}\) puntos. Específicamente, todas las reglas de integración consideradas en este capítulo son de la forma\[I_{h}=\sum_{i=1}^{N_{\text {eval }}} w_{i} f\left(\tilde{x}_{i}\right),\] donde\(w_{i}\) están los pesos asociados a cada punto y son dependientes del interpolante a partir del cual se construyen las reglas de integración. En el contexto de la integración numérica, los puntos de evaluación de funciones se denominan puntos de cuadratura y los pesos asociados se denominan pesos en cuadratura. Los puntos de cuadratura y los pesos juntos constituyen una regla de cuadratura. No es muy sorprendente considerando la teoría de integración de Riemann, la integral se aproxima como una combinación lineal de los valores de la función en los puntos de cuadratura.

Demos varios ejemplos de reglas de integración.

Ejemplo 7.1.1 regla rectangular, izquierda

La primera regla de integración considerada es una regla rectangular basada en la regla de interpolación de punto izquierdo constante por partes considerada en el Ejemplo 2.1.1. Recordemos que el interpolante sobre cada segmento se obtiene aproximando el valor de la función por una función constante que coincide con el valor de la función en el punto final izquierdo, es decir, el punto de interpolación está\(\bar{x}^{1}=x_{i}\) en el segmento\(S_{i}=\left[x_{i}, x_{i+1}\right]\). La fórmula de integración resultante es\[I_{h}=\sum_{i=1}^{N-1} \int_{S_{i}}(\mathcal{I} f)(x) d x=\sum_{i=1}^{N-1} \int_{S_{i}} f\left(x_{i}\right) d x=\sum_{i=1}^{N-1} h f\left(x_{i}\right)\] donde la función constante por partes resulta en una integración trivial. Recordando que los puntos de evaluación de la función global\(\tilde{x}_{i}\),, están relacionados con los puntos de segmentación\(x_{i}\),, por también\[\tilde{x}_{i}=x_{i}, \quad i=1, \ldots, N-1,\] podemos expresar la regla de integración ya que la\[I_{h}=\sum_{i=1}^{N-1} h f\left(\tilde{x}_{i}\right) .\] Figura 7.2 (a) ilustra la regla de integración aplicada a\(f(x)=\exp (x)\) más \([0,1]\)con\(N=5\). Recordemos que por simplicidad asumimos que todos los intervalos son de la misma longitud,\(h \equiv x_{i+1}-x_{i}, i=1, \ldots, N-1\).

Analicemos ahora el error asociado a esta regla de integración. A partir de la figura, queda claro que el error en el integrando es una suma de los errores locales cometidos en cada segmento. El error local en cada segmento es el hueco triangular entre el interpolante y la función, que tiene la longitud\(h\) y la altura proporcional a\(f^{\prime} h\). Así, el error local escala como\(f^{\prime} h^{2}\). Ya que hay\((b-a) / h\) segmentos, esperamos que el error de integración global se escale como\[\left|I-I_{h}\right| \sim f^{\prime} h^{2}(b-a) / h \sim h f^{\prime} .\] Más formalmente, podemos aplicar el límite de error de integración general, Eq. (7.7), para obtener\[\left|I-I_{h}\right| \leq(b-a) e_{\max }=(b-a) h \max _{x \in[a, b]}\left|f^{\prime}(x)\right| .\] De hecho, este límite puede ser apretado por un factor constante, cediendo\[\left|I-I_{h}\right| \leq(b-a) \frac{h}{2} \max _{x \in[a, b]}\left|f^{\prime}(x)\right| .\]

(a) integral

(b) error

Figura 7.2: Rectángulo, regla de extremo izquierdo.

La Figura 7.2 (b) captura el comportamiento de convergencia del esquema aplicado a la función exponencial. Según lo predicho por la teoría, esta regla de integración es precisa de primer orden y las escalas de error como\(\mathcal{O}(h)\). Obsérvese también que la aproximación\(I_{h}\) subestima el valor de\(I\) si\(f^{\prime}>0\) sobre el dominio.

Antes de proceder a una prueba del agudo error encuadernado para un general\(f\), analicemos el error de integración directamente para una función lineal\(f(x)=m x+c\). En este caso, el error se puede expresar como\[\begin{aligned} \left|I-I_{h}\right| &=\sum_{i=1}^{N-1} \int_{S_{i}} f(x)-(\mathcal{I} f)(x) d x=\sum_{i=1}^{N-1} \int_{x_{i}}^{x_{i+1}}(m x-c)-\left(m x_{i}-c\right) d x \\ &=\sum_{i=1}^{N-1} \int_{x_{i}}^{x_{i+1}} m \cdot\left(x-x_{i}\right) d x=\sum_{i=1}^{N-1} \frac{1}{2} m\left(x_{i+1}-x_{i}\right)^{2} \\ &=\frac{1}{2} m h \sum_{i=1}^{N-1} h=\frac{1}{2} m h(b-a), \end{aligned}\] Note que la integral de\(m \cdot\left(x-x_{i}\right)\) over\(S_{i}\) es precisamente igual al área del triángulo faltante, con la base\(h\) y la altura\(m h\). Porque\(m=f^{\prime}(x), \forall x \in[a, b]\), confirmamos que el límite de error general es correcto, y de hecho agudo, para la función lineal. Demostremos ahora el resultado para un general\(f\).

Prueba

Por el teorema fundamental del cálculo, tenemos\[f(x)-(\mathcal{I} f)(x)=\int_{x_{i}}^{x} f^{\prime}(\xi) d \xi, \quad x \in S_{i}=\left[x_{i}, x_{i+1}\right]\] Integrando la expresión sobre segmento\(S_{i}\) y usando el Teorema del Valor Medio,\[\begin{aligned} \int_{S_{i}} f(x)-(\mathcal{I} f)(x) d x &=\int_{x_{i}}^{x_{i+1}} \int_{x_{i}}^{x} f^{\prime}(\xi) d \xi d x \\ &=\int_{x_{i}}^{x_{i+1}}\left(x-x_{i}\right) f^{\prime}(z) d x \\ & \leq \int_{x_{i}}^{x_{i+1}}\left|\left(x-x_{i}\right) f^{\prime}(z)\right| d x \\ & \leq\left(\int_{x_{i}}^{x_{i+1}}\left|x-x_{i}\right| d x\right) \max _{z \in\left[x_{i}, x_{i+1}\right]}\left|f^{\prime}(z)\right| \\ &=\frac{1}{2}\left(x_{i+1}-x_{i}\right)^{2} \max _{z \in\left[x_{i}, x_{i+1}\right]}\left|f^{\prime}(z)\right| \\ & \leq \frac{1}{2} h^{2} \max _{x \in\left[x_{i}, x_{i+1}\right]}\left|f^{\prime}(x)\right| . \end{aligned}\] (Teorema del Valor Medio, para algunos\(z \in\left[x_{i}, x\right]\))

Sumando las contribuciones locales al error integral,\ [\ izquierda|i-i_ {h}\ derecha|=\ izquierda|\ sum_ {i=1} ^ {N-1}\ int_ {S_ {i}} f (x) - (\ mathcal {I} f) (x) d x\ derecha|\ leq sum_ {i=1} ^ {N-1}\ frac {1} {2} h^ {2}\ max _ {x\ in\ izquierda [x_ {i}, x_ {i+1}\ derecha]}\ izquierda|f^ {\ prime} (x)\ derecha|\ leq (b-a)\ frac {h} {2}\ max _ {x\ in [a, b]}\ izquierda|f^ {\ prime} ( x)\ derecha|\

Ejemplo 7.1.2 regla rectangular, derecha

Esta regla de integración se basa en la regla de interpolación de punto final derecho, constante por partes, considerada en el Ejemplo 2.1.2, en la que el punto de interpolación se elige como\(\bar{x}^{1}=x_{i+1}\) en segmento\(S_{i}=\left[x_{i}, x_{i+1}\right]\). Esto da como resultado la fórmula de integración\[I_{h}=\sum_{i=1}^{N-1} \int_{S_{i}}(\mathcal{I} f)(x) d x=\sum_{i=1}^{N-1} \int_{S_{i}} f\left(x_{i+1}\right) d x=\sum_{i=1}^{N-1} h f\left(x_{i+1}\right) .\] Recordando que los puntos de evaluación de funciones globales están relacionados con los puntos de segmentación por\(\tilde{x}_{i}=x_{i+1}\)\(i=1, \ldots, N-1\),, también tenemos\[I_{h}=\sum_{i=1}^{N-1} h f\left(\tilde{x}_{i}\right) .\] Mientras que la forma de la ecuación es similar a la regla rectangular, izquierda, tenga en cuenta que la ubicación de los puntos de cuadratura\(\tilde{x}_{i}, i=1, \ldots, N-1\) son diferentes. El proceso de integración se ilustra en la Figura 7.1.2

Figura 7.3: Rectángulo, regla de punto final derecho.

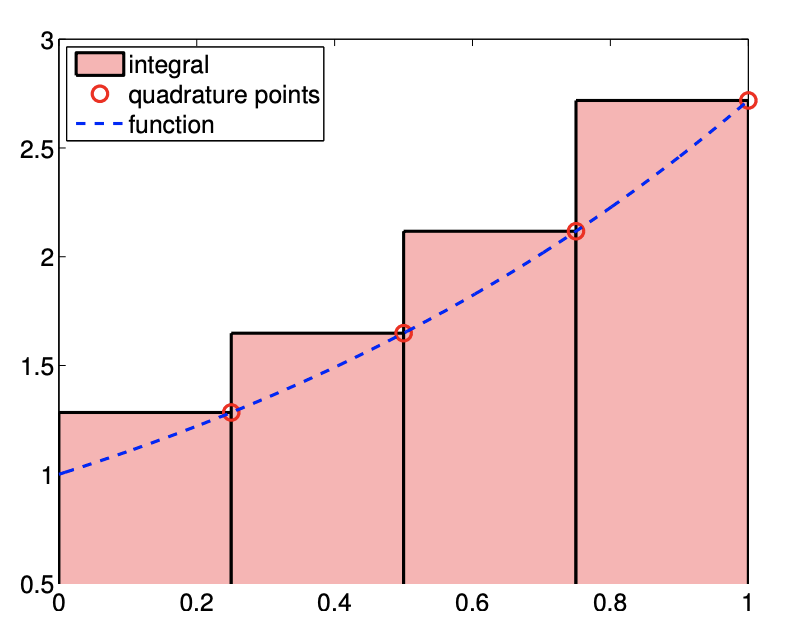
Esta regla es muy similar a la regla rectangular, izquierda. En particular, el error de integración está limitado por\[\left|I-I_{h}\right| \leq(b-a) \frac{h}{2} \max _{x \in[a, b]}\left|f^{\prime}(x)\right| .\] La expresión muestra que el esquema es preciso de primer orden, y la regla integra exactamente la función constante. Aunque los límites de error son idénticos, las reglas de rectángulo izquierdo y derecho en general dan diferentes aproximaciones. En particular, la regla de punto final derecho sobreestima\(I\) si está\(f^{\prime}>0\) sobre el dominio. La prueba del error encuadernado idéntico al de la regla del rectángulo izquierdo.

Si bien las reglas de rectángulo izquierdo y derecho son similares para integrar una función estática, exhiben propiedades fundamentalmente diferentes cuando se usan para integrar ecuaciones diferenciales ordinarias. En particular, las reglas de integración izquierda y derecha dan como resultado los esquemas hacia adelante y hacia atrás de Euler, respectivamente. Estos dos esquemas exhiben propiedades de estabilidad completamente diferentes, las cuales serán discutidas en capítulos sobre Ecuaciones Diferenciales Ordinarias.

Ejemplo 7.1.3 regla rectangular, punto medio

La tercera regla de integración considerada se basa en la regla de interpolación de punto medio, constante por partes, considerada en el Ejemplo 2.1.3. Eligiendo el punto medio\(\bar{x}^{1}=\left(x_{i}+x_{i+1}\right)\) como el punto de interpolación para cada uno\(S_{i}=\left[x_{i}, x_{i+1}\right]\), la fórmula de integración viene dada por\[I_{h}=\sum_{i=1}^{N-1} \int_{S_{i}}(\mathcal{I} f)(x) d x=\sum_{i=1}^{N-1} \int_{S_{i}} f\left(\frac{x_{i}+x_{i+1}}{2}\right) d x=\sum_{i=1}^{N-1} h f\left(\frac{x_{i}+x_{i+1}}{2}\right)\] Recordando que el punto de evaluación de función global de la interpolación de punto medio está relacionado con los puntos de segmentación por\(\tilde{x}_{i}=\left(x_{i}+x_{i+1}\right) / 2, i=1, \ldots, N-1\), regla de cuadratura también se puede expresar como\[\sum_{i=1}^{N-1} h f\left(\tilde{x}_{i}\right)\] El proceso de integración se ilustra en la Figura\(7.4(\mathrm{a}) .\)

(a) integral

(b) error

Figura 7.4: Rectángulo, regla de punto medio.

El análisis de errores para la regla del punto medio está más involucrado que el de los métodos anteriores. Si aplicamos el límite de error general, Ec. (7.7), junto con los límites de error de interpolación para la regla de punto medio, obtenemos el límite de error de\[\left|I-I_{h}\right| \leq(b-a) e_{\max } \leq(b-a) \frac{h}{2} \max _{x \in[a, b]}\left|f^{\prime}(x)\right|\] Sin embargo, este límite no es nítido. El límite de error agudo para el rectángulo, regla de integración de punto medio viene dado por\[\left|I-I_{h}\right| \leq \frac{1}{24}(b-a) h^{2} \max _{x \in[a, b]}\left|f^{\prime \prime}(x)\right|\] Así, la regla de rectángulo, punto medio es precisa de segundo orden. La mayor precisión y tasa de convergencia de la regla de punto medio se capturan en la gráfica de convergencia de error en la Figura\(7.4(\mathrm{~b})\).

Antes de probar el límite de error para un general\(f\), mostremos que la regla del rectángulo de hecho integra\(f(x)=m x+c\) exactamente una función lineal. El error de integración para una función lineal se puede expresar como\[\begin{aligned} I-I_{h} &=\sum_{i=1}^{N-1} \int_{S_{i}} f(x)-(\mathcal{I} f)(x) d x=\sum_{i=1}^{N-1} \int_{x_{i}}^{x_{i+1}} f(x)-f\left(\frac{x_{i}+x_{i+1}}{2}\right) d x \\ &=\sum_{i=1}^{N-1} \int_{x_{i}}^{x_{i+1}}(m x+c)-\left(m\left(\frac{x_{i}+x_{i+1}}{2}\right)+c\right) d x \\ &=\sum_{i=1}^{N-1} \int_{x_{i}}^{x_{i+1}} m\left[x-\frac{x_{i}+x_{i+1}}{2}\right] d x \end{aligned}\] Por conveniencia, denotemos el punto medio de integral por\(x_{c}\), es decir,\(x_{c}=\left(x_{i}+x_{i+1}\right) / 2\). Esto nos permite expresar los dos puntos finales como\(x_{i}=x_{c}-h / 2\) y\(x_{i+1}=x_{c}+h / 2\). Dividimos la integral segmentada en cada punto medio, rindiendo\[\begin{aligned} \int_{x_{i}}^{x_{i+1}} m\left[x-\frac{x_{i}+x_{i+1}}{2}\right] d x &=\int_{x_{c}-h / 2}^{x_{c}+h / 2} m\left(x-x_{c}\right) d x \\ &=\int_{x_{c}-h / 2}^{x_{c}} m\left(x-x_{c}\right) d x+\int_{x_{c}}^{x_{c}+h / 2} m\left(x-x_{c}\right) d x=0 . \end{aligned}\] La primera integral corresponde al área (firmada) de un triángulo con la base\(h / 2\) y la altura\(-m h / 2\). La segunda integral corresponde al área de un triángulo con la base\(h / 2\) y la altura\(m h / 2\). Así, la contribución de error de estos dos triángulos más pequeños se\(S_{i}\) cancelan entre sí, y la regla de punto medio integra exactamente la función lineal.

Prueba

Para mayor comodidad, denotemos el punto medio del segmento\(S_{i}\) por\(x_{m_{i}}\). La aproximación del punto medio de la integral sobre\(S_{i}\) es\[I_{h}^{n}=\int_{x_{i}}^{x_{i+1}} f\left(x_{m_{i}}\right) d x=\int_{x_{i}}^{x_{i+1}} f\left(x_{m_{i}}\right)+m\left(x-x_{m_{i}}\right) d x,\] para cualquiera\(m\). Tenga en cuenta que la adición de la función lineal con pendiente\(m\) que se desvanece en\(x_{m_{i}}\) no altera el valor de la integral. El error local en la aproximación es\[\left|I^{n}-I_{h}^{n}\right|=\left|\int_{x_{i}}^{x_{i+1}} f(x)-f\left(x_{m_{i}}\right)-m\left(x-x_{m_{i}}\right) d x\right| .\] Recall the Taylor series expansion,\[f(x)=f\left(x_{m_{i}}\right)+f^{\prime}\left(x_{m_{i}}\right)\left(x-x_{m_{i}}\right)+\frac{1}{2} f^{\prime \prime}\left(\xi_{i}\right)\left(x-x_{m_{i}}\right)^{2},\] para algunos\(\xi_{i} \in\left[x_{m_{i}}, x\right]\) (o\(\xi_{i} \in\left[x, x_{m, n}\right]\) si\(x<x_{m_{i}}\)). Sustitución de la serie Taylor representación\(f\) y\(m=f^{\prime}\left(x_{m_{i}}\right)\) rendimientos\[\begin{aligned} \left|I^{n}-I_{h}^{n}\right| &=\left|\int_{x_{i}}^{x_{i+1}} \frac{1}{2} f^{\prime \prime}\left(\xi_{i}\right)\left(x-x_{m_{i}}\right)^{2} d x\right| \leq \int_{x_{i}}^{x_{i+1}} \frac{1}{2}\left|f^{\prime \prime}\left(\xi_{i}\right)\left(x-x_{m_{i}}\right)^{2}\right| d x \\ & \leq\left(\int_{x_{i}}^{x_{i+1}} \frac{1}{2}\left(x-x_{m_{i}}\right)^{2} d x\right) \max _{\xi \in\left[x_{i}, x_{i+1}\right]}\left|f^{\prime \prime}(\xi)\right|=\left(\left.\frac{1}{6}\left(x-x_{m_{i}}\right)^{3}\right|_{x=x_{i}} ^{x_{i+1}}\right) \max _{\xi \in\left[x_{i}, x_{i+1}\right]}\left|f^{\prime \prime}(\xi)\right| \\ &=\frac{1}{24} h^{3} \max _{\xi \in\left[x_{i}, x_{i+1}\right]}\left|f^{\prime \prime}(\xi)\right| . \end{aligned}\] Sumando las contribuciones locales al error de integración, obtenemos\[\left|I-I_{h}\right| \leq \sum_{i=1}^{N-1} \frac{1}{24} h^{3} \max _{\xi_{i} \in\left[x_{i}, x_{i+1}\right]}\left|f^{\prime \prime}\left(\xi_{i}\right)\right| \leq \frac{1}{24}(b-a) h^{2} \max _{x \in[a, b]}\left|f^{\prime \prime}(x)\right| .\]

La regla rectángulo, punto medio pertenece a una familia de fórmulas de integración Newton-Cotes, las reglas de integración con puntos de evaluación equiespaciados. Sin embargo, este es también un ejemplo de cuadratura Gauss, que resulta de recoger pesos y ubicaciones de puntos para una precisión óptima. En particular, la cuadratura de Gauss\(k\) puntual logra la\(2 k\) convergencia de orden en una dimensión. La regla de punto medio es una cuadratura Gauss de un punto, logrando una precisión de segundo orden.

En el ejemplo anterior, mencionamos que la regla de punto medio -que exhibe convergencia de segundo orden usando solo un punto de cuadratura- es un ejemplo de reglas de cuadratura de Gauss. Las reglas de cuadratura de Gauss se obtienen eligiendo tanto los puntos de cuadratura como los pesos de manera “óptima”. Esto contrasta con las reglas de Newton-Cotes (por ejemplo, regla trapezoidal), que se basa en puntos igualmente espaciados. La regla “óptima” se refiere a la regla que maximiza el grado de polinomio integrado exactamente para un número dado de puntos. En una dimensión, la cuadratura de Gauss\(n\) -punto integra el polinomio\(2 n-1\) grado exactamente. Esto puede no ser demasiado sorprendente porque\(2 n-1\) grado polinomio tiene\(2 n\) grados de libertad, y\(n\) -punto Gauss cuadratura también da\(2 n\) grados de libertad (\(n\)puntos y\(n\) pesos).

Ejemplo 7.1.4 regla trapezoidal

La última regla de integración considerada es la regla trapezoidal, la cual se basa en el interpolante lineal formado mediante el uso de los puntos de interpolación\(\bar{x}^{1}=x_{i}\) y\(\bar{x}^{2}=x_{i+1}\) en cada segmento\(S_{i}=\left[x_{i}, x_{i+1}\right]\). La fórmula de integración viene dada por\[\begin{aligned} I_{h} &=\sum_{i=1}^{N-1} \int_{S_{i}}(\mathcal{I} f)(x) d x=\sum_{i=1}^{N-1} \int_{S_{i}}\left[f\left(x_{i}\right)+\left(\frac{f\left(x_{i+1}\right)-f\left(x_{i}\right)}{h}\right)\left(x-x_{i}\right)\right] \\ &=\sum_{i=1}^{N-1}\left[f\left(x_{i}\right) h+\frac{1}{2}\left(f\left(x_{i+1}\right)-f\left(x_{i}\right)\right) h\right] \\ &=\sum_{i=1}^{N-1} \frac{1}{2} h\left(f\left(x_{i}\right)+f\left(x_{i+1}\right)\right) . \end{aligned}\] Como los puntos de evaluación de la función global están relacionados con los puntos de segmentación por\(\tilde{x}_{i}=x_{i}, i=\)\(1, \ldots, N\), la regla de cuadratura también se puede expresar como\[I_{h}=\sum_{i=1}^{N-1} \frac{1}{2} h\left(f\left(\tilde{x}_{i}\right)+f\left(\tilde{x}_{i+1}\right)\right),\] Reordenando la ecuación, podemos escribir la regla de integración como \[I_{h}=\sum_{i=1}^{N-1} \frac{1}{2} h\left(f\left(\tilde{x}_{i}\right)+f\left(\tilde{x}_{i+1}\right)\right)=\frac{1}{2} h f\left(\tilde{x}_{1}\right)+\sum_{i=2}^{N-1}\left[h f\left(\tilde{x}_{i}\right)\right]+\frac{1}{2} h f\left(\tilde{x}_{N}\right) .\]Tenga en cuenta que esta regla de cuadratura asigna un peso de cuadratura diferente a los puntos de cuadratura en el límite del dominio desde los puntos en el interior del dominio. La regla de integración se ilustra en la Figura 7.5 (a).

Usando la fórmula general de integración, Ec. (7.7), obtenemos el límite de error\[\left|I-I_{h}\right| \leq(b-a) e_{\max }=(b-a) \frac{h^{2}}{8} \max _{x \in[a, b]}\left|f^{\prime \prime}(x)\right| .\]

(a) integral

(b) error

Figura 7.5: Regla trapezoidal.

Esta encuadernación puede ser apretada por un factor constante, cediendo\[\left|I-I_{h}\right| \leq(b-a) e_{\max }=(b-a) \frac{h^{2}}{12} \max _{x \in[a, b]}\left|f^{\prime \prime}(x)\right|\] que es agudo. El límite de error muestra que el esquema es exacto de segundo orden.

Prueba

Para probar el límite agudo del error de integración, recuerde el siguiente resultado intermedio de la prueba del error de interpolación lineal, Ec. (2.3),\[f(x)-(\mathcal{I} f)(x)=\frac{1}{2} f^{\prime \prime}\left(\xi_{i}\right)\left(x-x_{i}\right)\left(x-x_{i+1}\right)\] para algunos\(\xi_{i} \in\left[x_{i}, x_{i+1}\right]\). Integrando la expresión sobre el segmento\(S_{i}\), obtenemos la representación de error local\[\begin{aligned} I^{n}-I_{h}^{n} &=\int_{x_{i}}^{x_{i+1}} f(x)-(\mathcal{I} f)(x) d x=\int_{x_{i}}^{x_{i+1}} \frac{1}{2} f^{\prime \prime}\left(\xi_{i}\right)\left(x-x_{i}\right)\left(x-x_{i+1}\right) d x \\ & \leq \int_{x_{i}}^{x_{i+1}} \frac{1}{2}\left|f^{\prime \prime}\left(\xi_{i}\right)\left(x-x_{i}\right)\left(x-x_{i+1}\right)\right| d x \leq\left(\int_{x_{i}}^{x_{i+1}} \frac{1}{2}\left|\left(x-x_{i}\right)\left(x-x_{i+1}\right)\right| d x\right)_{\xi \in\left[x_{i}, x_{i+1}\right]}\left|f^{\prime \prime}(\xi)\right| \\ &=\frac{1}{12}\left(x_{i+1}-x_{i}\right)^{3} \max _{\xi \in\left[x_{i}, x_{i+1}\right]}\left|f^{\prime \prime}(\xi)\right|=\frac{1}{12} h^{3} \max _{\xi \in\left[x_{i}, x_{i+1}\right]}\left|f^{\prime \prime}(\xi)\right| \end{aligned}\] Sumando los errores locales, obtenemos el límite de error global\[\left|I-I_{h}\right|=\left|\sum_{i=1}^{N} \frac{1}{12} h^{3} \max _{\xi_{i} \in\left[x_{i}, x_{i+1}\right]}\right| f^{\prime \prime}\left(\xi_{i}\right)\left|\leq \frac{1}{12}(b-a) h^{2} \max _{x \in[a, b]}\right| f^{\prime \prime}(x) \mid\]

(a) integral

(b) error

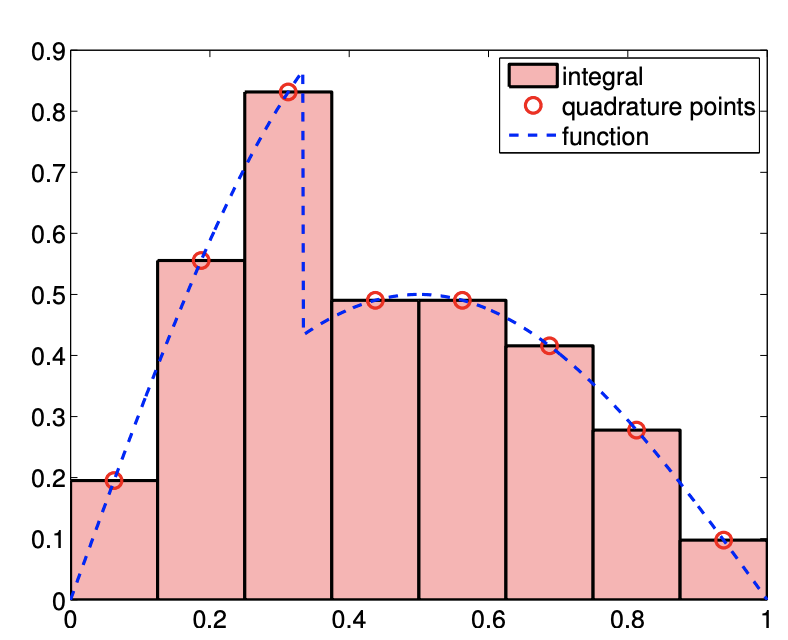
Figura 7.6: Integración de una función no suave.

Antes de concluir esta sección, hagamos algunas observaciones sobre la integración de una función no fluida. Para la interpolación, vimos que el error máximo no puede ser mejor que\(h^{r}\), donde\(r\) está la derivada de orden más alto que se define en todas partes del dominio. Para la integración, el requisito de regularidad es menos estricto. Para ver esto, volvamos a considerar nuestra función discontinua\[f(x)=\left\{\begin{array}{ll} \sin (\pi x), & x \leq \frac{1}{3} \\ \frac{1}{2} \sin (\pi x), & x>\frac{1}{3} \end{array} .\right.\] El resultado de aplicar la regla de integración de punto medio con ocho intervalos se muestra en la Figura 7.6 (a). Intuitivamente, podemos ver que el área cubierta por la aproximación se acerca a la del área verdadera incluso en presencia de la discontinuidad como\(h \rightarrow 0\). La cifra\(7.6(\mathrm{~b})\) confirma que efectivamente así es el caso. Todos los esquemas considerados convergen a razón de\(h^{1}\). La tasa de convergencia para el punto medio y las reglas trapezoidales se reducen a\(h^{1}\) de\(h^{2}\). Formalmente, podemos demostrar que los esquemas de integración convergen a la velocidad de\(\min (k, r+1)\), donde\(k\) está el orden de precisión del esquema de integración para un problema suave, y\(r\) es el derivado de orden más alto de\(f\) que se define en todas partes del dominio. En términos de precisión, la integración suaviza y así ayuda, mientras que la diferenciación amplifica las variaciones y, por lo tanto, duele.