7.2: Integración de Funciones Bivariadas

Al tener funciones bivariadas interpoladas, ahora consideramos la integración de funciones bivariadas. Deseamos aproximar\[I=\iint_{D} f(x, y) d x d y .\] Siguiendo el enfoque utilizado para integrar funciones univariadas, reemplazamos la función\(f\) por su interpolante e integramos exactamente el interpolante.

(a) integral

(b) error

Figura 7.7: Regla del punto medio.

Triangulamos el dominio\(D\) como se muestra en la Figura\(2.15\) para construir interpolantes. Entonces, aproximamos la integral como la suma de las contribuciones de los triángulos, es decir\(\left\{R_{i}\right\}_{i=1}^{N}\),\[I=\sum_{i=1}^{N} \iint_{R_{i}} f(x, y) d x d y \approx \sum_{i=1}^{N} \iint_{R_{i}}(\mathcal{I} f)(x, y) d x d y \equiv I_{h}\] Consideramos ahora dos ejemplos de reglas de integración.

Ejemplo 7.2.1 regla de punto medio

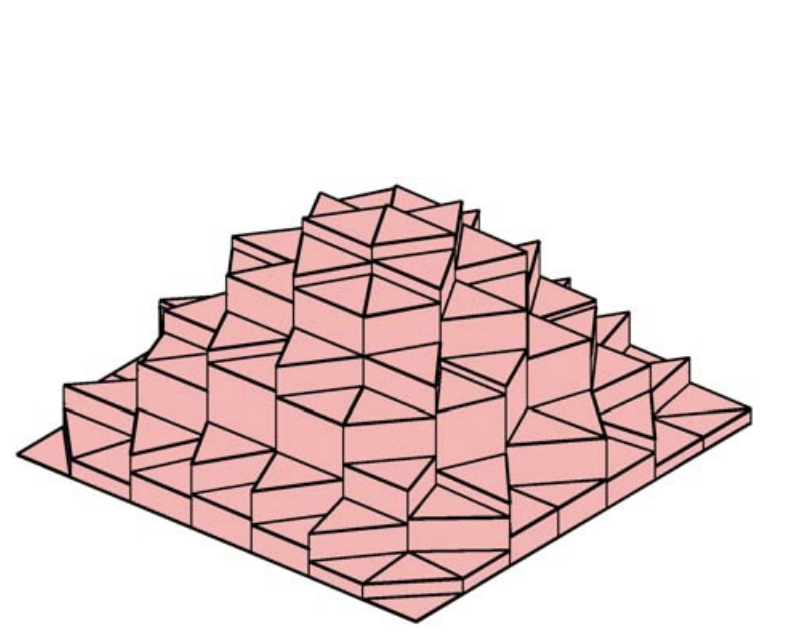
La primera regla es la regla de punto medio basada en el interpolante de punto medio constante por partes. Recordemos, el interpolante sobre\(R_{i}\) se define por el valor de la función en su centroide,\[(\mathcal{I} f)(\boldsymbol{x})=f\left(\tilde{\boldsymbol{x}}_{i}\right)=f\left(\boldsymbol{x}_{i}^{c}\right), \quad \forall \boldsymbol{x} \in R^{n}\] donde el centroide se da promediando las coordenadas del vértice,\[\tilde{\boldsymbol{x}}_{i}=\boldsymbol{x}_{i}^{c}=\frac{1}{3} \sum_{i=1}^{3} \boldsymbol{x}_{i}\] La integral se aproxima por\[I_{h}=\sum_{i=1}^{N} \iint_{R_{i}}(\mathcal{I} f)(x, y) d x d y=\sum_{i=1}^{N} \iint_{R_{i}} f\left(\tilde{x}_{i}, \tilde{y}_{i}\right) d x d y=\sum_{i=1}^{N} A_{i} f\left(\tilde{x}_{i}, \tilde{y}_{i}\right)\] donde hemos utilizado el hecho\[\iint_{R_{i}} d x d y=A_{i}\] con\(A_{i}\) denotar el área del triángulo\(R_{i}\). El proceso de integración se muestra pictóricamente en la Figura\(7.7(\mathrm{a})\). Tenga en cuenta que se trata de una generalización de la regla de punto medio a dos dimensiones.

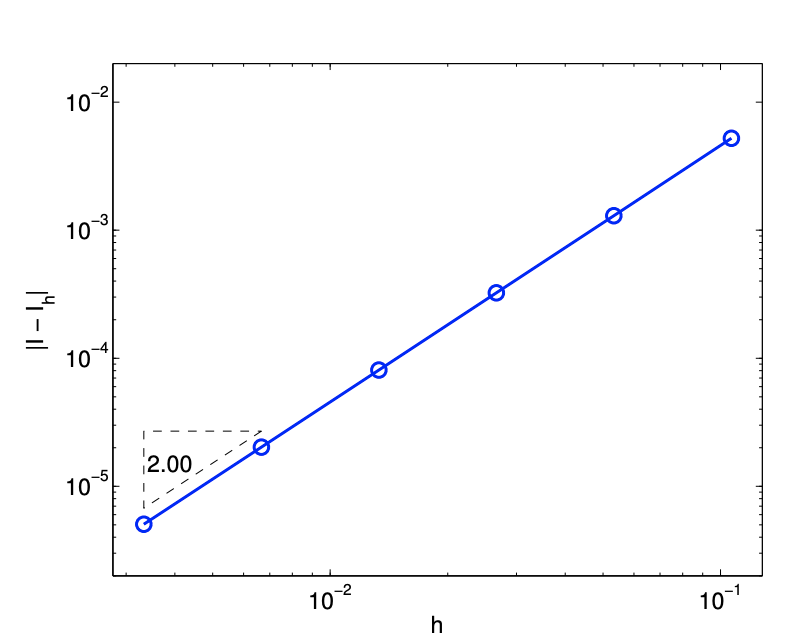
El error en la integración está limitado por\[e \leq C h^{2}\left\|\nabla^{2} f\right\|_{F}\]

(a) integral

(b) error

Figura 7.8: Regla trapezoidal.

Por lo tanto, la regla de integración es precisa de segundo orden. Se muestra un ejemplo de convergencia de error en la Figura 7.7 (b), donde los triángulos se dividen uniformemente para producir una mejor aproximación de la integral. La trama de convergencia confirma la convergencia de segundo orden del esquema.

Similar a la regla del punto medio en una dimensión, la regla del punto medio en un triángulo también pertenece a la familia de cuadraturas Gauss. Los puntos y pesos de cuadratura se eligen de manera óptima para lograr una convergencia de orden tan alto como sea posible.

Ejemplo 7.2.2 regla trapezoidal

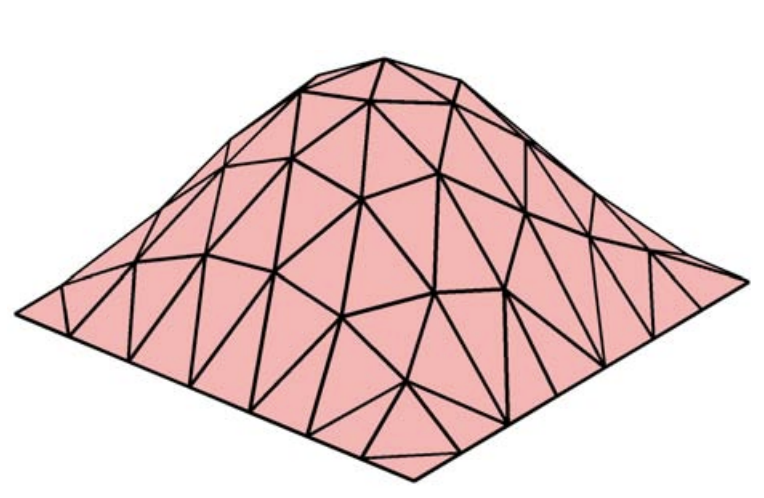
La regla de integración trapezoidal se basa en el interpolante lineal por tramos. Debido a que la integral de una función lineal definida en un parche triangular es igual al promedio de los valores de la función en sus vértices por el área del triángulo, la integral simplifica a\[I_{h}=\sum_{i=1}^{N}\left[\frac{1}{3} A_{i} \sum_{m=1}^{3} f\left(\bar{x}_{i}^{m}\right)\right]\] donde\(\left\{\overline{\boldsymbol{x}}_{i}^{1}, \overline{\boldsymbol{x}}_{i}^{2}, \overline{\boldsymbol{x}}_{i}^{3}\right\}\) están los vértices del triángulo\(R_{i}\). El proceso de integración se muestra gráficamente en la Figura 7.8 (a).

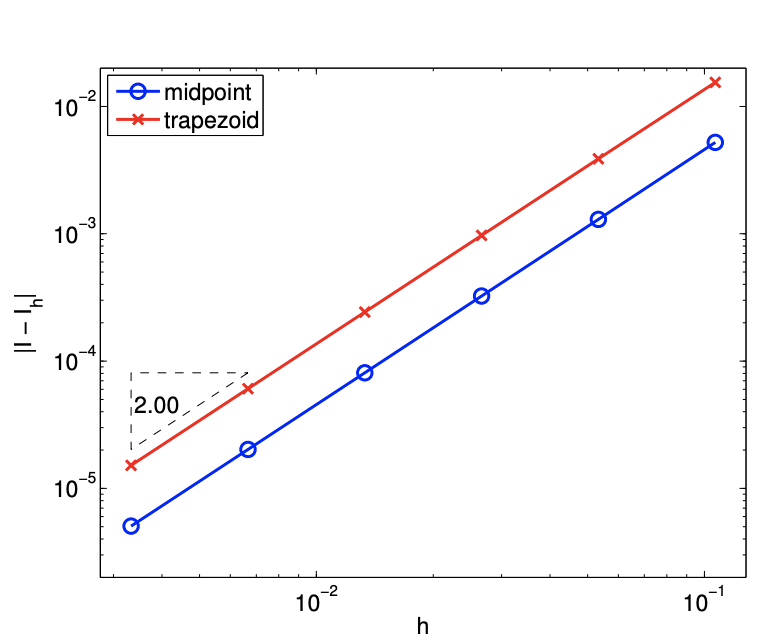
El error en la integración está limitado por\[e \leq C h^{2}\left\|\nabla^{2} f\right\|_{F}\] La regla de integración es precisa de segundo orden, como lo confirma la gráfica de convergencia que se muestra en la Figura\(7.8(\mathrm{~b})\).

Las reglas de integración se extienden a dimensiones superiores en principio mediante el uso de reglas de interpolación para dimensiones superiores. Sin embargo, el número de puntos de integración aumenta a medida que\((1 / h)^{d}\), dónde\(d\) está la dimensión física. El número de puntos aumenta exponencialmente en\(d\), y esto se llama la maldición de la dimensionalidad. Una alternativa es utilizar un proceso de integración basado en números aleatorios, el cual se discute en la siguiente unidad.