19.1: Caso más simple

Consideremos primero un caso “simple” de regresión, donde nos limitamos a una variable independiente y funciones de base lineal.

Problema de determinación del coeficiente de fricción revisitado

Recordemos el problema de determinación del coeficiente de fricción que consideramos en la Sección\(17.1\). Hemos visto que en presencia de mediciones\(m\) perfectas, podemos encontrar una\(\mu_{\mathrm{s}}\) que satisfaga\(m\) ecuaciones\[F_{\mathrm{f}, \text { static } i}^{\max }=\mu_{\mathrm{s}} F_{\text {normal, applied } i}, \quad i=1, \ldots, m\] En otras palabras, podemos usar cualquiera de las\(m\) -mediciones y resolver para\(\mu_{s}\) según \[\mu_{\mathrm{s}, i}=\frac{F_{\mathrm{f}, \text { static } i}^{\max , \text { meas }}}{F_{\text {normal, applied } i}}\]y todos\(\mu_{\mathrm{s}, i}, i=1, \ldots, m\), serán idénticos y estarán de acuerdo con el verdadero valor\(\mu_{\mathrm{s}}\).

Desafortunadamente, las mediciones reales están corruptas por el ruido. En particular, es poco probable que podamos encontrar un solo coeficiente que satisfaga todos los pares\(m\) de medición. En otras palabras,\(\mu_{\mathrm{s}}\) calculados usando los\(m\) diferentes pares es probable que no sean idénticos. Un modelo más adecuado para la fricción estática que incorpora la noción de ruido de medición es\[F_{\mathrm{f}, \text { static }}^{\max , \text { meas }}=\mu_{\mathrm{S}} F_{\text {normal, applied }}+\epsilon .\] El ruido asociado a cada medición es obviamente desconocido (de lo contrario podríamos corregir las mediciones), por lo que la ecuación en la forma actual no es muy útil. Sin embargo, si hacemos algunas suposiciones débiles sobre el comportamiento del ruido, de hecho podemos:

a) inferir el valor de la confianza\(\mu_{\mathrm{s}}\) asociada,

b) estimar el nivel de ruido,

(c) confirmar que nuestro modelo es correcto (más precisamente, no incorrecto),

d) y detectar efectos significativos no modelados. Esta es la idea detrás de la regresión — un marco para deducir la relación entre un conjunto de entradas (por ejemplo\(F_{\text {normal,applied }}\)) y las salidas (por ejemplo\(F_{\mathrm{f}, \text { static }}^{\text {max }}\)) en presencia de ruido. El marco de regresión consta de dos etapas:\((i)\) construcción de un modelo de respuesta apropiado y (ii) identificación de los parámetros del modelo a partir de datos. Ahora desarrollaremos procedimientos para llevar a cabo estas tareas.

Modelo de respuesta

Describamos la relación entre la entrada\(x\) y la salida\(Y\) por\[Y(x)=Y_{\text {model }}(x ; \beta)+\epsilon(x),\] donde

(a)\(x\) es la variable independiente, que es determinista.

(b)\(Y\) es la cantidad medida (es decir, datos), que en general es ruidosa. Debido a que se supone que el ruido es aleatorio,\(Y\) es una variable aleatoria.

(c)\(Y_{\text {model }}\) es el modelo predictivo sin ruido. En regresión lineal,\(Y_{\text {model }}\) es una función lineal del parámetro del modelo\(\beta\) por definición. Además, suponemos aquí que el modelo es una función afín de\(x\), es decir,\[Y_{\text {model }}(x ; \beta)=\beta_{0}+\beta_{1} x,\] dónde\(\beta_{0}\) y\(\beta_{1}\) son los componentes del parámetro del modelo\(\beta\). Relajaremos esta\(x\) suposición en la siguiente sección y consideraremos dependencias funcionales más generales, así como variables independientes adicionales.

\((d) \epsilon\)es el ruido, que es una variable aleatoria.

Nuestro objetivo es inferir el parámetro del modelo\(\beta\) que mejor describa el comportamiento de la cantidad medida y construir un modelo\(Y_{\text {model }}(\cdot ; \beta)\) que pueda usarse para predecir la salida para una nueva\(x\). (Tenga en cuenta que en algunos casos, la estimación del parámetro en sí puede ser de interés, por ejemplo, deduciendo el coeficiente de fricción. En otros casos, el interés principal puede ser predecir la salida usando el modelo, por ejemplo, predecir la fuerza de fricción para una fuerza normal dada. En el segundo caso, la estimación del parámetro en sí es simplemente un medio para el final.)

Como se considera en la Sección 17.1, asumimos que nuestro modelo es imparcial. Es decir, en ausencia de ruido\((\epsilon=0)\), nuestra relación subyacente entrada-salida puede ser perfectamente descrita por\[y(x)=Y_{\text {model }}\left(x ; \beta^{\text {true }}\right)\] para algún parámetro “verdadero”\(\beta^{\text {true }}\). En otras palabras, nuestro modelo incluye la verdadera dependencia funcional (pero puede incluir más generalidad de la que realmente se necesita). Observamos en Sección\(17.1\) que si el modelo es imparcial y las mediciones están libres de ruido, entonces podemos deducir el parámetro verdadero,\(\beta^{\text {true }}\), utilizando un número de puntos de datos igual o mayor que los grados de libertad del modelo\((m \geq n)\).

En este capítulo, si bien seguimos asumiendo que el modelo es imparcial\({ }_{-}^{1}\), relajamos la suposición libre de ruido. Nuestra medición (es decir, datos) es ahora de la forma\[Y(x)=Y_{\text {model }}\left(x ; \beta^{\text {true }}\right)+\epsilon(x),\] donde\(\epsilon\) está el ruido. Para estimar el parámetro verdadero\(\beta^{\text {true }}\), con confianza, hacemos tres suposiciones importantes sobre el comportamiento del ruido. Estos supuestos nos permiten hacer afirmaciones cuantitativas (estadísticas) sobre la calidad de nuestra regresión.

\({ }^{1}\)En la Sección 19.2.4, consideraremos los efectos del sesgo (o submodelización) en uno de los ejemplos.

Figura 19.1: Ilustración del proceso de regresión.

(\(i\)) Normalidad (N1): Suponemos que el ruido es un ruido normalmente distribuido con media cero, es decir,\(\epsilon(x) \sim\)\(\mathcal{N}\left(0, \sigma^{2}(x)\right)\). Así, el ruido\(\epsilon(x)\) es descrito por un solo parámetro\(\sigma^{2}(x)\).

(\(ii\)) Homocedasticidad (N2): Asumimos que no\(\epsilon\) es una función de\(x\) en el sentido de que la distribución de\(\epsilon\), en particular\(\sigma^{2}\), no dependa de\(x\).

(\(iii\)) Independencia (N3): Suponemos que\(\epsilon\left(x_{1}\right)\) y\(\epsilon\left(x_{2}\right)\) son independientes y por lo tanto no correlacionados.

Nos referiremos a estos tres supuestos como (N1), (N2) y (N3) a lo largo del resto del capítulo. Estos supuestos implican que\(\epsilon(x)=\epsilon=\mathcal{N}\left(0, \sigma^{2}\right)\), ¿dónde\(\sigma^{2}\) está el parámetro único para todas las instancias de\(x\).

Obsérvese que porque\[Y(x)=Y_{\text {model }}(x ; \beta)+\epsilon=\beta_{0}+\beta_{1} x+\epsilon\] y\(\epsilon \sim \mathcal{N}\left(0, \sigma^{2}\right)\), el modelo determinista\(Y_{\text {model }}(x ; \beta)\) simplemente desplaza la media de la distribución normal. Así, la medición es una variable aleatoria con la distribución\[Y(x) \sim \mathcal{N}\left(Y_{\text {model }}(x ; \beta), \sigma^{2}\right)=\mathcal{N}\left(\beta_{0}+\beta_{1} x, \sigma^{2}\right) .\] En otras palabras, cuando realizamos una medición en algún momento\(x_{i}\), estamos en teoría dibujando una variable aleatoria a partir de la distribución\(\mathcal{N}\left(\beta_{0}+\beta_{1} x_{i}, \sigma^{2}\right)\). Podemos pensar en una variable aleatoria (con media) parametrizada por\(x\), o podemos pensar en\(Y(x)\) como una función aleatoria (a menudo denotada como un proceso aleatorio).\(Y(x)\)

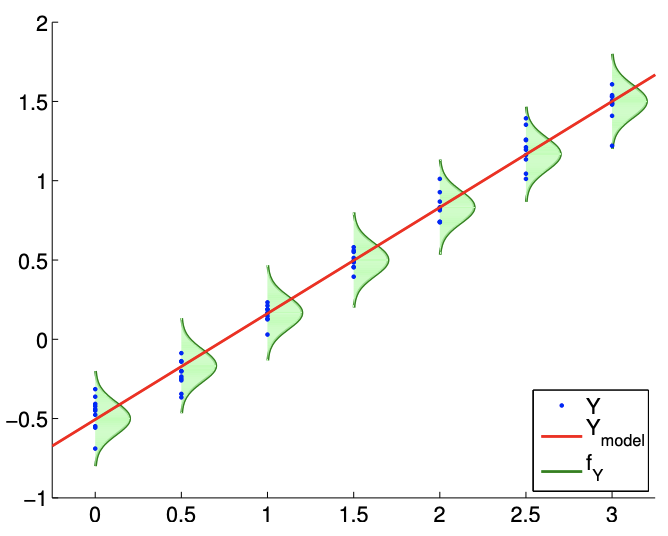
Un proceso de regresión típico se ilustra en la Figura 19.1. El modelo\(Y_{\text {model }}\) es una función lineal de la forma\(\beta_{0}+\beta_{1} x\). Las funciones de densidad de probabilidad de\(Y, f_{Y}\), muestran que el error se distribuye normalmente (N1) y que la varianza no cambia con\(x\) (N2). Las realizaciones de\(Y\) muestreadas para\(x=0.0,0.5,1.0, \ldots, 3.0\) confirman que es poco probable que las realizaciones caigan fuera de los\(3 \sigma\) límites trazados. (Recordemos que\(99.7 \%\) de las muestras cae dentro de\(3 \sigma\) los límites para una distribución normal.)

La figura\(19.1\) sugiere que el resultado probable de\(Y\) depende de nuestra variable\(x\) independiente de manera lineal. Esto no quiere decir que\(Y\) sea una función de\(x\) sólo. En particular, el resultado de un experimento es en general una función de muchas variables independientes,\[x=\left(\begin{array}{llll} x_{(1)} & x_{(2)} & \cdots & x_{(k)} \end{array}\right)\] Pero, al construir nuestro modelo, asumimos que el resultado solo depende fuertemente del comportamiento de\(x=x_{(1)}\), y el efecto neto de las otras variables\(\left(\begin{array}{ccc}x_{(2)} & \cdots & x_{(k)}\end{array}\right)\) puede ser modelado como aleatorio a través de\(\epsilon\). En otras palabras, el proceso subyacente que gobierna la relación input-output puede ser completamente determinista si se nos dan\(k\) variables que proporcionan la descripción completa del sistema, es decir,\[y\left(x_{(1)}, x_{(2)}, \ldots, x_{(k)}\right)=f\left(x_{(1)}, x_{(2)}, \ldots, x_{(k)}\right) .\] sin embargo, es poco probable que tengamos el conocimiento completo de las funciones dependencias así como el estado del sistema.

Sabiendo que la predicción determinista de la salida es intratable, recurrimos a comprender la dependencia funcional de la variable más significativa, digamos\(x_{(1)}\). Si sabemos que la dependencia de\(y\) on\(x_{(1)}\) es más dominante afín (digamos, basado en una ley física), entonces podemos dividir nuestra dependencia funcional (intratable) en\[y\left(x_{(1)}, x_{(2)}, \ldots, x_{(k)}\right)=\beta_{0}+\beta_{1} x_{(1)}+g\left(x_{(1)}, x_{(2)}, \ldots, x_{(k)}\right) .\] Aquí\(g\left(x_{(1)}, x_{(2)}, \ldots, x_{(k)}\right)\) incluye tanto el comportamiento del sistema sin modelar como el no modelado proceso que conduce a errores de medición. En este punto, asumimos que el efecto de\(\left(x_{(2)}, \ldots, x_{(k)}\right)\) on\(y\) y el efecto débil de\(x_{(1)}\) on\(y\) through\(g\) pueden agruparse en una variable aleatoria de media cero\(\epsilon\), es decir,\[Y\left(x_{(1)} ; \beta\right)=\beta_{0}+\beta_{1} x_{(1)}+\epsilon .\] En algún nivel esta ecuación está casi garantizada para estar equivocada.

Primero, habrá algún sesgo: aquí sesgo se refiere a una desviación de la media de\(Y(x)\) desde\(\beta_{0}+\beta_{1} x_{(1)}\) - que por supuesto no puede ser representada por la\(\epsilon\) cual se supone media cero. En segundo lugar, nuestro modelo para el ruido (por ejemplo, (N1), (N2), (N3)) -de hecho, cualquier modelo para el ruido- ciertamente no es perfecto. Sin embargo, si el sesgo es pequeño y las desviaciones del ruido de nuestros supuestos (N1), (N2) y (N3) son pequeñas, nuestros procedimientos suelen proporcionar buenas respuestas. De ahí que siempre debemos cuestionarnos si el modelo de respuesta\(Y_{\text {model }}\) es correcto, en el sentido de que incluye el modelo correcto. Además, los supuestos (N1), (N2) y (N3) no se aplican a todos los procesos físicos y deben tratarse con escepticismo.

También observamos que el número apropiado de variables independientes que se modelan explícitamente, sin ser agrupadas en la variable aleatoria, depende del sistema. (En la siguiente sección, trataremos el caso en el que debemos considerar las dependencias funcionales en más de una variable independiente). Solidifiquemos la idea usando un ejemplo muy sencillo de múltiples volteos de monedas en los que de hecho no necesitamos considerar ninguna variable independiente.

Ejemplo 19.1.1 Dependencias funcionales en volteretas de monedas

Digamos que el sistema es de 100 tiradas de monedas justas y\(Y\) es el número total de cabezas. El resultado de cada volteo de moneda, que afecta a la salida\(Y\), es una función de muchas variables: la masa de la moneda, el momento de inercia de la moneda, la velocidad de lanzamiento inicial, el momento angular inicial, la elasticidad de la superficie, la densidad del aire, etc. si tuviéramos una descripción completa del ambiente, entonces el resultado de cada volteo de moneda es determinista, gobernado por las ecuaciones de Euler (para la dinámica del cuerpo rígido), las ecuaciones de Navier-Stokes (para la dinámica del aire), etc. Vemos que este enfoque determinista hace que nuestra simulación sea intratable, tanto en términos del número de estados como del funcional dependencias incluso para algo tan simple como voltear monedas.

Así, tomamos un enfoque alternativo y agrupamos algunas de las dependencias funcionales en una variable aleatoria. Del Capítulo 9, sabemos que\(Y\) tendrá una distribución binomial\(\mathcal{B}(n=100, \theta=\)\(1 / 2)\). La media y la varianza de\(Y\) son\[E[Y]=n \theta=50 \text { and } E\left[\left(Y-\mu_{Y}\right)^{2}\right]=n \theta(1-\theta)=25 .\] De hecho, por el teorema del límite central, sabemos que se\(Y\) puede aproximar por\[Y \sim \mathcal{N}(50,25) .\] El hecho de que se\(Y\) puede modelar como\(\mathcal{N}(50,25)\) sin ninguna dependencia explícita de ninguna de las muchas variables independientes que citamos anteriormente no significa que\(Y\) no dependa de las variables. Solo significa que el efecto acumulativo de todas las variables independientes en se\(Y\) puede modelar como una variable aleatoria normal de media cero. Esto quizás pueda estar motivado de manera más general por el teorema del límite central, que heurísticamente justifica el tratamiento de muchos pequeños efectos aleatorios como ruido normal.

Estimación de parámetros

Ahora realizamos\(m\) experimentos, cada uno de los cuales se caracteriza por la variable independiente\(x_{i}\). Cada experimento descrito por\(x_{i}\) resultados en una medición\(Y_{i}\), y recogemos pares de\(m\) medición-variable,\[\left(x_{i}, Y_{i}\right), \quad i=1, \ldots, m .\] en general, el valor de las variables independientes\(x_{i}\) puede repetirse. Suponemos que nuestras mediciones satisfacen\[Y_{i}=Y_{\text {model }}\left(x_{i} ; \beta\right)+\epsilon_{i}=\beta_{0}+\beta_{1} x_{i}+\epsilon_{i} .\] A partir de los experimentos, deseamos estimar el parámetro verdadero\(\beta^{\text {true }}=\left(\beta_{0}^{\text {true }}, \beta_{1}^{\text {true }}\right)\) sin el conocimiento preciso de\(\epsilon\) (que es descrito por\(\sigma\)). De hecho vamos a estimar\(\beta^{\text {true }}\) y\(\sigma\) por\(\hat{\beta}\) y\(\hat{\sigma}\), respectivamente.

Resulta, de nuestros supuestos (N1), (N2) y (N3), que el estimador de máxima verosimilitud (MLE) para\(\beta\) -el valor más probable para el parámetro dadas las mediciones\(\left(x_{i}, Y_{i}\right), i=1, \ldots, m\) - es precisamente nuestro ajuste de mínimos cuadrados, es decir,\(\hat{\beta}=\beta^{*}\). Es decir, si formamos\[X=\left(\begin{array}{cc} 1 & x_{1} \\ 1 & x_{2} \\ \vdots & \vdots \\ 1 & x_{m} \end{array}\right) \quad \text { and } \quad Y=\left(\begin{array}{c} Y_{1} \\ Y_{2} \\ \vdots \\ Y_{m} \end{array}\right)\] entonces el MLE,\(\hat{\beta}\), satisface\[\|X \hat{\beta}-Y\|_{2}<\|X \beta-Y\|_{2}, \quad \forall \beta \neq \hat{\beta} .\] Equivalentemente,\(\hat{\beta}\) satisface la ecuación normal\[\left(X^{\mathrm{T}} X\right) \hat{\beta}=X^{\mathrm{T}} Y .\] Proporcionamos la prueba.

Prueba

Mostramos que la solución de mínimos cuadrados es el estimador de máxima verosimilitud (MLE) para\(\beta\). Recordemos que consideramos cada medición como\(Y_{i}=\mathcal{N}\left(\beta_{0}+\beta_{1} x_{i}, \sigma^{2}\right)=\mathcal{N}\left(X_{i} \cdot \beta, \sigma^{2}\right)\). Al señalar que el ruido es independiente, la\(m\) medición define colectivamente una distribución conjunta,\[Y=\mathcal{N}(X \beta, \Sigma),\] donde\(\Sigma\) está la matriz de covarianza diagonal\(\Sigma=\operatorname{diag}\left(\sigma^{2}, \ldots, \sigma^{2}\right)\). Para encontrar el MLE, primero formamos la densidad de probabilidad condicional de\(Y\) asumir que\(\beta\) se da, es decir,\[f_{Y \mid \mathcal{B}}(y \mid \beta)=\frac{1}{(2 \pi)^{m / 1}|\Sigma|^{1 / 2}} \exp \left(-\frac{1}{2}(y-X \beta)^{\mathrm{T}} \Sigma^{-1}(y-X \beta)\right),\] que se puede ver como una función de verosimilitud si ahora arreglamos\(y\) y dejamos\(\beta\) variar\(-\beta \mid y\) en lugar de\(y \mid \beta\). El MLE -el\(\beta\) que maximiza la probabilidad de mediciones\(\left\{y_{i}\right\}_{i=1}^{m}\) - es entonces\[\hat{\beta}=\arg \max _{\beta \in \mathbb{R}^{2}} f_{Y \mid \mathcal{B}}(y \mid \beta)=\arg \max _{\beta \in \mathbb{R}^{2}} \frac{1}{(2 \pi)^{m / 1}|\Sigma|^{1 / 2}} \exp (-\underbrace{\frac{1}{2}(y-X \beta)^{\mathrm{T}} \Sigma^{-1}(y-X \beta)}_{J}) .\] El máximo se obtiene cuando\(J\) se minimiza. Así,\[\hat{\beta}=\arg \min _{\beta \in \mathbb{R}^{2}} J(\beta)=\arg \min _{\beta \in \mathbb{R}^{2}} \frac{1}{2}(y-X \beta)^{\mathrm{T}} \Sigma^{-1}(y-X \beta) .\] Recordando la forma de\(\Sigma\), podemos simplificar la expresión a\[\begin{aligned} \hat{\beta} &=\arg \min _{\beta \in \mathbb{R}^{2}} \frac{1}{2 \sigma^{2}}(y-X \beta)^{\mathrm{T}}(y-X \beta)=\arg \min _{\beta \in \mathbb{R}^{2}}(y-X \beta)^{\mathrm{T}}(y-X \beta) \\ &=\arg \min _{\beta \in \mathbb{R}^{2}}\|y-X \beta\|^{2} . \end{aligned}\] Este es precisamente el problema de mínimos cuadrados. Así, la solución al problema de mínimos cuadrados\(X \beta=y\) es el MLE.

Habiendo estimado el parámetro desconocido\(\beta^{\text {true }}\) por\(\hat{\beta}\), calculemos ahora el ruido\(\epsilon\) caracterizado por lo desconocido\(\sigma\) (que podemos pensar como\(\sigma^{\text {true }}\)). Nuestro estimador para\(\sigma, \hat{\sigma}\), es\[\hat{\sigma}=\left(\frac{1}{m-2}\|Y-X \hat{\beta}\|^{2}\right)^{1 / 2} .\] Note que\(\|Y-X \hat{\beta}\|\) es solo la raíz cuadrática media del residual como motivado por el enfoque de mínimos cuadrados antes. El factor de normalización\(1 /(m-2)\),, proviene del hecho de que hay puntos de\(m\) medición y dos parámetros para ajustarse. Si\(m=2\), entonces todos los datos van a ajustar los parámetros\(\left\{\beta_{0}, \beta_{1}\right\}\) -dos puntos determinan una línea- y no queda ninguno para estimar el error; así, en este caso, no podemos estimar el error. Tenga en cuenta que\[(X \hat{\beta})_{i}=\left.Y_{\text {model }}\left(x_{i} ; \beta\right)\right|_{\beta=\hat{\beta}} \equiv \widehat{Y}_{i}\] es nuestro modelo de respuesta evaluado en el parámetro\(\beta=\hat{\beta}\); así podemos escribir\[\hat{\sigma}=\left(\frac{1}{m-2}\|Y-\widehat{Y}\|^{2}\right)^{1 / 2} .\] En algún sentido,\(\hat{\beta}\) minimiza el inajuste y lo que queda se atribuye al ruido\(\hat{\sigma}\) (según nuestro modelo). Tenga en cuenta que utilizamos los datos en todos los puntos\(x_{1}, \ldots, x_{m}\),, para obtener una estimación de nuestro único parámetro,\(\sigma\); esto se debe a nuestra suposición de homocedasticidad (N2), que asume que\(\epsilon\) (y por lo tanto\(\sigma\)) es independiente de \(x\).

También observamos que la estimación de mínimos cuadrados conserva la media de las mediciones en el sentido de que\[\bar{Y} \equiv \frac{1}{m} \sum_{i=1}^{m} Y_{i}=\frac{1}{m} \sum_{i=1}^{m} \widehat{Y}_{i} \equiv \overline{\widehat{Y}}\]

Prueba

La preservación de la media es una consecuencia directa de que el estimador\(\hat{\beta}\) satisface la ecuación normal. Recordemos,\(\hat{\beta}\) satisface\[X^{\mathrm{T}} X \hat{\beta}=X^{\mathrm{T}} Y .\] Porque\(\widehat{Y}=X \hat{\beta}\), podemos escribir esto como\[X^{\mathrm{T}} \widehat{Y}=X^{\mathrm{T}} Y\] Recordando la interpretación “fila” del producto matriz-vector y señalando que la columna de\(X\) es todas unas, el primer componente del lado izquierdo es\[\left(X^{\mathrm{T}} \widehat{Y}\right)_{1}=\left(\begin{array}{lll} 1 & \cdots & 1 \end{array}\right)\left(\begin{array}{c} \widehat{Y}_{1} \\ \vdots \\ \widehat{Y}_{m} \end{array}\right)=\sum_{i=1}^{m} \widehat{Y}_{i}\] De igual manera, el primer componente del lado derecho es\[\left(X^{\mathrm{T}} Y\right)_{1}=\left(\begin{array}{lll} 1 & \cdots & 1 \end{array}\right)\left(\begin{array}{c} Y_{1} \\ \vdots \\ Y_{m} \end{array}\right)=\sum_{i=1}^{m} Y_{i}\] Así, tenemos lo\[\left(X^{\mathrm{T}} \widehat{Y}\right)_{1}=\left(X^{\mathrm{T}} Y\right)_{1} \quad \Rightarrow \quad \sum_{i=1}^{m} \widehat{Y}_{i}=\sum_{i=1}^{m} Y_{i},\] que demuestra que el modelo conserva la media.

Intervalos de confianza

Consideramos dos conjuntos de intervalos de confianza. El primer conjunto de intervalos de confianza, a los que nos referimos como intervalos de confianza individuales, son los intervalos asociados a cada parámetro individual. El segundo conjunto de intervalos de confianza, a los que nos referimos como intervalos de confianza conjuntos, son los intervalos asociados con el comportamiento conjunto de los parámetros.

Intervalos de confianza individuales

Introduzcamos una estimación para la covarianza de\(\hat{\beta}\),\[\widehat{\Sigma} \equiv \hat{\sigma}^{2}\left(X^{\mathrm{T}} X\right)^{-1} .\] Para nuestro caso con dos parámetros, la matriz de covarianza es\(2 \times 2\). A partir de nuestra estimación de la covarianza, podemos construir el intervalo de confianza para\(\beta_{0}\) as\[I_{0} \equiv\left[\hat{\beta}_{0}-t_{\gamma, m-2} \sqrt{\widehat{\Sigma}_{11}}, \hat{\beta}_{0}+t_{\gamma, m-2} \sqrt{\widehat{\Sigma}_{11}}\right],\] y el intervalo de confianza para\(\beta_{1}\) as\[I_{1} \equiv\left[\hat{\beta}_{1}-t_{\gamma, m-2} \sqrt{\widehat{\Sigma}_{22}}, \hat{\beta}_{1}+t_{\gamma, m-2} \sqrt{\widehat{\Sigma}_{22}}\right] .\] El coeficiente\(t_{\gamma, m-2}\) depende del nivel de confianza,\(\gamma\), y los grados de libertad,\(m-2\). Tenga en cuenta que la Longitud Media de los intervalos de confianza para\(\beta_{0}\) y\(\beta_{1}\) son iguales a\(t_{\gamma, m-2} \sqrt{\widehat{\Sigma}_{11}}\) y\(t_{\gamma, m-2} \sqrt{\widehat{\Sigma}_{22}}\), respectivamente.

El intervalo de confianza\(I_{0}\) es un intervalo tal que la probabilidad de que el parámetro\(\beta_{0}^{\text {true }}\) tome un valor dentro del intervalo es igual al nivel de confianza\(\gamma\), es decir,\[P\left(\beta_{0}^{\text {true }} \in I_{0}\right)=\gamma .\] Por separado, el intervalo de confianza\(I_{1}\) satisface \[P\left(\beta_{1}^{\text {true }} \in I_{1}\right)=\gamma .\]El parámetro\(t_{\gamma, q}\) es el valor que satisface\[\int_{-t_{\gamma, q}}^{t_{\gamma, q}} f_{T, q}(s) d s=\gamma,\] donde\(f_{T, q}\) está la función de densidad de probabilidad para la\(t\) distribución de Student con\(q\) grados de libertad. Recordamos la interpretación frecuentística de los intervalos de confianza de nuestra discusión anterior de la Unidad II.

Tenga en cuenta que podemos\(t_{\gamma, q}\) relacionarnos con la función de distribución acumulativa de la\(t\) -distribución,\(F_{T, q}\), de la siguiente manera. Primero, observamos que\(f_{T, q}\) es simétrico alrededor de cero. Así, tenemos\[\int_{0}^{t_{\gamma, q}} f_{T, q}(s) d s=\frac{\gamma}{2}\] y\[F_{T, q}(x) \equiv \int_{-\infty}^{x} f_{T, q}(s) d s=\frac{1}{2}+\int_{0}^{x} f_{T, q}(s) d s .\] Evaluando la función de distribución acumulativa en\(t_{\gamma, q}\) y sustituyendo la relación integral deseada,\[F_{T, q}\left(t_{\gamma, q}\right)=\frac{1}{2}+\int_{0}^{t_{\gamma, q}} f_{T, q}\left(t_{\gamma, q}\right) d s=\frac{1}{2}+\frac{\gamma}{2} .\] En particular, dada una función de distribución acumulativa inversa para la\(t\) distribución del Estudiante, podemos computar fácilmente\(t_{\gamma, q}\) como\[t_{\gamma, q}=F_{T, q}^{-1}\left(\frac{1}{2}+\frac{\gamma}{2}\right) .\] Por conveniencia, hemos tabulado los coeficientes para el nivel de\(95 \%\) confianza para seleccionar valores de grados de libertad en la Tabla 19.1 (a).

\(q\)	\(t_{\gamma, q} \mid \gamma=0.95\)
10	\(2.228\)
15	\(2.131\)
20	\(2.086\)
25	\(2.060\)
30	\(2.042\)
40	\(2.021\)
5	\(2.571\)
50	\(2.009\)
60	\(2.000\)
\(\infty\)	\(1.960\)

(a)\(t\) -distribución

\(q\)	\(k=1\)	2	3	4	5	10	15	20
5	\(2.571\)	\(3.402\)	\(4.028\)	\(4.557\)	\(5.025\)	\(6.881\)	\(8.324\)	\(9.548\)
10	\(2.228\)	\(2.865\)	\(3.335\)	\(3.730\)	\(4.078\)	\(5.457\)	\(6.533\)	\(7.449\)
15	\(2.131\)	\(2.714\)	\(3.140\)	\(3.496\)	\(3.809\)	\(5.044\)	\(6.004\)	\(6.823\)
20	\(2.086\)	\(2.643\)	\(3.049\)	\(3.386\)	\(3.682\)	\(4.845\)	\(5.749\)	\(6.518\)
25	\(2.060\)	\(2.602\)	\(2.996\)	\(3.322\)	\(3.608\)	\(4.729\)	\(5.598\)	\(6.336\)
30	\(2.042\)	\(2.575\)	\(2.961\)	\(3.280\)	\(3.559\)	\(4.653\)	\(5.497\)	\(6.216\)
40	\(2.021\)	\(2.542\)	\(2.918\)	\(3.229\)	\(3.500\)	\(4.558\)	\(5.373\)	\(6.064\)
50	\(2.009\)	\(2.523\)	\(2.893\)	\(3.198\)	\(3.464\)	\(4.501\)	\(5.298\)	\(5.973\)
60	\(2.000\)	\(2.510\)	\(2.876\)	\(3.178\)	\(3.441\)	\(4.464\)	\(5.248\)	\(5.913\)
\(\infty\)	\(1.960\)	\(2.448\)	\(2.796\)	\(3.080\)	\(3.327\)	\(4.279\)	\(5.000\)	\(5.605\)

(b)\(F\) -distribución

Cuadro 19.1: El coeficiente para computar el intervalo de\(95 \%\) confianza a partir de la\(t\) distribución y distribución\(F\) de Student.

Intervalos de confianza conjunta

A veces estamos más interesados en construir intervalos de confianza conjuntos, intervalos de confianza dentro de los cuales los valores verdaderos de todos los parámetros se encuentran en una fracción\(\gamma\) de todas las realizaciones. Estos intervalos de confianza se construyen esencialmente de la misma manera que los intervalos de confianza individuales y toman una forma similar. Intervalos de confianza conjunta para\(\beta_{0}\) y\(\beta_{1}\) son de la forma\[I_{0}^{\text {joint }} \equiv\left[\hat{\beta}_{0}-s_{\gamma, 2, m-2} \sqrt{\widehat{\Sigma}_{11}}, \hat{\beta}_{0}+s_{\gamma, 2, m-2} \sqrt{\widehat{\Sigma}_{11}}\right]\] y\[I_{1}^{\text {joint }} \equiv\left[\hat{\beta}_{1}-s_{\gamma, 2, m-2} \sqrt{\widehat{\Sigma}_{22}}, \hat{\beta}_{1}+s_{\gamma, 2, m-2} \sqrt{\widehat{\Sigma}_{22}}\right]\] Tenga en cuenta que el parámetro\(t_{\gamma, m-2}\) ha sido reemplazado por un parámetro\(s_{\gamma, 2, m-2}\). De manera más general, el parámetro toma la forma\(s_{\gamma, n, m-n}\), donde\(\gamma\) está el nivel de confianza,\(n\) es el número de parámetros en el modelo (aquí\(n=2\)), y\(m\) es el número de mediciones. Con el intervalo de confianza conjunta, tenemos\[P\left(\beta_{0}^{\text {true }} \in I_{0}^{\text {joint }} \text { and } \beta_{1}^{\text {true }} \in I_{1}^{\text {joint }}\right) \geq \gamma\] Nota la desigualdad -\(\geq \gamma-\) es porque nuestros intervalos son un “cuadro delimitador” para la elipse de confianza aguda real.

El parámetro\(s_{\gamma, k, q}\) está relacionado con\(\gamma\) -cuantil para la\(F\) -distribución,\(g_{\gamma, k, q}\), por\[s_{\gamma, k, q}=\sqrt{k g_{\gamma, k, q}}\] Note\(g_{\gamma, k, q}\) satisface\[\int_{0}^{g_{\gamma, k, q}} f_{F, k, q}(s) d s=\gamma\] donde\(f_{F, k, q}\) está la función de densidad de probabilidad del \(F\)-distribución; también podemos expresar\(g_{\gamma, k, q}\) en términos de la función de distribución acumulativa de la\(F\) -distribución como\[F_{F, k, q}\left(g_{\gamma, k, q}\right)=\int_{0}^{g_{\gamma, k, q}} f_{F, k, q}(s) d s=\gamma\] En particular, podemos escribir explícitamente\(s_{\gamma, k, q}\) usando la distribución acumulativa inversa para el \(F\)distribución, es decir\[s_{\gamma, k, q}=\sqrt{k g_{\gamma, k, q}}=\sqrt{k F_{F, k, q}^{-1}(\gamma)} .\] Por conveniencia, hemos tabulado los valores de\(s_{\gamma, k, q}\) para varias combinaciones diferentes de\(k\) y\(q\) en la Tabla 19.1 (b).

Observamos que\[s_{\gamma, k, q}=t_{\gamma, q}, \quad k=1,\] como se esperaba, porque la distribución conjunta es la misma que la distribución individual para el caso con un parámetro. Además,\[s_{\gamma, k, q}>t_{\gamma, q}, \quad k>1,\] indicando que los intervalos de confianza conjunta son mayores que los intervalos de confianza individuales. En otras palabras, los intervalos de confianza individuales son demasiado pequeños para producir conjuntamente lo deseado\(\gamma\).

Podemos entender estos intervalos de confianza con algunos ejemplos simples.

Ejemplo 19.1.2 Estimación de mínimos cuadrados para un modelo constante

Consideremos un modelo de respuesta simple de la forma\[Y_{\text {model }}(x ; \beta)=\beta_{0},\] donde\(\beta_{0}\) está el parámetro único a determinar. El sistema sobredeterminado viene dado por\[\left(\begin{array}{c} Y_{1} \\ Y_{2} \\ \vdots \\ Y_{m} \end{array}\right)=\left(\begin{array}{c} 1 \\ 1 \\ \vdots \\ 1 \end{array}\right) \beta_{0}=X \beta_{0}\] y reconocemos\(X=\left(\begin{array}{llll}1 & 1 & \cdots & 1\end{array}\right)^{\mathrm{T}}\). Tenga en cuenta que tenemos\[X^{\mathrm{T}} X=m\] Para este sistema simple, podemos desarrollar una expresión explícita para la estimación de mínimos cuadrados para\(\beta_{0}^{\text {true }}, \hat{\beta}_{0}\) resolviendo la ecuación normal, es decir,\[X^{\mathrm{T}} X \hat{\beta}_{0}=X^{\mathrm{T}} Y \quad \Rightarrow \quad m \hat{\beta}_{0}=\sum_{i=1}^{m} Y_{i} \quad \Rightarrow \quad \hat{\beta}_{0}=\frac{1}{m} \sum_{i=1}^{m} Y_{i}\] Nuestro estimador de parámetros\(\hat{\beta}_{0}\) es (no sorprendentemente) idéntico a la media muestral de Capítulo 11 ya que nuestro modelo aquí\(Y=\mathcal{N}\left(\beta_{0}^{\text {true }}, \sigma^{2}\right)\) es idéntico al modelo del Capítulo 11.

La matriz de covarianza (que es un escalar para este caso),\[\widehat{\Sigma}=\hat{\sigma}^{2}\left(X^{\mathrm{T}} X\right)^{-1}=\hat{\sigma}^{2} / m .\] Así, el intervalo de confianza,\(I_{0}\), tiene el Half Length\[\text { Half Length }\left(I_{0}\right)=t_{\gamma, m-1} \sqrt{\widehat{\Sigma}}=t_{\gamma, m-1} \hat{\sigma} / \sqrt{m} \text {. }\]

(a)\(m=14\)

b)\(m=140\)

Figura 19.2: Ajuste de mínimos cuadrados de una función constante utilizando un modelo constante.

Nuestra confianza en el estimador\(\hat{\beta}_{0}\) converge como\(1 / \sqrt{m}=m^{-1 / 2}\). Nuevamente, la tasa de convergencia es idéntica a la del Capítulo\(11 .\)

Como ejemplo, considere una función aleatoria de la forma\[Y \sim \frac{1}{2}+\mathcal{N}\left(0, \sigma^{2}\right),\] con la varianza\(\sigma^{2}=0.01\), y un modelo de respuesta constante (polinomio), es decir,\[Y_{\operatorname{model}}(x ; \beta)=\beta_{0}\] Tenga en cuenta que el parámetro true viene dado por\(\beta_{0}^{\text {true }}=1 / 2\). Nuestro objetivo es calcular la estimación de mínimos cuadrados de\(\beta_{0}^{\text {true }}, \hat{\beta}_{0}\), y la estimación del intervalo de confianza asociada,\(I_{0}\). Tomamos medidas en siete puntos,\(x=0,0.5,1.0, \ldots, 3.0 ;\) en cada punto tomamos\(n_{\text {sample}}\) medidas para el total de\(m = 7 \cdot n_{\text{sample}}\) mediciones. Varias mediciones (o replicación) a la vez\(x\) pueden ser ventajosas, como veremos en breve; sin embargo también es posible en particular gracias a nuestra suposición homoscedástica tomar solo una sola medición a cada valor de\(x\).

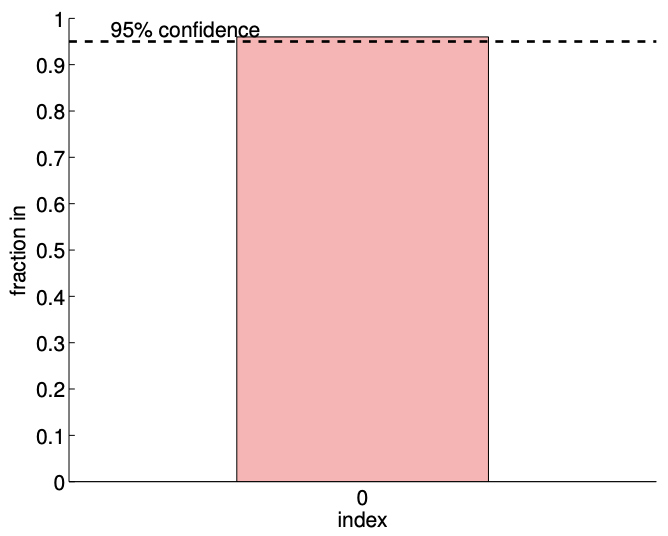
Los resultados del ajuste de mínimos cuadrados para\(m=14\) y\(m=140\) se muestran en la Figura\(19.2\). Aquí\(y_{\text {clean }}\) corresponde a los datos libres de ruido,\(y_{\text {clean }}=1 / 2\). La convergencia del intervalo de\(95 \%\) confianza con el número de muestras se representa en la Figura\(19.3(\mathrm{a})\). Destacamos que para el propósito de estas figuras y posteriormente figuras similares trazamos los intervalos de confianza desplazados por\(\beta_{0}^{\text {true }}\). No sabríamos\(\beta_{0}^{\text {true }}\) en la práctica, sin embargo estas cifras pretenden demostrar el desempeño de los intervalos de confianza en un caso en el que efectivamente se conocen los valores verdaderos. Cada una de las realizaciones de los intervalos de confianza incluye el valor del parámetro verdadero. De hecho, para el\(m=140\) caso, la Figura\(19.3(\mathrm{~b})\) muestra que 96 de cada 100 realizaciones del intervalo de confianza incluyen el valor del parámetro verdadero, que es consistente con el nivel de\(95 \%\) confianza para el intervalo. (Por supuesto que en la práctica solo calcularíamos un único intervalo de confianza).

(a) intervalos de confianza\(95 \%\) cambiados

b)\(95 \% \mathrm{ci}\) entrada/salida (100 realizaciones,\(m=140)\)

Figura 19.3: (a) La variación en el intervalo de\(95 \%\) confianza con el tamaño de muestreo\(m\) para el ajuste constante del modelo. b) La frecuencia del intervalo de confianza\(I_{0}\), incluido el parámetro verdadero\(\beta_{0}^{\text {true }} .\)

Ejemplo 19.1.3 Modelo de regresión constante y su relación con el análisis determinista

Anteriormente, estudiamos cómo una perturbación de datos\(g-g_{0}\) afecta la solución de mínimos cuadrados\(z^{*}-z_{0}\). En el análisis asumimos que existe una solución única\(z_{0}\) al problema limpio,\(B z_{0}=g_{0}\), y luego comparamos la solución con la solución\(z^{*}\) de mínimos cuadrados al problema perturbado,\(B z^{*}=g\). Al igual que en el análisis anterior, usamos el subíndice 0 para representar el superíndice “verdadero” para desordenar la notación.

Ahora consideremos un contexto estadístico, donde la perturbación en el lado derecho es inducida por la distribución normal de media cero con varianza\(\sigma^{2}\). En este caso,\[\frac{1}{m} \sum_{i=1}^{m}\left(g_{0, i}-g_{i}\right)\] es la media muestral de la distribución normal, en la que esperamos incurrir en fluctuaciones del orden de\(\sigma / \sqrt{m}\). Es decir, la desviación en la solución es\[z_{0}-z^{*}=\left(B^{\mathrm{T}} B\right)^{-1} B^{\mathrm{T}}\left(g_{0}-g\right)=m^{-1} \sum_{i=1}^{m}\left(g_{0, i}-g_{i}\right)=\mathcal{O}\left(\frac{\sigma}{\sqrt{m}}\right)\] Note que esta convergencia es más rápida que la obtenida directamente de los límites de perturbación anteriores,\[\left|z_{0}-z^{*}\right| \leq \frac{1}{\sqrt{m}}\left\|g_{0}-g\right\|=\frac{1}{\sqrt{m}} \sqrt{m} \sigma=\sigma\] lo que sugiere que el error no convergería. La diferencia sugiere que la perturbación resultante del ruido normal es diferente de cualquier perturbación arbitraria. En particular, recordemos que el encuadernado determinista basado en la desigualdad Cauchy-Schwarz es pesimista cuando la perturbación no está bien alineada con\(\operatorname{col}(B)\), lo cual es una constante. En el contexto estadístico, el ruido\(g_{0}-g\) es relativamente ortogonal al espacio de la columna\(\operatorname{col}(B)\), lo que resulta en una convergencia más rápida que para una perturbación arbitraria.

(a)\(m=14\)

b)\(m=140\)

Figura 19.4: Ajuste de mínimos cuadrados de una función lineal utilizando un modelo lineal.

Ejemplo 19.1.4 Estimación de mínimos cuadrados para un modelo lineal

Como segundo ejemplo, considere una función aleatoria de la forma\[Y(x) \sim-\frac{1}{2}+\frac{2}{3} x+\mathcal{N}\left(0, \sigma^{2}\right),\] con la varianza\(\sigma^{2}=0.01\). El objetivo es modelar la función usando un modelo lineal\[Y_{\text {model }}(x ; \beta)=\beta_{0}+\beta_{1} x\] donde los parámetros\(\left(\beta_{0}, \beta_{1}\right)\) se encuentran a través del ajuste de mínimos cuadrados. Tenga en cuenta que los verdaderos parámetros están dados por\(\beta_{0}^{\text {true }}=-1 / 2\) y\(\beta_{1}^{\text {true }}=2 / 3\). Como en el caso del modelo constante, tomamos medidas en siete puntos,\(x=0,0.5,1.0, \ldots, 3.0\); en cada punto tomamos\(n_{\text {sample measurements for the total }}\)\(m=7 \cdot n_{\text {sample }}\) medidas. Aquí, es importante que tomemos medidas en al menos dos\(x\) ubicaciones diferentes; de lo contrario, la matriz\(B\) será singular. Esto tiene sentido porque si elegimos solo una\(x\) ubicación estamos tratando de encajar efectivamente una línea a través de un solo punto, lo cual es un problema mal planteado.

Los resultados del ajuste de mínimos cuadrados para\(m=14\) y\(m=140\) se muestran en la Figura\(19.4\). Vemos que el ajuste se vuelve más ajustado a medida que aumenta el número de muestras\(m\),,.

También podemos cuantificar la calidad de la estimación de parámetros en términos de los intervalos de confianza. La convergencia del intervalo de\(95 \%\) confianza individual con el número de muestras se representa en la Figura\(19.5(\mathrm{a})\). Recordemos que los intervalos de confianza individuales\(I_{i}, i=0,1\),, se construyen para satisfacer\[P\left(\beta_{0}^{\text {true }} \in I_{0}\right)=\gamma \quad \text { and } \quad P\left(\beta_{1}^{\text {true }} \in I_{1}\right)=\gamma\] con el nivel de confianza\(\gamma(95 \%\) para este caso) utilizando la\(t\) distribución del Estudiante. Claramente, cada uno de los intervalos de confianza individuales se vuelve más ajustado a medida que tomamos más medidas y mejora nuestra confianza en nuestra estimación de parámetros. Obsérvese que la realización de intervalos de confianza incluye el valor de parámetro verdadero para cada uno de los tamaños de muestra considerados.

(a) intervalos de confianza\(95 \%\) cambiados

b)\(95 \% \mathrm{ci}\) entrada/salida (1000 realizaciones,\(m=140)\)

Figura 19.5: a) La variación en el intervalo de\(95 \%\) confianza con el tamaño de muestreo\(m\) para el ajuste del modelo lineal. b) La frecuencia de los intervalos de confianza individuales\(I_{0}\) e\(I_{1}\) incluyendo los parámetros verdaderos \(\beta_{0}^{\text {true }}\)y\(\beta_{1}^{\text {true }}\left(0\right.\) y 1, respectivamente), y\(I_{0}^{\text {joint }} \times I_{1}^{\text {joint }}\) conjuntamente incluyendo (\(\left.\beta_{0}^{\text {true }}, \beta_{1}^{\text {true }}\right)\)(todos).

Podemos verificar la validez de los intervalos de confianza individuales midiendo la frecuencia con la que cada uno de los parámetros verdaderos se encuentra en el intervalo correspondiente para un gran número de realizaciones. El resultado para 1000 realizaciones se muestra en la Figura 19.5 (b). La columna indexada “0" corresponde a la frecuencia de\(\beta_{0}^{\text {true }} \in I_{0}\), y la columna indexada “1" corresponde a la frecuencia de\(\beta_{1}^{\text {true }} \in I_{1}\). Según lo diseñado, cada uno de los intervalos de confianza individuales incluye el verdadero parámetro\(\gamma=95 \%\) de los tiempos.

También podemos verificar la validez del intervalo de confianza conjunta midiendo la frecuencia en la que los parámetros toman\(\left(\beta_{1}, \beta_{2}\right)\) conjuntamente los valores dentro\(I_{0}^{\text {joint }} \times I_{1}^{\text {joint }}\). Recordemos que nuestros intervalos conjuntos están diseñados para satisfacer\[P\left(\beta_{0}^{\text {true }} \in I_{0}^{\text {joint }} \text { and } \beta_{1}^{\text {true }} \in I_{1}^{\text {joint }}\right) \geq \gamma\] y utiliza la\(F\) -distribución. La columna indexada “todos” en la Figura 19.5 (b). corresponde a la frecuencia que\(\left(\beta_{0}^{\text {true }}, \beta_{1}^{\text {true }}\right) \in I_{0}^{\text {joint }} \times I_{1}^{\text {joint }}\). Tenga en cuenta que la tasa de éxito conjunto es ligeramente\((\approx 97 \%)\) mayor que\(\gamma\) ya que los intervalos de confianza que proporcionamos son un límite simple pero conservador para la región de confianza elíptica real. Por otro lado, si usamos erróneamente los intervalos de confianza individuales en lugar del intervalo de confianza conjunto, los intervalos de confianza individuales son demasiado pequeños e incluyen conjuntamente los parámetros verdaderos solo\(\approx 92 \%\) del tiempo. Por lo tanto, enfatizamos que es importante construir intervalos de confianza que sean apropiados para la cuestión de interés.

Prueba de Hipótesis

También podemos, en lugar de nuestros CI (o de hecho, basados en nuestros CI), considerar una hipótesis sobre los parámetros, y luego probar estas hipótesis. Por ejemplo, en este último ejemplo, podríamos desear probar la hipótesis (conocida como la hipótesis nula) que\(\beta_{0}^{\text {true }}=0\). Consideramos Ejemplo 19.1.4 para el caso en el que\(m=1400\). Claramente, nuestro CI no incluye\(\beta_{0}^{\text {true }}=0\). Así lo más probable\(\beta_{0}^{\text {true }} \neq 0\), y rechazamos la hipótesis. En general, rechazamos la hipótesis cuando el IC no incluye cero.

Podemos analizar fácilmente el error Tipo I, que se define como la probabilidad de que rechacemos la hipótesis cuando la hipótesis es de hecho cierta. Asumimos que la hipótesis es cierta. Entonces, la probabilidad de que el CI no incluya cero -y de ahí que rechacemos la hipótesis- es\(0.05\), ya que sabemos que\(95 \%\) del tiempo nuestro CI incluirá cero - el verdadero valor bajo nuestra hipótesis. (Esto se puede reformular en términos de un estadístico de prueba y una región crítica para el rechazo). Denotamos por\(0.05\) el “tamaño” de la prueba, la probabilidad de que rechacemos incorrectamente la hipótesis debido a una “fluctuación” desafortunada (rara).

También podemos introducir la noción de error Tipo II, que se define como la probabilidad de que aceptemos la hipótesis cuando la hipótesis es de hecho falsa. Y el “poder” de la prueba es la probabilidad de que rechacemos la hipótesis cuando la hipótesis de hecho falsa: la potencia es 1 - el error Tipo II. Por lo general, es más difícil calcular los errores de Tipo II (y la potencia) que los errores de Tipo I.

Inspección de Supuestos

Al estimar los parámetros para el modelo de respuesta y construir los intervalos de confianza correspondientes, nos basamos en los supuestos de ruido (N1), (N2) y (N3). En esta sección, consideramos ejemplos que ilustran cómo se pueden romper los supuestos. Luego, proponemos métodos para verificar la verosimilitud de los supuestos. Tenga en cuenta que damos aquí algunas pruebas bastante simples sin ninguna estructura estadística subyacente; de hecho, es posible ser más rigurosos sobre cuándo aceptar o rechazar nuestras hipótesis de ruido y sesgo introduciendo estadísticas apropiadas de tal manera que se puedan cuantificar “pequeños” y “grandes”. (También es posible perseguir directamente nuestra estimación de parámetros bajo supuestos de ruido más generales).

Comprobación de la plausibilidad de los supuestos de ruido

Consideremos un sistema gobernado por una función afín aleatoria, pero supongamos que el ruido\(\epsilon(x)\) está perfectamente correlacionado en\(x\). Es decir,\[Y\left(x_{i}\right)=\beta_{0}^{\text {true }}+\beta_{1}^{\text {true }} x_{i}+\epsilon\left(x_{i}\right),\] donde A\[\epsilon\left(x_{1}\right)=\epsilon\left(x_{2}\right)=\cdots=\epsilon\left(x_{m}\right) \sim \mathcal{N}\left(0, \sigma^{2}\right) .\] pesar de que se cumplen los supuestos (N1) y (N2), en este caso se viola el supuesto de independencia, (N3). Debido a que el error sistemático desplaza la salida en una constante, el coeficiente de la solución de mínimos cuadrados correspondiente a la función constante\(\beta_{0}\) sería desplazado por el error. Aquí, el ruido (perfectamente correlacionado)\(\epsilon\) se interpreta incorrectamente como señal.

Presentemos ahora una prueba para verificar la plausibilidad de los supuestos, que detectaría la presencia del escenario anterior (entre otros). La verificación se puede lograr muestreando el sistema de manera controlada. Digamos que recolectamos\(N\) muestras evaluadas en\(x_{L}\),\[L_{1}, L_{2}, \ldots, L_{N} \quad \text { where } \quad L_{i}=Y\left(x_{L}\right), \quad i=1, \ldots, N .\] De igual manera, recogemos otro conjunto de\(N\) muestras evaluadas en\(x_{R} \neq x_{L}\),\[R_{1}, R_{2}, \ldots, R_{N} \quad \text { where } \quad R_{i}=Y\left(x_{R}\right), \quad i=1, \ldots, N .\] Usando las muestras, primero calculamos la estimación para la media y varianza para \(L\),\[\hat{\mu}_{L}=\frac{1}{N} \sum_{i=1}^{N} L_{i} \quad \text { and } \quad \hat{\sigma}_{L}^{2}=\frac{1}{N-1} \sum_{i=1}^{N}\left(L_{i}-\hat{\mu}_{L}\right)^{2},\] y los de\(R\),\[\hat{\mu}_{R}=\frac{1}{N} \sum_{i=1}^{N} R_{i} \quad \text { and } \quad \hat{\sigma}_{R}^{2}=\frac{1}{N-1} \sum_{i=1}^{N}\left(R_{i}-\hat{\mu}_{R}\right)^{2} .\] Para verificar la suposición de normalidad (N1), podemos trazar el histograma para\(L\) y\(R\) (usando un número apropiado de bins) y para\(\mathcal{N}\left(\hat{\mu}_{L}, \hat{\sigma}_{L}^{2}\right)\) y\(\mathcal{N}\left(\hat{\mu}_{R}, \hat{\sigma}_{R}^{2}\right)\). Si el error se distribuye normalmente, estos histogramas deben ser similares, y parecerse a la distribución normal. De hecho, existen pruebas estadísticas mucho más rigurosas y cuantitativas para evaluar si los datos derivan de una población particular (aquí normal).

Para verificar el supuesto de homocedasticidad (N2), podemos comparar la estimación de varianza para muestras\(L\) y\(R\), es decir,\(\hat{\sigma}_{L}^{2} \approx \hat{\sigma}_{R}^{2}\) ¿es? Si\(\hat{\sigma}_{L}^{2} \approx \hat{\sigma}_{R}^{2}\), entonces la suposición (N2) no es probable que sea plausible porque el ruido en\(x_{L}\) y\(x_{R}\) tienen diferentes distribuciones.

Finalmente, para verificar la suposición de no correlación (N3), podemos verificar el coeficiente de correlación\(\rho_{L, R}\) entre\(L\) y\(R\). El coeficiente de correlación se estima como\[\hat{\rho}_{L, R}=\frac{1}{\hat{\sigma}_{L} \hat{\sigma}_{R}} \frac{1}{N-1} \sum_{i=1}^{N}\left(L_{i}-\hat{\mu}_{L}\right)\left(R_{i}-\hat{\mu}_{R}\right) .\] Si el coeficiente de correlación no es cercano a 0, entonces la suposición (N3) no es probable que sea plausible. En el ejemplo considerado con el ruido correlacionado, nuestro sistema fallaría esta última prueba.

Comprobación de la presencia de sesgo

Consideremos nuevamente un sistema gobernado por una función afín. Esta vez, asumimos que el sistema está libre de ruido, es decir,\[Y(x)=\beta_{0}^{\text {true }}+\beta_{1}^{\text {true }} x\] modelaremos el sistema usando una función constante,\[Y_{\text {model }}=\beta_{0} .\] Debido a que nuestro modelo constante coincidiría con la media de la distribución subyacente, interpretaríamos\(Y\) - media\((Y)\) como el error. En este caso, la señal se interpreta como un ruido.

Podemos verificar la presencia de sesgo comprobando si\[\left|\hat{\mu}_{L}-\widehat{Y}_{\text {model }}\left(x_{L}\right)\right| \sim \mathcal{O}(\hat{\sigma}) .\] si la relación no se sostiene, entonces indica una falta de ajuste, es decir, la presencia de sesgo. Tenga en cuenta que la replicación, así como la exploración de datos de manera más general, es crucial para comprender los supuestos. Nuevamente, existen pruebas estadísticas (digamos, hipótesis) mucho más rigurosas y cuantitativas para evaluar si hay sesgo presente.