19.2: Caso General

Consideramos un caso más general de regresión, en el que no nos limitamos a un modelo de respuesta lineal. Sin embargo, seguimos asumiendo que los supuestos de ruido (N1), (N2) y (N3) se mantienen.

Modelo de respuesta

Considere una relación general entre la medición\(Y\), el modelo\(Y_{\text {model }}\) de respuesta y el ruido\(\epsilon\) de la forma\[Y(x)=Y_{\text {model }}(x ; \beta)+\epsilon,\] donde la variable independiente\(x\) es valorada vectorialmente con\(p\) componentes, i.e. \[x=\left(x_{(1)}, x_{(2)}, \cdots, x_{(p)}\right)^{\mathrm{T}} \in D \subset \mathbb{R}^{p} .\]El modelo de respuesta es de la forma\[Y_{\text {model }}(x ; \beta)=\beta_{0}+\sum_{j=1}^{n-1} \beta_{j} h_{j}(x),\] donde\(h_{j}, j=0, \ldots, n-1\), son las funciones base y\(\beta_{j}, j=0, \ldots, n-1\), son los coeficientes de regresión. Tenga en cuenta que hemos elegido\(h_{0}(x)=1\). Similar al caso afín, asumimos que\(Y_{\text {model }}\) es suficientemente rico (con respecto a la función aleatoria subyacente\(Y\)), tal que existe un parámetro\(\beta^{\text {true }}\) con el que describe\(Y_{\text {model }}\left(\cdot ; \beta^{\text {true }}\right)\) perfectamente el comportamiento del ruido- función subyacente libre, es decir, imparcial. (Equivalentemente, existe\(\beta^{\text {true }}\) tal que\(Y(x) \sim \mathcal{N}\left(Y_{\text {model }}\left(x ; \beta^{\text {true }}\right), \sigma^{2}\right)\).

Es importante señalar que esta sigue siendo una regresión lineal. Es lineal en el sentido de que los coeficientes de regresión\(\beta_{j}, j=0, \ldots, n-1\), aparecen linealmente en\(Y_{\text {model }}\). Las funciones base\(h_{j}\),\(j=0, \ldots, n-1\), no necesitan ser lineales en\(x\); por ejemplo,\(h_{1}\left(x_{(1)}, x_{(2)}, x_{(3)}\right)=x_{(1)} \exp \left(x_{(2)} x_{(3)}\right)\) es perfectamente aceptable para una función base. El caso simple considerado en el apartado anterior corresponde a\(p=1, n=2\), con\(h_{0}(x)=1\) y\(h_{1}(x)=x\).

Hay dos enfoques principales para elegir las funciones base.

(i) Funciones derivadas del comportamiento anticipado basado en modelos físicos. Por ejemplo, para deducir el coeficiente de fricción, podemos relacionar la fricción estática y la fuerza normal siguiendo las leyes de fricción de Amontones y Coulomb,\[F_{\mathrm{f}, \text { static }}=\mu_{\mathrm{s}} F_{\text {normal, applied }}\] donde\(F_{\mathrm{f}, \text { static }}\) está la fuerza de fricción,\(\mu_{\mathrm{s}}\) es el coeficiente de fricción y la\(F_{\text {normal, applied is the normal }}\) fuerza. Señalando que\(F_{\mathrm{f} \text {, static }}\) es una función lineal de\(F_{\text {normal, applied, we can choose a linear basis }}\) función\(h_{1}(x)=x\).

Aunque podemos elegir\(n\) grandes y dejar que los mínimos cuadrados encuentren el\(\operatorname{good} \beta\) -el buen modelo dentro de nuestra expansión general- esto no suele ser una buena idea: para evitar el sobreajuste, debemos asegurarnos de que el número de experimentos sea mucho mayor que el orden del modelo, es decir, \(m \gg n\). Volvemos al sobreajuste más adelante en el capítulo.

Estimación

Tomamos\(m\) medidas para recolectar pares\(m\) independientes de medición variable\[\left(x_{i}, Y_{i}\right), \quad i=1, \ldots, m,\] donde\(x_{i}=\left(x_{(1)}, x_{(2)}, \ldots, x_{(p)}\right)_{i}\). Afirmamos\[\begin{aligned} Y_{i} &=Y_{\text {model }}\left(x_{i} ; \beta\right)+\epsilon_{i} \\ &=\beta_{0}+\sum_{j=1}^{n-1} \beta_{j} h_{j}\left(x_{i}\right)+\epsilon_{i}, \quad i=1, \ldots, m, \end{aligned}\] qué rendimientos\[\underbrace{\left(\begin{array}{c} Y_{1} \\ Y_{2} \\ \vdots \\ Y_{m} \end{array}\right)}_{Y}=\underbrace{\left(\begin{array}{ccccc} 1 & h_{1}\left(x_{1}\right) & h_{2}\left(x_{1}\right) & \ldots & h_{n-1}\left(x_{1}\right) \\ 1 & h_{1}\left(x_{2}\right) & h_{2}\left(x_{2}\right) & \ldots & h_{n-1}\left(x_{2}\right) \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 1 & h_{1}\left(x_{m}\right) & h_{2}\left(x_{m}\right) & \ldots & h_{n-1}\left(x_{m}\right) \end{array}\right)}_{X} \underbrace{\left(\begin{array}{c} \beta_{0} \\ \beta_{1} \\ \vdots \\ \beta_{n-1} \end{array}\right)}_{\beta}+\underbrace{\left(\begin{array}{c} \epsilon\left(x_{1}\right) \\ \epsilon\left(x_{2}\right) \\ \vdots \\ \epsilon\left(x_{m}\right) \end{array}\right)}_{\epsilon} .\] El estimador de mínimos cuadrados viene dado por\[\left(X^{\mathrm{T}} X\right) \hat{\beta}=X^{\mathrm{T}} Y,\] y\(\hat{\beta}\) se mide la bondad de ajuste por\(\hat{\sigma}\),\[\hat{\sigma}=\left(\frac{1}{m-n}\|Y-\widehat{Y}\|^{2}\right)^{1 / 2},\] donde\[\widehat{Y}=\left(\begin{array}{c} \widehat{Y}_{\text {model }}\left(x_{1}\right) \\ \widehat{Y}_{\text {model }}\left(x_{2}\right) \\ \vdots \\ \widehat{Y}_{\text {model }}\left(x_{m}\right) \end{array}\right)=\left(\begin{array}{c} \hat{\beta}_{0}+\sum_{j=1}^{n-1} \hat{\beta}_{j} h_{j}\left(x_{1}\right) \\ \hat{\beta}_{0}+\sum_{j=1}^{n-1} \hat{\beta}_{j} h_{j}\left(x_{2}\right) \\ \vdots \\ \hat{\beta}_{0}+\sum_{j=1}^{n-1} \hat{\beta}_{j} h_{j}\left(x_{m}\right) \end{array}\right)=X \hat{\beta} .\] Como antes, la media de la media del modelo es igual a la media de las mediciones, i.e. \[\overline{\widehat{Y}}=\bar{Y}\]donde\[\overline{\widehat{Y}}=\frac{1}{m} \sum_{i=1}^{m} \widehat{Y}_{i} \text { and } \bar{Y}=\frac{1}{m} \sum_{i=1}^{m} Y_{i} .\] La preservación de la media está garantizada por la presencia del término constante\(\beta_{0} \cdot 1\) en nuestro modelo.

Intervalos de confianza

La construcción de los intervalos de confianza sigue el procedimiento desarrollado en el apartado anterior. Definamos la matriz de covarianza\[\widehat{\Sigma}=\hat{\sigma}^{2}\left(X^{\mathrm{T}} X\right)^{-1}\] Entonces, los intervalos de confianza individuales están dados por\[I_{j}=\left[\hat{\beta}_{j}-t_{\gamma, m-n} \sqrt{\widehat{\Sigma}_{j+1, j+1}}, \hat{\beta}_{j}+t_{\gamma, m-n} \sqrt{\widehat{\Sigma}_{j+1, j+1}}\right], \quad j=0, \ldots, n-1,\] donde\(t_{\gamma, m-n}\) viene de la\(t\) distribución de Student como antes, es decir,\[t_{\gamma, m-n}=F_{T, m-n}^{-1}\left(\frac{1}{2}+\frac{\gamma}{2}\right),\] dónde\(F_{T, q}^{-1}\) está la función de distribución acumulativa inversa de la\(t\) -distribución. El desplazamiento de los índices de la matriz de covarianza se debe al índice para los parámetros a partir de 0 y al índice para la matriz a partir de 1. Cada uno de los intervalos de confianza individual satisface\[P\left(\beta_{j}^{\text {true }} \in I_{j}\right)=\gamma, \quad j=0, \ldots, n-1,\] dónde\(\gamma\) está el nivel de confianza.

También podemos desarrollar intervalos de confianza conjunta,\[I_{j}^{\text {joint }}=\left[\hat{\beta}_{j}-s_{\gamma, n, m-n} \sqrt{\widehat{\Sigma}_{j+1, j+1}}, \hat{\beta}_{j}+s_{\gamma, n, m-n} \sqrt{\widehat{\Sigma}_{j+1, j+1}}\right], \quad j=0, \ldots, n-1,\] donde el parámetro\(s_{\gamma, n, m-n}\) se calcula a partir de la función de distribución acumulativa inversa para la\(F\) -distribución de acuerdo con\[s_{\gamma, n, m-n}=\sqrt{n F_{F, n, m-n}^{-1}(\gamma)} .\] Los intervalos de confianza conjunta satisfacen\[P\left(\beta_{0}^{\text {true }} \in I_{0}^{\text {joint }}, \beta_{1}^{\text {true }} \in I_{1}^{\text {joint }}, \ldots, \beta_{n-2}^{\text {true }} \in I_{n-2}^{\text {joint }}, \text { and } \beta_{n-1}^{\text {true }} \in I_{n-1}^{\text {joint }}\right) \geq \gamma .\]

Ejemplo 19.2.1 Estimación de mínimos cuadrados para una función cuadrática

Considera una función aleatoria de la forma\[Y(x) \sim-\frac{1}{2}+\frac{2}{3} x-\frac{1}{8} x^{2}+\mathcal{N}\left(0, \sigma^{2}\right),\] con la varianza\(\sigma^{2}=0.01\). Nos gustaría modelar el comportamiento de la función. Supongamos que sabemos (aunque sea una ley física o experiencia) que la salida del proceso subyacente depende cuadráticamente de la entrada\(x\). Así, elegimos las funciones base\[h_{1}(x)=1, \quad h_{2}(x)=x, \quad \text { and } \quad h_{3}(x)=x^{2} .\] El modelo resultante es de la forma\[Y_{\text {model }}(x ; \beta)=\beta_{0}+\beta_{1} x+\beta_{2} x^{2},\]

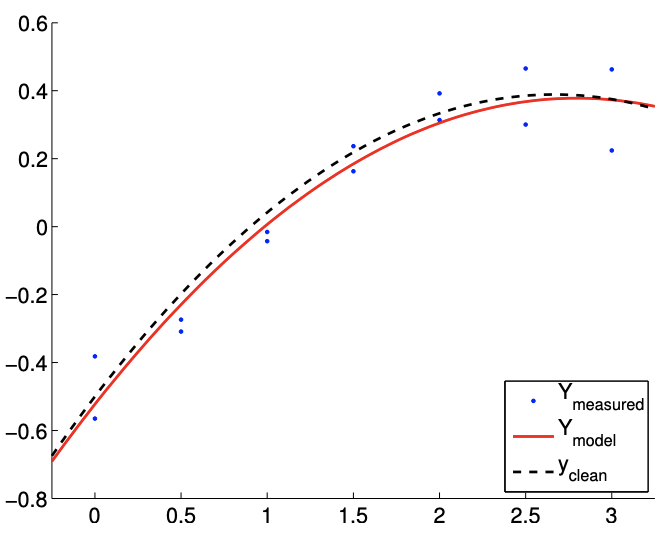
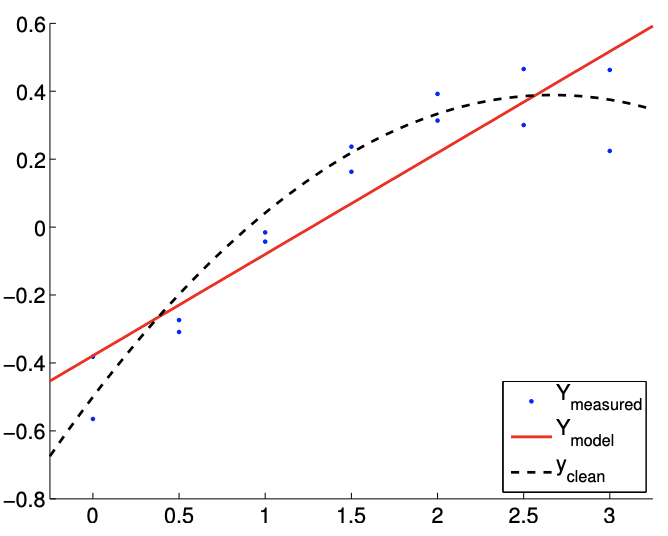
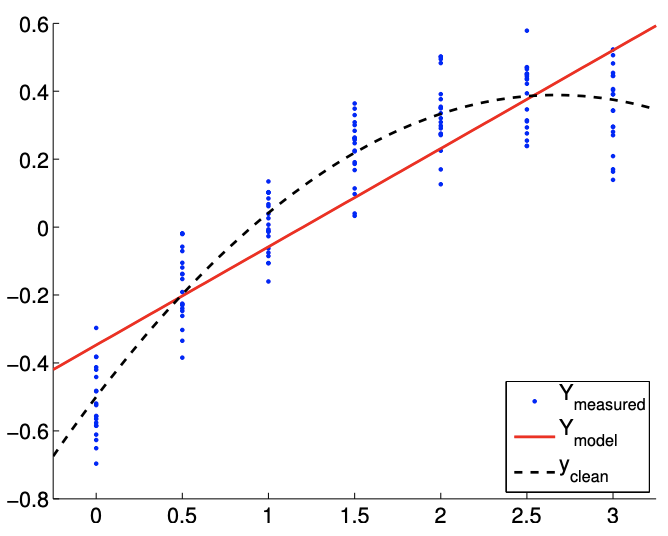
(a)\(m=14\)

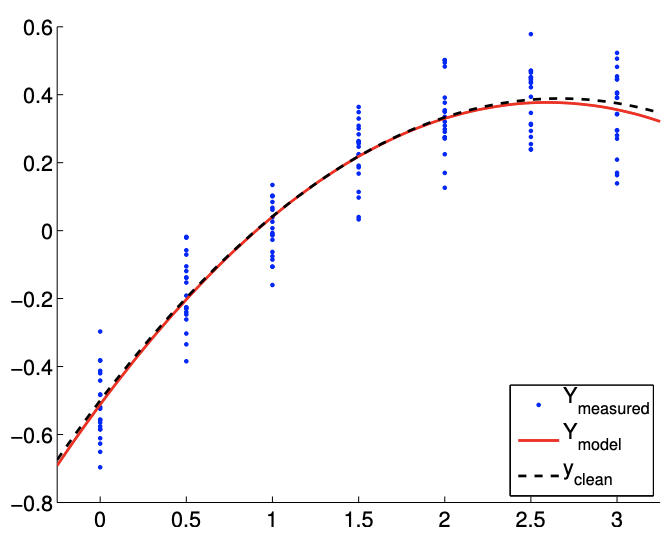
b)\(m=140\)

Figura 19.6: Ajuste de mínimos cuadrados de una función cuadrática utilizando un modelo cuadrático.

donde\(\left(\beta_{0}, \beta_{1}, \beta_{2}\right)\) están los parámetros a determinar a través del ajuste de mínimos cuadrados. Tenga en cuenta que los verdaderos parámetros vienen dados por\(\beta_{0}^{\text {true }}=-1 / 2, \beta_{1}^{\text {true }}=2 / 3\), y\(\beta_{2}^{\text {true }}=-1 / 8\).

El resultado del cálculo se muestra en la Figura 19.6. Nuestro modelo coincide cualitativamente con el modelo subyacente “verdadero”. La figura\(19.7(\mathrm{a})\) muestra que el intervalo de confianza\(95 \%\) individual para cada uno de los parámetros converge a medida que aumenta el número de muestras.

La Figura 19.7 (b) verifica que los intervalos de confianza individuales incluyen el parámetro verdadero aproximadamente\(95 \%\) de los tiempos (mostrado en las columnas indexadas 0,1, y 2). Nuestro intervalo de confianza conjunta también incluye conjuntamente el verdadero parámetro acerca\(98 \%\) de los tiempos, que es mayor que el nivel de confianza prescrito de\(95 \%\). (Tenga en cuenta que los intervalos de confianza individuales incluyen conjuntamente los parámetros verdaderos solo aproximadamente\(91 \%\) de los tiempos). Estos resultados confirman que tanto los intervalos de confianza individuales como los conjuntos son indicadores confiables de la calidad de las estimaciones respectivas.

Overfitting (y Underfitting)

Hemos discutido la importancia de elegir un modelo con un tamaño suficientemente grande\(n-\) como para que la verdadera distribución subyacente sea representable y no habría sesgo -pero también se insinuó que\(n\) mucho más grande de lo necesario puede resultar en un sobreajuste de los datos. El sobreajuste degrada significativamente la calidad de nuestra estimación de parámetros y modelo predictivo, especialmente cuando los datos son ruidosos o el número de puntos de datos es pequeño. Ilustremos el efecto del sobreajuste usando algunos ejemplos.

Ejemplo 19.2.2 sobreajuste de una función lineal

Consideremos una función lineal ruidosa\[Y(x) \sim \frac{1}{2}+2 x+\mathcal{N}\left(0, \sigma^{2}\right) .\] Sin embargo, a diferencia de los ejemplos anteriores, asumimos que no conocemos la forma de la dependencia inputoutput. En este y en los dos siguientes ejemplos, consideraremos un ajuste polinómico de\(n-1\) grado general de la forma\[Y_{\text {model }, n}(x ; \beta)=\beta_{0}+\beta_{1} x^{1}+\cdots+\beta_{n-1} x^{n-1} .\]

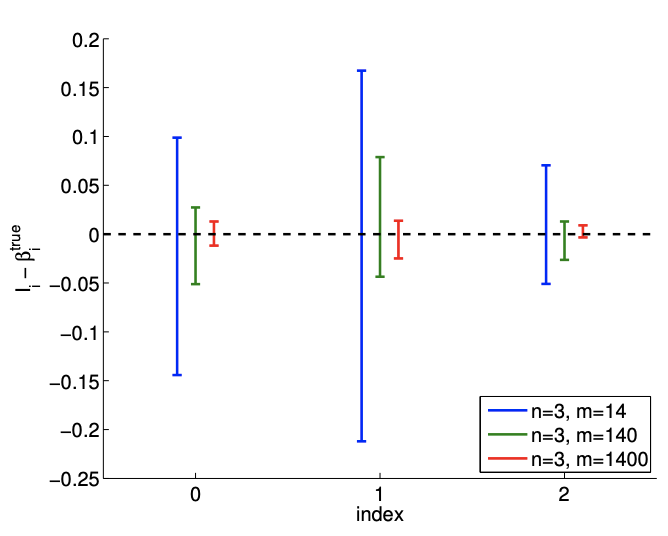
a) intervalos de confianza\(95 \%\) desplazados

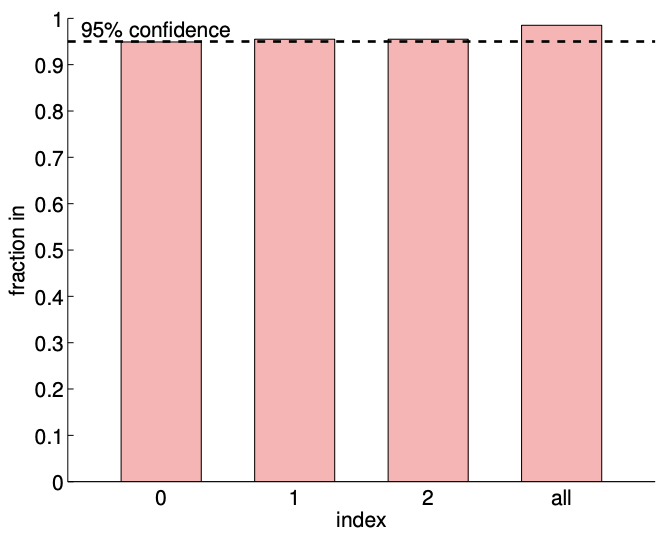
b)\(95 \% \mathrm{ci}\) entrada/salida (1000 realizaciones,\(m=140)\)

Figura 19.7: (a) La variación en el intervalo de\(95 \%\) confianza con el tamaño de muestreo\(m\) para el ajuste del modelo lineal. b) La frecuencia de los intervalos de confianza individuales\(I_{0}, I_{1}\), e\(I_{2}\) incluyendo los parámetros verdaderos\(\beta_{0}^{\text {true }}, \beta_{1}^{\text {true }}\), y\(\beta_{2}^{\text {true }}\left(0,1\right.\), y 2, respectivamente), y\(I_{0}^{j \text { joint }} \times I_{1}^{\text {joint }} \times I_{2}^{\text {joint }}\) conjuntamente incluyendo\(\left(\beta_{0}^{\text {true }}, \beta_{1}^{\text {true }}, \beta_{2}^{\text {true }}\right)\) (todos).

Tenga en cuenta que los verdaderos parámetros para la función ruidosa son\[\beta_{0}^{\text {true }}=\frac{1}{2}, \quad \beta_{1}^{\text {true }}=2, \quad \text { and } \quad \beta_{2}^{\text {true }}=\cdots=\beta_{n}^{\text {true }}=0\] para cualquiera\(n \geq 2\).

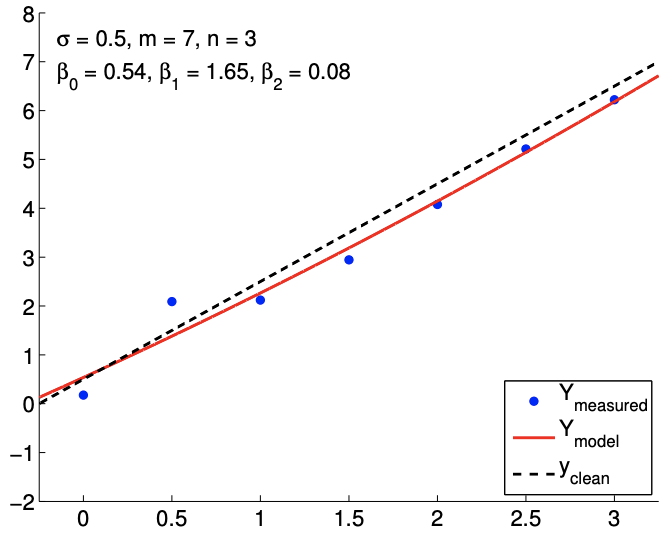
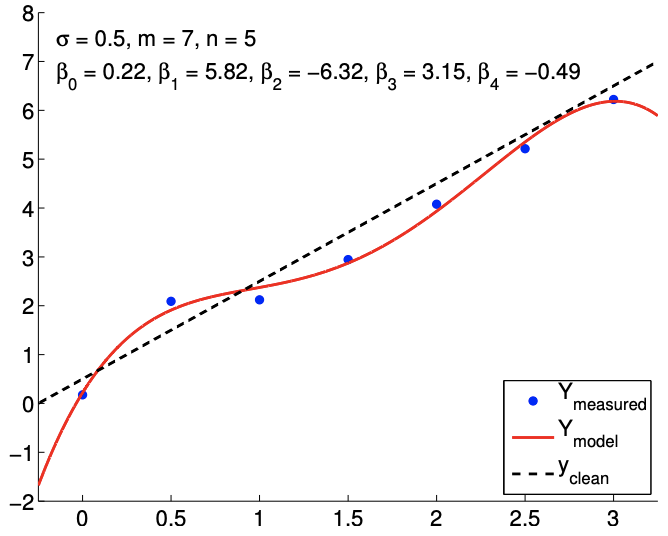
Los resultados del ajuste de la función lineal ruidosa utilizando\(m=7\) mediciones para los modelos\(n=2, n=3\), y\(n=5\) respuesta se muestran en la Figura\(19.8(\mathrm{a}),(\mathrm{b})\), y\((\mathrm{c})\), respectivamente. El\(n=2\) es el caso nominal, que coincide con la verdadera dependencia funcional subyacente, y los\(n=5\) casos\(n=3\) y corresponden a casos de sobreajuste. Para cada ajuste, también indicamos la estimación de mínimos cuadrados de los parámetros. Cualitativamente, vemos que el error de predicción,\(y_{\text {clean }}(x)-Y_{\text {model }}(x)\), es mayor para el modelo cuártico\((n=5)\) que para el modelo afín\((n=2)\). En particular, debido a que el modelo cuártico está ajustando cinco parámetros usando solo siete puntos de datos, el modelo está cerca de interpolar el ruido, resultando en un comportamiento oscilatorio que sigue al ruido. Esta oscilación se vuelve más pronunciada a medida que aumenta el nivel de ruido\(\sigma\),,.

En cuanto a estimar los parámetros\(\beta_{0}^{\text {true }}\) y\(\beta_{1}^{\text {true }}\), el modelo afín vuelve a funcionar mejor que los casos de sobreajuste. En particular, el error en\(\hat{\beta}_{1}\) es más de un orden de magnitud mayor para el\(n=5\) modelo que para el\(n=2\) modelo. Afortunadamente, esta inexactitud en la estimación del parámetro se refleja en grandes intervalos de confianza, como se muestra en la Figura\(19.9\). Los intervalos de confianza son válidos porque nuestros modelos con\(n \geq 2\) son capaces de representar la dependencia funcional subyacente con\(n^{\text {true }}=2\), y la suposición de falta de sesgo utilizada para construir los intervalos de confianza aún se mantiene. Así, si bien la estimación puede ser pobre, se nos informa que no debemos tener mucha confianza en nuestra estimación de los parámetros. Los grandes intervalos de confianza resultan del hecho de que el sobreajuste efectivamente no deja grados de libertad (o información) para estimar el ruido porque se utilizan relativamente demasiados grados de libertad para determinar los parámetros. En efecto, cuando\(m=n\), los intervalos de confianza son infinitos.

Debido a que el modelo es imparcial, más datos finalmente resuelven el mal ajuste, como se muestra en la Figura\(19.8(\mathrm{~d})\). Sin embargo, recordando que los intervalos de confianza convergen sólo como\(m{ }^{-1 / 2}\), una gran

(a)\(m=7, n=2\)

b)\(m=7, n=3\)

c)\(m=7, n=5\)

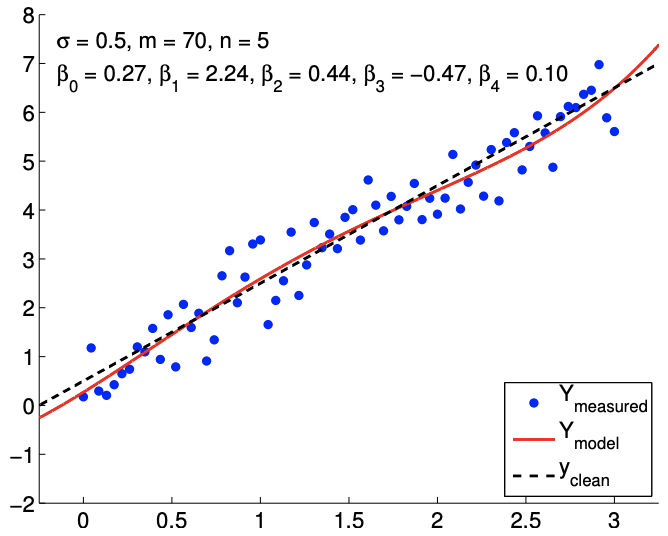
d)\(m=70, n=5\)

Figura 19.8: Ajuste de mínimos cuadrados de una función lineal utilizando modelos polinómicos de varios órdenes.

Figura 19.9: Intervalos de confianza\(95 \%\) desplazados para ajustar una función lineal utilizando modelos polinómicos de varios órdenes.

se requiere el número de muestras para ajustar los intervalos de confianza -y mejorar nuestras estimaciones de parámetros- para los casos de sobreajuste. Así, deducir un modelo de respuesta adecuado basado en, por ejemplo, principios físicos puede mejorar significativamente la calidad de las estimaciones de parámetros y el desempeño del modelo predictivo.

Comenzar material avanzado

Ejemplo 19.2.3 sobreajuste de una función cuadrática

En este ejemplo, estudiamos el efecto del sobreajuste con más detalle. Consideramos los datos gobernados por una función cuadrática aleatoria de la forma\[Y(x) \sim-\frac{1}{2}+\frac{2}{3} x-\frac{1}{8} c x^{2}+\mathcal{N}\left(0, \sigma^{2}\right),\] con\(c=1\). De nuevo consideramos para nuestro modelo la forma polinómica\(Y_{\text {model }, n}(x ; \beta)\).

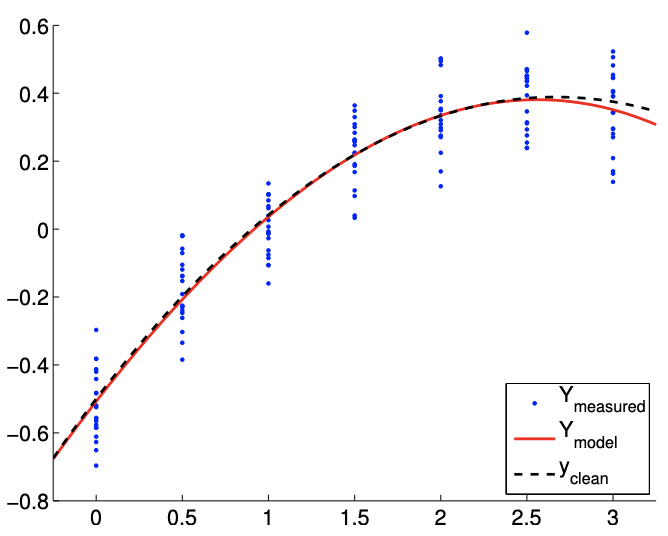
La Figura\(19.10\) (a) muestra un resultado típico del ajuste de los datos utilizando puntos de\(m=14\) muestreo y\(n=4\). Nuestro modelo cúbico incluye la distribución cuadrática subyacente. Por lo tanto, no hay sesgo y nuestros supuestos de ruido están satisfechos. Sin embargo, en comparación con el modelo cuadrático\((n=3)\), el modelo cúbico se ve afectado por el ruido en la medición y produce variaciones espurias. Esta variación espuria tiende a desaparecer con el número de puntos de muestreo, y la Figura\(19.10\) (b) con puntos de\(m=140\) muestreo muestra un ajuste más estable.

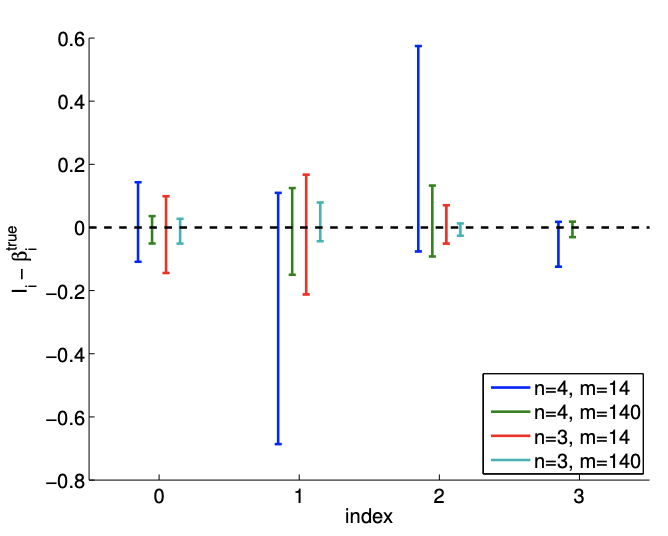
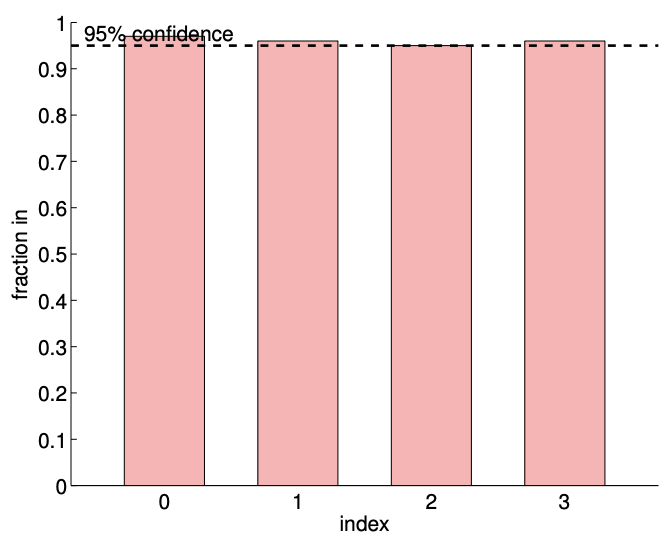
La figura\(19.10(\mathrm{c})\) muestra una realización de intervalos de confianza para el modelo cúbico\((n=4)\) utilizando\(m=14\) y puntos\(m=140\) de muestreo. También se muestra una realización de intervalos de confianza para el modelo cuadrático (\(n=3\)) para comparación. Usando el mismo conjunto de datos, los intervalos de confianza para el modelo cúbico son mayores que los del modelo cuadrático. Sin embargo, los intervalos de confianza del modelo cúbico incluyen el valor del parámetro verdadero para la mayoría de los casos. La figura\(19.10(\mathrm{~d})\) confirma que el\(95 \%\) de la realización de los intervalos de confianza incluye el parámetro verdadero. Así, los intervalos de confianza son indicadores confiables de la calidad de las estimaciones de parámetros, y en general los intervalos se vuelven más ajustados con\(m\), como se esperaba. El sobreajuste modesto,\(n=4\) vs.\(n=3\), con\(m\) suficientemente grande, plantea poca amenaza.

Comprobemos cómo el sobreajuste afecta la calidad del ajuste usando dos medidas diferentes. La primera es una medida de lo bien que podemos predecir, o reproducir, la función subyacente limpia; la segunda es una medida de qué tan bien aproximamos los parámetros subyacentes.

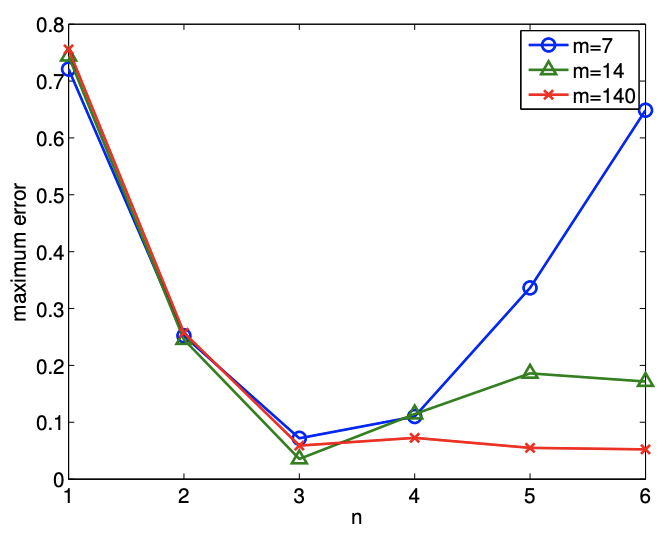
Primero, cuantificamos la calidad de predicción utilizando la diferencia máxima en el modelo y los datos subyacentes limpios,\[e_{\max } \equiv \max _{x \in[-1 / 4,3+1 / 4]}\left|Y_{\text {model }, n}(x ; \hat{\beta})-Y_{\text {clean }}(x)\right| .\] Figura 19.11 (a) muestra la variación en el error máximo de predicción con\(n\) para unos pocos valores diferentes de\(m\). Vemos que obtenemos el ajuste más cercano (en el sentido del error máximo), cuando\(n=3\) - cuando no hay términos “extra” en nuestro modelo. Cuando solo se utilizan puntos de\(m=7\) datos, la calidad de la regresión se degrada significativamente a medida que sobreajustamos los datos\((n>3)\). A medida que la dimensión del modelo\(n\) se acerca al número de mediciones\(m\),, estamos interpolando efectivamente el ruido. La interpolación induce un gran error en las estimaciones de parámetros, y no podemos estimar el ruido ya que estamos ajustando el ruido. Observamos en general que la calidad de la estimación mejora a medida que aumenta el número de muestras.

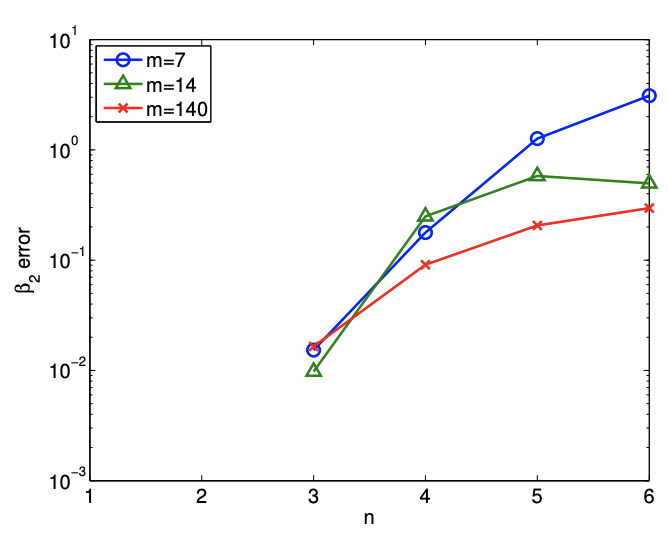
Segundo, cuantificamos la calidad de las estimaciones de parámetros midiendo el error en el coeficiente cuadrático, es decir,\(\left|\beta_{2}-\hat{\beta}_{2}\right|\). La figura 19.11 (b) muestra que, como era de esperar, el error en el

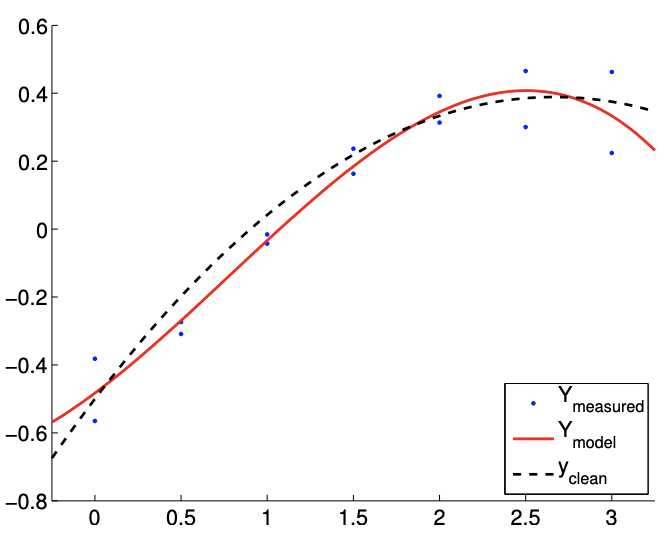
(a)\(m=14\)

b)\(m=140\)

c) intervalos de confianza\(95 \%\) desplazados

d)\(95 \%\) ci in/out (100 realizaciones,\(m=140)\)

Figura 19.10: Ajuste de mínimos cuadrados de una función cuadrática\((c=1)\) utilizando un modelo cúbico.

(a) error máximo de predicción

(b) error en el parámetro\(\beta_{2}\)

c) (normalizado) residual

d) número de condición

Figura 19.11: Variación en la calidad de regresión con sobreajuste.

aumenta el parámetro bajo sobreajuste. En particular, para el pequeño tamaño de muestra de\(m=7\), el error en la estimación para\(\beta_{3}\) aumentos de\(\mathcal{O}\left(10^{-2}\right)\) para\(n=3\) a\(\mathcal{O}(1)\) para\(n \geq 5\). Dado que\(\beta_{3}\) es una\(\mathcal{O}(1)\) cantidad, esto hace que las estimaciones de parámetros sean\(n \geq 5\) esencialmente sin sentido.

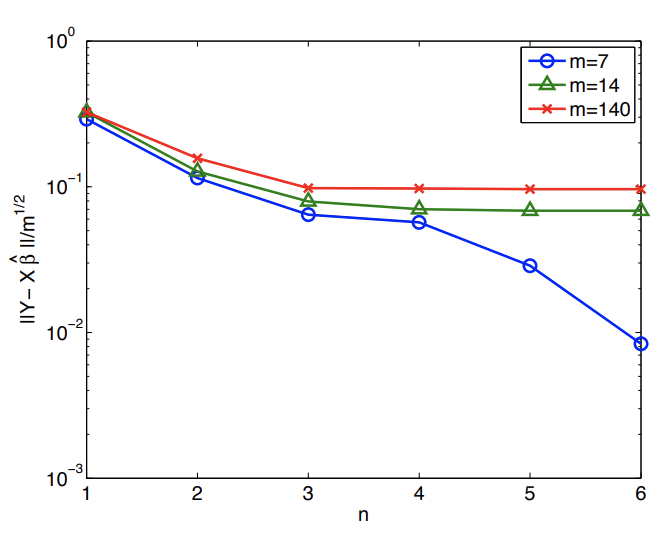
Es importante reconocer que la degradación en la calidad de estimación -ya sea en términos de previsibilidad o error de parámetro- no se debe al mal ajuste en los puntos de datos. En particular, el residual (normalizado),\[\frac{1}{m^{1 / 2}}\|Y-X \hat{\beta}\|,\] que mide el ajuste en los puntos de datos, disminuye a medida que\(n\) aumenta, como se muestra en la Figura 19.11 (c). La disminución del residuo no es sorprendente. Tenemos nuevos coeficientes que anteriormente eran implícitamente cero y por lo tanto los mínimos cuadrados deben proporcionar un residuo que no va en aumento a medida que aumentamos\(n\) y dejamos que estos coeficientes realicen sus valores óptimos (con respecto a la minimización residual). Sin embargo, como vemos en la Figura 19.11 (a) y 19.11 (b), un mejor ajuste en los puntos de datos no implica una mejor representación de la función o parámetros subyacentes.

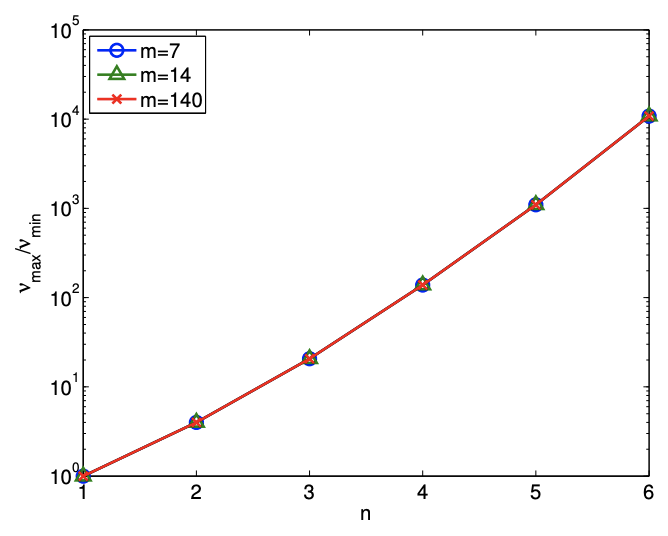
La peor predicción del parámetro se debe al incremento en el condicionamiento del problema\(\left(\nu_{\max } / \nu_{\min }\right)\), como se muestra en la Figura 19.11 (d). Recordemos que el error en el parámetro es una función de ambos residuales (bondad de ajuste en A\(\overline{\text { data points) and conditioning of the problem, i.e. }}\)\[\frac{\|\hat{\beta}-\beta\|}{\|\beta\|} \leq \frac{\nu_{\max }}{\nu_{\min }} \frac{\|X \hat{\beta}-Y\|}{\|Y\|} .\] medida que aumentamos\(n\) para un fijo\(m\), sí reducimos el residual. Sin embargo, claramente el error es mayor tanto en términos de predicción de salida como estimación de parámetros. Una vez más vemos que las estadísticas residuales -y similares de bondad de ajuste comúnmente utilizadas como son\(R^{2}\) - no es la “respuesta final” en términos del éxito de cualquier ejercicio de regresión en particular.

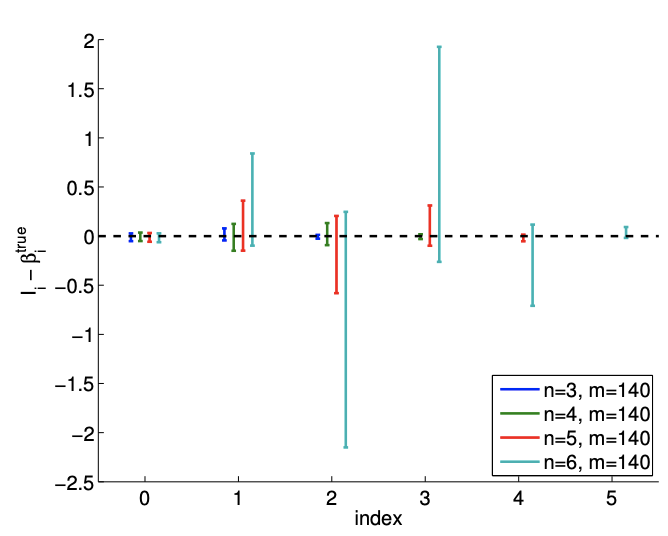
Afortunadamente, similar al ejemplo anterior, esta pobre estimación de los parámetros se refleja en grandes intervalos de confianza, como se muestra en la Figura 19.12. Así, si bien las estimaciones pueden ser malas, se nos informa que no debemos tener mucha confianza en nuestra estimación de los parámetros y que necesitamos más puntos de datos para mejorar el ajuste.

Finalmente, observamos que el condicionamiento del problema refleja dónde elegimos realizar nuestras mediciones, nuestra elección del modelo de respuesta y cómo elegimos representar este modelo de respuesta. Por ejemplo, en lo que respecta a este último, una expansión del orden de Legendre (polinomio) ciertamente\(n\) disminuiría\(\nu_{\max } / \nu_{\min }\), aunque con alguna complicación en la forma en que extraemos diversos parámetros de interés.

Ejemplo 19.2.4 subajuste de una función cuadrática

Consideramos datos gobernados por una función cuadrática ruidosa\(\left(n^{\text {true }} \equiv 3\right)\) de la forma\[Y(x) \sim-\frac{1}{2}+\frac{2}{3} x-\frac{1}{8} c x^{2}+\mathcal{N}\left(0, \sigma^{2}\right) .\] Volvemos a suponer que se desconoce la dependencia entrada-salida. El foco de este ejemplo es inapropiado; es decir, el caso en el que el grado de libertad del modelo\(n\) es menor que el de los datos\(n^{\text {true }}\). En particular, consideraremos un modelo afín\((n=2)\),\[Y_{\text {model }, 2}(x ; \beta)=\beta_{0}+\beta_{1} x,\] que está claramente sesgado (a menos que\(c=0\)).

Para el primer caso, consideramos la verdadera distribución subyacente con\(c=1\), lo que resulta en una fuerte dependencia cuadrática de\(Y\) on\(x\). El resultado del ajuste de la función se muestra en la Figura\(19.13\).

(a)\(m=14\)

b)\(m=140\)

Figura 19.12: La variación en los intervalos de confianza para ajustar una función cuadrática usando\((n=6)\) polinomios cuadráticos\((n=3)\)\((n=4)\)\((n=5)\), cúbicos, cuárticos y quinticos. Anote la diferencia en las escalas para los\(m=140\) casos\(m=14\) y.

Obsérvese que el modelo afín es incapaz de representar la dependencia cuadrática incluso en ausencia de ruido. Así, comparando la Figura 19.13 (a) y 19.13 (b), el ajuste no mejora con el número de puntos de muestreo.

La Figura 19.13 (c) muestra intervalos de confianza individuales típicos para el modelo afín\((n=2)\) usando\(m=14\) y puntos de\(m=140\) muestreo. También se proporcionan intervalos de confianza típicos para el modelo\((n=3)\) cuadrático para la comparación. Centrémonos primero en analizar el ajuste del modelo afín\((n=2)\) utilizando puntos\(m=14\) de muestreo. Observamos que esta realización de intervalos de confianza\(I_{0}\) y\(I_{1}\) no incluye los verdaderos parámetros\(\beta_{0}^{\text {true }}\) y\(\beta_{1}^{\text {true }}\), respectivamente. De hecho, la Figura\(19.13(\mathrm{~d})\) muestra que solo 37 de las 100 realizaciones del intervalo de confianza\(I_{0}\) incluyen\(\beta_{0}^{\text {true }}\) y que ninguna de las realizaciones de\(I_{1}\) incluye\(\beta_{1}^{\text {true }}\). Por lo tanto, la frecuencia con la que reside el valor verdadero en el intervalo de confianza es significativamente menor que\(95 \%\). Esto se debe a la presencia del error de sesgo, que viola nuestras suposiciones sobre el comportamiento del ruido, las suposiciones en las que se basa nuestra estimación del intervalo de confianza. De hecho, a medida que aumentamos el número de puntos de muestreo de\(m=14\) a\(m=140\) vemos que los intervalos de confianza para ambos\(\beta_{0}\) y se\(\beta_{1}\) aprietan; sin embargo, convergen hacia valores incorrectos. Así, ante la presencia de sesgo, los intervalos de confianza no son confiables, y su convergencia implica poco sobre la calidad de las estimaciones.

Consideremos ahora el segundo caso con\(c=1 / 10\). Este caso resulta en una dependencia cuadrática mucho más débil de\(Y\) on\(x\). Los ajustes típicos obtenidos utilizando el modelo afín se muestran en la Figura 19.14 (a) y 19.14 (b) para\(m=14\) y puntos de\(m=140\) muestreo, respectivamente. Tenga en cuenta que el ajuste es mejor que el\(c=1\) caso porque los\(c=1 / 10\) datos se pueden representar mejor usando el modelo afín.

Los intervalos de confianza típicos, mostrados en la Figura 19.14 (c), confirman que los intervalos de confianza son más confiables que en el\(c=1\) caso. De las 100 realizaciones para el\(m=14\) caso,\(87 \%\) y\(67 \%\) de los intervalos de confianza incluyen los valores verdaderos\(\beta_{0}^{\text {true }}\) y\(\beta_{1}^{\text {true }}\), respectivamente. Las frecuencias son menores que las\(95 \%\), es decir, los intervalos de confianza no son tan confiables como su pretensión, debido a la presencia de sesgo. Sin embargo, son más confiables que el caso con una dependencia cuadrática más fuerte, es decir, un sesgo más fuerte. Recordemos que un sesgo menor que conduce a un error menor es consistente con los límites de error deterministas que desarrollamos en presencia de sesgo.

Similar al\(c=1\) caso, el intervalo de confianza se estrecha con el número de muestras\(m\), pero

(a)\(m=14\)

b)\(m=140\)

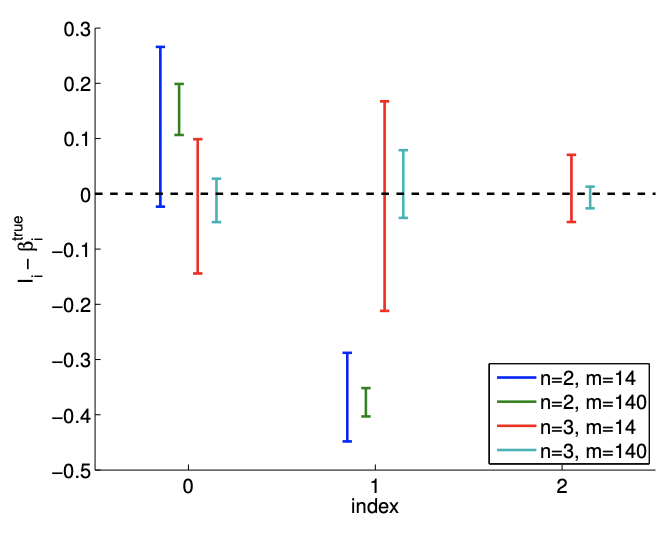
c) intervalos de confianza\(95 \%\) desplazados

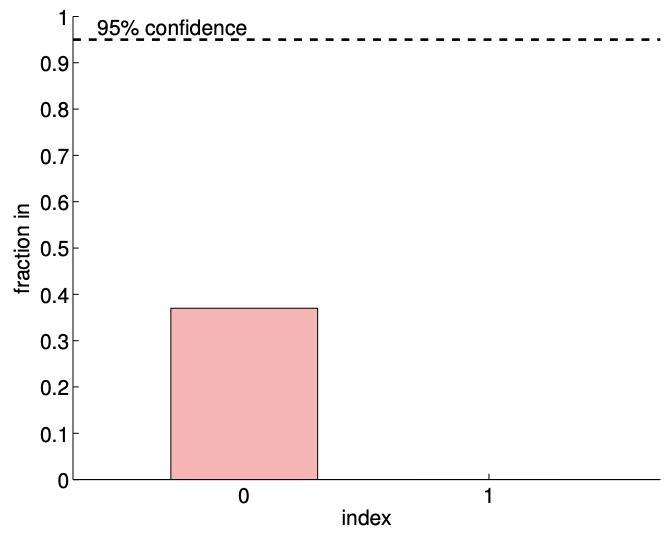
d)\(95 \% \mathrm{ci} \mathrm{in/out}(100\) las realizaciones,\(m=14)\)

Figura 19.13: Ajuste de mínimos cuadrados de una función cuadrática\((c=1)\) utilizando un modelo afín.

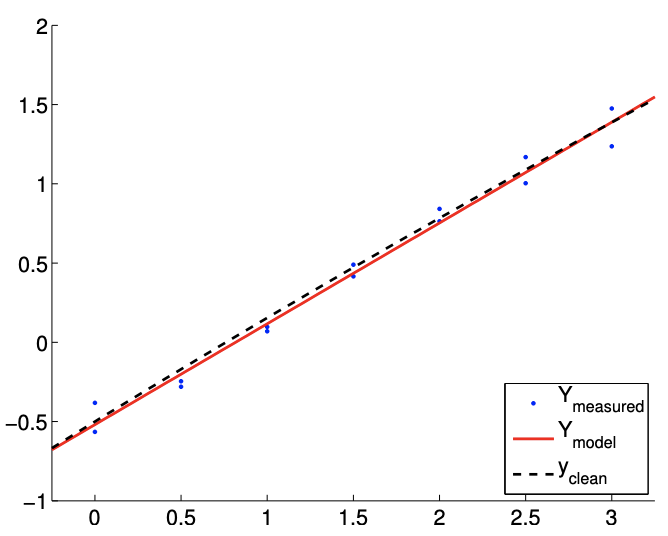
(a)\(m=14\)

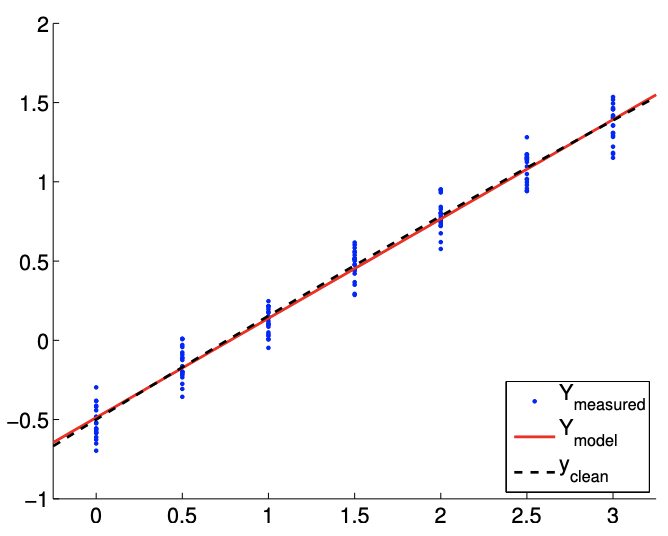
b)\(m=140\)

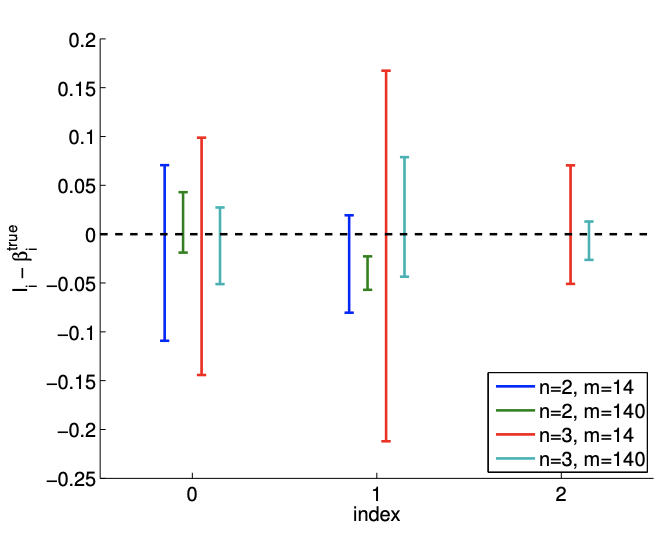
c) intervalos de confianza\(95 \%\) desplazados

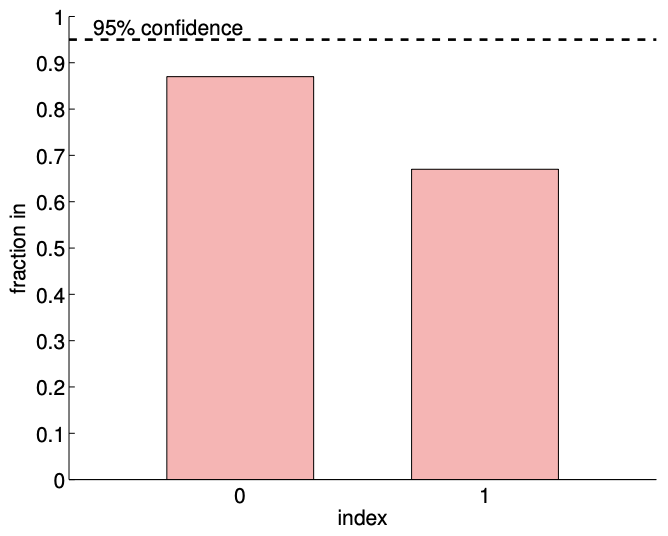
d)\(95 \% \mathrm{ci} \mathrm{in} /\) fuera (100 realizaciones,\(m=14)\)

Figura 19.14: Ajuste de mínimos cuadrados de una función cuadrática\((c=1 / 10)\) utilizando un modelo afín.

convergen a un valor equivocado. En consecuencia, la confiabilidad de los intervalos de confianza disminuye con\(m\).

Material Avanzado