21.1: ODEs lineales escalares de primer orden

Problema con el modelo

Consideremos un problema canónico de valor inicial (IVP),

\ begin {alineado}
\ frac {d u} {d t} &=\ lambda u+f (t),\ quad 0<t<t_ {f}\\
u (0) &=u_ {0}
\ end {alineado}

El objetivo es encontrar\(u\) sobre todo el tiempo\(t ∈ [0, t_f]\) que satisfaga la ecuación diferencial ordinaria (ODE) y la condición inicial. Este problema pertenece a la clase de problemas de valor inicial (IVP) ya que complementamos la ecuación con condición (s) solo en el momento inicial. La ODE es de primer orden porque la derivada más alta que aparece en la ecuación es la derivada de primer orden; debido a que es de primer orden, solo se requiere una condición inicial para definir una solución única. La ODE es lineal porque la expresión es lineal con respecto a\(u\) y su derivada\(du/dt\); tenga en cuenta que\(f\) no tiene que ser una función lineal de\(t\) para que la ODE sea lineal. Por último, la ecuación es escalar ya que sólo tenemos una sola desconocida,\(u(t) ∈ \mathbb{R}\). El coeficiente\(λ ∈ \mathbb{R}\) controla el comportamiento de la ODE;\(λ < 0\) resulta en un comportamiento estable (es decir, en descomposición), mientras que\(λ > 0\) resulta en un comportamiento inestable (es decir, en crecimiento).

Podemos motivar este problema de modelo (con\(λ < 0\)) físicamente con una simple situación de transferencia de calor. Consideramos un cuerpo a temperatura inicial\(u_0 > 0\) que luego es “sumergido” o “sumergido” en un flujo de fluido —convección forzada o natural— de temperatura ambiente (lejos del cuerpo) cero. (Más físicamente, podemos ver u0 como la elevación de temperatura por encima de alguna temperatura ambiente distinta de cero.) Modelamos la transferencia de calor del cuerpo al fluido mediante un coeficiente de transferencia de calor,\(h\). También permitimos la generación de calor dentro del cuerpo\(q(t)\), debido (digamos) al calentamiento Joule o radiación. Si ahora asumimos que el número Biot —el producto de h y el “diámetro” del cuerpo en el numerador, la conductividad térmica del cuerpo en el denominador— es pequeño, la temperatura del cuerpo será más o menos uniforme en el espacio. En este caso, la temperatura del cuerpo en función del tiempo,\(u(t)\), se regirá por nuestra ecuación diferencial ordinaria (ODE) problema de valor inicial (IVP), con\(λ = −h \text{Area}/ρc\) Vol y\(f(t) = q(t)/ρc\) Vol, donde\(ρ\) y\(c\) son la densidad corporal y el calor específico, respectivamente, y Área y Vol son la superficie corporal y el volumen, respectivamente.

De hecho, es posible expresar la solución a nuestro problema modelo en forma cerrada (como una convolución). Nuestro interés en el problema del modelo no se debe, pues, a que requerimos un procedimiento de solución numérica para este problema simple en particular. Más bien, como veremos, nuestro problema modelo proporcionará una base sobre la cual construir y comprender procedimientos numéricos para problemas mucho más difíciles —que no admiten una solución de forma cerrada.

Solución Analítica

Antes de perseguir métodos numéricos para resolver el IVP, estudiemos la solución analítica para algunos casos que proporcionan una visión de la solución y también sugieren casos de prueba para nuestros enfoques numéricos.

Ecuación Homogénea

El primer caso considerado es el caso homogéneo, es decir,\(f(t) = 0\). Sin pérdida de generalidad, pongámonos\(u_0 = 1\). Por lo tanto, consideramos

\ begin {alineado}
\ frac {d u} {d t} &=\ lambda u,\ quad 0<t<t_ {f}\\
u (0) &=1
\ end {alineado}

Encontramos la solución analítica siguiendo el procedimiento estándar para obtener la solución homogénea, es decir, sustituta\(u = \alpha e^{\beta t\) para obtener

\ begin {alineado}
(\ mathrm {LHS}) &=\ frac {d u} {d t} =\ frac {d} {d t}\ izquierda (\ alpha e^ {\ beta t}\ derecha) =\ alfa\ beta e^ {t}\\
(\ mathrm {RHS}) &=\ lambda\ alfa e^ {\ beta t}
\ end {alineado}

Equiparando el LHS y el RHS, obtenemos\(β = λ\). La solución es de la forma\(u(t) = \alpha e^{λt}\). El coeficiente\(\alpha\) es especificado por la condición inicial, i.e.

\(u(t = 0) = \alpha = 1\);

así, el coeficiente es\(\alpha = 1\). La solución a la ODE homogénea es

\(u(t) = e^{λt} \).

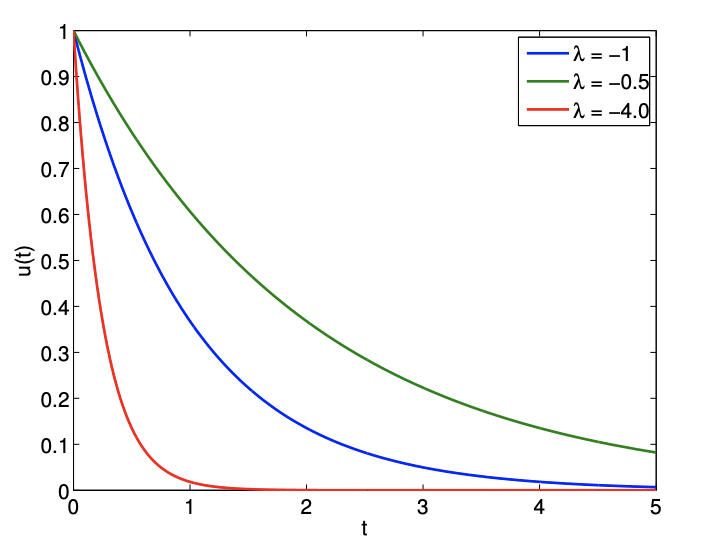
Tenga en cuenta que la solución comienza desde 1 (por la condición inicial) y decae a cero para\(λ < 0\). La tasa de decaimiento está controlada por la constante de tiempo\(1/|λ|\): cuanto mayor es la\(λ\), más rápida es la descomposición. La solución para algunos valores diferentes de se\(λ\) muestran en la Figura 21.1. Observamos que para\(λ > 0\) la solución crece exponencialmente en el tiempo: el sistema es inestable. (De hecho, en la mayoría de las situaciones físicas, en algún momento términos adicionales —por ejemplo, los efectos no lineales no incluidos en nuestro modelo simple— se volverían importantes y asegurarían la saturación en algún estado estacionario.) En lo que resta de este capítulo a menos que específicamente se indique lo contrario asumiremos que\(λ < 0\).

Forzando Constante

A continuación, consideramos un caso de forzamiento constante con\(u_0 = 0\) y\(f(t) = 1\), i.e.

\ begin {alineado}
\ frac {d u} {d t} &=\ lambda u + 1,\\
u (0) &=0.
\ end {alineado}

Figura 21.1: Soluciones a la ecuación homogénea.

Ya encontramos la solución homogénea a la ODE. Ahora encontramos la solución particular. Debido a que el término forzoso es constante, consideramos una solución particular de la forma\(u_p(t) = \gamma\). Sustitución de\(u_p\) rendimientos

\(0=\lambda \gamma+1 \quad \Rightarrow \quad \gamma=-\frac{1}{\lambda}\)

Así, nuestra solución es de la forma

\(u(t) = − \frac{1} {λ} + \alpha e^{λt}\).

El cumplimiento de la condición inicial,

\(u(t=0)=-\frac{1}{\lambda}+\alpha=0 \quad \Rightarrow \quad \alpha=\frac{1}{\lambda}\)

Así, nuestra solución viene dada por

\(u(t) = \frac{1} {λ} (e^{λt} − 1) \).

Las soluciones para algunos valores diferentes de se\(λ\) muestran en la Figura 21.2. Porque\(λ < 0\), después del transitorio que decae en la escala de tiempo\(1/|λ|\), la solución se asienta al valor de estado estacionario de\(−1/λ\).

Forzado sinusoidal

Consideremos un caso final con\(u_0 = 0\) y un forzamiento sinusoidal\(f(t) = cos(ωt)\), i.e.

\ begin {alineado}
\ frac {d u} {d t} &=\ lambda u+\ cos (\ omega t)\\
u_ {0} &=0
\ end {alineado}

Debido a que el término forzoso es sinusoidal con la frecuencia\(ω\), la solución particular es de la forma\(u_p(t) = \gamma sin(ωt) + δ cos(ωt)\). Sustitución de la solución particular por los rendimientos de ODE

\ begin {alineado}
(\ mathrm {LHS}) &=\ frac {d u_ {p}} {d t} =\ omega (\ gamma\ cos (\ omega t) -\ delta\ sin (\ omega t))\\
(\ mathrm {RHS}) &=\ lambda (\ gamma\ sin (\ omega t) +\ delta\ cos (\ omega t)) +\ cos (\ omega t)
\ final {alineado}

Figura 21.2: Soluciones a la ODE con forzamiento constante unitario.

Equiparando el LHS y el RHS y recogiendo coeficientes similares obtenemos

\(ω \gamma = λδ + 1 \),

\(−ωδ = λ\gamma\).

La solución a este sistema lineal viene dada por\(\gamma = ω/(ω^2 + λ^2 )\) y\(δ = −λ/(ω^2 + λ^2 )\). Así, la solución es de la forma

\(u(t)=\frac{\omega}{\omega^{2}+\lambda^{2}} \sin (\omega t)-\frac{\lambda}{\omega^{2}+\lambda^{2}} \cos (\omega t)+\alpha e^{\lambda t}\)

Imponiendo la condición límite, obtenemos

\(u(t=0)=-\frac{\lambda}{\omega^{2}+\lambda^{2}}+\alpha=0 \quad \Rightarrow \quad \alpha=\frac{\lambda}{\omega^{2}+\lambda^{2}} .\)

Así, la solución al IVP con el forzamiento sinusoidal es

\(u(t)=\frac{\omega}{\omega^{2}+\lambda^{2}} \sin (\omega t)-\frac{\lambda}{\omega^{2}+\lambda^{2}}\left(\cos (\omega t)-e^{\lambda t}\right)\)

Observamos que para baja frecuencia no hay desplazamiento de fase; sin embargo, para alta frecuencia hay un desplazamiento de\(\pi/2\) fase.

Las soluciones para\(λ = −1, ω = 1\) y\(λ = −20, ω = 1\) se muestran en la Figura 21.3. El comportamiento de estado estacionario es controlado por la función de forzamiento sinusoidal y tiene la escala de tiempo de\(1/ω\). Por otro lado, el transitorio inicial está controlado por\(λ\) y tiene la escala de tiempo de\(1/|λ|\). En particular, tenga en cuenta que para\(|λ|>> ω\), la solución exhibe escalas de tiempo muy diferentes en el estado transitorio y en el estado estacionario (periódico). Este es un ejemplo de una ecuación rígida (veremos otro ejemplo al concluir esta unidad). Resolver una ecuación rígida introduce desafíos computacionales adicionales para esquemas numéricos, como veremos en breve.

Primer método numérico: Euler hacia atrás (implícito)

En esta sección, consideramos al integrador de Euler hacia atrás para resolver problemas de valor inicial. Primero introducimos el esquema de paso de tiempo y luego discutimos una serie de propiedades que caracterizan el esquema.

Figura 21.3: Soluciones a la ODE con forzamiento sinusoidal.

Discretización

Para resolver un IVP numéricamente, primero discretizamos el dominio del tiempo\(]0, t_f ]\) en\(J\) segmentos. Los puntos de tiempo discretos vienen dados por

\(t^{j}=j \Delta t, \quad j=0,1, \ldots, J=t_{f} / \Delta t\)

donde\(∆t\) esta el paso del tiempo. Por simplicidad, asumimos en este capítulo que el paso del tiempo es constante a lo largo de la integración del tiempo.

El método Atrás de Euler se obtiene aplicando la Fórmula de Diferencia Atrás de primer orden (ver Unidad I) a la derivada de tiempo. A saber, aproximamos la derivada del tiempo por

\(\dfrac{du}{dt} \approx \dfrac{\tilde{u}^j - \tilde{u}{j-1}}{\Delta t}\),

donde\(\tilde{u}^j = \tilde{u}(t^j )\) esta la aproximacion a\(u(t^j )\) y\(∆t = t^j − t^{j−1}\) es el paso de tiempo. Sustituyendo la aproximación en la ecuación diferencial, obtenemos una ecuación de diferencia

\(\dfrac{\tilde{u}^j - \tilde{u}^{j-1}}{\Delta t} = \lambda \tilde{u}^j + f(t^j), \quad j = 1,....,J\),

\(\tilde{u}^0 = u_0\),

para\(\tilde{u}^j, j = 0, . . . , J.\) Nota el esquema se llama “implícito” porque el nivel de tiempo\(j\) aparece en el lado derecho. Podemos pensar en Euler Hacia atrás como una especie de rectángulo, regla de integración correcta —pero ahora el integrando no se conoce a priori.

Anticipamos que la solución\(\tilde{u}^j, j = 1, . . . , J,\) se acerca a la solución verdadera\(u(t^j ), j = 1, . . . , J\), ya que el paso de tiempo se hace más pequeño y la aproximación de diferencia finita se acerca al sistema continuo. Para que se produzca esta convergencia a la verdadera solución, la discretización debe poseer dos propiedades importantes: consistencia y estabilidad. Observe que nuestro análisis aquí es más sutil que el análisis en la Unidad I. En la Unidad I observamos el error en la aproximación de diferencias finitas; aquí, nos interesa el error inducido por la aproximación de diferencias finitas sobre la solución aproximada de la ODE IVP.

Consistencia

La consistencia es una propiedad de una discretización que asegura que la ecuación discreta se aproxime al mismo proceso que la ODE subyacente a medida que el paso de tiempo va a cero. Esta es una propiedad importante, porque si el esquema no es consistente con la ODE, entonces el esquema está modelando un proceso diferente y la solución no convergería a la verdadera solución.

Definamos más formalmente la noción de consistencia. Primero definimos el error de truncamiento sustituyendo la verdadera solución\(u(t)\) en la discretización hacia atrás de Euler, i.e.

\(τ_{\text{truc}}^j ≡ \dfrac{u(t^j) - u(t^{j-1})}{\Delta t} - \lambda u (t^j) - f(t^j), \quad j = 1,...,J\).

Tenga en cuenta que el error de truncamiento\(τ^j_{\text{trunc}}\),, mide la medida en que la solución exacta a la ODE no satisface la ecuación de diferencia. En general, la solución exacta no satisface la ecuación de diferencia, entonces\(τ^j_{\text{trunc}} \neq 0\). De hecho, como veremos en breve, si\(τ^j_{\text{trunc}} = 0, j = 1, . . . , J\), entonces\(\tilde{u}^j = u(t^j ),\) es decir,\(\tilde{u}^j\) es la solución exacta a la ODE en los puntos de tiempo.

Estamos particularmente interesados en el mayor de los errores de truncamiento, que es en cierto sentido la mayor discrepancia entre la ecuación diferencial y la ecuación de diferencia. Denotamos esto usando la norma del infinito,

\(\left\|\tau_{\text {trunc }}\right\|_{\infty}=\max _{j=1, \ldots, J}\left|\tau_{\text {trunc }}^{j}\right|\)

Un esquema es consistente con la ODE si

\(\left\|\tau_{\text {trunc }}\right\|_{\infty} \rightarrow 0 \quad \text { as } \quad \Delta t \rightarrow 0 \).

La ecuación de diferencia para un esquema consistente se acerca a la ecuación diferencial como\(\Delta t \rightarrow\) 0. Sin embargo, esto no implica necesariamente que la solución a la ecuación de diferencia,\(\tilde{u}\left(t^{j}\right)\), se acerque a la solución a la ecuación diferencial,\(u\left(t^{j}\right)\).

El esquema de Euler Atrás es consistente. En particular

\(\left\|\tau_{\text {trunc }}\right\|_{\infty} \leq \frac{\Delta t}{2} \max _{t \in\left[0, t_{f}\right]}\left|\frac{d^{2} u}{d t^{2}}(t)\right| \rightarrow 0 \quad \text { as } \quad \Delta t \rightarrow 0 .\)

A continuación demostramos este resultado.

Comenzar material avanzado

Analicemos ahora la consistencia del esquema de integración hacia atrás de Euler. Primero aplicamos la expansión de Taylor a\(u\left(t^{j-1}\right)\) aproximadamente\(t^{j}\), es decir.

\(u\left(t^{j-1}\right)=u\left(t^{j}\right)-\Delta t \frac{d u}{d t}\left(t^{j}\right)-\underbrace{\int_{t^{j-1}}^{t^{j}}\left(\int_{t^{j-1}}^{\tau} \frac{d^{2} u}{d t^{2}}(\gamma) d \gamma\right) d \tau}_{s^{j}(u)} .\)

Este resultado es sencillo de derivar. Por el teorema fundamental del cálculo,

\(\int_{t^{j-1}}^{\tau} \frac{d u^{2}}{d t^{2}}(\gamma) d \gamma=\frac{d u}{d t}(\tau)-\frac{d u}{d t}\left(t^{j-1}\right) .\)

Integrando ambos lados sobre\(] t^{j-1}, t^{j}[\),

\ begin {alineado}
\ int_ {t^ {j-1}} ^ {t^ {j}}\ izquierda (\ int_ {t^ {j-1}} ^ {\ tau}\ frac {d u^ {2}} {d t^ {2}} (\ gamma) d\ gamma\ derecha) d\ tau &=\ int_ {t^ {j-1}} ^ {t^ j {}}\ izquierda (\ frac {d u} {d t} (\ tau)\ derecha) d\ tau-\ int_ {t^ {j-1}} ^ {t^ {j}}\ izquierda (\ frac {d u} {d t}\ izquierda (t^ {j-1}\ derecha)\ derecha) d\ tau\
&=u\ izquierda (t^ {j}\ derecha) -u\ izquierda (t^ {j-1}\ derecha) -\ izquierda (t^ {j} -t^ {j-1}\ derecha)\ frac {d u} {d t}\ izquierda (t^ {j-1}\ derecha)\\
&=u\ izquierda (t^ {j}\ derecha) -u\ izquierda (t^ {j-1} derecha\) -\ Delta t\ frac {d u} {d t}\ izquierda (t^ {j-1}\ derecha)
\ final {alineado}

Sustitución de la expresión al lado derecho de los rendimientos de expansión de la serie Taylor

\(u\left(t^{j}\right)-\Delta t \frac{d u}{d t}\left(t^{j}\right)-s^{j}(u)=u\left(t^{j}\right)-\Delta t \frac{d u}{d t}\left(t^{j}\right)-u\left(t^{j}\right)+u\left(t^{j-1}\right)+\Delta t \frac{d u}{d t}\left(t^{j-1}\right)=u\left(t^{j-1}\right),\)

lo que demuestra el resultado deseado.
Sustituyendo la expansión de Taylor en la expresión por el error de truncamiento,

\ begin {alineado}
\ tau_ {\ text {trunc}} ^ {j} &=\ frac {u\ izquierda (t^ {j}\ derecha) -u\ izquierda (t^ {j-1}\ derecha)} {\ Delta t} -\ lambda u\ izquierda (t^ {j}\ derecha) -f\ izquierda (t^ {j}\ derecha)\\
&=\ frac {1} {\ Delta t}\ izquierda (u\ izquierda (t^ {j}\ derecha) -\ izquierda (u\ izquierda (t^ {j}\ derecha) -\ Delta t\ frac {d u} {d t}\ izquierda (t^ {j}\ derecha) -s^ {j} (u )\ derecha)\ derecha) -\ lambda u\ izquierda (t^ {j}\ derecha) -f\ izquierda (t^ {j}\ derecha)\\
&=\ underbrackets {\ frac {d u} {d t}\ izquierda (t^ {j}\ derecha) -\ lambda u\ izquierda (t^ {j}\ derecha) -f\ izquierda (t^ {j}\ derecha)} _ {=0:\ text {por ODE}} +\ frac {s^ {j} (u)} {\ Delta t}\\
&=\ frac {s^ {j} (u)} {\ Delta t}.
\ end {alineado}

Ahora vinculamos el término\(s^{j}(u)\) restante en función de\(\Delta t\). Tenga en cuenta que

\ begin {alineado}
s^ {j} (u) &=\ int_ {t^ {j-1}} ^ {t^ {j}}\ left (\ int_ {t^ {j-1}} ^ {\ tau}\ frac {d^ {2} u} {d t^ {2}} (\ gamma) d\ gamma\ derecha) d\ tau\ leq\ int_ {t^ {j-1}} ^ {t^ {j}}\ izquierda (\ int_ {t^ {j-1}} ^ {\ tau}\ izquierda|\ frac {d^ {2} u} {d t^ {2}} (\ gamma)\ derecha| d\ gamma\ derecha) d\ tau\\
&\ leq\ max _ {t\ in \ izquierda [t^ {j-1}, t^ {j}\ derecha]}\ izquierda|\ frac {d^ {2} u} {d t^ {2}} (t)\ derecha|\ int_ {t^ {j-1}} ^ {t^ {j}}\ int_ {t^ {j-1}} ^ {\ tau} d\ gamma d\ tau\\
&= max _ {t\ in\ izquierda [t^ {j-1}, t^ {j}\ derecha]}\ izquierda|\ frac {d^ {2} u} {d t^ {2}} (t)\ derecha|\ frac {\ Delta t^ {2}} {2},\ quad j=1,\ ldots, J.
\ end {alineado}

Entonces, el error máximo de truncamiento es

\(\left\|\tau_{\text {trunc }}\right\|_{\infty}=\max _{j=1, \ldots, J}\left|\tau_{\text {trunc }}^{j}\right| \leq \max _{j=1, \ldots, J}\left(\frac{1}{\Delta t} \max _{t \in\left[t^{-1}, t, t^{j}\right]}\left|\frac{d^{2} u}{d t^{2}}(t)\right| \frac{\Delta t^{2}}{2}\right) \leq \frac{\Delta t}{2} \max _{t \in\left[0, t_{f}\right]}\left|\frac{d^{2} u}{d t^{2}}(t)\right|\)

Vemos que

\(\left\|\tau_{\text {trunc }}\right\|_{\infty} \leq \frac{\Delta t}{2} \max _{t \in\left[0, t_{f}\right]}\left|\frac{d^{2} u}{d t^{2}}(t)\right| \rightarrow 0 \quad \text { as } \quad \Delta t \rightarrow 0\)

Así, el esquema de Euler Atrás es consistente.

Material Avanzado

Estabilidad

La estabilidad es una propiedad de una discretización que asegura que el error en la aproximación numérica no crezca con el tiempo. Esta es una propiedad importante, ya que asegura que un pequeño error de truncamiento introducido en cada paso de tiempo no cause una divergencia catastrófica en la solución a lo largo del tiempo.

Para estudiar la estabilidad, consideremos un IVP homogéneo,

\(\dfrac{du}{dt} = \lambda u\),

\(u(0) = 1\).

Recordemos que la verdadera solución es de la forma\(u(t) = e^{λt}\) y decae para\(λ < 0\). Aplicando el esquema Atrás de Euler, obtenemos

\ begin {alineado}
\ frac {\ tilde {u} ^ {j} -\ tilde {u} ^ {j-1}} {\ Delta t} &=\ lambda\ tilde {u} ^ {j},\ quad j=1,\ ldots, J,\\
u^ {0} &=1.
\ end {alineado}

Se dice que un esquema es absolutamente estable si

\(\left|\tilde{u}^{j}\right| \leq\left|\tilde{u}^{j-1}\right|, \quad j=1, \ldots, J .\)

Alternativamente, podemos definir el factor de amplificación\(\gamma\), como

\(\gamma \equiv \frac{\left|\tilde{u}^{j}\right|}{\left|\tilde{u}^{j-1}\right|} .\)

La estabilidad absoluta lo requiere\(\gamma \leq 1\) para todos\(j=1, \ldots, J\).

Demostremos ahora que el esquema de Euler Hacia atrás es estable para todos\(\Delta t\) (para\(\lambda<0\)). Reordenando la ecuación de diferencia,

\ begin {alineado}
\ tilde {u} ^ {j} -\ tilde {u} ^ {j-1} &=\ lambda\ Delta t\ tilde {u} ^ {j}\
\ tilde {u} ^ {j} (1-\ lambda\ Delta t) &=\ tilde {u} ^ {j-1}\\\ izquierda|
\ tilde {u} ^ {j}\ derecha||1-\ lambda\ Delta t| &=\ izquierda|\ tilde {u} ^ {j-1}\ derecha|.
\ end {alineado}

Entonces, tenemos

\(\gamma=\frac{\left|\tilde{u}^{j}\right|}{\left|\tilde{u}^{j-1}\right|}=\frac{1}{|1-\lambda \Delta t|} .\)

Recordando que\(\lambda<0\) (y\(\Delta t>0\)), tenemos

\(\gamma=\frac{1}{1-\lambda \Delta t}<1 .\)

Así, el esquema de Euler hacia atrás es estable para todos los $\ Delta t$ para el problema del modelo considerado. Se dice que el esquema es incondicionalmente estable porque es estable para todos\(\Delta t\). Algunos esquemas solo son condicionalmente estables, lo que significa que el esquema es estable para\(\Delta t \leq \Delta t_{\mathrm{cr}}\), donde\(\Delta t_{\text {cr }}\) hay algún paso de tiempo crítico.

Convergencia: Teorema de Equivalencia Dahlquist

Ahora definimos la noción de convergencia. Un esquema es convergente si la aproximación numérica se acerca a la solución analítica a medida que se reduce el paso de tiempo. Formalmente, esto significa que

\(\tilde{u}^{j} \equiv \tilde{u}\left(t^{j}\right) \rightarrow u\left(t^{j}\right) \quad\)para fijo\(t^{j}\) como\(\Delta t \rightarrow 0\)

Tenga en cuenta que tiempo fijo\(t^{j}\) significa que el índice de tiempo debe ir al infinito (es decir, se requiere un número infinito de pasos de tiempo) como\(\Delta t \rightarrow 0\) porque\(t^{j}=j \Delta t\). Así, la convergencia requiere que no se acumule demasiado error en cada paso de tiempo. Además, el error generado en un paso dado no debería crecer con el tiempo.

La relación entre consistencia, estabilidad y convergencia se resume en el teorema de equivalencia de Dahlquist. El teorema establece que la consistencia y la estabilidad son la condición necesaria y suficiente para un esquema convergente, i.e.

consistencia\(+\) estabilidad\(\Leftrightarrow\) convergencia

Por lo tanto, sólo necesitamos demostrar que un esquema es consistente y (absolutamente) estable para demostrar que el esquema es convergente. En particular, el esquema de Euler Hacia atrás es convergente porque es consistente y (absolutamente) estable.

Comenzar material avanzado

Ejemplo 21.1.1 Consistencia, estabilidad y convergencia para Euler hacia atrás

En este ejemplo, estudiaremos en detalle la relación entre consistencia, estabilidad y convergencia para el esquema de Euler Atrás. Denotemos el error en la solución por\(e^{j}\),

\(e^{j} \equiv u\left(t^{j}\right)-\tilde{u}\left(t^{j}\right)\)

Primero relacionamos la evolución del error con el error de truncamiento. Para comenzar, recordamos que

\ begin {aligned}
&u\ left (t^ {j}\ right) -u\ left (t^ {j-1}\ right) -\ lambda\ Delta t u\ left (t^ {j}\ right) -\ Delta t f\ left (t^ {j}\ right) =\ Delta t\ tau_ {\ text {trunc}} ^ {j}\\
& tilde {u}\ izquierda (t^ {j}\ derecha) -\ tilde {u}\ izquierda (t^ {j-1}\ derecha) -\ lambda\ Delta t\ tilde {u}\ izquierda (t^ {j}\ derecha) -\ Delta t f\ izquierda (t^ {j}\ derecha) =0
\ final {alineado}

restando estas dos ecuaciones y usando la definición del error obtenemos

\(e^{j}-e^{j-1}-\lambda \Delta t e^{j}=\Delta t \tau_{\text {trunc }}^{j}\)

o, reordenando la ecuación,

\((1-\lambda \Delta t) e^{j}-e^{j-1}=\Delta t \tau_{\text {trunc }}^{j}\).

Vemos que el error en sí satisface la ecuación de diferencia hacia atrás de Euler con el error de truncamiento como término fuente. Claramente, si el error de truncamiento\(τ^j_{\text{trunc}}\) es cero para todos los pasos de tiempo (y el error inicial es cero), entonces el error permanece cero. En otras palabras, si el error de truncamiento es cero entonces el esquema produce la solución exacta en cada paso de tiempo.

Sin embargo, en general, el error de truncamiento es distinto de cero, y nos gustaría analizar su influencia en el error. Multipliquemos la ecuación por\((1 − λ∆t)^{j−1}\) para obtener

\((1-\lambda \Delta t)^{j} e^{j}-(1-\lambda \Delta t)^{j-1} e^{j-1}=(1-\lambda \Delta t)^{j-1} \Delta t \tau_{\text {trunc }}^{j}\)

Ahora, calculemos la suma para\(j=1, \ldots, n\), para algunos\(n \leq J\)

\(\sum_{j=1}^{n}\left[(1-\lambda \Delta t)^{j} e^{j}-(1-\lambda \Delta t)^{j-1} e^{j-1}\right]=\sum_{j=1}^{n}\left[(1-\lambda \Delta t)^{j-1} \Delta t \tau_{\text {trunc }}^{j}\right]\)

Se trata de una serie telescópica y todos los términos medios en el lado izquierdo cancelan. De manera más explícita,

\ begin {alineado}
(1-\ lambda\ Delta t) ^ {n} e^ {n} - (1-\ lambda\ Delta t) ^ {n-1} e^ {n-1} & =( 1-\ lambda\ Delta t) ^ {n-1}\ Delta t\ tau_ {\ texto {trunc}} ^ {n}\\
(1-\ lambda\ Delta t) ^ {n-1} e^ {n-1} - (1-\ lambda\ Delta t) ^ {n-2} e^ {n-2} & =( 1-\ lambda\ Delta t) ^ {n-2}\ Delta t\ tau_ {\ texto {trunc }} ^ {n-1}\\
&\ vdots\\
(1-\ lambda\ Delta t) ^ {2} e^ {2} - (1-\ lambda\ Delta t) ^ {1} e^ {1} & =( 1-\ lambda\ Delta t) ^ {1}\ Delta t\ tau_ {\ text {trunc}} ^ {2}\\
(1-\ lambda Delta\ t) ^ {1} e^ {1} - (1-\ lambda\ Delta t) ^ {0} e^ {0} & =( 1-\ lambda\ Delta t) ^ {0}\ Delta t\ tau_ {\ texto {trunc}} ^ {1}
\ end {alineado}

simplifica a

\((1-\lambda \Delta t)^{n} e^{n}-e^{0}=\sum_{j=1}^{n}(1-\lambda \Delta t)^{j-1} \Delta t \tau_{\text {trunc }}^{j}\)

Recordemos que establecemos\(\tilde{u}^{0}=\tilde{u}\left(t^{0}\right)=u\left(t^{0}\right)\), por lo que el error inicial es cero\(\left(e^{0}=0\right)\). Así, nos quedamos con

\((1-\lambda \Delta t)^{n} e^{n}=\sum_{j=1}^{n}(1-\lambda \Delta t)^{j-1} \Delta t \tau_{\text {trunc }}^{j}\)

o, equivalentemente,

\(e^{n}=\sum_{j=1}^{n}(1-\lambda \Delta t)^{j-n-1} \Delta t \tau_{\text {trunc }}^{j}\)

Recordando eso\(\left\|\tau_{\text {trunc }}\right\|_{\infty}=\max _{j=1, \ldots, J}\left|\tau_{\text {trunc }}^{j}\right|\), podemos encuadernar el error por

\(\left|e^{n}\right| \leq \Delta t\left\|\tau_{\text {trunc }}\right\|_{\infty} \sum_{j=1}^{n}(1-\lambda \Delta t)^{j-n-1}\)

Recordando el factor de amplificación para el esquema hacia atrás de Euler\(\gamma = 1/(1−λ∆t)\),, la suma se puede reescribir como

\ begin {alineado}
\ sum_ {j = 1} ^ {n} (1-\ lambda\ Delta t) ^ {j-n-1} &=\ frac {1} {(1-\ lambda\ Delta t) ^ {n}} +\ frac {1} {(1-\ lambda\ Delta t) ^ {n-1}} +\ cdots+\ frac {1} {(1-\ Delta t) ^ {n-1} +\ cdots+\ frac {1} {(1-\ Delta t) ^ {lambda\ Delta t)}\\
&=\ gamma^ {n} +\ gamma^ {n-1} +\ cdots+\ gamma.
\ end {alineado}

Debido a que el esquema es estable, el factor de amplificación satisface\(\gamma \leq 1\). Así, la suma está delimitada por

\(\sum_{j=1}^{n}(1-\lambda \Delta t)^{j-n-1}=\gamma^{n}+\gamma^{n-1}+\cdots+\gamma \leq n \gamma \leq n\)

Así, tenemos

\(\left|e^{n}\right| \leq(n \Delta t)\left\|\tau_{\text {trunc }}\right\|_{\infty}=t^{n}\left\|\tau_{\text {trunc }}\right\|_{\infty}\)

Además, debido a que el esquema es consistente,\(\left\|\tau_{\text {trunc }}\right\|_{\infty} \rightarrow 0\) como\(\Delta t \rightarrow 0\). Por lo tanto,

\(\left\|e^{n}\right\| \leq t^{n}\left\|\tau_{\text {trunc }}\right\|_{\infty} \rightarrow 0 \quad \text { as } \quad \Delta t \rightarrow 0\)

para fijo\(t^{n}=n \Delta t\). Obsérvese que la prueba de convergencia se basa en la estabilidad\((\gamma \leq 1)\) y consistencia\(\left(\left\|\tau_{\text {trunc }}\right\|_{\infty} \rightarrow 0\right.\) como\(\left.\Delta t \rightarrow 0\right)\).

Material Avanzado

Orden de Precisión

El teorema de equivalencia de Dahlquist muestra que si un esquema es consistente y estable, entonces es convergente. Sin embargo, el teorema no establece qué tan rápido el esquema converge a la verdadera solución a medida que se reduce el paso de tiempo. Formalmente, se dice que un esquema es\(p^{\rm th}\) -orden exacto si

\(\left|e^{j}\right|<C \Delta t^{p} \quad \text { for a fixed } t^{j}=j \Delta t \text { as } \Delta t \rightarrow 0 .\)

El esquema de Euler Hacia atrás es preciso de primer orden\((p=1)\), porque

\(\left\|e^{j}\right\| \leq t^{j}\left\|\tau_{\text {trunc }}\right\|_{\infty} \leq t^{j} \frac{\Delta t}{2} \max _{t \in\left[0, t_{f}\right]}\left|\frac{d^{2} u}{d t^{2}}(t)\right| \leq C \Delta t^{1}\)

con

\(C=\frac{t_{f}}{2} \max _{t \in\left[0, t_{f}\right]}\left|\frac{d^{2} u}{d t^{2}}(t)\right|\)

(Nosotros usamos aquí\(t^{j} \leq t_{f}\).)

En general, para un esquema estable, si el error de truncamiento es\(p^{\text {th }}\) -orden exacto, entonces el esquema es\(p^{\text {th }}\) -orden exacto, i.e.

\(\left\|\tau_{\text {trunc }}\right\|_{\infty} \leq C \Delta t^{p} \quad \Rightarrow \quad\left|e^{j}\right| \leq C \Delta t^{p} \quad \text { for a fixed } t^{j}=j \Delta t\)

Es decir, una vez que probamos la estabilidad de un esquema, entonces solo necesitamos analizar su error de truncamiento para entender su tasa de convergencia. Esto requiere poco más trabajo que verificar la consistencia. Es significativamente más sencillo que derivar la expresión para la evolución del error y analizar el comportamiento del error directamente.

La Figura 21.4 muestra el comportamiento de convergencia de errores del esquema Euler hacia atrás aplicado a la ODE homogénea con\(λ = −4\). El error se mide en\(t = 1\). Consistente con la teoría, el esquema converge a razón de\(p = 1\).

Esquema explícito: Euler Forward

Introduzcamos ahora un nuevo esquema, el esquema de Euler Forward. El esquema Euler Forward se obtiene aplicando la fórmula de diferencia hacia adelante de primer orden a la derivada de tiempo, i.e.

\(\dfrac{du}{dt} \approx \dfrac{\tilde{u}^{j+1} - \tilde{u}^j}{\Delta t}\).

Figura 21.4: El comportamiento de convergencia de errores para el esquema de Euler hacia atrás aplicado a la ODE homogénea\((λ = −4)\). Nota\(e(t = 1) = |u(t^j ) − \tilde{u}^j |\) en\(t^j = j∆t = 1\).

La sustitución de la expresión por la ODE lineal produce una ecuación de diferencia,

\ begin {alineado}
\ frac {\ tilde {u} ^ {j+1} -\ tilde {u} ^ {j}} {\ Delta t} &=\ lambda\ tilde {u} ^ {j} +f\ izquierda (t^ {j}\ derecha),\ quad j=0,\ ldots, J-1
\\ tilde {u} ^ {0} &=u_ 0}
\ end {alineado}

Para mantener el mismo índice de tiempo que el esquema de Euler hacia atrás (es decir, la ecuación de diferencia involucra las incógnitas\(\tilde{u}^{j}\) y\(\tilde{u}^{j-1}\)), desplazemos los índices para obtener

\ begin {alineado}
\ frac {\ tilde {u} ^ {j} -\ tilde {u} ^ {j-1}} {\ Delta t} &=\ lambda\ tilde {u} ^ {j-1} +f\ izquierda (t^ {j-1}\ derecha),\ quad j=1,\ ldots, J,\
\ tilde {u} ^ {0} &=u_ {0}.
\ end {alineado}

La diferencia clave con respecto al esquema de Euler Hacia atrás es que los términos del lado derecho se evalúan en\(t^{j-1}\) lugar de at\(t^{j}\). Los esquemas para los que el lado derecho no implica nivel de tiempo\(j\) se conocen como esquemas “explícitos”. Si bien el cambio puede parecer menor, esto modifica significativamente la estabilidad. (También cambia la complejidad computacional, como discutiremos más adelante.) Podemos ver a Euler Forward como una especie de regla de integración “rectángulo, izquierda”.

Analicemos ahora la consistencia y estabilidad del esquema. La prueba de consistencia es similar a la del esquema Atrás de Euler. El error de truncamiento para el esquema es

\(\tau_{\text {trunc }}^{j}=\frac{u\left(t^{j}\right)-u\left(t^{j-1}\right)}{\Delta t}-\lambda u\left(t^{j-1}\right)-f\left(t^{j-1}\right) .\)

Para analizar la convergencia del error de truncamiento, aplicamos la expansión de Taylor\(t^{j-1}\) a\(u\left(t^{j}\right)\) aproximadamente para obtener,

\(u\left(t^{j}\right)=u\left(t^{j-1}\right)+\Delta t \frac{d u}{d t}\left(t^{j-1}\right)+\underbrace{\int_{t^{j-1}}^{t^{j}}\left(\int_{t^{j-1}}^{\tau} \frac{d u^{2}}{d t^{2}}(\gamma) d \gamma\right) d \tau}_{s^{j}(u)}\)

Por lo tanto, el error de truncamiento simplifica a

\ begin {alineado}
\ tau_ {\ text {trunc}} ^ {j} &=\ frac {1} {\ Delta t}\ left (u\ left (t^ {j-1}\ right) +\ Delta t\ frac {d u} {d t}\ left (t^ {j-1}\ right) +s^ {j} (u) -u\ left (t^ {j-1}\ right) +s^ {j} (u) -u\ left (t^ {j-1}\ right -1}\ derecha)\ derecha)\\
&=\ underbrackets {\ frac {d u} {d t}\ izquierda (t^ {j-1}\ derecha) -\ lambda u\ izquierda (t^ {j-1}\ derecha) -f\ izquierda (t^ {j-1}\ derecha )} _ {=0:\ text {por ODE}} +\ frac {s^ {j} (u)} {\ Delta t}\\
&=\ frac {s^ {j} (u)} {\ Delta t}.
\ end {alineado}

Al probar la consistencia del esquema de Euler Atrás, hemos demostrado que\(s^{j}(u)\) está delimitado por

\(s^{j}(u) \leq \max _{t \in\left[t^{j-1}, t^{j}\right]}\left|\frac{d^{2} u}{d t^{2}}(t)\right| \frac{\Delta t^{2}}{2}, \quad j=1, \ldots, J .\)

Por lo tanto, el error de truncamiento máximo está limitado por

\(\left\|\tau_{\text {trunc }}\right\|_{\infty} \leq \max _{t \in\left[0, t_{f}\right]}\left|\frac{d^{2} u}{d t^{2}}(t)\right| \frac{\Delta t}{2} .\)

Nuevamente, el error de truncamiento converge linealmente con $\ Delta t$ y el esquema es consistente porque\(\left\|\tau_{\text {trunc }}\right\|_{\infty} \rightarrow 0\) as\(\Delta t \rightarrow 0\). Debido a que el esquema es consistente, solo necesitamos demostrar que es estable para asegurar la convergencia.

Para analizar la estabilidad del esquema, calculemos el factor de amplificación. Reordenando la ecuación de diferencia para el caso homogéneo,

\(\tilde{u}^{j}-\tilde{u}^{j-1}=\lambda \Delta t \tilde{u}^{j-1}\)

o

\(\left|\tilde{u}^{j}\right|=|1+\lambda \Delta t|\left|\tilde{u}^{j-1}\right|\)

que da

\(\gamma=|1+\lambda \Delta t|\)

Por lo tanto, la estabilidad absoluta (i.e.,\(\gamma \leq 1\)) requiere

\ begin {alineado}
&-1\ leq 1+\ lambda\ Delta t\ leq 1\\
&-2\ leq\ lambda\ Delta t\ leq 0
\ end {alineado}

Observar\(\lambda \Delta t \leq 0\) es una condición trivial para\(\lambda<0\), la condición para la estabilidad es

\(\Delta t \leq-\frac{2}{\lambda} \equiv \Delta t_{\mathrm{cr}}\)

Tenga en cuenta que el esquema de Euler Forward es estable sólo para\(\Delta t \leq 2 /|\lambda|\). Así, el esquema es condicionalmente estable. Recordando la estabilidad es una condición necesaria para la convergencia, concluimos que el esquema converge para\(\Delta t \leq \Delta t_{\text {cr }}\), pero diverge (es decir, estalla) con\(j\) si\(\Delta t>\Delta t_{\text {cr }}\).

La Figura 21.5 muestra el comportamiento de convergencia de errores del esquema Euler Forward aplicado a la ODE homogénea con\(\lambda=-4\). El error se mide en\(t=1\). El paso de tiempo crítico para la estabilidad es\(\Delta t_{\mathrm{cr}}=-2 / \lambda=1 / 2\). La gráfica de convergencia de errores muestra que el error crece exponencialmente para

Figura 21.5: El comportamiento de convergencia de errores para el esquema Euler Forward aplicado a\(d u / d t=-4 u\). Nota\(e(t=1)=\left|u\left(t^{j}\right)-\tilde{u}^{j}\right|\) en\(t^{j}=j \Delta t=1\).

\(∆t > 1/2\). Como\(∆t\) tiende a cero, la aproximación numérica converge a la solución exacta, y la tasa de convergencia (orden) es\(p = 1\) — consistente con la teoría. Cabe destacar que la inestabilidad del esquema de Euler Forward para no\(∆t > ∆t_{\rm cr}\) se debe a errores de redondeo y representación en punto flotante (lo que implica “truncamiento”, pero no truncamiento de la variedad discutida en este capítulo). En particular, todos nuestros argumentos a favor de la inestabilidad se mantienen tanto en la aritmética de precisión infinita como en la aritmética de precisión finita. La inestabilidad deriva de la ecuación de diferencia; la inestabilidad amplifica el error de truncamiento, que es una propiedad de la ecuación de diferencia y la ecuación diferencial. Por supuesto, una ecuación de diferencia inestable amplificará también los errores de redondeo, pero esa es una consideración adicional y no la razón principal de la explosión en la Figura 21.5.

Ecuaciones rígidas: implícitas vs. explícitas

Las ecuaciones rígidas son la clase de ecuaciones que exhiben una amplia gama de escalas de tiempo. Por ejemplo, recuerde la ODE lineal con un forzamiento sinusoidal,

\(\dfrac{du}{dt} = \lambda t + cos(ωt)\),

con\(|λ| >> ω\). La respuesta transitoria de la solución viene dictada por la constante de tiempo\(1/|λ|\). Sin embargo, este transitorio inicial decae exponencialmente con el tiempo. La respuesta de largo tiempo se rige por la constante de tiempo\(1/ω >> 1/|λ|\).

Consideremos el caso con\(λ = −100\) y\(ω = 4\); las escalas de tiempo difieren en un factor de 25. El resultado de aplicar los esquemas Euler Atrás y Euler Adelante con varios pasos de tiempo diferentes se muestra en la Figura 21.6. Recordemos que el esquema de Euler Hacia atrás es estable para cualquier paso de tiempo para\(λ < 0\). El resultado numérico confirma que la solución está delimitada para todos los pasos de tiempo considerados. Mientras que un paso de tiempo grande (en particular\(∆t > 1/|λ|\)) da como resultado una aproximación que no captura el transitorio inicial, el comportamiento a largo plazo de la solución todavía está bien representado. Así, si el transitorio inicial no es de interés, podemos usar un ∆t optimizado para resolver solo el comportamiento a largo plazo asociado con la escala de tiempo característica de\(1/ω\) — en otras palabras,\(∆t ∼ O(1/10)\),

Figura 21.6: Aplicación de los esquemas Euler Atrás y Adelante de Euler a una ecuación rígida. Nota\(e(t = 1) = |u(t^j ) − \tilde{u}^j |\) en\(t^j = j∆t = 1\).

en lugar de\(∆t ∼ O(1/|λ|)\). Si\(|λ| >> ω\), entonces reducimos significativamente el número de pasos de tiempo (y por lo tanto el costo computacional).

A diferencia de su contraparte implícita, el método de Euler Forward sólo es condicionalmente estable. En particular, el paso crítico de tiempo para este problema lo es\(∆t_{\rm cr} = 2/|λ| = 0.02\). Así, aunque no nos interese el transitorio inicial, no podemos usar un paso de tiempo grande porque el esquema sería inestable. Solo una de las tres soluciones numéricas (\(∆t = 1/64 < ∆t_{\rm cr}\)) se muestra en la Figura 21.6 (c) porque los otros dos pasos de tiempo (\(∆t = 1/16, ∆t = 1/4\)) dan como resultado una discretización inestable y una aproximación inútil. El crecimiento exponencial del error para\(∆t > ∆t_{\rm cr}\) se refleja claramente en la Figura 21.6 (d).

Las ecuaciones rígidas son ubicuas en el contexto de la ciencia y la ingeniería; de hecho, no es raro ver escalas que difieren en más de diez órdenes de magnitud. Por ejemplo, la escala de tiempo asociada con la dinámica de un avión de pasajeros es varios órdenes de magnitud mayor que la escala de tiempo asociada con remolinos turbulentos. Si la dinámica de la escala de tiempo más pequeña no es de interés, entonces un esquema incondicionalmente estable que nos permita dar pasos de tiempo arbitrariamente grandes puede ser computacionalmente ventajoso. En particular, podemos seleccionar el paso de tiempo que sea necesario para lograr una precisión suficiente sin ninguna restricción de paso de tiempo derivada de la consideración de estabilidad. Dicho de otra manera, la integración de un sistema rígido utilizando un método condicionalmente estable puede establecer un requisito estricto en el paso de tiempo, haciendo que la integración sea prohibitivamente costosa. Como ninguno de los esquemas explícitos es incondicionalmente estable, a menudo se prefieren esquemas implícitos para ecuaciones rígidas.

De lo anterior podríamos concluir que los esquemas explícitos tienen muy poco propósito. De hecho, no es así, porque la historia es un poco más complicada. En particular, observamos que para Euler Hacia atrás, en cada paso de tiempo, debemos efectuar una operación de división,\(1/(1−(λ∆t))\), mientras que para Euler Adelante debemos efectuar una multiplicación,\(1 + (λ∆t)\). Cuando consideramos problemas reales de interés —sistemas, a menudo sistemas grandes, de muchas y a menudo no lineales ODEs— estas operaciones algebraicas escalares de división para esquemas implícitos y multiplicación para esquemas explícitos se traducirán en inversión matricial (más precisamente, solución de ecuaciones matriciales) y matriz multiplicación, respectivamente. En general, y como veremos en la Unidad V, la inversión matricial es mucho más costosa que la multiplicación matricial.

De ahí que la ecuación del costo total sea más matizada. Un esquema implícito normalmente disfrutará de un paso de tiempo más grande y, por lo tanto, menos pasos de tiempo, pero requerirá más trabajo para cada paso de tiempo (solución de matriz). Por el contrario, un esquema explícito puede requerir un paso de tiempo mucho más pequeño y, por lo tanto, muchos más pasos de tiempo, pero implicará mucho menos trabajo para cada paso de tiempo. Para ecuaciones rígidas en las que la\(∆t\) precisión es mucho, mucho mayor que la\(∆t_{\rm cr}\) requerida para la estabilidad (de esquemas explícitos), generalmente gana implícita. Por otro lado, para ecuaciones no rígidas, en las que la\(∆t\) precisión podría estar en el mismo orden que se\(∆t_{\rm cr}\) requiere para la estabilidad (de esquemas explícitos), explícito a menudo puede ganar: en tales casos elegiríamos en cualquier caso (por razones de precisión) un\(∆t \approx ∆t_{\rm cr}\); de ahí, ya que un esquema explícito lo hará ser estables para esto\(∆t\), también podríamos elegir un esquema explícito para minimizar el trabajo por paso de tiempo.

Ecuaciones inestables

Diagramas de estabilidad y estabilidad absolutas

Hemos aprendido que diferentes esquemas de integración presentan diferentes características de estabilidad. En particular, los métodos implícitos tienden a ser más estables que los métodos explícitos. Para caracterizar la estabilidad de diferentes integradores numéricos, introduzcamos diagramas de estabilidad absoluta. Estos diagramas nos permiten analizar rápidamente si un esquema de integración será estable para un sistema dado.

Euler hacia atrás

Construyamos el diagrama de estabilidad para el esquema Atrás de Euler. Comenzamos con la ecuación homogénea

\(\dfrac{dz}{dt} = \lambda z\).

Hasta el momento, sólo hemos considerado un real\(λ\); ahora permitimos\(λ\) ser un número complejo general. (Posteriormente\(λ\) representará un valor propio de un sistema, que en general será un número complejo). El Euler

Figura 21.7: El diagrama de estabilidad absoluta para el esquema Atrás de Euler.

La discretización hacia atrás de la ecuación es

\(\frac{\tilde{z}^{j}-\tilde{z}^{j-1}}{\Delta t}=\lambda \tilde{z}^{j} \Rightarrow \quad \tilde{z}^{j}=(1-(\lambda \Delta t))^{-1} \tilde{z}^{j-1}\)

Recordemos que definimos la estabilidad absoluta como la región en la que el factor de amplificación\(\gamma \equiv\)\(\left|\tilde{z}^{j}\right| /\left|\tilde{z}^{j-1}\right|\) es menor o igual a la unidad. Esto requiere

\(\gamma=\frac{\left|\tilde{z}^{j}\right|}{\left|\tilde{z}^{j-1}\right|}=\left|\frac{1}{1-(\lambda \Delta t)}\right| \leq 1\)

Deseamos encontrar los valores\((\lambda \Delta t)\) para los cuales la solución numérica exhibe un comportamiento estable (i.e.,\(\gamma \leq 1\)). Un enfoque simple para lograr esto es resolver el límite de estabilidad estableciendo el factor de amplificación en\(1=\left|e^{i \theta}\right|\), i.e.

\(e^{i \theta}=\frac{1}{1-(\lambda \Delta t)}\)

Resolviendo para\((\lambda \Delta t)\), obtenemos

\((\lambda \Delta t)=1-e^{-i \theta}\)

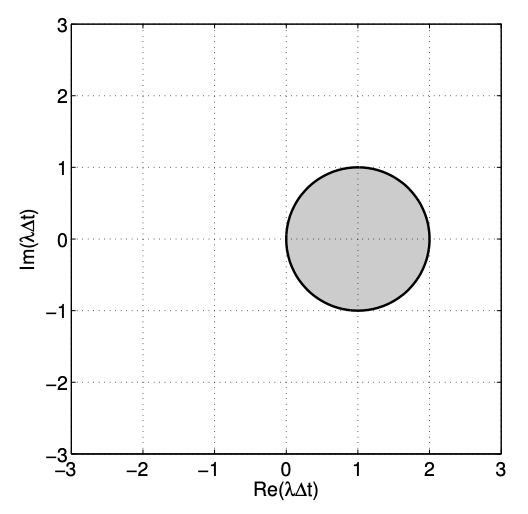
Así, el límite de estabilidad para el esquema de Euler Hacia atrás es un círculo de radio unitario (el “uno” que se multiplica\(e^{i \theta}\)) centrado en 1 (el que está directamente después del\(=\operatorname{sign}\)).

Para deducir en qué lado del límite el esquema es estable, podemos verificar el factor de amplificación evaluado en un punto no en el círculo. Por ejemplo, si elegimos\(\lambda \Delta t=-1\), lo observamos\(\gamma=1 / 2 \leq 1\). Así, el esquema es estable fuera del círculo unitario. La Figura 21.7 muestra el diagrama de estabilidad para el esquema de Euler hacia atrás. El esquema es inestable en la región sombreada; es estable en la región no sombreada; es neutralmente estable,\(\left|\tilde{z}^{j}\right|=\left|\tilde{z}^{j-1}\right|\), en el círculo unitario. La región no sombreada\((\gamma<1)\) y el límite de las regiones sombreadas y no sombreadas\((\gamma=1)\) representan la región de estabilidad absoluta; toda la imagen se denota el diagrama de estabilidad absoluta.

Para comprender el diagrama de estabilidad, consideremos el comportamiento del esquema de Euler hacia atrás para unos pocos valores selectos de\(\lambda \Delta t\). Primero, consideramos una ecuación homogénea estable, con\(\lambda=-1<0\). Consideramos tres valores diferentes de\(\lambda \Delta t,-0.5,-1.7\), y\(-2.2\). La Figura 21.8 (a) muestra

Figura 21.8: El comportamiento del esquema hacia atrás de Euler para valores seleccionados de\((λ∆t)\).

los tres puntos en el diagrama de estabilidad que corresponden a estas elecciones de\(λ∆t\). Los tres puntos se encuentran en la región sin sombra, que es una región estable. La Figura 21.8 (b) muestra que las tres soluciones numéricas disminuyen con el tiempo como se esperaba. Mientras que el menor\(∆t\) da como resultado un error menor, todos los esquemas son estables y convergen a la misma solución de estado estacionario.

Comenzar material avanzado

A continuación, consideramos una ecuación homogénea inestable, con\(λ = 1 > 0\). De nuevo consideramos tres valores diferentes de\(λ∆t, 0.5, 1.7\), y la\(2.2.\) Figura 21.8 (c) muestra que dos de estos puntos se encuentran en la región inestable, mientras que\(λ∆t = 2.2\) se encuentra en la región estable. La Figura 21.8 (d) confirma que las soluciones para\(λ∆t = 0.5\) y\(1.7\) crecen con el tiempo, mientras que\(λ∆t = 2.2\) da como resultado una solución en descomposición. La verdadera solución, por supuesto, crece exponencialmente con el tiempo. Así, si el paso de tiempo es demasiado grande (específicamente\(λ∆t > 2\)), entonces el esquema de Euler hacia atrás puede producir una solución en descomposición aunque la verdadera solución crezca con el tiempo —lo cual es indeseable; sin embargo\(∆t \rightarrow 0\), como, obtenemos el comportamiento correcto. En general, el interior de la región de estabilidad absoluta no debe incluir\(λ∆t = 0\). (De hecho\(λ∆t = 0\) debería estar en el límite de estabilidad.)

Figura 21.9: El diagrama de estabilidad absoluta para el esquema Euler Forward. El área blanca corresponde a la estabilidad (la región de estabilidad absoluta) y el área gris a la inestabilidad.

Material Avanzado

Euler Delantero

Analicemos ahora las características de estabilidad absoluta del esquema Euler Forward. Similar al esquema de Euler Hacia atrás, comenzamos con la ecuación homogénea. La discretización de Euler Forward de la ecuación rinde

\(\dfrac{\tilde{z}^j - \tilde{z}^{j-1}}{\Delta t} = \lambda \tilde{z}^{j-1} \Rightarrow \tilde{z}^j = \left ( 1 + (\lambda \Delta t) \right) \tilde{z}^{j-1}\).

El límite de estabilidad, en el que el factor de amplificación es la unidad, viene dado por

\(\gamma = |1 + (\lambda \Delta t)| = 1 \Rightarrow (\lambda \Delta t) = e^{-i \Theta} - 1\)

El límite de estabilidad es un círculo de radio unitario centrado en\(−1\). La sustitución de, por ejemplo,\(λ∆t = −1/2\), rinde\(\gamma(λ∆t = −1/2) = 1/2\), por lo que la amplificación es menor que la unidad dentro del círculo. El diagrama de estabilidad para el esquema Euler Forward se muestra en la Figura 21.9.

Al igual que en el caso de Euler Hacia atrás, escojamos algunos valores selectos de λ∆t y estudiemos el comportamiento del esquema Euler Forward. El diagrama de estabilidad y el comportamiento de la solución para una ODE estable (\(λ = −1 < 0\)) se muestran en la Figura 21.10 (a) y 21.10 (b), respectivamente. Los casos con\(λ∆t = −0.5\) y\(−1.7\) se encuentran en la región estable del diagrama de estabilidad, mientras que\(λ∆t = −2.2\) se encuentran en la región inestable. Debido a la inestabilidad, la solución numérica para\(λ∆t = −2.2\) diverge exponencialmente con el tiempo, a pesar de que la verdadera solución decae con el tiempo. La solución para\(λ∆t = −1.7\) muestra cierta oscilación, pero la magnitud de la oscilación decae con el tiempo, coincidiendo con el diagrama de estabilidad. (Para una ODE inestable (\(λ = 1 > 0\)), la Figura 21.10 (c) muestra que todos los pasos de tiempo considerados se encuentran en la región inestable del diagrama de estabilidad. La Figura 21.10 (d) confirma que todas estas elecciones de ∆t producen una solución de crecimiento.)

Esquemas multipaso

Hasta el momento hemos considerado dos esquemas: el esquema Euler Atrás y el esquema Euler Forward. Estos dos esquemas computan el estado\(\tilde{u}^j\) a partir del estado anterior\(\tilde{u}^{j−1}\) y la función de origen

Figura 21.10: El comportamiento del esquema Euler Forward para valores seleccionados de\(λ∆t\).

evaluado en\(t^j\) o\(t^{j−1}\). Los dos esquemas son casos especiales de esquemas multipaso, donde la solución en el momento actual\(\tilde{u}^j\) se aproxima a partir de las soluciones anteriores. En general, para una ODE de la forma

\(\dfrac{du}{dt} = g(u,t)\),

un esquema\(K\) multipaso -paso toma la forma

\ begin {alineado}
\ sum_ {k=0} ^ {K}\ alpha_ {k}\ tilde {u} ^ {j-k} &=\ Delta t\ sum_ {k=0} ^ {K}\ beta_ {k} g^ {j-k},\ quad j=1\
\ tilde {u} ^ {j} &=u_ {0}
\ end {alineado}

donde\(g^{j-k}=g\left(\tilde{u}^{j-k}, t^{j-k}\right)\). Tenga en cuenta que la ODE lineal hemos estado considerando los resultados de la elección\(g(u, t)=\lambda u+f(t)\). Un esquema\(K\) multipaso -paso requiere soluciones (y derivados) en etapas de tiempo\(K\) anteriores. Sin pérdida de generalidad, elegimos\(\alpha_{0}=1\). Un esquema se define de manera única eligiendo\(2 K+1\) coeficientes,\(\alpha_{k}, k=1, \ldots, K\), y\(\beta_{k}, k=0, \ldots, K\).

Los esquemas multipaso se pueden clasificar en esquemas implícitos y explícitos. Si elegimos\(\beta_{0}=0\), entonces\(\tilde{u}^{j}\) no aparece en el lado derecho, resultando en un esquema explícito. Como se discutió anteriormente, los esquemas explícitos solo son condicionalmente estables, pero son computacionalmente menos costosos por paso. Si elegimos\(\beta_{0} \neq 0\), entonces\(\tilde{u}^{j}\) aparece en el lado derecho, dando como resultado un esquema implícito. Los esquemas implícitos tienden a ser más estables, pero son más costosos computacionalmente por paso, especialmente para un sistema de ODEs no lineales.

Reformemos los esquemas Euler Atrás y Euler Forward en el marco del método multipaso.

Ejemplo 21.1.2 Euler Hacia atrás como esquema de varios pasos

El esquema Euler Backward es un método de 1 paso con las opciones

\(\alpha_{1}=-1, \quad \beta_{0}=1, \quad \text { and } \quad \beta_{1}=0 .\)

Esto da como resultado

\(\tilde{u}^{j}-\tilde{u}^{j-1}=\Delta t g^{j}, \quad j=1, \ldots, J\)

______________________ . ______________________

Ejemplo 21.1.3 Euler Forward como esquema multipaso

El esquema Euler Forward es un método de 1 paso con las opciones

\(\alpha_{1}=-1, \quad \beta_{0}=0, \quad \text { and } \quad \beta_{1}=1 .\)

Esto da como resultado

\(\tilde{u}^{j}-\tilde{u}^{j-1}=\Delta t g^{j-1}, \quad j=1, \ldots, J\)

______________________ . ______________________

Ahora consideramos tres familias de esquemas multipaso: Adams-Bashforth, Adams-Moulton y Fórmulas de diferenciación hacia atrás.

Esquemas de Adams-Bashforth

Los esquemas Adams-Bashforth son esquemas explícitos de integración de tiempo multipaso\(\left(\beta_{0}=0\right)\). Además, nos limitamos a

\(\alpha_{1}=-1 \quad \text { and } \quad \alpha_{k}=0, \quad k=2, \ldots, K .\)

La familia resultante de los esquemas toma la forma

\(\tilde{u}^{j}=\tilde{u}^{j-1}+\sum_{k=1}^{K} \beta_{k} g^{j-k}\)

Ahora debemos elegir\(\beta_{k}, k=1, \ldots K\), definir un esquema. Para elegir los valores apropiados de\(\beta_{k}\), primero observamos que la verdadera solución\(u\left(t^{j}\right)\) y\(u\left(t^{j-1}\right)\) están relacionados por

\[u\left(t^{j}\right)=u\left(t^{j-1}\right)+\int_{t^{j-1}}^{t^{j}} \frac{d u}{d t}(\tau) d \tau=u\left(t^{j-1}\right)+\int_{t^{j-1}}^{t^{j}} g(u(\tau), \tau) d \tau . \tag{21.1} \]

Entonces, aproximamos el integrando\(g(u(\tau), \tau), \tau \in\left(t^{j-1}, t^{j}\right)\), usando los valores\(g^{j-k}, k=1, \ldots, K\). Específicamente, construimos un polinomio de\((K-1)^{\text {th }}\) grado\(p(\tau)\) usando los puntos de\(K\) datos, i.e.

\(p(\tau)=\sum_{k=1}^{K} \phi_{k}(\tau) g^{j-k}\),

donde\(\phi_{k}(\tau), k=1, \ldots, K\), son los polinomios de interpolación de Lagrange definidos por los puntos\(t^{j-k}, k=1, \ldots, K\). Recordando la teoría de interpolación polinómica de la Unidad I, observamos que el interpolante polinomio de\((K-1)^{\text {th }}\) grado es\(K^{\text {th }}\) -orden exacto para\(g(u(\tau), \tau)\) suficientemente suave, i.e.

\(p(\tau)=g(u(\tau), \tau)+\mathcal{O}\left(\Delta t^{K}\right) .\)

(Nota de hecho aquí consideramos “extrapolación” de nuestro interpolante.) Así, esperamos que el orden de aproximación mejore a medida que incorporemos más puntos dada la suficiente suavidad. La sustitución de la aproximación polinómica de la derivada a la Ec. (21.1) rinde

\(u\left(t^{j}\right) \approx u\left(t^{j-1}\right)+\int_{t^{j-1}}^{t^{j}} \sum_{k=1}^{K} \phi_{k}(\tau) g^{j-k} d \tau=u\left(t^{j-1}\right)+\sum_{k=1}^{K} \int_{t^{j-1}}^{t^{j}} \phi_{k}(\tau) d \tau g^{j-k} .\)

Para simplificar la integral, consideremos el cambio de variable\(\tau=t^{j}-\left(t^{j}-t^{j-1}\right) \hat{\tau}=t^{j}-\Delta t \hat{\tau}\). El cambio de rendimientos variables

\(u\left(t^{j}\right) \approx u\left(t^{j-1}\right)+\Delta t \sum_{k=1}^{K} \int_{0}^{1} \hat{\phi}_{k}(\hat{\tau}) d \hat{\tau} g^{j-k}\)

donde\(\hat{\phi}_{k}\) son los polinomios de Lagrange asociados con los puntos de interpolación\(\hat{\tau}=1,2, \ldots, K\). Reconocemos que la aproximación se ajusta a la forma Adams-Bashforth si elegimos

\(\beta_{k}=\int_{0}^{1} \hat{\phi}_{k}(\hat{\tau}) d \hat{\tau} \).

Desarrollemos algunos ejemplos de esquemas Adams-Bashforth.

Ejemplo 21.1.4 Adams-Bashforth de 1 paso (Adelante de Euler)

El esquema Adams-Bashforth de 1 paso requiere la evaluación de\(\beta_{1}\). El polinomio Lagrange para este caso es un polinomio constante,\(\hat{\phi}_{1}(\hat{\tau})=1\). Así, obtenemos

\(\beta_{1}=\int_{0}^{1} \hat{\phi}_{1}(\hat{\tau}) d \hat{\tau}=\int_{0}^{1} 1 d \hat{\tau}=1\).

Así, el esquema es

\(\tilde{u}^j = \tilde{u}^{j-1} + \Delta t g^{j-1}\),

que es el esquema Euler Forward, preciso de primer orden.

______________________ . ______________________

Ejemplo 21.1.5 Adams-Bashforth de 2 pasos

El esquema Adams-Bashforth de 2 pasos requiere la especificación de\(\beta_1\) y\(\beta_2\). Los polinomios de interpolación de Lagrange para este caso son polinomios lineales

\(\hat{\phi}_{1}(\hat{\tau})=-\hat{\tau}+2 \quad$ and $\quad \hat{\phi}_{2}(\hat{\tau})=\hat{\tau}-1\)

Es fácil verificar que estos son los polinomios de Lagrange porque\(\hat{\phi}_{1}(1)=\hat{\phi}_{2}(2)=1\) y\(\hat{\phi}_{1}(2)=\hat{\phi}_{2}(1)=0\). Integrando los polinomios

\ begin {alineado}
&\ beta_ {1} =\ int_ {0} ^ {1}\ phi_ {1} (\ hat {\ tau}) d\ hat {\ tau} =\ int_ {0} ^ {1} (-\ hat {\ tau} +2) d\ hat {\ tau} =\ frac {3} {2},\\
&\ beta_ {2} =\ int_ {0} ^ {1}\ phi_ {2} (\ hat {\ tau}) d\ hat {\ tau} =\ int_ {0} ^ {1} (\ hat {\ tau} -1) d\ sombrero {\ tau} =-\ frac {1} {2}
\ end {alineado}

El esquema resultante es

\(\tilde{u}^{j}=\tilde{u}^{j-1}+\Delta t\left(\frac{3}{2} g^{j-1}-\frac{1}{2} g^{j-2}\right) .\)

Este esquema es preciso de segundo orden.

______________________ . ______________________

Esquemas Adams-Moulton

Los esquemas Adams-Moulton son esquemas implícitos de integración de tiempo multipaso\(\left(\beta_{0} \neq 0\right)\). Similar a los esquemas Adams-Bashforth, nos limitamos a

\(\alpha_{1}=-1 \quad \text { and } \quad \alpha_{k}=0, \quad k=2, \ldots, K .\)

La familia Adams-Moulton de los esquemas toma la forma

\(\tilde{u}^{j}=\tilde{u}^{j-1}+\sum_{k=0}^{K} \beta_{k} g^{j-k}\)

Debemos optar\(\beta_{k}, k=1, \ldots, K\) por definir un esquema. La elección de\(\beta_{k}\) sigue exactamente el mismo procedimiento que el de Adams-Bashforth. A saber, consideramos la expansión de la forma Ec. (21.1) y aproximada\(g(u(\tau), \tau)\) por un polinomio. Esta vez, tenemos\(K+1\) puntos, así construimos un polinomio de\(K^{\text {th }}\) grado

\(p(\tau)=\sum_{k=0}^{K} \phi_{k}(\tau) g^{j-k},\)

donde\(\phi_{k}(\tau), k=0, \ldots, K\), son los polinomios de interpolación de Lagrange definidos por los puntos\(t^{j-k}\),\(k=0, \ldots, K\). Tenga en cuenta que estos polinomios son diferentes a los de los esquemas Adams-Bashforth debido a la inclusión de\(t^{j}\) como uno de los puntos de interpolación. (De ahí que aquí consideremos la verdadera interpolación, no la extrapolación.) Además, la interpolación ahora es precisa\((K+1)^{\text {th }}\) de orden.

Usando el mismo cambio de variable que para los esquemas Adams-Bashforth\(\tau=t^{j}-\Delta t \hat{\tau}\),, llegamos a una expresión similar,

\(u\left(t^{j}\right) \approx u\left(t^{j-1}\right)+\Delta t \sum_{k=0}^{K} \int_{0}^{1} \hat{\phi}_{k}(\hat{\tau}) d \hat{\tau} g^{j-k}\)

para los esquemas Adams-Moulton; aquí\(\hat{\phi}_{k}\) están los polinomios de Lagrange\(K^{\text {th }}\) -grado definidos por los puntos\(\hat{\tau}=0,1, \ldots, K\). Así, los\(\beta_{k}\) son dados por

\(\beta_{k}=\int_{0}^{1} \hat{\phi}_{k}(\hat{\tau}) d \hat{\tau} .\)

Desarrollemos algunos ejemplos de esquemas Adams-Moulton.

Ejemplo 21.1.6 Adams-Moulton de 0 pasos (Euler hacia atrás)

El esquema Adams-Moulton de 0 pasos requiere solo un coeficiente,\(\beta_{0}\). El polinomio “Lagrange” es\(0^{\text {th }}\) grado, es decir, una función constante\(\hat{\phi}_{0}(\hat{\tau})=1\), y la integración de la función constante sobre el intervalo unitario rinde

\(\beta_{0}=\int_{0}^{1} \hat{\phi}_{0}(\hat{\tau}) d \hat{\tau}=\int_{0}^{1} 1 d \hat{\tau}=1 .\)

Así, el esquema Adams-Moulton de 0 pasos viene dado por

\(\tilde{u}^{j}=\tilde{u}^{j-1}+\Delta t g^{j},\)

que de hecho es el esquema de Euler Atrás. Recordemos que el esquema de Euler Backward es preciso de primer orden.

______________________ . ______________________

Ejemplo 21.1.7 Adams-Moulton de 1 paso (Crank-Nicolson)

El esquema Adams-Moulton de 1 paso requiere la determinación de dos coeficientes,\(\beta_0\) y\(\beta_1\). Los polinomios de Lagrange para este caso son polinomios lineales

\(\hat{\phi}_{0}(\hat{\tau})=-\tau+1 \quad$ and $\quad \hat{\phi}_{1}(\hat{\tau})=\tau\)

Integrando los polinomios,

\ begin {alineado}
&\ beta_ {0} =\ int_ {0} ^ {1}\ hat {\ phi} _ {0} (\ hat {\ tau}) d\ hat {\ tau} =\ int_ {0} ^ {1} (-\ tau+1) d\ hat {\ tau} =\ frac {1} {2}\\
&\ beta_ {1}\ int_ {0} ^ {1}\ sombrero {\ phi} _ {1} (\ sombrero {\ tau}) d\ sombrero {\ tau} =\ int_ {0} ^ {1}\ sombrero {\ tau} d\ sombrero {\ tau} =\ frac {1} {2}
\ fin {alineado}

La elección de\(\beta_{k}\) rendimientos el esquema Crank-Nicolson

\(\tilde{u}^{j}=\tilde{u}^{j-1}+\Delta t\left(\frac{1}{2} g^{j}+\frac{1}{2} g^{j-1}\right)\).

El esquema Crank-Nicolson es preciso de segundo orden. Podemos ver a Crank-Nicolson como una especie de regla “trapezoidal”.

______________________ . ______________________

Ejemplo 21.1.8 Adams-Moulton de 2 pasos

El esquema Adams-Moulton de 2 pasos requiere tres coeficientes,\(\beta_{0}, \beta_{1}\), y\(\beta_{2}\). Los polinomios de Lagrange para este caso son los polinomios cuadráticos

\ begin {alineado}
&\ hat {\ phi} _ {0} (\ hat {\ tau}) =\ frac {1} {2} (\ hat {\ tau} -1) (\ hat {\ tau} -2) =\ frac {1} {2}\ left (\ hat {\ tau} ^ {2} -3\ hat {\ tau}\ right. \\
&\ sombrero {\ phi} _ {1} (\ sombrero {\ tau}) =-\ sombrero {\ tau} (\ sombrero {\ tau} -2) =-\ sombrero {\ tau} ^ {2} +2\ sombrero {\ tau}\\
&\ sombrero {\ phi} _ {2} (\ sombrero {\ tau}) =\ frac {1} {2}\ sombrero {\ tau} (\ sombrero {\ tau} -1) =\ frac {1} {2}\ izquierda (\ sombrero {\ tau} ^ {2} -\ sombrero {\ tau}\ derecha)
\ fin {alineado}

Integrando los polinomios,

\ begin {alineado}
&\ beta_ {0} =\ int_ {0} ^ {1}\ sombrero {\ phi} _ {0} (\ hat {\ tau}) d\ hat {\ tau} =\ int_ {0} ^ {1}\ frac {1} {2}\ izquierda (\ sombrero {\ tau} ^ {2} -3\ sombrero {\ tau} +2\ derecha)\ sombrero {\ tau} =\ frac {5} {12}\\
&\ beta_ {1} =\ int_ {0} ^ {1}\ sombrero {\ phi} _ {1} (\ sombrero {\ tau}) d\ sombrero {\ tau} =\ int_ {0} ^ {1}\ izquierda (-\ sombrero {\ tau} ^ {2}\ +2 sombrero {\ tau}\ derecha) d\ sombrero {\ tau} =\ frac {2} {3}\\
&\ beta_ {2} =\ int_ {0} ^ {1}\ sombrero {\ phi} _ {2} (\ sombrero {\ tau}) d\ sombrero {\ tau} =\ int_ {0} ^ {1}\ frac {1}\ frac {1} {2}\ izquierda (\ sombrero {\ tau} ^ {2} -\ sombrero {\ tau}\ derecha) d\ sombrero {\ tau} =-\ frac {1} {12}
\ fin {alineado}

Así, el esquema Adams-Moulton de 2 pasos viene dado por

\(\tilde{u}^{j}=\tilde{u}^{j-1}+\Delta t\left(\frac{5}{12} g^{j}+\frac{2}{3} g^{j-1}-\frac{1}{12} g^{j-2}\right)\).

Este esquema AM2 es preciso de tercer orden.

______________________ . ______________________

Convergencia de esquemas multietapa: consistencia y estabilidad

Introduzcamos ahora técnicas para analizar la convergencia de un esquema multipaso. Debido al teorema de equivalencia de Dahlquist, solo necesitamos demostrar que el esquema es consistente y estable.

Para demostrar que el esquema es consistente, necesitamos calcular el error de truncamiento. Recordando que el error de truncamiento local se obtiene sustituyendo la solución exacta a la ecuación de diferencia (normalizada tal que\(\tilde{u}^{j}\) tiene el coeficiente de 1) y dividiendo por\(\Delta t\), tenemos para cualquier esquema de múltiples pasos

\(\tau_{\text {trunc }}^{j}=\frac{1}{\Delta t}\left[u\left(t^{j}\right)+\sum_{k=1}^{K} \alpha_{k} u\left(t^{j-k}\right)\right]-\sum_{k=0}^{K} \beta_{k} g\left(t^{j-k}, u\left(t^{j-k}\right)\right)\).

Por simplicidad, especializamos nuestro análisis a la familia Adams-Bashforth, de tal manera que

\(\tau_{\text {trunc }}^{j}=\frac{1}{\Delta t}\left(u\left(t^{j}\right)-u\left(t^{j-1}\right)\right)-\sum_{k=1}^{n} \beta_{k} g\left(t^{j-k}, u\left(t^{j-k}\right)\right)\).

Recordamos que los coeficientes\(\beta_{k}\) se seleccionaron para que coincidieran con la extrapolación a partir del ajuste polinómico. Retrocediendo la derivación, simplificamos la suma de la siguiente manera

\ begin {alineado}
\ sum_ {k=1} ^ {K}\ beta_ {k} g\ izquierda (t^ {j-k}, u\ izquierda (t^ {j-k}\ derecha)\ derecha) &=\ sum_ {k=1} ^ {K}\ int_ {0} ^ {1}\ sombrero {\ phi} _ {k} (\ hat {\ tau}) d\ sombrero {\ tau} g\ izquierda (t^ {j-k}, u\ izquierda (t^ {j-k}\ derecha)\ derecha)\\
&=\ sum_ {k=1} ^ {K}\ frac {1} {\ Delta t}\ int_ {t^ {j-1}} ^ {t^ {j}}\ phi_ {k} (\ tau ) d\ tau g\ izquierda (t^ {j-k}, u\ izquierda (t^ {j-k}\ derecha)\ derecha)\\
&=\ frac {1} {\ Delta t}\ int_ {t^ {j-1}} ^ {t^ {j}}\ izquierda [\ sum_ {k=1} ^ {K}\ phi_ {k} (\ tau) g\ izquierda (t^ ^ {j-k}, u\ izquierda (t^ {j-k}\ derecha)\ derecha)\ derecha] d\ tau\\
&=\ frac {1} {\ Delta t}\ int_ {t^ {j-1}} ^ {t^ {j}} p (\ tau) d\ tau
\ fin {alineado}

Recordamos que\(p(\tau)\) es un polinomio de\((K-1)^{\text {th }}\) grado aproximado\(g(\tau, u(\tau))\). En particular, se trata de una interpolación precisa de\(K^{\text {th }}\) orden -orden con el error\(\mathcal{O}\left(\Delta t^{K}\right)\). Por lo tanto,

\ begin {alineado}
\ tau_ {\ text {trunc}} ^ {j} &=\ frac {1} {\ Delta t}\ izquierda (u\ izquierda (t^ {j}\ derecha) -u\ izquierda (t^ {j-1}\ derecha)\ derecha) -\ suma_ {k=1} ^ {K}\ beta_ {k} g\ izquierda (t^ {j-k}, u\ izquierda (t^ {j-k}\ derecha)\ derecha)\
&=\ frac {1} {\ Delta t}\ izquierda (u\ izquierda (t^ {j}\ derecha) -u\ izquierda (t^ {j-1}\ derecha)\ derecha) -\ frac {1} {\ Delta t}\ int_ {t^ {j-1}} ^ {t^ {j}} g (\ tau, u (\ tau)) d\ tau+\ frac {1} {\ Delta t}\ int_ {j^ {j-1}} ^ {t^ {j}}\ mathcal {O}\ izquierda (\ Delta t^ {K}\ derecha) d\ tau\
&= frac {1} {\ Delta t}\ izquierda [u\ izquierda (t^ {j}\ derecha) -u\ izquierda (t^ {j-1}\ derecha) -\ int_ {t^ {j-1}} ^ {t^ {j}} g (\ tau, u (\ tau)) d\ tau\ derecha] +\ mathcal {O}\ izquierda (\ Delta t^ {K }\ derecha)\\
&=\ mathcal {O}\ izquierda (\ Delta t^ {K}\ derecha).
\ end {alineado}

Obsérvese que el término en el paréntesis se desvanece de\(g=d u / d t\) y el teorema fundamental del cálculo. El error de truncamiento del esquema es\(\mathcal{O}\left(\Delta t^{K}\right)\). En particular, ya que\(K>0\),\(\tau_{\text {trunc }} \rightarrow 0\) as\(\Delta t \rightarrow 0\) y los esquemas Adams-Bashforth son consistentes. Así, si los esquemas son estables, convergerían en\(\Delta t^{K}\).

El análisis de estabilidad se basa en una técnica de solución para ecuaciones de diferencia. Primero nos limitamos a la ecuación lineal de la forma\(g(t, u)=\lambda u\). Al reorganizar la forma de ecuación de diferencia para los métodos multipaso, obtenemos

\(\sum_{k=0}^{K}\left(\alpha_{k}-(\lambda \Delta t) \beta_{k}\right) \tilde{u}^{j-k}=0, \quad j=1, \ldots, J\)

La solución a la ecuación de diferencia se rige por la condición inicial y las\(K\) raíces del polinomio

\(q(x)=\sum_{k=0}^{K}\left(\alpha_{k}-(\lambda \Delta t) \beta_{k}\right) x^{K-k}\).

En particular, para cualquier condición inicial, la solución exhibirá un comportamiento estable si todas las raíces\(r_{k}\),\(k=1, \ldots, K\), tienen una magnitud menor o igual a la unidad. Por lo tanto, la condición de estabilidad absoluta para esquemas multietapa es

\((\lambda \Delta t)\)de tal manera que\(\left|r_{K}\right| \leq 1, \quad k=1, \ldots, K\)

donde\(r_{k}, k=1, \ldots, K\) están las raíces de\(q\).

Ejemplo 21.1.9 Estabilidad del esquema Adams-Bashforth de 2 etapas

Recordemos que el Adams-Bashforth de 2 pasos resulta de la elección

\(\alpha_{0}=1, \quad \alpha_{1}=-1, \quad \alpha_{2}=0, \quad \beta_{0}=0, \quad \beta_{1}=\frac{3}{2}, \quad \text { and } \quad \beta_{2}=-\frac{1}{2}\).

La estabilidad del esquema se rige por las raíces del polinomio

\(q(x)=\sum_{k=0}^{2}\left(\alpha_{k}-(\lambda \Delta t) \beta_{k}\right) x^{2-k}=x^{2}+\left(-1-\frac{3}{2}(\lambda \Delta t)\right) x+\frac{1}{2}(\lambda \Delta t)=0\).

Las raíces del polinomio están dadas por

\(r_{1,2}=\frac{1}{2}\left[1+\frac{3}{2}(\lambda \Delta t) \pm \sqrt{\left(1+\frac{3}{2}(\lambda \Delta t)\right)^{2}-2(\lambda \Delta t)}\right]\).

Ahora buscamos\((\lambda \Delta t)\) tal que\(\left|r_{1}\right| \leq 1\) y\(\left|r_{2}\right| \leq 1\).
Es una cuestión sencilla determinar si un particular\(\lambda \Delta t\) está dentro, en el límite de, o fuera de la región de estabilidad absoluta. Por ejemplo, para\(\lambda \Delta t=-1\) obtenemos\(r_{1}=-1, r_{2}=1 / 2\) y por lo tanto ya que de hecho\(\left|r_{1}\right|=1-\lambda \Delta t=-1\) está en el límite del diagrama de estabilidad absoluta. Del mismo modo, es sencillo confirmar que\(\lambda \Delta t=-1 / 2\) los rendimientos tanto como\(r_{1}\)\(r_{2}\) de módulo son estrictamente inferiores a 1, y por lo tanto\(\lambda \Delta t=-1 / 2\) se encuentra dentro de la región de estabilidad absoluta. Por lo tanto, en principio podemos verificar cada punto\(\lambda \Delta t\) (o contratar procedimientos de solución más sofisticados) para construir el diagrama de estabilidad absoluta completo.

Nos ocuparemos principalmente del uso del diagrama de estabilidad en lugar de la construcción del diagrama de estabilidad, que para la mayoría de los esquemas de interés ya están derivados y bien documentados. Presentamos en la Figura 21.11 (b) el diagrama de estabilidad absoluta para el esquema AdamsBashForth de 2 pasos. A modo de comparación se muestra en la Figura 21.11 (a) el diagrama de estabilidad absoluta para Euler Forward, que es el esquema Adams-Bashforth de 1 paso. Tenga en cuenta que la región de estabilidad de los esquemas Adams-Bashforth es bastante pequeña; de hecho, la región de estabilidad disminuye aún más para los esquemas Adams-Bashforth de orden superior. Por lo tanto, el método solo es adecuado para ecuaciones no rígidas.

______________________ . ______________________

Ejemplo 21.1.10 Estabilidad del esquema Crank-Nicolson

Analicemos la estabilidad absoluta del esquema Crank-Nicolson. Recordemos que la estabilidad de un esquema multipaso se rige por las raíces del polinomio

\(q(x)=\sum_{k=0}^{K}\left(\alpha_{k}-\lambda \Delta t \beta_{k}\right) x^{K-k}\).

Figura 21.11: Los diagramas de estabilidad para los métodos de Adams-Bashforth.

Para el esquema de Crank-Nicolson, tenemos\(\alpha_{0}=1, \alpha_{1}=-1, \beta_{0}=1 / 2\), y\(\beta_{1}=1 / 2\). Así, el polinomio es

\(q(x)=\left(1-\frac{1}{2}(\lambda \Delta t)\right) x+\left(-1-\frac{1}{2}(\lambda \Delta t)\right)\).

La raíz del polinomio es

\(r=\frac{2+(\lambda \Delta t)}{2-(\lambda \Delta t)}\).

Para resolver el límite de estabilidad, establezcamos\(|r|=1=\left|e^{i \theta}\right|\) y resolvamos para\((\lambda \Delta t)\), i.e.

\(\frac{2+(\lambda \Delta t)}{2-(\lambda \Delta t)}=e^{i \theta} \quad \Rightarrow \quad(\lambda \Delta t)=\frac{2\left(e^{i \theta}-1\right)}{e^{i \theta}+1}=\frac{i 2 \sin (\theta)}{1+\cos (\theta)}\).

Así, como\(\theta\) varía de 0 a\(\pi / 2, \lambda \Delta t\) varía de 0 a\(i \infty\) lo largo del eje imaginario. Del mismo modo, como\(\theta\) varía de 0 a\(-\pi / 2, \lambda \Delta t\) varía de 0 a\(-i \infty\) lo largo del eje imaginario. Así, el límite de estabilidad es el eje imaginario. La región de estabilidad absoluta es todo el plano izquierdo (complejo).

Los diagramas de estabilidad para los métodos Adams-Moulton de 1 y 2 etapas se muestran en la Figura 21.11. El esquema Crank-Nicolson muestra el diagrama de estabilidad ideal; es estable para todas las ODE estables\((\lambda \leq 0)\) e inestable para todas las ODE inestables\((\lambda>0)\) independientemente de la selección de paso de tiempo. (Además, para las ODE neutralmente estables\(\lambda=0\), Crank-Nicolson es neutralmente estable\(-\gamma\), el factor de amplificación, es la unidad). La selección del paso de tiempo viene dictada por el requisito de precisión en lugar de preocupaciones de estabilidad. \(^{1}\)A pesar de ser un esquema implícito, AM2 no es estable para todos\(\lambda \Delta t\) en el plano izquierdo; por ejemplo, a lo largo del eje real, el paso de tiempo está limitado a\(-\lambda \Delta t \leq 6\). Si bien la región de estabilidad es mayor que, por ejemplo, el esquema Euler Forward, la región de estabilidad de AM2 es bastante decepcionante considerando el costo computacional adicional asociado a cada paso de un esquema implícito.

______________________ . ______________________

Figura 21.12: Los diagramas de estabilidad para los métodos Adams-Moulton en 2 etapas.

Fórmulas de diferenciación inversa

Las fórmulas de diferenciación hacia atrás son esquemas implícitos de múltiples pasos que son muy adecuados para problemas rígidos. A diferencia de los esquemas Adams-Bashforth y Adams-Moulton, nos limitamos a

\(\beta_k = 0, k = 1,...,K\).

Así, las Fórmulas Diferenciales Atrás son de la forma

\(\tilde{u}^{j}+\sum_{k=1}^{K} \alpha_{k} \tilde{u}^{j-k}=\Delta t \beta_{0} g^{j}\).

Nuestra tarea es encontrar los coeficientes\(\alpha_{k}, k=1, \ldots, K\), y\(\beta_{0}\). Primero construimos un polinomio interpolante de\(K^{\text {th }}\) grado usando\(\tilde{u}^{j-k}, k=0, \ldots, K\), para aproximar\(u(t)\), i.e.

\(u(t) \approx \sum_{k=0}^{K} \phi_{k}(t) \tilde{u}^{j-k}\)

donde\(\phi_{k}(t), k=0, \ldots, K\), son los polinomios de interpolación de Lagrange definidos en los puntos\(t^{j-k}\),\(k=0, \ldots, K\) es decir, los mismos polinomios utilizados para desarrollar los esquemas Adams-Moulton. Diferenciando la función y evaluándola en\(t=t^{j}\), obtenemos

\(\left.\left.\frac{d u}{d t}\right|_{t^{j}} \approx \sum_{k=0}^{K} \frac{d \phi_{k}}{d t}\right|_{t^{j}} \tilde{u}^{j-k}\).

Nuevamente, aplicamos el cambio de variable de la forma\(t=t^{j}-\Delta t \hat{\tau}\), de manera que

\(\left.\left.\left.\frac{d u}{d t}\right|_{t^{j}} \approx \sum_{k=0}^{K} \frac{d \hat{\phi}_{k}}{d \hat{\tau}}\right|_{0} \frac{d \hat{\tau}}{d t}\right|_{t^{j}} \tilde{u}^{j-k}=-\left.\frac{1}{\Delta t} \sum_{k=0}^{K} \frac{d \hat{\phi}_{k}}{d \hat{\tau}}\right|_{0} \tilde{u}^{j-k}\).

Recordando\(g^{j}=g\left(u\left(t^{j}\right), t^{j}\right)=d u /\left.d t\right|_{t^{j}}\), establecemos

\(\tilde{u}^{j}+\sum_{k=1}^{K} \alpha_{k} \tilde{u}^{j-k} \approx \Delta t \beta_{0}\left(-\left.\frac{1}{\Delta t} \sum_{k=0}^{K} \frac{d \hat{\phi}_{k}}{d \hat{\tau}}\right|_{0} \tilde{u}^{j-k}\right)=-\left.\beta_{0} \sum_{k=0}^{K} \frac{d \hat{\phi}_{k}}{d \hat{\tau}}\right|_{0} \tilde{u}^{j-k}\).

Coincidiendo con los coeficientes para\(\tilde{u}^{j-k}, k=0, \ldots, K\), obtenemos

\ begin {aligned}
1 &=-\ left. \ beta_ {0}\ frac {d\ hat {\ phi} _ {k}} {d\ hat {\ tau}}\ derecha|_ {0}\\
\ alpha_ {k} &=-\ izquierda. \ beta_ {0}\ frac {d\ hat {\ phi} _ {k}} {d\ hat {\ tau}}\ derecha|_ {0},\ quad k=1,\ ldots, K.
\ end {alineado}

Desarrollemos algunas Fórmulas de Diferenciación hacia Atrás.

Ejemplo 21.1.11 Fórmula de diferenciación hacia atrás de 1 paso (Euler hacia atrás)

La fórmula de diferenciación hacia atrás de 1 paso requiere la especificación de\(\beta_{0}\) y\(\alpha_{1}\). Al igual que en el esquema Adams-Moulton de 1 paso, los polinomios de Lagrange para este caso son

\(\hat{\phi}_{0}(\hat{\tau})=-\tau+1 \quad \text { and } \quad \hat{\phi}_{1}(\hat{\tau})=\tau\).

Diferenciar y evaluar en\(\hat{\tau}=0\)

\ begin {alineado}
&\ beta_ {0} =-\ left (\ left. \ frac {d\ hat {\ phi} _ {0}} {d\ hat {\ tau}}\ derecha|_ {0}\ derecha) ^ {-1} =- (-1)\\
&\ alpha_ {1} =-\ izquierda. \ beta_ {0}\ frac {d\ hat {\ phi} _ {1}} {d\ hat {\ tau}}\ derecha|_ {0} =-1
\ end {alineado}

El esquema resultante es

\(\tilde{u}^{j}-\tilde{u}^{j-1}=\Delta t g^{j}\)

que es el esquema de Euler Atrás. Otra vez.

______________________ . ______________________

Ejemplo 21.1.12 Fórmula de diferenciación hacia atrás de 2 pasos

La fórmula de diferenciación hacia atrás de 2 pasos requiere la especificación de\(\beta_{0}, \alpha_{1}\), y\(\alpha_{2}\). Los polinomios de Lagrange para este caso son

\ begin {alineado}
&\ hat {\ phi} _ {0} (\ hat {\ tau}) =\ frac {1} {2}\ izquierda (\ hat {\ tau} ^ {2} -3\ sombrero {\ tau} +2\ derecha),\\
&\ hat {\ phi} _ {1} (\ hat {\ tau}) =-\ hat {\ tau} ^ {2} +2\ sombrero {\ tau},\\
&\ sombrero {\ phi} _ {2} (\ sombrero {\ tau}) =\ frac {1} {2}\ izquierda (\ sombrero {\ tau} ^ {2} -\ sombrero {\ tau}\ derecha).
\ end {alineado}

Rendimientos de diferenciación

\(\beta_{0}=-\left(\left.\frac{d \hat{\phi}_{0}}{d \hat{\dagger}}\right|_{0}\right)^{-1}=\frac{2}{3}\),

\ begin {alineado}
&\ alpha_ {1} =-\ left. \ beta_ {0}\ frac {d\ sombrero {\ phi_ {1}}} {d\ sombrero {\ gamma}}\ derecha|_ {0} =-\ frac {2} {3}\ cdot 2=-\ frac {4} {3},\\
&\ alpha_ {2} =-\ izquierda. \ beta_ {0}\ frac {d\ sombrero {\ phi} _ {2}} {d\ sombrero {\ gamma}}\ derecha|_ {0} =-\ frac {2} {3}\ cdot-\ frac {1} {2} =\ frac {1} {3}.
\ end {alineado}

Figura 21.13: Los diagramas de estabilidad absoluta para las fórmulas de diferenciación hacia atrás.

El esquema resultante es

\(\vec{u}^{j}-\frac{4}{3} \hat{w}^{j-1}+\frac{1}{3} \hat{w}^{j-2}=\frac{2}{3} \Delta t g^{j}\).

La fórmula de diferenciación hacia atrás de 2 pasos (BDF2) es incondicionalmente estable y precisa de segundo orden.

______________________ . ______________________

Ejemplo 21.1.13 Fórmula de diferenciación hacia atrás de 3 pasos

Siguiendo el mismo procedimiento, podemos desarrollar la fórmula de diferenciación hacia atrás de 3 pasos (BDF3). El esquema viene dado por

\(\tilde{u}^{j}-\frac{18}{11} \tilde{w}^{j-1}+\frac{9}{11} \tilde{w}^{j-2}-\frac{2}{11} \tilde{u}^{j-3}=\frac{6}{11} \Delta t g^{j}\).

El esquema es incondicionalmente estable y es de tercer ozder preciso.

______________________ . ______________________

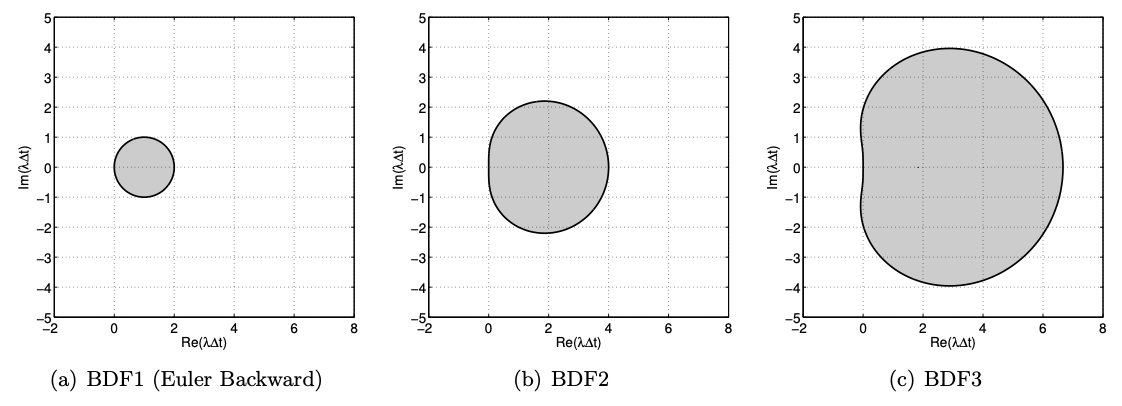
Los diagramas de estabilidad para las fórmulas de diferenciación hacia atrás de 1, 2 y 3 pasos se muestran en la Figura 21.13. Los esquemas BDF1 y BDF2 son estables A (es decir, la región estable incluye todo el plano izquierdo). Desafortunadamente, BDF3 no es $A $-estable; de hecho la región de inestabilidad en los valores propios se agrupa a lo largo del eje real, los métodos BDF son opciones atractivas.

Esquemas multietapa: Runge-Kutta

Otra familia de esquemas de integración importantes y poderosos son los esquemas multietapa, los más famosos de los cuales son los esquemas Runge-Kutta. Mientras que un análisis detallado del Runge-Kutta y el contexto de ingeniería.

A diferencia de los esquemas multietapa, los esquemas multietapa solo requieren la solución en el paso de tiempo anterior\(\tilde{u}^{j-1}\) para aproximarse al nuevo estado\(\tilde{u}^{j}\) en el momento\(t^{j}\). Para desarrollar una fórmula de actualización, primero observamos que

\(u\left(t^{j}\right)=\tilde{u}\left(t^{j-1}\right)+\int_{t^{j-1}}^{j^{j}} \frac{d u}{d t}(\tau) d \tau=\tilde{u}\left(t^{j-1}\right)+\int_{t-1}^{t^{j}} g(u(\tau), \tau) d \tau\).

Claramente, no podemos usar la fórmula directamente para aproximarnos\(u\left(t^{j}\right)\) porque no sabemos\(g(u(\tau), \tau)\),\(\tau \in t^{j-1}, l[\). Para derivar los esquemas Adams, reemplazamos la función desconocida\(g\) con su polinomio aplicar directamente cuadratura numérica a la integral para obtener

\(u\left(t^{j}\right) \approx u\left(t^{j-1}\right)+\Delta t \sum_{k=1}^{K} b_{k} g\left(u\left(t^{j-1}+c_{k} \Delta t\right), t^{j-1}+c_{k} \Delta t\right)\),

donde\(b_{k}\) están los pesos de cuadratura y los\(t^{j}+c_{k} \Delta t\) son los puntos de cuadratura. Necesitamos hacer más aproximaciones para definir un esquema, porque desconocemos los valores de\(u\) en las\(K\) etapas,\(u\left(t^{j}+c_{k} \Delta t\right), k=1, \ldots, K\). Nuestro enfoque es reemplazar el por aproximaciones\(v_{k}\) y luego formar las derivadas de la\(K\) etapa como

\(G_{k}=g\left(v_{k}, t^{j-1}+c_{k} \Delta t\right)\).

Queda por precisar el esquema de aproximación.

Para un esquema explícito de Runge-Kutta, construimos la\(k^{\text {th-stage approximation as a linear }}\) combinación de las derivadas de la etapa anterior y\(\tilde{\omega}^{j-1}\), i.e.

\(v_{k}=\tilde{u}^{j-1}+\Delta t\left(A_{k 1} G_{1}+A_{k 2} G_{2}+\cdots+A_{k, k-1} G_{k-1}\right)\)

Debido a que esta\(k^{\text {th-stage }}\) estimación solo depende de las derivadas de la etapa anterior, podemos calcular los valores de etapa en secuencia,

\ begin {array} {ll}
v_ {1} =\ tilde {u} ^ {j-1} &\ izquierda (\ fila derecha G_ {1}\ derecha),\\
v_ {2} =\ tilde {u} ^ {j-1} +\ Delta t A_ {21} G_ {1} &\ izquierda (\ fila derecha G_ {2}\ derecha),\\
v_ {3} =\ tilde {u} ^ {j-1} +\ Delta t A_ {31} G_ {1} +\ Delta t A_ {32} G_ {2} &\ izquierda (\ fila derecha G_ {3}\ derecha), \\
v_ {K} =\ tilde {u} ^ {j-1} +\ Delta t\ suma_ {k=1} ^ {K-1} A_ {K k} G_ {k} &\ izquierda (\ fila derecha G_ {K}\ derecha)
\ end {array}

Una vez que los valores de etapa están disponibles, estimamos la integral por

\(\tilde{u}^{j}=\tilde{u}^{j-1}+\Delta t \sum_{k=1}^{K} b_{k} G_{k}\),

y proceder al siguiente paso de tiempo.

Tenga en cuenta que un esquema de Runge-Kutta se define de manera única por la elección del vector\(b\) para el peso en cuadratura, el vector\(e\) para los puntos de cuadratura y la matriz\(A\) para la reconstrucción de la etapa. La forma

\(c\)	\(A\)
\ (c\) ">	\ (A\) ">\(b^{\mathrm{T}}\)

Para los métodos explícitos de Runge-Kutta, requerimos\(A_{i j}=0, i \leq j\). Presentemos ahora dos esquemas populares explícitos de Runge-Kutta.

Ejemplo 21.1.14 Runge-Kutta de dos etapas

Un popular método Runge-Kutta de dos etapas (RK2) tiene la mesa Carnicero

\ begin {array} {l|ll}
0 & &\\
\ frac {1} {2} &\ frac {1} {2} &\
\ hline & 0 & 1
\ end {array}

Esto da como resultado la siguiente fórmula de actualización

\ begin {array} {ll}
v_ {1} =\ tilde {w} ^ {j-1}, & G_ {1} =g\ izquierda (v_ {1}, t^ {j-1}\ derecha),\\
v_ {2} =\ tilde {w} ^ {j-1} +\ frac {1} {2}\ Delta t G_ {1}, & G_ {2} =g\ izquierda (v_ {2}, t^ {j-1} +\ frac {1} {2}\ Delta t\ derecha),\\
\ tilde {u} ^ {j} =\ tilde {w} ^ {j} +\ Delta t G_ {2}. &
\ end {matriz}

El esquema Runge-Kutta de dos etapas es conditsonalmente estable y es preciso de segundo orden. Podríamos ver este esquema como una especie de regla de punto medio.

______________________ . ______________________

Ejemplo 21.1.15 Runge-Kutta de cuatro etapas

Un método popular de cuatro etapas Runge-Kutta (RK4) -y quizás el más popular de todos los métodos RungeKutta- tiene la mesa Carnicero de la forma

\ begin {array} {l|llll}
0 & & & & &
\\ frac {1} {2} &\ frac {1} {2} & & & &
\\ frac {1} {2} & 0 &\ frac {1} {2} & &\
1 & 0 & 0 &\
\ hline &\ frac {1} {6} &\ frac {1} {3} & \ frac {1} {3} &\ frac {1} {6}
\ end {array}

Esto da como resultado la siguiente fórmula de actualización

\ begin {array} {ll}
v_ {1} =\ tilde {u} ^ {j-1}, & G_ {1} =g\ izquierda (v_ {1}, t^ {j-1}\ derecha),\\
v_ {2} =\ tilde {u} ^ {j-1} +\ frac {1} {2}\ Delta t G_ {1}, & G_ {2} =g\ izquierda (v_ {2}, t^ {j-1} +\ frac {1} {2}\ Delta t\ derecha)\\
v_ {3} =\ tilde {u} ^ {j-1} +\ frac {1} {2}\ Delta t G_ {2}, & G_ {3} =g\ izquierda (v_ {3}, t^ {-1} +\ frac {1} {2}\ Delta t\ derecha)\\
v_ {4} =\ tilde {u} ^ {j-1} +\ Delta t G_ {3}, & G_ {4} =g\ izquierda (v_ {4}, j^ {j-1} +\ Delta t\ derecha),\
\\ tilde u} ^ {j} =\ tilde {u} ^ {j-1} +\ Delta t\ izquierda (\ frac {1} {6} G_ {1} +\ frac {1} {3} G_ {2} +\ frac {1} {3} G_ {3} +\ frac {1} {6} G_ {4}\ derecha).
\ end {matriz}

El esquema de cuatro etapas de Runge-Kutta es condicionalmente estable y es de cuarto orden exacto.

______________________ . ______________________

El análisis de precisión de los esquemas Runge-Kutta es bastante complicado y se omite aquí. También vale la pena señalar que aunque podemos lograr una precisión de cuarto orden usando un método Runge-Kutta de cuatro etapas, son necesarias seis etapas para lograr una precisión de quinto orden.

Los métodos explícitos de Runge-Kutta requerían que un valor de etapa sea una combinación lineal de las derivadas de la etapa anterior. En otras palabras, la\(A\) matriz es triangular inferior con ceros en la diagonal. Esto hizo que el cálculo de los valores de estado fuera sencillo, ya que podríamos calcular los valores de etapa en secuencia. Si eliminamos esta restricción, llegamos a la familia de métodos implícitos de Runge-Kutta (IRK). Las actualizaciones del valor de etapa para los esquemas implícitos de Runge-Kutta están completamente acopladas, i.e.

\(v_{k}=\tilde{u}^{j-1}+\Delta t \sum_{i=1}^{K} A_{k\}} G_{i}, \quad k=1, \ldots, K\)

Es decir, la matriz\(A\) está llena en general. Al igual que otros métodos implícitos, los esquemas implícitos de Runge-Kutta tienden a ser estables a la mota que sus contrapartes explícitas (aunque también más caros por paso de tiempo). Además, para todos\(K\), existe un método IRK único que logra un\(2K\) orden de precisión. Introducimos uno de esos esquemas.

Ejemplo 21.1.16 Gauss-Legendre de dos etapas Runge-Kutta implícita

El método de dos etapas Gauss-Legendre Runge-Kutta (GL-IRK2) es descrito por la mesa Butcher

\ begin {array} {c|cc}
\ frac {1} {2} -\ frac {\ sqrt {3}} {6} &\ frac {1} {4} &\ frac {1} {4} -\ frac {\ sqrt {3}} {6}\
\ frac {1} {2} +\ frac {\ sqrt {3}} {6} &\ frac {1} {4} +\ frac {\ sqrt {3}} {6} &\ frac {1} {4}\
\ hline &\ frac {1} {2} &\ frac {1} {2}
\ end {array}.

Para calcular la actualización primero debemos resolver un sistema de ecuaciones para obtener los valores de etapa\(v_1\) y\(v_2\)

\(v_{1}=\tilde{u}^{j-1}+A_{11} \Delta t G_{1}+A_{12} \Delta G_{2}\)

\(v_{2}=\tilde{u}^{j-1}+A_{21} \Delta t G_{1}+A_{12} \Delta G_{2}\)

o

\(v_{1}=\tilde{u}^{j-1}+A_{11} \Delta t g\left(v_{1}, t^{j-1}+c_{1} \Delta t\right)+A_{12} \Delta t g\left(v_{2}, t^{j-1}+c_{2} \Delta t\right)\),

\(v_{2}=\tilde{u}^{j-1}+A_{21} \Delta t g\left(v_{1}, t^{j-1}+c_{1} \Delta t\right)+A_{22} \Delta t g\left(v_{2}, t^{j-1}+c_{2} \Delta t\right)\)

donde los coeficientes\(A\) y\(c\) son proporcionados por la mesa Carnicero. Una vez calculados los valores de etapa, calculamos de\(\tilde{u}^{j}\) acuerdo con

\(\tilde{w}^{j}=\bar{u}^{j-1}+\Delta t\left(b_{1} g\left(v_{1}, t^{j-1}+c_{1} \Delta t\right)+b_{2} g\left(v_{2}, t^{j-1}+c_{2} \Delta t\right)\right)\),

donde los coeficientes\(b\) son dados por la mesa Carnicero.

El esquema de dos etapas de Gauss-Legendre Runge-Kutta es\(A\) -estable y es de cuarto orden exacto. Si bien el método es computacionalmente costoso y difícil de implementar, la estabilidad A y la precisión de cuarto orden son características atractivas para ciertas aplicaciones.

Figura 21.14: Los diagramas de estabilidad absoluta para la familia de esquemas Runge-Kutta.

______________________ . ______________________

Existe una familia de métodos implícitos de Runge-Kutta llamados diagonalmente imphicit Rtunge-Kutto (DIRK). Estos métodos tienen una\(A\) matriz que es triangular inferior con los mismos coeficientes en cada elemento diagonal. Esta familia de métodos hereda la ventaja de estabilidad del esquema IIK puede actualizar incrementalmente las etapas.

Los diagramas de estabilidad para los tres esquemas de Runge-Kutta presentados se muestran en la Figura $21.14$. Los dos métodos explícitos de Runge-Kutta, RK2 y RK4, no son estables a $ A $. El paso de tiempo a lo largo del eje real se limita a $-\ lambda\ Delta t\ leq 2$ para RK2 y $-\ lambda\ Delta t\ lesssim 2.8$ para RK4. Sin embargo, la región de estabilidad para los esquemas explícitos de Runge-Kutta es considerablemente mayor que la familia Adams-Bashforth de esquemas explícitos. Si bien los métodos explícitos de Runge-Kutta no son adecuados para sistemas muy rígidos, se pueden usar para sistemas moderadamente rígidos. Lo implícito exhibe
correctamente un comportamiento de crecimiento para sistemas inestables.

La Figura 21.15 muestra el comportamiento de error de los esquemas Runge-Kutta aplicados a\(du/dt = −4u\). La mayor precisión de los esquemas Runge-Kutta en comparación con el esquema Euler Forward es evidente a partir de la solución. La gráfica de convergencia de error confirma las tasas de convergencia teóricas para estos métodos.