27.5: El inverso malvado

Al resolver un sistema lineal\(A u=f\), abogamos por una estrategia de dos pasos que consiste en la eliminación gaussiana y la sustitución inversa, es decir,\[\begin{aligned} \text { Gaussian elimination: } & A u=f \quad \Rightarrow \quad U u=\hat{f} \\ \text { Back substitution: } & U u=\hat{f} \quad \Rightarrow \quad u . \end{aligned}\] alternativamente, podríamos encontrar\(u\) formando explícitamente la inversa de\(A, A^{-1}\). Recordemos que si\(A\) es no singular (como lo indican, por ejemplo, columnas independientes), existe una matriz única\(A^{-1}\) tal que\[A A^{-1}=I \text { and } A^{-1} A=I .\] La matriz inversa\(A^{-1}\) es relevante para los sistemas de solución porque, en principio, podríamos

1. Construir\(A^{-1}\);
2. Evaluar\(u=A^{-1} f\) (es decir, producto matriz-vector).

Obsérvese que el segundo paso se deriva del hecho de que\[\begin{aligned} A u &=f \\ A^{-1} A u &=A^{-1} f \\ I u &=A^{-1} f . \end{aligned}\] Si bien el procedimiento es matemáticamente válido, advertimos que un sistema lineal nunca debe resolverse formando explícitamente la inversa.

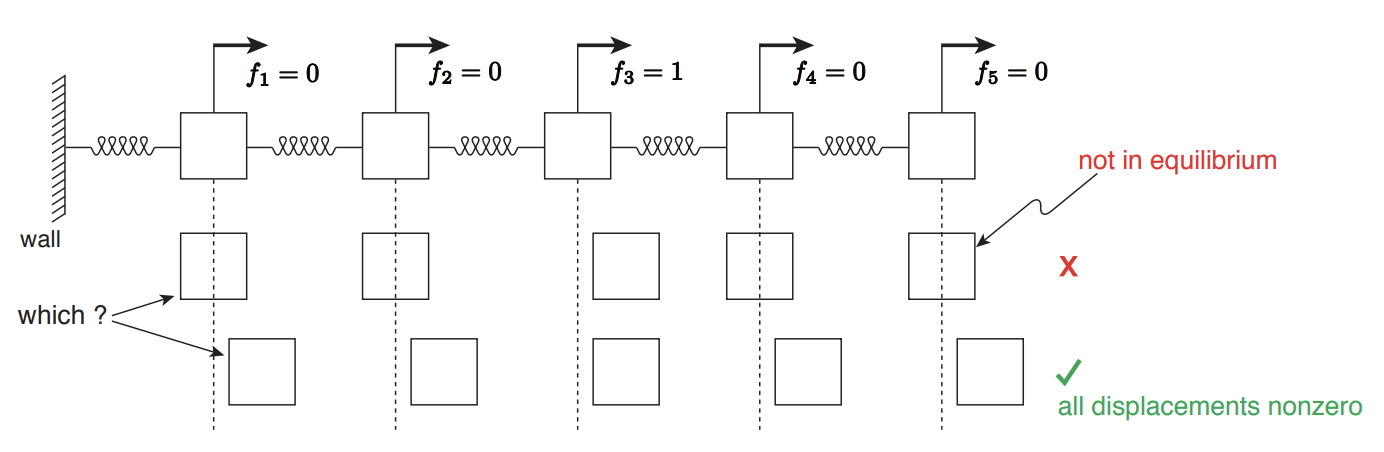
Para motivar por qué se debe evitar explícitamente la construcción de matrices inversas, estudiemos el patrón de dispersidad de la matriz inversa para un sistema de masa de resorte\(n\) -masa, ejemplo del cual\(n=5\) se muestra en la Figura\(27.8\). Utilizamos la interpretación de columna de la matriz y asociamos la columna\(j\) de\(A^{-1}\) con un vector\(p^{j}\), i.e.

Figura 27.8: Respuesta de un sistema de\(n=5\) resorte-masa a la carga unitaria sobre la masa 3.

Desde\(A u=f\) y\(u=A^{-1} f\), tenemos (usando un producto matriz-vector de una mano),

A partir de esta expresión, queda claro que el vector\(p^{j}\) es igual a los desplazamientos de masas debido a la fuerza unitaria que actúa sobre la masa\(j\). En particular la\(i^{\text {th }}\) entrada de\(p^{j}\) es el desplazamiento de la\(i^{\text {th }}\) masa debido a la fuerza unitaria sobre la\(j^{\text {th }}\) masa.

Ahora, para deducir el patrón distinto de cero de un vector\(p^{j}\), centrémonos en el caso que se muestra en la Figura\(27.8\); deduciremos las entradas distintas de cero de\(p^{3}\) para el\(n=5\) sistema. Consideremos una secuencia de eventos que tiene lugar cuando\(f_{3}\) se aplica (nos centramos en el resultado cualitativo más que en el resultado cuantitativo, es decir, si las masas se mueven, no en cuánto):

1. La masa 3 se mueve hacia la derecha debido a la carga de la unidad\(f_{3}\).
2. La fuerza ejercida por la masa de conexión de resorte 3 y 4 aumenta a medida que disminuye la distancia entre la masa 3 y 4.
3. La masa 4 ya no está en equilibrio ya que hay una fuerza mayor desde la izquierda que desde la derecha (es decir, de la masa de conexión del resorte 3 y 4, que ahora está comprimida, que de la masa de conexión del resorte 4 y 5, que es neutra). 4. Debido a la fuerza desequilibrada, la masa 4 se mueve hacia la derecha.
4. El movimiento de la masa 4 hacia la izquierda desencadena una secuencia de eventos que mueve la masa 5, así como el movimiento de la masa 3 desplazó a la masa 4. A saber, la fuerza sobre la masa 4 y 5 de conexión del resorte aumenta, la masa 5 ya no está en equilibrio y la masa 5 se mueve hacia la derecha.

De esta manera, es evidente que la carga unitaria sobre la masa 3 no sólo mueve la masa 3 sino también la masa 4 y 5 en la Figura\(27.8\). Usando el mismo argumento cualitativo, podemos convencernos de que la masa 1 y 2 también deben moverse cuando la masa 3 es desplazada por la unidad de carga. Así, en general, la carga unitaria\(f_{3}\) sobre la masa 3 da como resultado el desplazamiento de todas las masas del sistema. Recordando que la\(i^{\text {th }}\) entrada de\(p^{3}\) es el desplazamiento de la\(i^{\text {th }}\) masa debido a la carga unitaria\(f_{3}\), concluimos que todas las entradas de\(p^{3}\) son distintas de cero. (En ausencia de amortiguación, el sistema excitado por la carga unitaria oscilaría y nunca llegaría a descansar; en un sistema real, la amortiguación intrínseca presente en los resortes lleva al sistema a un nuevo estado de equilibrio).

La generalización del argumento anterior a un sistema\(n\) -mass es sencilla. Además, usando el mismo argumento, concluimos que forzar a cualquiera de las masas da como resultado el desplazamiento de todas las masas. En consecuencia\(p^{1}, \ldots, p^{n}\), para, tenemos

Recordando que\(p^{j}\) es la\(j^{\text {th }}\) columna de\(A^{-1}\), concluimos que\[A^{-1}=\left(\begin{array}{llll} & & & \\ p^{1} & p^{2} & \cdots & p^{n} \end{array}\right)\] está lleno aunque (aquí)\(A\) es tridiagonal. En general\(A^{-1}\) no preserva la escaseza de\(A\) y de hecho suele estar lleno. Esto es diferente a la matriz triangular superior resultante de la eliminación gaussiana, que conserva una gran cantidad de ceros (módulo los rellenos).

La figura\(27.9\) muestra la matriz del sistema y su inversa para el sistema\(n=10\) resorte-masa. Los colores representan el valor de cada entrada; por ejemplo, la\(A\) matriz tiene el\(\left[\begin{array}{ccc}-1 & 2 & -1\end{array}\right]\) patrón típico, a excepción de la primera y la última ecuaciones. Tenga en cuenta que la matriz inversa no es escasa y de hecho está llena. Además, los valores de cada columna de\(A^{-1}\) concuerdan con nuestra intuición física sobre los desplazamientos a una carga unitaria. Por ejemplo, cuando se aplica una carga unitaria a la masa 3, la distancia entre la pared y la masa 1 aumenta en 1 unidad, la distancia entre la masa 1 y 2 aumenta en 1 unidad, y la distancia entre la masa 3 y 2 aumenta en 1 unidad; las distancias entre las masas restantes se ven inalteradas porque no hay fuerza que actúa sobre el sistema restante en equilibrio (porque nuestro sistema no está sujeto en el extremo derecho). Acumulando desplazamientos comenzando con la masa 1, concluimos que la masa 1 se mueve por 1, la masa 2 se mueve por 2 (la suma de las distancias aumentadas entre la masa 1 y 2 y la masa 2 y 3), la masa 3 se mueve por 3 y todas las masas restantes se mueven en 3. Esta es exactamente la información contenida en la tercera columna de\(A^{-1}\), que dice\(\left[\begin{array}{llllll}1 & 2 & 3 & 3 & \ldots & 3\end{array}\right]^{\mathrm{T}}\).

Al concluir la sección, analicemos el recuento de operaciones para resolver un sistema lineal mediante la formación explícita de la inversa y la realización de multiplicación matriz-vector. Suponemos que nuestra\(n \times n\) matriz\(A\) tiene un ancho de banda de\(m_{\mathrm{b}}\). Primero, construimos la matriz inversa una columna a la vez\[\begin{aligned} & u\left[\text { for } f=\left(\begin{array}{llll}1 & 0 & \cdots & 0\end{array}\right)^{\mathrm{T}}\right]=p^{1} \leftarrow \text { nonzero in all entries! } \\ & u\left[\text { for } f=\left(\begin{array}{llll}0 & 1 & \cdots & 0\end{array}\right)^{\mathrm{T}}\right]=p^{2} \leftarrow \text { nonzero in all entries! } \\ & u\left[\text { for } f=\left(\begin{array}{llll}0 & 0 & \cdots & 0\end{array}\right)^{\mathrm{T}}\right]=p^{n} \leftarrow \text { nonzero in all entries! } \end{aligned}\]

(a)\(A\)

b)\(A^{-1}\)

Figura 27.9: Matriz\(A\) para el sistema\(n=10\) resorte-masa y su inversa\(A^{-1}\). Los colores representan el valor de cada entrada según lo especificado por la barra de colores.

resolviendo los desplazamientos de equilibrio asociados con la carga unitaria en cada masa. Para ello, primero calculamos la factorización de LU\(A\) y luego repetimos la sustitución hacia adelante y hacia atrás. Recordando el conteo de operaciones para una sola sustitución hacia adelante/atrás es\(\mathcal{O}\left(n m_{\mathrm{b}}^{2}\right)\), la construcción de\(A^{-1}\) requiere\[\begin{aligned} A p^{1}=&\left(\begin{array}{c} 1 \\ 0 \\ \vdots \\ 0 \end{array}\right) \Rightarrow p^{1} \quad \mathcal{O}\left(n m_{\mathrm{b}}^{2}\right) \mathrm{FLOPs} \\ & \vdots \\ A p^{n} &=\left(\begin{array}{c} 0 \\ 0 \\ \vdots \\ 1 \end{array}\right) \Rightarrow p^{n} \quad \mathcal{O}\left(n m_{\mathrm{b}}^{2}\right) \mathrm{FLOPs} \end{aligned}\] para el trabajo total de\(n \cdot \mathcal{O}\left(n m_{\mathrm{b}}^{2}\right) \sim \mathcal{O}\left(n^{2} m_{\mathrm{b}}^{2}\right)\) FLOP. Una vez que formamos la matriz inversa, podemos resolver el desplazamiento realizando multiplicación matriz-vector (densa), es decir,\[\left(\begin{array}{c} u_{1} \\ u_{2} \\ \vdots \\ u_{n} \end{array}\right)=\left(\begin{array}{cccc} \times & x & \cdots & \times \\ \times & \times & \cdots & \times \\ \vdots & \vdots & \ddots & \vdots \\ \times & \times & \cdots & \times \\ A^{-1} & (\text { full }) & \mathcal{O}(n \cdot n)=\mathcal{O}\left(n^{2}\right) \mathrm{FLOPs} \\ f_{n} \end{array}\right) \quad \text { one-handed or two-handed }\] tanto la construcción de la matriz inversa como la multiplicación matriz-vector requieren\(\mathcal{O}\left(n^{2}\right)\) operaciones. En contraste, recordemos que la eliminación gaussiana y la sustitución inversa resuelve un sistema lineal disperso en\(\mathcal{O}(n)\) las operaciones. Por lo tanto, un gran sistema lineal disperso nunca debe resolverse formando explícitamente su inverso.