11.1: Curva de endurecimiento y curva de rendimiento

Última actualización
Guardar como PDF

Page ID: 85186

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Si vamos al laboratorio y realizamos una prueba de tracción estándar en un espécimen redondo o un espécimen plano de hueso de perro hecho de acero o aluminio, lo más probable es que la curva de esfuerzo-deformación de ingeniería se vea como la que se muestra en la Figura (\(\PageIndex{1a}\)). Se pueden distinguir las siguientes características:

Punto A - Límite de proporcionalidad

Punto B - 0.02% de rendimiento

Punto C - punto arbitrario en la curva de endurecimiento que muestra diferentes trayectorias en la carga/descarga

Punto D - espécimen completamente descargado

Para la mayor parte del material, la porción inicial de la curva tensión-deformación es recta hasta el límite de proporcionalidad, punto A. A partir de esta etapa, la curva tensión-deformación se vuelve ligeramente curvada pero no hay un límite de elasticidad distinto con un cambio repentino de pendiente. Existe en estándar internacional el límite elástico se mapea tomando pendiente elástica con 0.02% de deformación\((\epsilon = 0.0002)\) compensada de deformación.

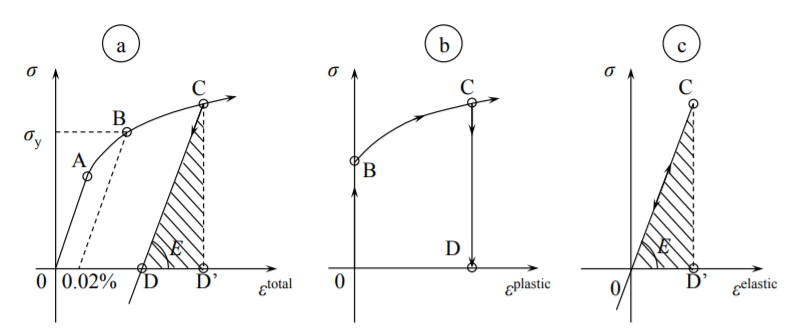
11.1.1.png — Figura\(\PageIndex{1}\): Curva elástica, plástica y tensión-deformación total.

Al cargar, el material se endurece y la tensión aumenta con la pendiente decreciente hasta que se detiene la máquina de prueba (ya sea por fuerza o desplazamiento controlado). Hay dos posibilidades. Al descargar, es decir, invertir la carga o desplazamiento de la carga cruzada de la máquina de prueba, la trayectoria de descarga es recta. Esta es la descarga elástica donde la pendiente de la curva tensión-deformación es igual a la pendiente inicial, dada por el módulo de Young. En el punto D la tensión es cero pero hay una deformación plástica residual de la magnitud OD. El experimento de carga/descarga nos dice que la deformación total\(\epsilon^{\text{total}}\) puede considerarse como la suma de la tensión plástica\(\epsilon^{\text{plastic}}\) y la tensión elástica\(\epsilon^{\text{elastic}}\). Así

\[\epsilon^{\text{total}} = \epsilon^{\text{plastic}} + \epsilon^{\text{elastic}}\]

El componente elástico no es constante sino que depende de la tensión actual

\[\epsilon^{\text{elastic}} = \frac{\sigma}{E} \]

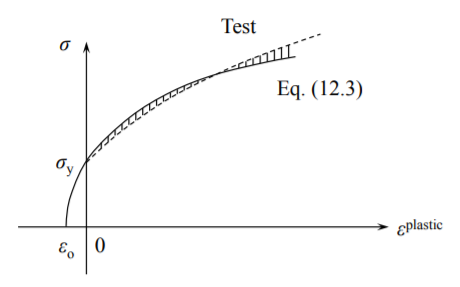
La deformación plástica depende de hasta qué punto se carga un espécimen dado, y por lo tanto hay una diferencia entre la deformación total (medida) y la deformación elástica conocida. Se sugirieron diversas fórmulas empíricas en la literatura para ajustar la relación medida entre la tensión y la deformación plástica. La más común es la ley de endurecimiento rápido

\[\sigma = A(\epsilon^{\text{plastic}} + \epsilon_o)^n\]

donde\(A\) está la amplitud de tensión,\(n\) es el exponente de endurecimiento y\(\epsilon_o\) es el parámetro de desplazamiento de deformación.

En muchos problemas prácticos la magnitud de la deformación plástica es lodo mayor que el parámetro\(\epsilon_o\), dando lugar a una ley de endurecimiento por potencia más simple, ampliamente utilizada en la literatura.

\[\sigma = A \epsilon^n \]

Para la mayoría de los metales el exponente\(n\) es el rango de\(n = 0.1 - 0.3\), y la amplitud puede variar mucho, dependiendo del grado del acero. Una descripción de la carga inversa y la carga de plástico en bicicleta está fuera del alcance de las presentes notas de conferencia.

11.1.2.png — Figura\(\PageIndex{2}\): La curva tensión-deformación medida experimentalmente y el ajuste por la ley del veloz.

Varias otras aproximaciones de la curva de tensión-deformación real del material son de uso común y algunas de ellas se muestran en la Figura (\(\PageIndex{3}\)).

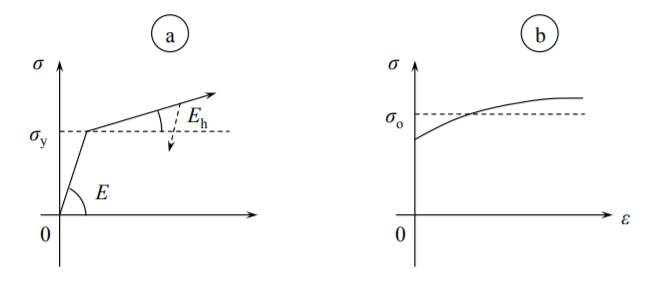
11.1.3.png — Figura\(\PageIndex{3}\): Material de endurecimiento elástico-lineal (a) y material de endurecimiento rígido-plástico (b).

Se obtiene una simplificación adicional considerando el valor promedio\(\sigma_o\) de la curva tensión-deformación, ilustrada en la Figura (\(\PageIndex{3b}\)). Este concepto dio origen al concepto del tiempo característico del material rígido-perfectamente plástico, representado en la Figura (11.2.1).

El modelo material mostrado en la Figura (11.2.1) se adopta en el desarrollo del análisis límite de estructuras. La extensión del concepto de la curva de endurecimiento al caso 3-D se presentará posteriormente, luego de derivar la expresión para la condición de rendimiento.