11.10: Ejemplo del diseño frente al primer rendimiento
- Page ID
- 85196
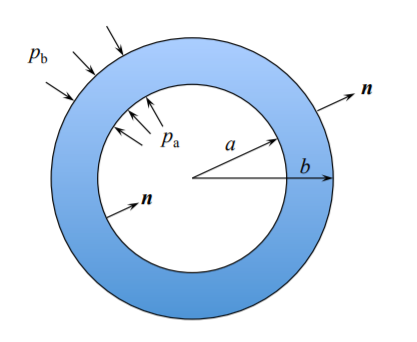
La seguridad de los recipientes a presión y los sistemas de tuberías es fundamental en el diseño de instalaciones marinas, químicas y nucleares. El problema más simple en esta clase de estructuras es una tubería gruesa cargada por una presión interna\(p\). Se supone que el tubo es infinitamente largo y los radios interno y externo se denotan respectivamente por\(a\) y\(b\). En el sistema de coordenadas cilíndricas\((r, \theta, z), \sigma_{zz} = 0\) para el tubo corto de extremo abierto\(\sigma_{rr} = \sigma_r\) y y\(\sigma_{\theta\theta} = \sigma_{\theta}\) son las principales tensiones radiales y circunferenciales. El material es elástico hasta el punto del primer rendimiento. El objetivo es determinar la ubicación donde se produce el primer rendimiento y la presión crítica correspondiente\(p_y\).
La ecuación gobernante se deriva anotando tres grupos de ecuaciones:
Relación geométrica:
\[\epsilon_r = \frac{d}{dr} u, \quad \epsilon_{\theta} = \frac{u}{r} \]
donde\(u\) es la componente radial del vector de desplazamiento,\(u = u_r\). El componente de aro es cero debido a la simetría axial.
Equilibrio:
\[\frac{d}{dr} \sigma_r + \frac{\sigma_r − \sigma_{\theta}}{r} = 0 \]
Ley de elasticidad:
\[\sigma_r = \frac{E}{1 − \nu^2} (\epsilon_r + \nu\epsilon_{\theta}) \]
\[\sigma_{\theta} = \frac{E}{1 − \nu^2} (\epsilon_{\theta} + \nu\epsilon_r) \]
Hay cinco ecuaciones para cinco incógnitas,\(\sigma_r\),\(\sigma_{\theta}\),\(\epsilon_r\),\(\epsilon_{\theta}\) y\(u\). Resolviendo el sistema anterior para\(u\), uno obtiene
\[r^2 \frac{d^2}{dr^2} u + r \frac{d}{dr} u − u = 0 \]
La solución de esta ecuación es
\[u(r) = C_1r + \frac{C_2}{r} \]
donde\(C_1\) y\(C_2\) son constantes de integración que se determinarán a partir de las condiciones de contorno. La condición de límite de tensión y desplazamiento para este problema son
\[(T − \sigma_r) = 0 \quad \text{ or } \quad \delta u = 0 \]
En el caso de carga de presión, se aplica la condición límite de tensión:
\[\text{at } r = a \quad \sigma_r = −p_a \]
\[\text{at } r = b \quad \sigma_r = −p_b \]
El signo menos aparece debido a que la tracción superficial\(T\), que en nuestro caso es carga de presión, actúa en sentido contrario a los vectores normales unitarios n, ver Figura (12.15). En el presente caso de presión interna,\(\sigma_r(r = a) = −p\) y\(\sigma_r(r = b) = 0\). La tensión radial se calcula a partir de las ecuaciones (11.5.3) y (11.6.2-11.6.3)
\[\sigma_r = \frac{E}{1 − \nu^2} \left[(1 + \nu)C_1 − (1 − \nu) \frac{C_2}{r^2} \right] \]
Las constantes de integración se pueden calcular fácilmente a partir de dos condiciones límite, y la solución final para las tensiones es
\[\sigma_r(r) = \frac{a^2p}{b^2 − a^2} \left(1 − \frac{b^2}{r^2} \right) \]
\[\sigma_{\theta}(r) = \frac{a^2p}{b^2 − a^2} \left(1 + \frac{b^2}{r^2} \right) \]
Al eliminar el término\((b/r)^2\) entre las dos ecuaciones anteriores se obtiene el perfil en línea recta de las tensiones, que se muestra en la Figura (\(\PageIndex{2}\)).
\[\sigma_r + \sigma_{\theta} = 2p \frac{1}{\left(\frac{b}{a}\right)^2 − 1} \]
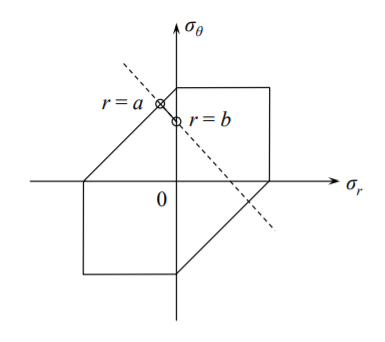
Se ve que el perfil de tensión está completamente en el segundo cuadrante y el tubo alcanza el rendimiento en\(r = a\), para lo cual las tensiones son
\[\sigma_r = −p \]
\[\sigma_{\theta} = p \frac{b^2 + a^2}{b^2 − a^2} \]
En el caso de la condición de rendimiento de Tresca
\[|\sigma_{\theta} − \sigma_r| = \sigma_y \]
La presión de fluencia adimensional es
\[\frac{p}{\sigma_y} = \frac{1}{2} \left[ 1 − \left(\frac{a}{b}\right)^2 \right] \]
La condición de rendimiento de von Mises predice
\[\frac{p}{\sigma_y} = \frac{1 − (a/b)^2}{\sqrt{3 + (a/b)^4}} \]
Por ejemplo, si\(\frac{a}{b} = \frac{1}{2}\), la primera presión de fluencia de acuerdo con la condición de rendimiento de von Mises es\(\frac{p_y}{\sigma_y} = \frac{3}{7}\) mientras que el criterio de rendimiento de Tresca predice\(\frac{p_y}{\sigma_y} = \frac{3}{8}\). La diferencia entre los dos casos anteriores es del 14%.


