1.31: Problemas

1. Supongamos que disparamos electrones a través de una sola hendidura con ancho d. En la pantalla de visualización detrás de la abertura, los electrones formarán un patrón. Derive y dibuja la expresión para la intensidad en la pantalla de visualización. Expresar todos los supuestos necesarios.

Figura\(\PageIndex{1}\): La geometría de un experimento de difracción de hendidura única.

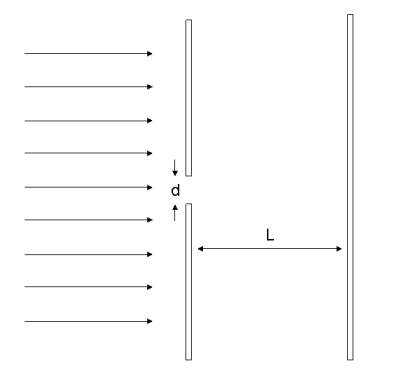
¿En qué se diferencia este patrón del patrón con dos hendiduras discutidas en clase?

2. Compara los diferentes patrones en la pantalla de visualización con d = 20Å y L = 100nm para electrones disparados con longitudes de onda de 10Å, 100Å y 1000Å. Explique.

3. Mostrar que un desplazamiento en la posición de un bloque de ondas por\(x_{0}\) es equivalente a multiplicar la representación del espacio k por\(\text{exp}[-ikx_{0}]\). También, mostrar que un desplazamiento en la representación del espacio k por\(k_{0}\) es equivalente a multiplicar la posición del conjunto de ondas por\(\text{exp}[-ik_{0}x]\). Mostrar que relaciones similares se mantienen para los turnos en tiempo y frecuencia.

4. Encuentra\(|F(\omega)|^{2}\) dónde\(F(\omega)\) está la Transformada de Fourier de una decadencia exponencial:

\[ F(\omega)= \mathcal{F}[e^{-at}u(t)] \nonumber \]

donde u (t) es la función de paso de unidad.

5. Demuestre que si

\[ (\Delta x)^{2} = \langle x^{2}\rangle - \langle x\rangle^{2} \nonumber \]

entonces

\[ \Delta x=\sigma \nonumber \]

donde

\[ \psi(x)=\text{exp}[-\frac{1}{4}\frac{(x-x_{0})^{2}}{\sigma^{2}}] \nonumber \]

6. Mostrar lo siguiente:

(a)\( \langle k\rangle=\frac{\langle A|k| A\rangle}{\langle A \mid A\rangle}=\frac{\left\langle\psi\left|-i \frac{d}{d x}\right| \psi\right\rangle}{\langle\psi \mid \psi\rangle} \)

b)\( \langle \omega\rangle=\frac{\langle A|\omega| A\rangle}{\langle A \mid A\rangle}=\frac{\left\langle\psi\left|i \frac{d}{d t}\right| \psi\right\rangle}{\langle\psi \mid \psi\rangle} \)

7. Una partícula libre está confinada para moverse a lo largo del eje x. En el tiempo t=0 la función de onda viene dada por

\ [\ psi (x, t=0) =\ izquierda\ {\ begin {array} {cc}
\ frac {1} {\ sqrt {L}} e^ {i k_ {0} x} &\ frac {-L} {2}\ leq x\ leq\ frac {L} {2}\\
0 &\ text {de lo contrario}
\ end {array}\ derecha. \ nonumber\]

a) ¿Cuál es el valor más probable del impulso?

b) ¿Cuáles son los valores menos probables de impulso?

(c) Hacer un boceto aproximado de la función de onda en k-espacio, A (k, t =0).

8. El conmutador de dos operadores\(\hat{A}\) y\(\hat{B}\) se define como

\[ [\hat{A},\hat{B}]=\hat{A}\hat{B}-\hat{B}\hat{A} \nonumber \]

Evaluar los siguientes conmutadores:

(a)\([\hat{x},\hat{x}^{2}]\)

b)\([\hat{p},\hat{p}^{2}]\)

c)\([\hat{x}^{2},\hat{p}^{2}]\)

d)\([\hat{x}\hat{p},\hat{p}\hat{x}]\)

9. Considera la función de onda

\[ \psi(x)=\exp \left[-\frac{1}{2} \frac{x^{2}}{\sigma^{2}}(1+i C)\right] \nonumber \]

Demostrar que

\[ \left|\sigma_{x}\right|\left|\sigma_{k}\right| \geq \frac{1}{2} \sqrt{1+C^{2}} \nonumber \]

(Pista: Demuéstralo\( |\sigma_{k}^{2}|=\frac{\langle \psi|-\frac{d^{2}}{dx^{2}}|\psi \rangle}{\langle \psi|\psi \rangle} \)

10. Para el pozo cuadrado finito que se muestra a continuación, calcule los coeficientes de reflexión y transmisión (E > 0).

Figura\(\PageIndex{2}\): Un pozo de potencial finito.

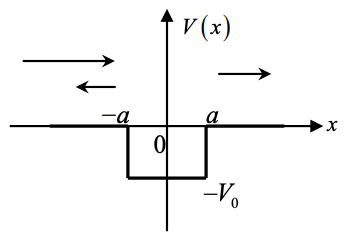
11. Considerar un electrón en el estado fundamental de un pozo cuadrado infinito de ancho L. ¿Cuál es el valor de expectativa de su velocidad? ¿Cuál es el valor de expectativa de su energía cinética? ¿Existe un conflicto entre tus resultados?

12. Derivar los coeficientes de reflexión y transmisión para el potencial\(V(x)=A\delta(x)\), donde A>0.

Figura\(\PageIndex{3}\): Un potencial de función delta.

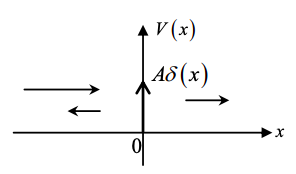
Un método a resolver es tomar la ecuación de Schrödinger con\(V(x)=A\delta(x)\)

\[ -\frac{\hbar^{2}}{2 m} \frac{\partial^{2} \psi(x)}{\partial x^{2}}+A \delta(x) \psi(x)=E \psi(x) \nonumber \]

e integrando ambos lados de\(-\epsilon\) a\(\epsilon\) para\(\epsilon\) muy pequeños para obtener la restricción

\[ -\frac{\hbar^{2}}{2 m} \int_{-\varepsilon}^{+\varepsilon} \frac{\partial^{2} \psi(x)}{\partial x^{2}} d x+A \psi(0) \simeq 2 \varepsilon E \psi(0) \simeq 0 \nonumber \]

\( \left.\Rightarrow \frac{d \psi}{d x}\right|_{x=\varepsilon}-\left.\frac{d \psi}{d x}\right|_{x=-\varepsilon}=\frac{2 m A}{\hbar^{2}} \psi(0) \)

13. Considera dos pozos cuánticos cada uno con ancho w separados por distancia d.

Figura\(\PageIndex{4}\): La estructura de los pozos cuánticos.

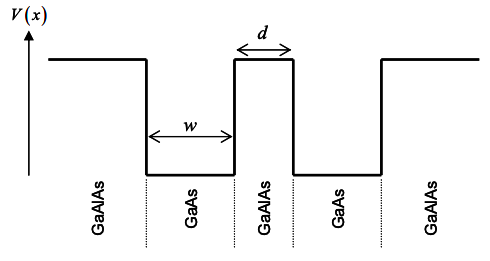
(a) A partir de su comprensión de las funciones de onda para una partícula en una caja, graficar la densidad de probabilidad aproximada para cada uno de los dos modos de energía más bajos para este sistema cuando los dos pozos cuánticos están aislados entre sí.

(b) Trazar los dos modos de menor energía cuando los dos pozos cuánticos se acercan entre sí de tal manera que d\ llw?

(c) A continuación deseamos tomar una rebanada delgada de otro material e insertarlo en la estructura anterior (donde d\ llw) para matar uno de los dos modos de la parte (b) pero dejar al otro inalterado. ¿Cómo elegiría el material (en comparación con los materiales ya presentes en la estructura) y dónde debería colocarse este nuevo material?