5.6: El límite de carga cero
- Page ID
- 84205
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Como vimos en la Parte 3, los cambios inducidos por carga en los niveles de energía de los conductores pueden complicar significativamente el cálculo de las características IV. La ecuación (5.4.5) demuestra que la carga se puede descuidar si la capacitancia cuántica es mucho menor que la capacitancia electrostática, es decir\(C_{Q} \ll C_{ES}\). Por ejemplo, en la Ecuación (5.4.5), si\(C_{Q} \ll C_{ES}\) entonces la carga,\(\delta N \rightarrow 0\).
En el límite de carga cero, la ecuación (5.5.1) se reduce a
\[ U=-qV_{GS} \nonumber \]
es decir, en este límite el potencial del canal simplemente rastrea el sesgo de puerta.
Así, en el límite de carga cero, podemos determinar la corriente directamente a partir de la Ecuación (5.3.6), con el potencial de canal\(U=-qV_{GS}\).
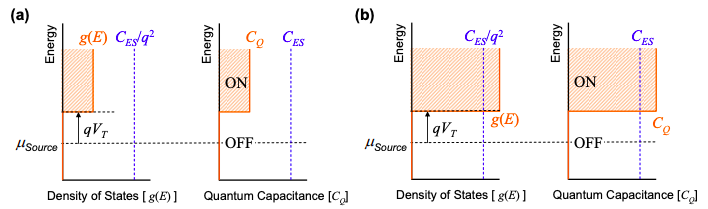
El límite de carga cero casi siempre se mantiene para aisladores y transistores en el estado OFF porque la densidad de estados en el nivel Fermi es pequeña en ambos ejemplos. Determinar si un transistor permanece en el límite de carga cero en el estado ON requiere una comparación de\(C_{Q}\) y\(C_{ES}\). Los dispositivos a granel rara vez operan dentro del límite de carga cero en el estado ON. Pero muchos conductores pequeños contienen relativamente pocos estados en el nivel Fermi incluso en el estado ON, tal que\(C_{Q} \ll C_{ES}\) incluso cuando fluye una corriente de canal significativa.