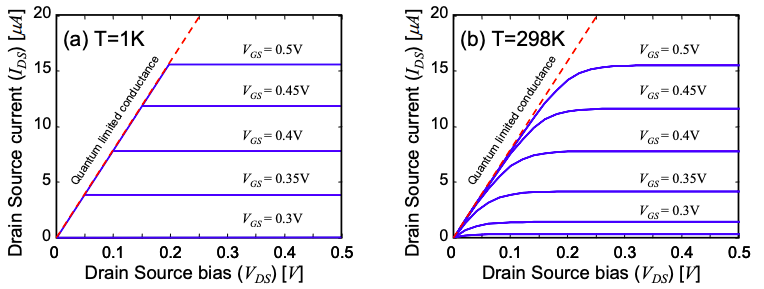
5.12: Características de corriente-voltaje FET de alambre cuántico balístico en T = 0K.

Las capacitancias electrostáticas se muestran en la Figura 5.11.2 utilizando el modelo de puntos cuánticos del cable cuántico. En este ejemplo ignoramos las capacitancias de fuente y drenaje. El condensador de puerta se definió en la Figura 5.10.1 como\(C_{G} = \text{1 aF per nanometer of gate length}\).

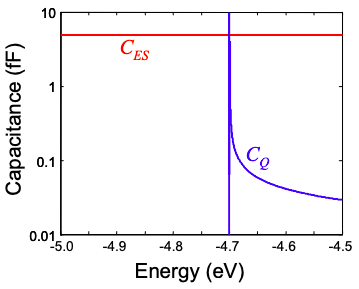
Comparamos las capacitancias cuánticas y electrostáticas en la Figura 5.12.1, encontramos que el cable monomodo tiene relativamente pocos estados, de ahí que su capacitancia cuántica es pequeña, y por encima del borde de banda opera en el régimen de carga/aislante cero; incluso en el estado ON los efectos de carga son insignificantes y podemos tomar \(U = -qV_{GS}\).

Figura\(\PageIndex{1}\): Una comparación entre las capacitancias electrostáticas y cuánticas muestra que eso\(C_{Q} \gg C_{ES}\) solo en el borde de la banda de conducción. Pero a medida que el canal se llena de carga, el cable vuelve al régimen aislante.

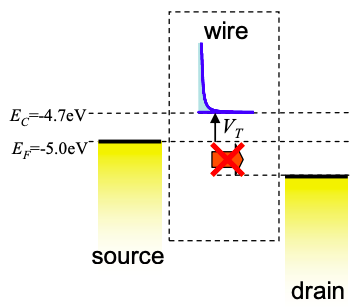
En el sesgo directo (cuando el potencial de drenaje es menor que la fuente), existen tres regímenes de operación:

APAGADO:\(V_{GS} < V_{T}\)

Definamos el voltaje umbral como la diferencia de potencial entre la fuente y el mínimo de banda de conducción. Así, en este ejemplo,\(V_{T} = 0.3 V\). Recordemos que el potencial de puerta es relativo al potencial de origen. Entonces\(V_{GS} < V_{T}\), cuando, los electrones no pueden ser inyectados desde la fuente. Por lo tanto, no puede fluir corriente para voltajes de drenaje positivos. Este es el estado OFF del FET.

Tenga en cuenta que la corriente de drenaje de la fuente puede fluir\(T > 0K\) ya que la cola de la distribución de Fermi para los electrones en la fuente se solapa con los estados en el cable. La corriente sigue la Ecuación (5.8.6).

Figura\(\PageIndex{2}\): Línea de energía para FET en el estado OFF. No hay estados de canal entre los potenciales químicos de origen y drenaje.

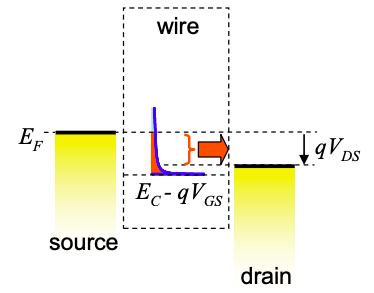
El régimen lineal:\(V_{GS} > V_{T},\ V_{DS} < V_{GS}-V_{T}\)

Esto se conoce como el régimen lineal porque la corriente se escala linealmente con el potencial de la fuente de drenaje. La ecuación (5.10.6) reduce a

\[ I_{DS} = \frac{2q^{2}}{h} V_{DS} \nonumber \]

Obsérvese que el FET exhibe el límite cuántico de conducción en este régimen. Su transconductancia, sin embargo, es cero.

Figura\(\PageIndex{3}\): En el régimen lineal, la corriente está limitada por el potencial de drenaje de la fuente.

Saturación:\(V_{GS} > V_{T},\ V_{DS} > V_{GS}-V_{T}\)

Una vez que el potencial de drenaje excede\(V_{GS}-V_{T}\), toda la carga en el canal se descompensa y se inyecta en el drenaje. Por lo tanto, la corriente está limitada por el potencial de puerta. Esto se conoce como saturación.

\[ I_{DS} = \frac{2q^{2}}{h} (V_{GS}-V_{T}) \nonumber \]

La transconductancia para un cable monomodo en saturación es

\[ g_{m} = \frac{2q^{2}}{h} \nonumber \]

Figura\(\PageIndex{4}\): En el régimen de saturación, la corriente está limitada por el potencial de fuente de puerta.

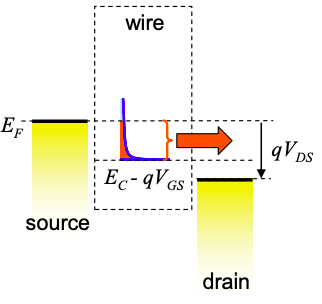
La Figura 5.21.5 representa las características de sesgo directo del FET tanto a T = 0K como a temperatura ambiente. A temperatura ambiente, las características se determinaron numéricamente ya que la transición de regímenes lineales a regímenes de saturación se ve borrosa por la activación térmica de electrones por encima del nivel Fermi.

Figura\(\PageIndex{5}\): Características de polarización directa para un FET de cable cuántico a (a) T = 0K y (b) temperatura ambiente.