6.3: Análisis de malla

El análisis de malla es similar al análisis nodal en que puede manejar circuitos complejos de múltiples fuentes. De alguna manera es la imagen especular del análisis ganglionar. Mientras que el análisis nodal utiliza la ley actual de Kirchhoff para crear una serie de sumas de corriente en varios nodos, el análisis de malla utiliza la ley de voltaje de Kirchhoff para crear una serie de ecuaciones de bucle que se pueden resolver para corrientes de malla. La corriente a través de cualquier componente particular puede ser una corriente de malla o una combinación de corrientes de malla. Por supuesto, una vez que se encuentran esas corrientes, es un salto corto para encontrar cualquier voltaje deseado. La malla tiene una limitación que nodal no tiene: El análisis de malla requiere que el circuito sea plano. Es decir, el circuito debe poder dibujarse sobre una superficie plana sin que ningún cable se cruce entre sí. Otra forma de verlo es que se pueden dibujar circuitos planos para que aparezcan como una serie de cajas que chocan entre sí. Para hacerse una idea visceral de esta noción, agarra un trozo de papel y coloca cuatro puntos sobre él. Intenta dibujar una línea de cada punto a cada otro punto pero sin cruzar ninguna línea. Después de algunos intentos, deberías tener éxito. Ahora pruébalo con cinco puntos. No puedes hacerlo a menos que “dibujes en el aire” y saltes por encima de otras líneas. Obviamente, eso es posible con circuitos reales porque son 3D. Por lo tanto, hay circuitos que no se pueden resolver usando malla.

Considera el circuito de la Figura\(\PageIndex{1}\). Este circuito tiene dos fuentes de voltaje y no se puede simplificar aún más, aunque puede resolverse mediante superposición o análisis nodal. Para el análisis de malla, comenzamos designando un conjunto de bucles actuales. Estos bucles deben ser mínimos en tamaño y juntos cubrir todos los componentes al menos una vez. Por convención, los bucles se dibujan con una dirección de referencia en sentido horario. No hay nada mágico en que estén en el sentido de las agujas del reloj, es solo cuestión de consistencia. La versión anotada del circuito se vuelve a dibujar en la Figura\(\PageIndex{2}\).

Figura\(\PageIndex{1}\): Un circuito simple de dos fuentes.

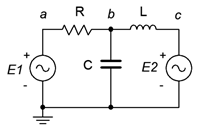
Aquí tenemos dos corrientes de bucle,\(i_1\) y\(i_2\). Tenga en cuenta que todos los componentes existen en al menos un bucle (y a veces en más de un bucle, como condensador\(C\)). Dependiendo de los valores del circuito, una o más de estas direcciones de bucle pueden ser de hecho opuestas a la realidad. Esto no es un problema. Si la dirección de referencia verdadera es opuesta, entonces las corrientes aparecerán como valores negativos, y así sabemos que la dirección de referencia real es en sentido antihorario. Solo recuerda que un resultado positivo significa un sentido horario y negativo indica en sentido antihorario.

Figura\(\PageIndex{2}\): Circuito con bucles de malla y polaridades de voltaje dibujadas.

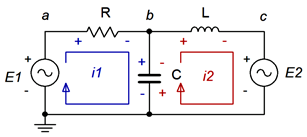
Comenzamos por escribir ecuaciones KVL para cada bucle.

Bucle 1:\(E_1\) = voltaje a través de\(R\) + voltaje a través de\(X_C\)

Bucle 2:\(−E_2\) = voltaje a través de\(X_C\) + voltaje a través de\(X_L\)

Tenga en cuenta que\(E_2\) es negativo ya que\(i_2\) se dibuja fluyendo fuera de su terminal negativo. Ahora expanda los términos de voltaje usando la ley de Ohm. La resistencia y el inductor ven cada uno una sola corriente,\(i_1\) y\(i_2\), respectivamente. El condensador experimenta ambas corrientes. Desde la perspectiva del bucle 1,\(i_2\) está fluyendo en sentido contrario. Así, la corriente neta es\(i_1 − i_2\). Desde la perspectiva del bucle 2,\(i_1\) está fluyendo en la dirección opuesta y así la corriente neta es\(i_2 − i_1\). Las polaridades de tensión de referencia refuerzan esta noción.

Bucle 1:\(E_1 = i_1 R + (i_1 − i_2)(−jX_C)\)

Bucle 2:\(−E_2 = i_2 (jX_L) + (i_2 − i_1)(−jX_C)\)

Multiplicando y cobrando términos rendimientos:

Bucle 1:\(E_1 = (R −jX_C) i_1 − (−jX_C) i_2\)

Bucle 2:\(−E_2 = − (−jX_C) i_1 + (jX_L −jX_C) i_2\)

Como se conocen los valores de los componentes y los voltajes fuente, tenemos dos ecuaciones con dos incógnitas. Estos se pueden resolver para\(i_1\) y\(i_2\) utilizando las técnicas de solución de ecuaciones simultáneas de su elección.

Ejemplo\(\PageIndex{1}\)

Para el circuito de la Figura\(\PageIndex{3}\), determinar vb y vc. Las fuentes son:\(E_1 = 9\angle 0^{\circ}\) voltios y\(E_2 = 12\angle −90^{\circ}\) voltios.

Figura\(\PageIndex{3}\): Circuito por Ejemplo\(\PageIndex{1}\).

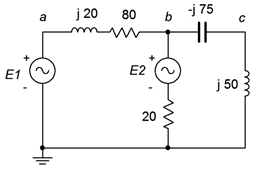
Comenzamos etiquetando nuestros bucles, como se muestra en la Figura\(\PageIndex{4}\). Cada bucle generará una ecuación basada en una suma KVL alrededor de ese bucle. Numeraremos los componentes de izquierda a derecha, como de costumbre.

Figura\(\PageIndex{4}\): Circuito de la Figura\(\PageIndex{3}\) con bucles de corriente dibujados.

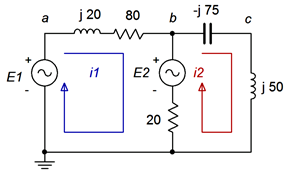
Para el bucle 1:

\[E_1 −E_2 = ( jX_{L1}+R_1 )i_1+R_2 (i_1 −i_2 ) \nonumber \]

\[E_1 −E_2 = (R_1+R_2+jX_{L1})i_1 −R_2 i_2 \nonumber \]

\[9\angle 0^{\circ} V −12\angle −90^{\circ} V = (20+80+j 20 \Omega )i_1 −20\Omega i_2 \nonumber \]

\[15\angle 53.1^{\circ} V = (100+j 20 \Omega )i_1 −20\Omega i_2 \nonumber \]

Repita para el bucle 2:

\[E_2 = (− jX_C+jX_{L2})i_2+R_2 (i_2 −i_1 ) \nonumber \]

\[E_2 =−R_2 i_1+(R_2 − jX_C+jX_{L2})i_2 \nonumber \]

\[12\angle −90^{\circ} V = −20\Omega i_1 +(20 − j 75+j 50\Omega )i_2 \nonumber \]

\[12\angle −90^{\circ} V = −20\Omega i_1 +(20 − j 25\Omega )i_2 \nonumber \]

Las dos ecuaciones de bucle son:

\[15\angle 53.1^{\circ} V = (100+j 20\Omega )i_1 −20\Omega i_2 \nonumber \]

\[12\angle −90^{\circ} V = −20\Omega i_1 +(20− j 25\Omega )i_2 \nonumber \]

Las ecuaciones muestran simetría diagonal. Las corrientes son\(i_1 = 0.1785\angle 19.9^{\circ}\) amperios y\(i_2 = 0.3529\angle −21.4^{\circ}\) amperios. Para encontrar los voltajes\(v_b\) y\(v_c\), solo necesitamos aplicar la ley de Ohm. El voltaje\(v_c\) es el potencial a través del\(j50 \Omega\) inductor.

\[v_c = i_2\times jX_{L2} \nonumber \]

\[v_c = 0.3529\angle −21.4^{\circ} A\times j 50\Omega \nonumber \]

\[v_c = 17.64\angle 68.6^{\circ} V \nonumber \]

El potencial\(v_b\) se encuentra de manera similar.

\[v_b = i_2\times (− jX_C+jX_{L2}) \nonumber \]

\[v_b = 0.3529\angle −21.4^{\circ} \times (− j 75\Omega +j 50 \Omega ) \nonumber \]

\[v_b = 8.823\angle −111.4^{\circ} V \nonumber \]

Para la verificación, también podemos encontrar\(v_b\) restando el voltaje desarrollado a través del par inductor/resistor en serie de la primera fuente.

\[v_b = E_1 − i_1\times (R_1+jX_{L1}) \nonumber \]

\[v_b = 9\angle 0^{\circ} V − 0.1785\angle 19.9^{\circ} A\times (80 +j 20 \Omega ) \nonumber \]

\[v_b=8.823\angle −111.4^{\circ} V \nonumber \]

Ejemplo\(\PageIndex{2}\)

En el circuito de Figura\(\PageIndex{5}\), encuentra\(v_b\). \(E = 10\angle 0^{\circ}\)pico de voltios a una frecuencia de 10 kHz.

El circuito es una red de puentes. A pesar de que solo tiene una sola fuente de voltaje, las técnicas básicas serie-paralelo no funcionarán aquí. El análisis nodal también puede funcionar aquí como puede la conversión delta-Y, sin embargo, la malla es una excelente opción para este diseño.

Figura\(\PageIndex{5}\): Circuito por Ejemplo\(\PageIndex{2}\).

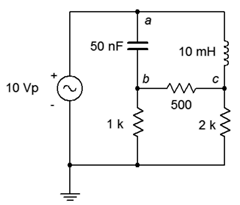
Comenzamos por encontrar los valores de reactancia. Usando las fórmulas de reactancia estándar encontramos que\(X_L = j628.3 \Omega\) y\(X_C = −j318.3 \Omega\). Después de sustituirlos en el circuito original y definir los bucles, tenemos Figura\(\PageIndex{6}\).

Figura\(\PageIndex{6}\): Circuito de la Figura\(\PageIndex{5}\) con valores de reactancia y bucles de corriente dibujados.

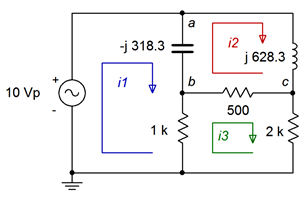
Tenemos tres bucles con tres corrientes desconocidas, y por lo tanto tres ecuaciones. Numeraremos las resistencias de izquierda a derecha. Para el bucle 1:

\[E = v_C+v_{R1} \nonumber \]

\[E =− jX_C (i_1 −i_2 )+R_1 (i_1 −i_3 ) \nonumber \]

\[E = (R_1 − jX_C )i_1 −(− jX_C )i_2 −R_1 i_3 \nonumber \]

\[10\angle 0^{\circ} V = (1k \Omega − j 318.3\Omega )i_1+j318.3 \Omega i_2 −1k \Omega i_3 \nonumber \]

Para el bucle 2:

\[0 = v_C+v_L+v_{R2} \nonumber \]

\[0 =− jX_C (i_2 −i_1 )+jX_L (i_2 −i_3 )+jX_L i_3 \nonumber \]

\[0 =−(− jX_C )i_1+(R_2+X_L − jX_C )i_2 −R_2 i_3 \nonumber \]

\[0 =−(− j 318.3\Omega )i_1+(500+j 628.3 − j 318.3\Omega )i_2 −500\Omega i_3 \nonumber \]

\[0 = j 318.3\Omega i_1+(500+j 310\Omega )i_2 −500\Omega i_3 \nonumber \]

Para el bucle 3:

\[0 = v_{R1} + v_{R2} + v_{R3} \nonumber \]

\[0 = R_1 (i_3 −i_1 )+R_2 (i_3 −i_2 )+R_3 i_3 \nonumber \]

\[0 =−R_1 i_1 −R_2 i_2+(R_1+R_2+R_3 )i_3 \nonumber \]

\[0 =−1 k\Omega i_1 −500 \Omega i_2+(1k \Omega +500\Omega +2k \Omega )i_3 \nonumber \]

\[0 =−1 k\Omega i_1 −500 \Omega i_2+3.5k \Omega i_3 \nonumber \]

El conjunto final de ecuaciones es:

\[10\angle 0^{\circ} V = (1k \Omega − j 318.3\Omega )i_1+j 318.3 \Omega i_2 −1k \Omega i_3 \nonumber \]

\[0 = j 318.3\Omega i_1+(500+j 310 \Omega )i_2 −500\Omega i_3 \nonumber \]

\[0 =−1 k\Omega i_1 −500 \Omega i_2+3.5k \Omega i_3 \nonumber \]

El sistema de ecuaciones tiene simetría diagonal. Los resultados son:\(i_1 = 10.24E-3\angle 16^{\circ}\) amperios,\(i_2 = 6.754E-3\angle −85.7^{\circ}\) amperios y\(i_3 = 2.888E-3\angle −3.13^{\circ}\) amperios.

Porque\(v_b\), esto es solo el voltaje a través de la\(\Omega \) resistencia de 1 k. Tenga en cuenta que un par de corrientes de malla (\(i_1\)y\(i_3\)) están fluyendo a través de esa resistencia, por lo que debemos determinar el valor neto de la corriente. Si asumimos que la polaridad de referencia para\(v_b\) es positiva, eso coincide con la dirección de\(i_1\), y así la corriente neta debe ser\(i_1 − i_3\). El resultado son\(i_{net} = 7.57E−3\angle 23.2^{\circ}\) amperios. Por lo tanto,\(v_b = 7.57\angle 23.2^{\circ}\) voltios.

Simulación por Computadora

La figura\(\PageIndex{7}\) muestra el circuito puente de Ejemplo\(\PageIndex{2}\) capturado en un simulador. Esto se utilizará para verificar el resultado calculado.

Figura\(\PageIndex{7}\): Circuito de Figura\(\PageIndex{5}\) en un simulador.

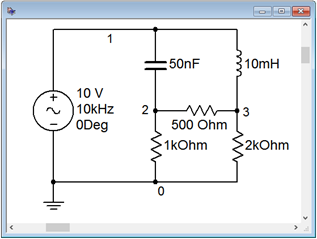
Se ejecuta un análisis transitorio en el circuito, trazando el nodo 2 que corresponde a\(v_b\), y el nodo 1, el voltaje de entrada, que es útil para la referencia de fase.

Figura\(\PageIndex{8}\): Análisis transitorio para el circuito de la Figura\(\PageIndex{7}\).

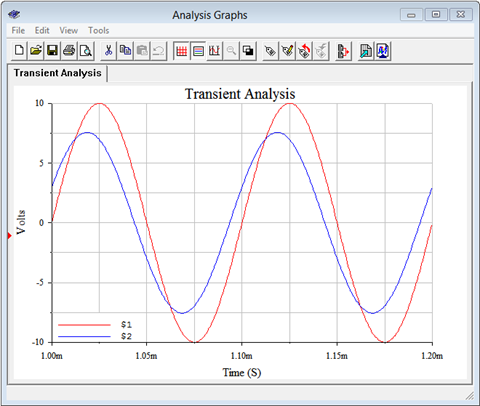
Examinando la gráfica, podemos ver que el voltaje del nodo 2 está justo por encima del pico de 7.5 voltios, según se calcula. Además, esta forma de onda lleva la forma de onda de entrada por poco más de un cuarto de división. Como esta trama muestra cuatro divisiones por ciclo, cada división es de 90 grados. Esto indica un desplazamiento de fase inicial o positivo en el rango bajo de 20 grados, y eso corrobora muy bien el valor calculado de 23.2 grados.

Método de Inspección

Al igual que el análisis nodal, es posible que el sistema de ecuaciones se pueda obtener directamente a través de la inspección. Esto es cierto solo si el circuito no contiene fuentes de corriente. Observe el conjunto final de ecuaciones derivadas en Ejemplo\(\PageIndex{2}\) de la Figura\(\PageIndex{6}\). Surgirá un patrón claro. Para generar una ecuación para un bucle dado, simplemente concéntrese en ese bucle y haga las siguientes preguntas: ¿Cuál es el voltaje total de la fuente en este bucle? Esto produce la constante de voltaje en el lado izquierdo del signo igual. A continuación, suma los valores de resistencia y reactancia en el bucle bajo inspección. Esto arroja el coeficiente para ese término actual. Para los otros coeficientes de corriente, sumar las resistencias y reactancias que son comunes entre el bucle bajo inspección y los otros bucles (por ejemplo, para el bucle 1,\(X_C\) es común con el bucle 2). Estos valores siempre serán negativos (surge una excepción con un “doble negativo”, como se ve con el condensador). Como es habitual, el conjunto de ecuaciones producidas debe exhibir simetría diagonal.

Si bien es posible extender esta técnica para incluir fuentes de corriente, generalmente es más fácil y menos propenso a errores convertir las fuentes de corriente en fuentes de voltaje. Entonces el proceso puede continuar con el método de inspección directa descrito anteriormente. Por último, es importante recordar que el número de bucles determina el número de ecuaciones a resolver. Este método se ilustrará en el siguiente ejemplo.

Ejemplo\(\PageIndex{3}\)

Para el circuito de la Figura\(\PageIndex{9}\), encontrar\(v_b\) y la corriente a través de la\(\Omega \) resistencia 15. \(E_1 = 10\angle 0^{\circ}\)pico de voltios y pico de\(E_2 = 20\angle 90^{\circ}\) voltios.

Figura\(\PageIndex{9}\): Circuito por Ejemplo\(\PageIndex{3}\).

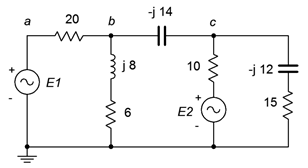
Identificamos y etiquetamos tres bucles, como se muestra en la Figura\(\PageIndex{10}\). Este circuito utiliza solo fuentes de voltaje y ninguna fuente de corriente. Por lo tanto, podemos aplicar el método de inspección sin esfuerzo adicional.

Figura\(\PageIndex{10}\): Circuito de la Figura\(\PageIndex{9}\) con bucles de corriente dibujados.

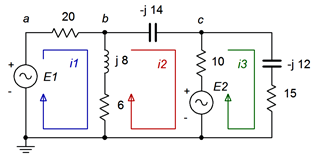
Comenzamos en el bucle 1 y sumamos todas las fuentes de voltaje. La única fuente es\(E_1\).

\[10\angle 0^{\circ} V = \dots \nonumber \]

Ahora sumamos todas las resistencias y reactancias en este bucle. Este es el coeficiente para el primer término actual.

\[10\angle 0^{\circ} V =(20\Omega +6\Omega +j 8\Omega )i_1 \dots \nonumber \]

Continuamos el proceso determinando los componentes que están en común entre este bucle y el siguiente bucle. Recuerda, este coeficiente es negativo.

\[10\angle 0^{\circ} V =(20\Omega +6\Omega +j 8\Omega )i_1 −(6\Omega +j 8\Omega )i_2 \dots \nonumber \]

Repetimos el proceso determinando los componentes comunes con el siguiente bucle. Este coeficiente es negativo. En esta situación, no hay componentes en común entre los bucles 1 y 3. Dejaremos en marcador de posición con un coeficiente de cero, solo como recordatorio de que no olvidamos nada y también para asegurar que los coeficientes en el conjunto final de ecuaciones se alineen muy bien.

\[10\angle 0^{\circ} V = (26+j 8\Omega )i_1 −(6+j 8\Omega )i_2 −0i_3 \nonumber \]

Ahora pasamos al bucle 2 y repetimos la secuencia de pasos. Solo hay una fuente\(E_2\), y se muestra negativa a medida que la corriente\(i_2\) de malla fluye fuera de su terminal negativo. El resultado es:

\[−20\angle 90^{\circ} V =−(6+j 8\Omega )i_1+(6+10+j8 − j 14 \Omega )i_2 −10\Omega i_3 \nonumber \]

\[−20\angle 90^{\circ} V =−(6+j 8\Omega )i_1+(16 − j 6\Omega )i_2 −10\Omega i_3 \nonumber \]

Y finalmente el tercer bucle. Aquí la segunda fuente aparece como positiva.

\[20 \angle 90^{\circ} V =−0i_1−10\Omega i_2 −(10+15− j 12\Omega )i_3 \nonumber \]

\[20 \angle 90^{\circ} V =−0i_1−10\Omega i_2 −(25− j 12\Omega )i_3 \nonumber \]

El sistema de ecuaciones completado es:

\[10\angle 0^{\circ} V = (26+j 8\Omega )i_1 −(6+j8\Omega )i_2 −0i_3 \nonumber \]

\[−20\angle 90^{\circ} V =−(6+j 8\Omega )i_1+(16 − j 6\Omega )i_2 −10\Omega i_3 \nonumber \]

\[20 \angle 90^{\circ} V =−0i_1−10\Omega i_2 −(25 − j 12\Omega )i_3 \nonumber \]

El sistema tiene simetría diagonal. Las corrientes resultantes son:\(i_1 = 0.6131\angle −15.5^{\circ}\) amperios,\(i_2 = 0.6687\angle −49.2^{\circ}\) amperios y\(i_3 = 0.5611\angle 99.3^{\circ}\) amperios.

La corriente a través de la\(\Omega \) resistencia 15 es\(i_3\), así que se hace mucho. En cuanto a\(v_b\), se puede encontrar usando la ley de Ohm como lo\(v_b\) es la conexión en serie de la\(\Omega \) resistencia 6 y el\(j8 \Omega\) inductor multiplicado por la corriente a través de ellos. Esta corriente es el par de corrientes de malla\(i_1\) y\(i_2\). Suponiendo que la polaridad de referencia para\(v_b\) es positiva, esa es la dirección de\(i_1\), y así la corriente neta debe ser\(i_1 − i_2\). El resultado son\(0.375\angle 65.8^{\circ}\) amperios. Por lo tanto,\(v_b = 3.75\angle 119^{\circ}\) voltios. Para verificar esto, podemos restar el voltaje a través de la\(\Omega \) resistencia 20 de\(E_1\). Eso son\(10\angle 0^{\circ}\) voltios menos 20\(\Omega \) veces\(0.6131\angle −15.5^{\circ}\) amperios, o\(3.75\angle 119^{\circ}\) voltios, como se esperaba.

Supermesh

En ocasiones se puede encontrar una fuente de corriente que no tiene impedancia interna asociada, como la del circuito de la Figura\(\PageIndex{11}\). Esto es similar a la situación discutida previamente con el análisis nodal donde una fuente de voltaje no tiene una impedancia interna especificada. Al igual que con nodal, hay dos formas de resolver esta situación. La primera técnica es agregar una impedancia muy grande en paralelo con la fuente de corriente y luego realizar una conversión de fuente en el par para que se pueda utilizar el método de inspección de malla. Cuanto mayor sea el valor de esta impedancia, mayor será la precisión. Como regla general debe ser al menos un par de órdenes de magnitud mayor que cualquier impedancia circundante, y preferiblemente mayor. La segunda técnica es usar supermesh. Una supermalla es un bucle de malla más grande que contiene otros bucles de malla dentro de él.

Consulte el circuito que se muestra en la Figura\(\PageIndex{11}\). En el centro tenemos una fuente de corriente\(I_s\), que carece de una impedancia interna asociada. Dos bucles de malla tradicionales,\(i_1\) y\(i_2\), están etiquetados como de costumbre. El problema aquí es que no podemos usar una caída de\(i_Z\) voltaje basada en la ley de Ohm para\(v_b\). No tenemos forma de expresar esto ya que el voltaje a través\(I_s\) es desconocido. Por otro lado, lo que sí sabemos es que Is debe igualar la combinación de las corrientes de malla originales\(i_1\) y\(i_2\). Es decir, desde la perspectiva del primer bucle,\(I_s = i_2 − i_1\). Recuerde, una o ambas corrientes de malla podrían ser negativas, y así girar en sentido antihorario.

Figura\(\PageIndex{11}\): Circuito para supermalla.

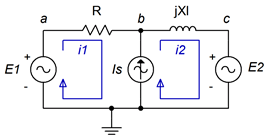
En este punto invocamos la idea de un bucle supermesh. Primero, reemplazamos la fuente de corriente problemática con su impedancia interna ideal, una abierta. Segundo, se dibuja un bucle supermesh que abarca los dos bucles originales. Esto se muestra en la Figura\(\PageIndex{12}\). El bucle de supermalla se muestra en rojo y se etiqueta.

Figura\(\PageIndex{12}\): Supermalla etiquetada.

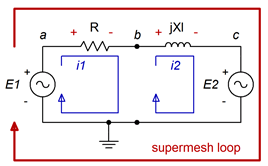
Ahora realizamos una suma KVL alrededor del bucle supermesh, similar a lo que hemos hecho en trabajos anteriores. La diferencia en esta ocasión es que necesitamos reconocer que cada uno de los componentes ve una de las corrientes de malla originales; es decir,\(i_1\) o\(i_2\) aquí. No resolvemos para una corriente supermesh. En cambio, solo usamos el bucle supermesh para definir la suma KVL. La suma sigue:

\[\sum v_{rises} = \sum v_{drops} \nonumber \]

\[E_1 = v_R+v_{XL}+E_2 \nonumber \]

Las caídas de voltaje a través de la resistencia y el inductor se pueden expandir usando la ley de Ohm, usando la corriente de malla original asociada con cada componente.

\[E_1 −E_2 = i_1 R +i_2 jX_L \nonumber \]

Además, por inspección,

\[I_s = i_2 −i_1 \text{ or} \nonumber \]

\[i_2 = i_1 +I_s \nonumber \]

Ahora tenemos dos ecuaciones con dos incógnitas y podemos resolver por\(i_1\) y\(i_2\). Este procedimiento se ilustra en el siguiente ejemplo.

Ejemplo\(\PageIndex{4}\)

Encuentra\(v_b\) para el circuito de Figura\(\PageIndex{13}\). \(E_1 = 20\angle 0^{\circ}\)voltios,\(E_1 = 18\angle 90^{\circ}\) voltios y\(I_S = 10E−3\angle 0^{\circ}\) amperios.

Figura\(\PageIndex{13}\): Circuito por Ejemplo\(\PageIndex{4}\).

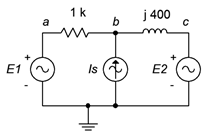
Primero, etiquetamos los bucles, como se muestra en la Figura\(\PageIndex{14}\).

Figura\(\PageIndex{14}\): Circuito de Figura\(\PageIndex{13}\) con supermalla etiquetada.

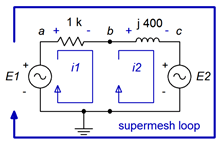
Ahora realizamos una suma KVL alrededor del bucle supermesh.

\[\sum v_{rises} = \sum v_{drops} \nonumber \]

\[20 \angle 0^{\circ} V = v_R+v_{XL}+18\angle 90^{\circ} V \nonumber \]

Expandir usando la ley de Ohm y reorganizar:

\[20 \angle 0^{\circ} V −18\angle 90^{\circ} V = 1k\Omega i_1+j 400 \Omega i_2 \nonumber \]

\[26.9 \angle −42^{\circ} V = 1k\Omega i_1+j 400 \Omega i_2 \nonumber \]

Por inspección podemos ver que:

\[10E-3\angle 0^{\circ} A = i_2 −i_1 \text{ or} \nonumber \]

\[i_2 = i_1 +10E-3\angle 0^{\circ} A \nonumber \]

Podemos sustituir esta expresión en la expresión supermesh anterior y resolver por\(i_1\):

\[26.9 \angle −42^{\circ} V = 1k\Omega i_1 +j 400 \Omega i_2 \nonumber \]

\[26.9 \angle −42^{\circ} V = 1k\Omega i_1+j 400 \Omega (i_1+10E-3 \angle 0^{\circ} A) \nonumber \]

\[26.9 \angle −42^{\circ} V = 1k\Omega i_1+j 400 \Omega i_1+4\angle 90^{\circ} V \nonumber \]

\[29.7\angle −44.7^{\circ} V = (1 k+j 400\Omega )i_1 \nonumber \]

\[i_1 \approx 27.6E-3\angle −69.5^{\circ} A \nonumber \]

Así,\(i_2 = 27.6E−3\angle −69.5^{\circ}\) amperios +\(10E−3\angle 0^{\circ}\) amperios, o\(32.5E−3\angle -52.8^{\circ}\) amperios. Para determinar simplemente\(v_b\) restamos la caída a través de la\(\Omega\) resistencia de 1 k de\(E_1\):

\[v_b = 20 \angle 0^{\circ} V − i_1 1k \Omega \nonumber \]

\[v_b = 20 \angle 0^{\circ} V − 27.6E-3\angle −69.5^{\circ} A1 k\Omega \nonumber \]

\[v_b \approx 27.85\angle 68.2^{\circ} V \nonumber \]

Como comprobación cruzada, también podríamos agregar el voltaje a través del inductor para\(E_2\):

\[v_b = 18\angle 90^{\circ} V +i_2 j 400\Omega \nonumber \]

\[v_b = 18\angle 90^{\circ} V +32.5E-3\angle −52.8^{\circ} A j400 \Omega \nonumber \]

\[v_b \approx 27.85\angle 68.2^{\circ} V \nonumber \]

Comparación de Nodal y Mesh

Habiendo cubierto tanto nodal como malla con cierto detalle, es justo mirar las dos técnicas para medir sus fortalezas y debilidades. En comparación con el análisis ganglionar, el análisis de malla tiene la ventaja de tratar las impedancias más que las admisiones al escribir el sistema de ecuaciones. Además, el método de inspección de malla funciona con fuentes de voltaje, lo que tiende a ser conveniente para muchos circuitos, mientras que el método de inspección nodal requiere fuentes de corriente. En el lado negativo, el conjunto resultante de corrientes de malla requiere un procesamiento adicional para encontrar corrientes de ramificación o voltajes de nodo. En contraste, el análisis nodal produce voltajes de nodo directamente sin procesamiento adicional. La malla también tiene la desventaja de estar limitada a circuitos planos mientras que no existe tal límite para nodal. En última instancia, en lugar de pensar en términos de qué técnica es “mejor” en general, es más eficiente usar la herramienta adecuada para el trabajo en cuestión. Por ejemplo, si un circuito está poblado con fuentes de voltaje, la malla podría ser la ruta más eficiente, especialmente si se desean corrientes específicas. Por otro lado, si se necesita encontrar voltajes en un circuito que contenga numerosas fuentes de corriente, nodal sería más efectivo.