6.4: Fuentes dependientes
- Page ID
- 85810
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Una fuente dependiente es una fuente de corriente o voltaje cuyo valor no es fijo. En cambio, el valor depende de alguna otra corriente o voltaje del circuito. La forma general para el valor de una fuente dependiente es\(N = kM\) donde\(M\) y\(N\) son corrientes y/o voltajes y\(k\) es la constante de proporcionalidad. Por ejemplo, el valor de una fuente de voltaje dependiente puede ser una función de una corriente, por lo que en lugar de que la fuente sea igual a, digamos, 10 voltios, podría ser igual a veinte veces la corriente que pasa a través de una resistencia en particular, o\(v = 20i\).
Hay cuatro posibles fuentes dependientes: Son la fuente de voltaje controlado por voltaje (VCVS), la fuente de corriente controlada por voltaje (VCCS), la fuente de voltaje controlado por corriente (CCVS) y la fuente de corriente controlada por corriente (CCCS). Los parámetros de fuente y control son los mismos tanto para el VCVS como para el CCCS por lo que no\(k\) tiene unidades, aunque se puede dar como voltios/voltio y amps/amp, respectivamente. Para el VCCS y CCVS,\(k\) cuenta con unidades de amperios/voltio y voltios/amp, respectivamente. Estos son referidos como la transresistencia y transconductancia de las fuentes con unidades de ohmios y siemens.
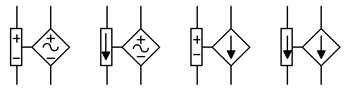
Los símbolos esquemáticos para fuentes dependientes o controladas generalmente se dibujan usando un diamante en lugar de un círculo. También, para los simuladores, habrá una conexión secundaria para la corriente o voltaje de control. En la Figura se muestran ejemplos de fuentes controladas por voltaje y controladas por corriente\(\PageIndex{1}\). En cada uno de estos símbolos, el elemento de control se muestra a la izquierda de la fuente.
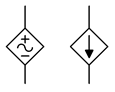
La porción de control se puede considerar como una conexión para un voltímetro o amperímetro que detecta el parámetro de control. Estas conexiones de detección no siempre se dibujan en un esquema. En cambio, la fuente simplemente puede etiquetarse como una función, como en\(v = 0.02 i_X\) dónde\(i_X\) está la corriente controladora. Estas fuentes controladas más simples se muestran en la Figura\(\PageIndex{2}\) y son típicas en esquemas y textos electrónicos. En algunos casos, estas fuentes se dibujan con un círculo en lugar de un diamante. Además, la forma de onda sinusoidal que se muestra aquí a menudo se omite desde el interior del símbolo, sin embargo, las fuentes de corriente siempre se dibujan con una flecha apuntando en la dirección de referencia y las fuentes de voltajes siempre incluyen la polaridad de referencia.
Las fuentes dependientes no son artículos “listos para usar” de la misma manera que lo son una batería o un generador de señal. Más bien, se utilizan fuentes dependientes para modelar el comportamiento de dispositivos más complejos. Por ejemplo, un transistor de unión bipolar se modela comúnmente como un CCCS mientras que un transistor de efecto de campo puede modelarse como un VCCS. Del mismo modo, muchos circuitos amplificadores se modelan como sistemas VCVS. Las soluciones para circuitos que utilizan fuentes dependientes siguen las líneas de las establecidas para fuentes independientes (es decir, la aplicación de la ley de Ohm, KVL, KCL, etc.), sin embargo, las fuentes ahora dependen del resto del circuito lo que tiende a complicar el análisis. En general, existen dos posibles configuraciones de circuito para fuentes dependientes: aisladas y acopladas. Un ejemplo de la forma aislada se muestra en la Figura\(\PageIndex{3}\).
En este ejemplo, la fuente dependiente (centro, un CCVS) no interactúa con el subcircuito de la izquierda impulsado por la fuente independiente\(E\). Así se puede analizar como dos circuitos separados como se muestra en la Figura\(\PageIndex{4}\).
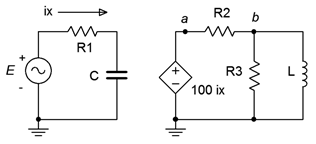
Las soluciones para esta forma son relativamente sencillas. El valor de control para la fuente dependiente se puede calcular directamente utilizando técnicas estándar. Entonces este valor se sustituye en la fuente dependiente y el análisis continúa como normal. A veces es conveniente si la solución para un voltaje o corriente particular se define en términos del parámetro de control en lugar de como un valor específico (por ejemplo, la corriente a través de un componente particular podría ser 75\(i_1\) en lugar de solo 1 miliamperio).
El segundo tipo de circuito (acoplado) es algo más complejo ya que la fuente dependiente puede afectar al parámetro que controla la fuente dependiente. Un ejemplo se muestra en la Figura\(\PageIndex{5}\).
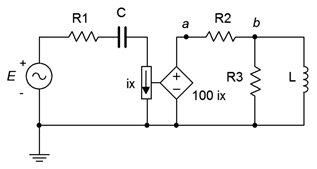
En este ejemplo debería ser obvio que la tensión de la fuente dependiente puede afectar la tensión en el nodo\(a\), y es esta misma tensión la que define\(i_x\), que a su vez establece el valor de la fuente dependiente. En lo que respecta al análisis, se puede utilizar ya sea malla o nodal. La (s) fuente (es) dependiente (es) aportará términos que incluyan el parámetro (s) de control por lo que se requerirá algún esfuerzo adicional. Para ilustrar la técnica, considere el circuito de la Figura\(\PageIndex{6}\). Se utilizará el método general de análisis ganglionar.
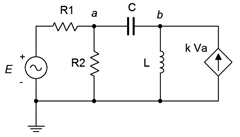
Comenzamos definiendo las direcciones actuales. Supongamos que las corrientes a través\(R_1\) y\(C\) están fluyendo hacia el nodo\(a\), la corriente a través\(R_2\) está fluyendo fuera del nodo\(a\), y la corriente a través\(L\) está fluyendo fuera del nodo\(b\). Numeraremos las corrientes de ramificación para reflejar los componentes asociados, de izquierda a derecha. Las ecuaciones KCL resultantes son:
\[\sum i_{in} = \sum i_{out} \nonumber \]
\[\text{Node } a: i_1 +i_3 = i_2 \nonumber \]
\[\text{Node } b: k v_a = i_3 +i_4 \nonumber \]
Las corrientes son luego descritas por sus equivalentes de ley de Ohm:
\[\text{Node } a: \frac{E−v_a}{R_1} + \frac{v_b−v_a}{− jX_C} = \frac{v_a}{R_2} \nonumber \]
\[\text{Node } b: k v_a = \frac{v_b−v_a}{R_2} + \frac{v_b}{jX_L} \nonumber \]
Expandiendo los rendimientos de términos:
\[\text{Node } a: \frac{E}{R_1} − \frac{v_a}{R_1} + \frac{v_b}{− jX_C} − \frac{v_a}{− jX_C} = \frac{v_a}{R_2} \nonumber \]
\[\text{Node } b: k v_a = \frac{v_b}{R_2} − \frac{v_a}{R_2} + \frac{v_b}{jX_L} \nonumber \]
Recopilación de términos y simplificación de rendimientos:
\[\text{Node } a : \frac{E}{R_1} = \left( \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{− jX_C} \right) v_a − \frac{1}{− jX_C} v_b \nonumber \]
\[\text{Node } b: 0 = − \left( k + \frac{1}{R_2} \right) v_a + \left( \frac{1}{R_2} + \frac{1}{jX_L} \right) v_b \nonumber \]
En este punto, los valores de componente y el valor fuente independiente se insertarían en las ecuaciones y se resolvería el sistema.
Finalmente, remitiéndose al capítulo anterior, es posible realizar conversiones de origen en fuentes dependientes, dentro de límites. La nueva fuente seguirá siendo una fuente dependiente (por ejemplo, VCVS a VCCS). Este proceso no es aplicable si el parámetro de control involucra directamente la impedancia interna (es decir, es su voltaje o corriente).
Ejemplo 6.11
Para el circuito que se muestra en la Figura\(\PageIndex{7}\), determine\(v_c\) si la fuente es pico de\(1\angle 0^{\circ}\) voltios.
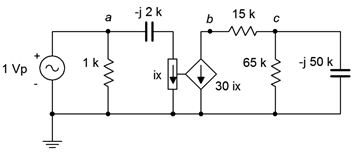
Este es un ejemplo de la fuente dependiente aislada o desacoplada. El valor de la fuente de corriente dependiente es 30 veces el valor de la corriente etiquetada\(i_x\), que es la corriente que fluye a través de la reactancia\(−j2 k\Omega\) capacitiva. Podemos encontrar esta corriente primero y luego determinar el valor resultante de la fuente dependiente. El análisis no requerirá nada más que las técnicas básicas de serie-paralelo. Numeraremos los componentes de izquierda a derecha.
La corriente\(i_x\) se encuentra a través de la ley de Ohm:
\[i_x = \frac{E}{− jX_{C1}} \nonumber \]
\[i_x = \frac{1\angle 0^{\circ} V}{− j 2 k\Omega} \nonumber \]
\[i_x = 0.5E-3\angle 90 ^{\circ} A \nonumber \]
La fuente dependiente es 30 veces este valor, o\(15E−3\angle 90^{\circ}\) amperios. Dada la dirección de referencia de esta fuente, la corriente fluye hacia arriba a través de la\(\Omega\) resistencia de 65 k y el\(−j50 k\Omega\) condensador paralelo. Esto se establece\(v_c\) como negativo. \(i_x\)Al multiplicar por la impedancia paralela se obtiene el voltaje deseado.
\[Z_{RC} = \frac{R_3 \times jX_{C2}}{R_3 − jX_{C2}} \nonumber \]
\[Z_{RC} = \frac{65k \Omega \times (− j50 k \Omega)}{65 k\Omega − j 50 k \Omega} \nonumber \]
\[Z_{RC} = 39.6E3\angle −52.4^{\circ} \Omega \nonumber \]
\[v_c = −i_x \times Z_{RC} \nonumber \]
\[v_c =−15E-3\angle 90^{\circ} \Omega \times 39.6E3\angle −52.4^{\circ} \Omega \nonumber \]
\[v_c = 594\angle −142.4 ^{\circ}V \nonumber \]
El siguiente ejemplo presenta una configuración acoplada resuelta mediante análisis ganglionar.
Ejemplo 6.12
En el circuito de la Figura\(\PageIndex{8}\), determinar\(v_a\). \(E =20\angle 0^{\circ}\)pico de voltios a 50 kHz.
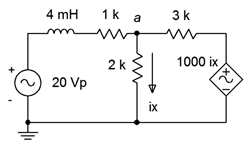
En este circuito tenemos una fuente de voltaje controlado por corriente, o CCVS. La unidad adecuada para la constante de 1000 es ohmios (voltios sobre amperios). Primero, necesitamos determinar el valor de reactancia para el inductor.
\[X_L = 2\pi f L \nonumber \]
\[X_L = 2\pi 50 kHz 4mH \nonumber \]
\[X_L = j 1257\Omega \nonumber \]
Aquí solo hay un nodo de interés (\(a\)) así que solo necesitaremos una ecuación de KCL. El único desconocido es\(v_a\). Supongamos que las direcciones de referencia de las corrientes que fluyen a través de las\(\Omega\) resistencias de 1 k\(\Omega\) y 3 k están entrando al nodo\(a\). A estos los llamaremos\(i_1\) y\(i_2\), respectivamente. La corriente de salida es\(i_x\).
La suma de KCL es:
\[\sum i_{in} = \sum i_{out} \nonumber \]
\[i_1+i_2 = i_x \nonumber \]
Esto se expande usando la ley de Ohm (en varios pasos, para mayor claridad).
\[i_x = i_1+i_2 \nonumber \]
\[\frac{v_a}{R_2} = \frac{E −v_a}{R_1+jX_L} + \frac{1000(\Omega)i_x−v_a}{R_3} \nonumber \]
\[\frac{v_a}{2 k\Omega} = \frac{20\angle 0^{\circ} V−v_a}{1k+j 1257\Omega} + \frac{1000 (\Omega)i_x−v_a}{3k \Omega} \nonumber \]
\[\frac{20\angle 0^{\circ} V}{1 k+j 1257\Omega} = \frac{v_a}{1k+j 1257\Omega} + \frac{v_a}{2k \Omega} + \frac{v_a}{3k \Omega} − \frac{1000(\Omega)i_x}{3k \Omega} \nonumber \]
\[12.45\angle −51.5^{\circ} A = \frac{v_a}{1k+j 1257\Omega} + \frac{v_a}{2 k\Omega} + \frac{v_a}{3k \Omega} − \frac{1000(\Omega) v_a}{2k \Omega \times 3k \Omega} \nonumber \]
\[12.45\angle −51.5^{\circ} A = \frac{v_a}{1k+j 1257\Omega} + \frac{v_a}{2k \Omega} + \frac{v_a}{3k\Omega} − \frac{v_a}{6k \Omega} \nonumber \]
\[12.45\angle −51.5^{\circ} A = \left( \frac{1}{1 k+j1257\Omega} + \frac{1}{2 k\Omega} + \frac{1}{3k \Omega} − \frac{1}{6 k\Omega} \right) v_a \nonumber \]
\[12.45\angle −51.5^{\circ} A = 1.161E-3\angle −24.8^{\circ} S v_a \nonumber \]
\[v_a = 10.7 \angle −26.7^{\circ} V \nonumber \]
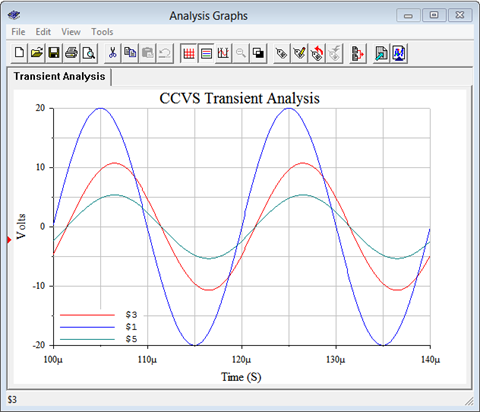
Simulación por Computadora
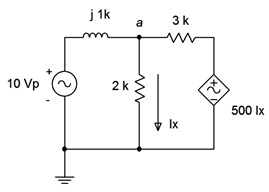
Para la verificación, el circuito fuente dependiente de Ejemplo\(\PageIndex{2}\) se ingresa en un simulador como se muestra en la Figura\(\PageIndex{9}\). Los resultados se muestran en la Figura\(\PageIndex{10}\).
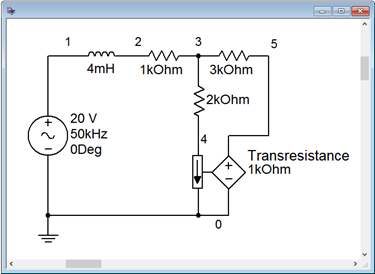
Anote la conexión para detectar la corriente\(i_x\). Se inserta igual que un amperímetro. Como se mencionó anteriormente, la constante para la fuente dependiente es una transresistencia y tiene unidades de ohmios. Se ejecuta un análisis transitorio en el circuito, trazando la fuente independiente\(E\),, como nodo 1 (azul), y\(v_a\) como nodo 3 (rojo). Tanto la amplitud como el desplazamiento de fase retrasado se alinean muy bien con el resultado calculado. El voltaje de la fuente dependiente también se representa como nodo 5 (verde). Verificar este potencial se deja como ejercicio.