6.4: Formación de Solitones Manejados por

La ecuación no lineal de Schrödinger describe la propagación de pulsos en un medio con dispersión continuamente distribuida y auto-modulación de fase. Para los láseres que generan pulsos tan cortos como 10 fs e inferiores, Spielmann et al. señalaron primero que grandes cambios en el pulso ocurren dentro de un viaje de ida y vuelta y que el orden de los elementos de conformación de pulso dentro de la cavidad tiene un efecto mayor en la formación del pulso [9]. La acción discreta de la dispersión lineal en los brazos del resonador láser y la acción discreta, pero simultánea, de SPM positivo y GDD positivo en el cristal láser ya no se pueden descuidar. La importancia de las fuertes variaciones de dispersión para la dinámica del láser se descubrió por primera vez en un láser de fibra y se llamó modelocking de pulso estirado [11]. La dispersión positiva en la sección de fibra dopada con ER de un láser de anillo de fibra se equilibró con una fibra pasiva dispersiva negativa. El pulso que circulaba en el anillo se estiró y comprimió hasta en un factor de 20 en una ida y vuelta. Una consecuencia de este comportamiento fue una disminución dramática de la no linealidad y, por lo tanto, aumentó la estabilidad frente a las inestabilidades inducidas por SPM. Las bandas laterales, debido a perturbaciones periódicas del solitón, como se discute en la sección 3.6, ya no se observan (ver Figura 6.12).

Imagen eliminada debido a restricciones de derechos de autor.

Por favor, vea:
Tamura, K., E. P. Ippen, H. A. Haus, y L. E. Nelson. “Generación de pulsos de 77-fs a partir de un láser de anillo de fibra totalmente bloqueado en modo de pulso estirado”. Letras Ópticas 18 (1993): 1080-1082.

Figura 6.12: Espectros de láseres de fibra dopados con ER de modo bloqueado que operan en el régimen de solitón convencional, es decir, dispersión negativa neta y en el modo de operación de pulso estirado a dispersión promedio casi nula [11].

La energía de los pulsos de salida podría incrementarse 100 veces. El ancho de pulso mínimo fue 63 fs, con un ancho de banda mucho más amplio que el ancho de banda de ganancia de erbio [12]. La Figura 6.12 también muestra la mejora espectral del láser de fibra en el régimen de dispersión manejada. La generación de pulsos ultracortos a partir de láseres de estado sólido como Ti:zafiro ha progresado en la última década y condujo a la generación de pulsos tan cortos como 5 fs directamente desde el láser. A longitudes de pulso tan cortas el pulso se estira hasta un factor de diez cuando se propaga a través del cristal láser creando un solitón manejado por dispersión [10]. Los espectros generados con estos láseres no son de forma sencilla por muchas razones. Aquí, queremos considerar el impacto en la forma espectral y la dinamcis láser debido a la formación de solitones gestionados por dispersión.

Figura 6.13: (a) Esquema de un láser Ti:zafiro bloqueado en modo Kerr-lens: P's, prismas; L, lente; DCM, espejo de doble chirped; TiSA, Ti:zafiro. b) Correspondencia con transmisión de fibra gestionada por dispersión.

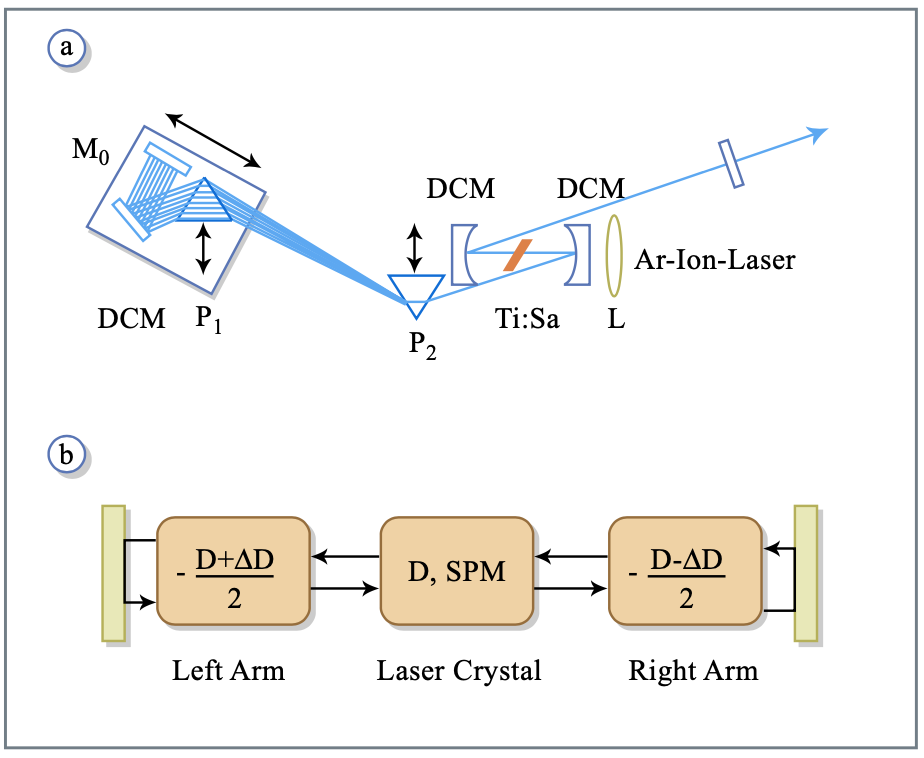
Figura por MIT OCW.

Un láser de modo bloqueado que produce pulsos ultracortos consiste al menos en pares de prismas de ganancia), ver Figura 6.13 a. El sistema puede descomponerse en los brazos de res- onador y el cristal, ver Figura 6.13 b. Para lograr pulsos ultracortos, los componentes de equilibrio de dispersión deben producir dispersión neta cercana a cero mientras que el (los) elemento (s) de dispersión produce individualmente un retardo de grupo significativo sobre el ancho de banda amplio del pulso láser. Este hecho sugiere una analogía con la propagación de pulsos gestionada por dispersión a lo largo de un enlace de transmisión de fibra gestionada por dispersión [14]. Un sistema con suficiente variación de dispersión puede soportar ondas solitarias. Se puede demostrar que la no linealidad de Kerr produce un potencial de dispersión no lineal autoconsistente que permite la formación de una solución peródica con un factor de fase simple en un sistema con dispersión neta cero. Los pulsos son análogos a los solitones en que son soluciones autoconsistentes del problema hamiltoniano (sin pérdida) como los solitones convencionales discutidos anteriormente. Pero no son secantes hiperbólicos en forma. La Figura 6.14 muestra una simulación numérica de una solución autoconsistente del problema de propagación de pulsos hamiltonianos en un medio lineal de dispersión negativa y posterior propagación en un medio no lineal de dispersión positiva y modulación de autofase positiva, siguiendo la ecuación

\[\dfrac{\partial}{\partial z} A(z, t) = j D(z) \dfrac{\partial^2}{\partial t^2} A(z, t) - j \delta (z) |A|^2 A(z, t)\label{eq6.4.1} \]

Imagen eliminada debido a restricciones de derechos de autor. Por favor vea:

Chen, Y., et al. “Bloqueo de modo gestionado por dispersión”. Revista de la Sociedad Óptica de las Américas B 16 (1999): 1999-2004.

Figura 6.14: Conformación de pulsos en un viaje de ida y vuelta. El segmento negativo no tiene no linealidad.

En la Figura 6.15 se muestran los perfiles de intensidad en estado estacionario en el centro del segmento de dispersión negativa en 1000 viajes de ida y vuelta. Es claro que la solución se repite de periodo a periodo, es decir, hay una nueva onda solitaria que resuelve la ecuación de Schroedinger no lineal por tramos 6.65, solitón manejado por dispersión. En contraste con el solitón convencional, el solitón mangaged dispersión de la ecuación 6.65 (sin SAM y sin filtrado) se asemejan a pulsos gaussianos hasta aproximadamente -10 dB desde el pico, pero luego muestran una estructura bastante complicada, ver Figura 6.15.El mapa de dispersión\(D(z)\) utilizado se muestra como un recuadro en la Figura 6.14. Uno puede incluir adicionalmente ganancia saturable, filtración de ganancia lorentziana y un absorbedor saturable rápido. La Figura 6.14 muestra el comportamiento en un periodo (un viaje de ida y vuelta a través del resonador) incluyendo estos efectos. La respuesta del absorbedor es\(q(A) = q_o/(1+|A|^2/P_A)\), con\(q_o = 0.01\) /mm y\(P_A = 1\) MW. La ganancia limitada de ancho de banda es modelada por el perfil de Lorentzian con ancho de banda de ganancia\(2\pi \times 43\) ThZ. El filtrado y la absorción saturable reducen los lóbulos laterales espectrales y temporales del problema hamiltoniano. Como puede deducirse de la Figura 6.14, la formación de impulsos de estado estacionario se puede entender de la siguiente manera. Por simetría, los pulsos están libres de chirp en el medio de las células de dispersión. Un pulso libre de chirp que comienza en el centro del cristal de ganancia, es decir, un segmento no lineal es ensanchado espectralmente por el SPM y se dispersa en el tiempo debido al GVD, lo que genera un chirp bastante lineal sobre el pulso. Después de que el pulso está saliendo del cristal experimenta GVD negativo durante la propagación a través del brazo resonador izquierdo o derecho, que está comprimiendo el pulso con chirrido positivo hasta su límite de transformación al final del brazo, donde se puede colocar un acoplador de salida. La retropropagación hacia el cristal impone un chirp negativo, generando la solución de tiempo invertido de la ecuación de Schrödinger no liner (\(\ref{eq6.4.1}\)). Por lo tanto, la propagación posterior en el cristal no lineal está comprimiendo el pulso espectral y temporalmente a su forma inicial en el centro del cristal. El espectro es más estrecho en el cristal que en las secciones de dispersión negativa, debido a que es prechirpeado negativamente antes de que entre en la sección SPM y la dispersión espectral se produce nuevamente solo después de que el pulso haya sido comprimido. Este resultado explica además que en un láser con una cavidad lineal, para el cual la dispersión negativa se ubica en un solo brazo del resonador láser (es decir, en el par prismático y sin uso de espejos gorjeados) el espectro es más ancho en el brazo que contiene la dispersión negativa. En un láser con una cavidad lineal, para el cual la dispersión negativa se distribuye equitativamente en ambos brazos de la cavidad, el pulso recorre el mapa de dispersión dos veces por ida y vuelta. El pulso es corto en cada extremo de la cavidad y, lo más importante, los pulsos son idénticos en cada paso a través del cristal, lo que explota la acción absorbente saturable (Kerr-Lens Modelocking en este caso, como se discutirá en el siguiente capítulo) dos veces por ida y vuelta, en contraste con una dispersión asimétrica distribución en los brazos del resonador. Por lo tanto, una distribución de dispersión simétrica conduce a una absorción saturable efectiva que es dos veces más fuerte que una distribución de dispersión asimétrica que resulta en pulsos sustancialmente más cortos. Además, la oscilación de dispersión entre las secciones de dispersión negativa y positiva es solo la mitad, lo que permite solitones manejados por dispersión más cortos que operan al mismo nivel de potencia promedio.

Imagen eliminada debido a restricciones de derechos de autor. Por favor vea:

Chen, Y., et al. “Bloqueo de modo gestionado por dispersión”. Revista de la Sociedad Óptica de las Américas B 16 (1999): 1999-2004.

Figura 6.15: Simulación del problema hamiltoniano. Los perfiles de intensidad en el centro del segmento dispersivo negativo se muestran para viajes sucesivos de ida y vuelta. La extensión total en 1000 viajes de ida y vuelta. \(D = D^{(\pm)} = \pm 60\ fs^2/mm\), segmento de cristal longitud\(L = 2\) mm,\(\tau_{FWHM} = 5.5\) fs,\(\delta = 0\) para\(D < 0\),\(\delta = 1\ (MW\ mm)^{-1}\) para\(D > 0\). [10]

Para ilustrar mejor la eficiencia de la formación de solitones manejados por dispersión, presentamos una serie de simulaciones que comienzan con un segmento lineal de dispersión negativa y un segmento no lineal de dispersión positiva de la misma magnitud, acción absorbente saturable y filtrado.

Imagen eliminada debido a restricciones de derechos de autor. Por favor vea:

Chen, Y., et al. “Bloqueo de modo gestionado por dispersión”. Revista de la Sociedad Óptica de las Américas B 16 (1999): 1999-2004.

Figura 6.16: Secuencia de perfiles de pulso en el centro del segmento negativo dispersivo para tres magnitudes de SPM. \(t_o = 3\ fs\), con curvas sólidas (5.5 fs) para\(\delta = 1\ (MW\ mm)^{-1}\), curva discontinua y punteada (7 fs) para\(\delta = 0.5 \ (MW\ mm)^{-1}\), y cuves discontinuas para ningún SPM de\(\delta = 0\). El mapa de dispersión es de la Figura 6.14. La pérdida del acoplador de salida es de 3%. [10]

La curva discontinua de la Figura 6.16 muestra la forma del pulso para ganancia, pérdida, absorción saturable y filtrado de ganancia solamente. Obtuvimos las otras trazas incrementando el SPM manteniendo la energía fija a través del ajuste de la ganancia. Como se puede ver, aumentar el SPM permite pulsos más cortos. El pulso más corto puede ser aproximadamente tres veces más corto que el pulso sin SPM. Los parámetros elegidos para las simulaciones se enumeran en la leyenda de la figura. En este sentido, el comportamiento es similar al caso del absorbedor saturable rápido con formación convencional de solitones como se discutió en la última sección.

Una diferencia importante en el caso del solitón manejado por dispersión se ilustra en la Figura 6.17. La figura muestra los rangos de parámetros para un sistema de solitón administrado por dispersión (sin ganancia, sin pérdida, sin filtrado) que está desequilibrado para dar como resultado la dispersión neta que sirve como abscisa de la figura. Cada curva da el lugar de la energía frente a la dispersión de la cavidad neta para una relación de estiramiento\(S = LD/\tau_{FWHM}^2\) (o ancho de pulso con longitud de cristal fija\(L\)). Se puede ver que para un ancho de pulso mayor a 8 fs con longitud de cristal\(L = 2\ mm\), no existe solución de energía finita en el sistema gestionado por dispersión para dispersión neta cero o positiva. Los pulsos de duraciones superiores a 8 fs requieren dispersión neta negativa. Por lo tanto, se puede alcanzar la operación de soliton manejada por dispersión ultracorta a dispersión neta cero solo proporcionando primero al sistema una dispersión negativa. A la misma energía, se puede formar un pulso más corto reduciendo la dispersión neta, siempre que se haya superado el umbral de 8 fs. Para una oscilación de dispersión fija\(\pm D\), el estiramiento aumenta cuadráticamente con el ancho espectral o el ancho de pulso inverso. Los pulsos largos sin estiramiento tienen forma sech. Para relaciones de estiramiento de 3-10 los pulsos son de forma gaussiana. Para relaciones de estiramiento aún mayores, los espectros de pulso se vuelven cada vez más planos rematados, como se muestra en la Figura 6.16.

Imagen eliminada debido a restricciones de derechos de autor. Por favor vea:

Chen, Y., et al. “Bloqueo de modo gestionado por dispersión”. Revista de la Sociedad Óptica de las Américas B 16 (1999): 1999-2004.

Figura 6.17: Energía del pulso en el sistema gestionado por dispersión sin pérdidas con estiramiento\(S = LD/\tau_{FWHM}^2\) o para una longitud de cristal fija\(L\) y ancho de pulso como parámetros;\(D = 60\ fs^2/mm\) para Ti:zafiro a 800 nm [10].

Para conocer la dinámica del láser y posteriormente en su comportamiento de ruido y afinación, es ventajoso formular también un enfoque de ecuación maestra para el caso de solitón manejado por dispersión [16]. Hay que tener cuidado de que el desplazamiento de fase Kerr-sea producido por un pulso de amplitud y anchura variables a medida que circula alrededor del anillo. El desplazamiento de fase Kerr-para un pulso de ancho constante,\(\delta |a|^2\) tuvo que ser reemplazado por un perfil de fase que imita la forma promedio del pulso, ponderada por su intensidad. Por lo tanto, la acción SPM se sustituye por

\[\delta |A|^2 = \delta_o |A_o|^2 \left ( 1 - \mu \dfrac{t^2}{\tau^2} \right ) \nonumber \]

donde\(A_o\) está la amplitud del pulso en la posición de ancho mínimo. El perfil de fase Kerrse expande a segundo orden en\(t\). El coeficiente\(\delta_o\) y\(\mu\) se evalúan variacionalmente. La acción absorbente saturable se expande de manera similar. Finalmente, la dispersión neta intracavitaria que actúa en promedio sobre el pulso es reemplazada por la dispersión efectiva\(D_{\text{net}}\) en el resonador dentro de una ida y vuelta. La ecuación maestra se convierte

\[T_R \dfrac{\partial}{\partial T} A = (g - l) A + \left (\dfrac{1}{\Omega_f^2} + j D_{\text{net}} \right ) \dfrac{\partial^2}{\partial t^2} A + (\gamma_o - j \delta_o) |A_o|^2 \left (1 - \mu \tfrac{t^2}{\tau^2} \right ) A\label{eq6.4.3} \]

Esta ecuación tiene soluciones de pulso gaussiano. La ecuación maestra (\(\ref{eq6.4.3}\)) es un mosaico, no es una ecuación diferencial ordinaria. Los coeficientes en la ecuación dependen de la solución del pulso y eventualmente tienen que ser encontrados iterativamente. Sin embargo, la ecuación da cuenta de la conformación del pulso en el sistema de manera analítica. Permitirá extender la teoría convencional de perturbación de solitones al caso de solitones manejados por dispersión.

Hay una propiedad más interesante de la operación de pulso estirado que hay que enfatizar. Los solitones manejados por dispersión pueden formarse incluso cuando la dispersión neta observada por un pulso de propagación lineal es cero o ligeramente positiva. Este es un resultado sorprendente el cual fue descubierto en el estudio de propagación de solitones manejados por dispersión [14]. Resulta que el pulso estirado cambia su espectro durante la propagación a través de los dos segmentos de fibra con dispersión opuesta o en el caso de un láser Ti:Sapphire en el cristal no lineal. El espectro en el segmento con dispersión normal (positiva) es más estrecho, que en el segmento de dispersión anómala (nega- tiva), ver Figura 6.14. El pulso ve una dispersión neta negativa efectiva, siempre que el positivo no\(D_{\text{net}}\) sea demasiado grande. En (\(\ref{eq6.4.3}\)) el\(D_{\text{net}}\) es a ser reemplazado por el\(D_{\text{eff}}\) cual se puede computar variacionalmente. Por lo tanto, las soluciones similares a solitones gestionadas por dispersión pueden existir incluso cuando\(D_{\text{net}}\) es cero. Sin embargo, solo existen si el factor de estiramiento es grande, ver Figura 6.17.

Una propiedad notable de los solitones manejados por dispersión es que no irradian (generan continuo) a pesar de que se propagan en un medio con cambios bruscos de dispersión. Esto se puede entender por el hecho de que el solitón mangaseado de dispersión es una solución de la dinámica de base incorporando ya las variaciones de dispersión periódicas incluyendo el efecto Kerr-effect. Esto contrasta con el solitón en un ambiente dispersivo distribuido continuamente, donde las variaciones periódicas en la dispersión y la no linealidad conducen a la radiación.

Bibliografía

[1] G.H.C. Nuevo: “Evolución del pulso en láseres cuasicontinuos de modo bloqueado”, IEEE J. Quantum Electron. 10, 115-124 (1974)

[2] H. A. Haus,” Teoría del bloqueo de modo con un absorbedor saturable lento”, IEEE J. Quantum Electron. 11, pp. 736 — 746 (1975).

[3] H. A. Haus,” Teoría del modelocking con un absorbedor saturable rápido”, J. Appl. Phys. 46, pp. 3049 — 3058 (1975).

[4] H. A. Haus, J. G. Fujimoto, E. P. Ippen,” Estructuras para modebloqueo de pulso aditivo”, J. Opt. Soc. de Am. B 8, pp. 2068 — 2076 (1991).

[5] E. P. Ippen,” Principios de bloqueo en modo pasivo”, Appl. Phys. B 58, pp. 159 — 170 (1994).

[6] F. X. Kärtner y U. Keller,” Estabilización de pulsos similares a solitones con un absorbedor saturable lento”, Opt. Lett. 20, 16 — 19 (1995).

[7] F.X. Kärtner, I.D. Jung, U. Keller: TÍTULO, “Soliton Modelocking with Saturable Absorbers”, Número Especial sobre Electrónica Ultrafrápida, Fotónica y Optoelectrónica, IEEE J. Sel. Parte superior. Electrón cuántico. 2, 540-556 (1996)

[8] I. D. Jung, F. X. Kärtner, L. R. Brovelli, M. Kamp, U. Keller,” Verificación exper- imental del modebloqueo de soliton utilizando únicamente un absorbedor saturable lento,” Opt. Lett. 20, pp. 1892 — 1894 (1995).

[9] C. Spielmann, P.F. Curley, T. Brabec, F. Krausz: Láseres fem- a segundo de banda ultracircular, IEEE J. Quantum Electron. 30, 1100-1114 (1994).

[10] Y. Chen, F. X. Kärtner, U. Morgner, S. H. Cho, H. A. Haus, J. G. Fujimoto, y E. P. Ippen, “Bloqueo de modo gestionado por dispersión”, J. Opt. Soc. Am. B 16, 1999-2004, 1999.

[11] K. Tamura, E.P. Ippen, H.A. Haus, L.E. Nelson: generación de pulsos de 77-fs a partir de un láser de anillo de fibra con bloqueo de modo de pulso estirado, Opt. Lett. 18, 1080-1082 (1993)

[12] K. Tamura, E.P. Ippen, H.A. Haus: Dinámica de pulso en láseres de pulso estirado, Appl. Phys. Lett. 67, 158-160 (1995)

[13] F.X. Kärtner, J. A. d. Au, U. Keller, “Modo-bloqueo con absorbedores saturables lentos y rápidos-Cuál es la diferencia”,. Sel. Parte superior. Electrón cuántico. 4, 159 (1998)

[14] J.H.B. Nijhof, N.J. Doran, W. Forysiak, F.M. Knox: Sistema estable manejado por indispersión de propagación similar al solitón con dispersión anómala neta, cero y nromal, Electron. Lett. 33, 1726-1727 (1997)

[15] Y. Chen, H.A. Haus: Solitones manejados por dispersión en el régimen de dispersión neta positiva, J. Opt. Soc. Am. B 16, 24-30 (1999)

[16] H.A. Haus, K. Tamura, L.E. Nelson, E.P. Ippen, “Modeo de pulso ad- ditivo de pulso estirado en láseres de anillo de fibra: teoría y experimento”, IEEE J. Quantum Electron. 31, 591-598 (1995)

[17] I. D. Jung, F. X. Kärtner, N. Matuschek, D. H. Sutter, F. Morier- Genoud, Z. Shi, V. Scheuer, M. Tilsch, T. Tschudi, U. Keller,” Espejos absorbedores saturables semicono-ductores que soportan pulsos sub-10 fs,” Appl. Phys. B 65, pp. 137-150 (1997).