11.4: Mezcla de Cuatro Ondas

Una técnica de espectroscopía ultrarrápida más avanzada que la bomba-sonda es la mezcla de cuatro ondas (FWM). Permite investigar no solo los procesos de relajación energética, como es el caso en las mediciones de bomba-sonda, sino también los procesos de desfase en materiales homogéneos y no homogéneamente ampliados. La configuración típica se muestra en la Figura 11.12

Figura 11.12: Geometría típica de haz de mezcla de cuatro ondas (FWM).

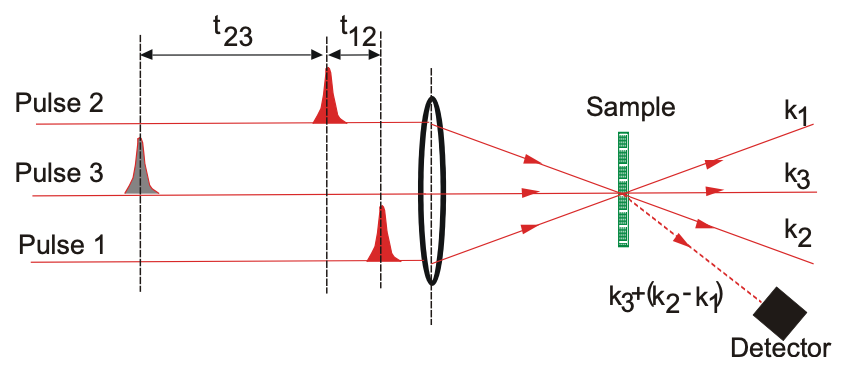
Supongamos que estos pulsos interactúan resonante con un sistema de dos niveles modelado por las Ecuaciones de Bloch derivadas en el capítulo 2 (2.1592.162).

\[\left (\Delta - \dfrac{1}{c_0^2} \dfrac{\partial^2}{\partial t^2} \right ) \vec{E}^{(+)} (z, t) = \mu_0 \dfrac{\partial^2}{\partial t^2} \vec{P}^{(+)} (z, t), \nonumber \]

\[\vec{P}^{(+)} (z, t) = -2N \vec{M}^* d(z, t) \nonumber \]

\[\dot{d} (z, t) = -(\dfrac{1}{T_2} - j \omega_{eg})d + \dfrac{1}{2j \hbar} \vec{M} \vec{E}^{(+)} w, \nonumber \]

\[\dot{w} (z, t) = -\dfrac{w - w_0}{T_1} + \dfrac{1}{j \hbar} (\vec{M}^* \vec{E}^{(-)} d - \vec{M} \vec{E}^{(+)} d^*) \nonumber \]

El sistema de dos niveles, ubicado en\(z = 0\), estará en el estado fundamental, es decir,\(d(t = 0) = 0\) y\(w(t = 0) = -1\), antes de la llegada de los primeros pulsos. Es decir, aún no hay polarización presente. Supongamos que el pulso que interactúa con el sistema de dos niveles es débil y podemos aplicar la teoría de la perturbación. Luego la llegada del primer pulso con el campo complejo

\[\vec{E}^{(+)} (\vec{x}, t) = \vec{E}_0^{(+)} \delta (t) e^{j(\omega_{eg} t - j \vec{k}_1 \vec{x})} \nonumber \]

generará una onda de polarización de acuerdo con las ecuaciones Bloch

\[d(\vec{x}, t) = -\dfrac{\vec{M} \vec{E}_0^{(+)}}{2j \hbar} e^{j(\omega_{eg} - 1/T_2)t} e^{-j \vec{k}_1 \vec{x}} \delta (z), \nonumber \]

que decairá con el tiempo. Una vez que se crea una polarización, el segundo pulso cambiará la población e inducirá una red poblacional débil

\[\Delta w(\vec{x}, t) = \dfrac{|\vec{M} \vec{E}_0^{(+)}|^2}{\hbar^2} e^{-t_{12}/T_2} e^{-j(\vec{k}_1 - \vec{k}_2)\vec{x}} e^{-(t - t_2)/T_1} \delta (z) + c.c., \nonumber \]

Cuando llegue el tercer pulso, se dispersará de esta rejilla poblacional, es decir, inducirá una polarización, que irradia una onda en la dirección de\(\vec{k}_3 + \vec{k}_2 - \vec{k}_1\) acuerdo con

\[d (\vec{x}, t) = \dfrac{\vec{M} \vec{E}_0^{(+)}}{2j \hbar} \dfrac{|\vec{M} \vec{E}_0^{(+)}|^2}{\hbar^2} e^{-t_{12}/T_2} e^{-t_{32}/T_1} e^{-j(\vec{k}_3 + \vec{k}_2 - \vec{k}_1)\vec{x}} \delta (z) \nonumber \]

Así la señal detectada en esta dirección, ver Figura 11.12, que es proporcional al cuadrado de la capa dipolo radiante

\[S(t) \sim |d(\vec{x}, t)|^2 \sim e^{-2t_{12}/T_2} e^{-2t_{32}/T_1} \nonumber \]

decaerá en dos escalas de tiempo. Si el retardo de tiempo entre los pulsos 1 y 2\(t_{12}\),, solo se varía, decaerá con el tiempo de desfase\(T_2/2\). Si se varía el retardo de tiempo entre los pulsos 2 y 3\(t_{32}\), la intensidad de la señal decairá con el tiempo de relajación de energía\(T_1/2\)

Bibliografía

[1] K. L. Hall, G. Lenz, E. P. Ippen, y G. Raybon, “Heterodyne pump- probe technique for time-domain studies of optical nonlinearities in waveguides”, Opt. Let. 17, p.874-876, (1992).

[2] K. L. Hall, A. M. Darwish, E. P. Ippen, U. Koren y G. Raybon, “Fem- a segundo índice no linealidades en amplificadores ópticos IngaASP”, App. Phys. Let. 62, p.1320-1322, (1993).

[3] K. L. Hall, G. Lenz, A. M. Darwish, E. P. Ippen, “Ganancia de subpicosegundo y no linealidades de índice en láseres de diodo IngaASP”, Opt. Comm. 111, p.589-612 (1994).

[4] J. A. Valdmanis, G. Mourou, y C. W. Gabel, “Sistema de muestreo electroóptico de picosegundos”, Appl. Phys. Let. 41, p. 211-212 (1982).

[5] B. H. Kolner y D. M. Bloom, “Muestreo electroóptico en circuitos integrados de GaAs”, IEEE J. Quantum Elect.22, 79-93 (1986).

[6] S. Gupta, M. Y. Frankel, J. A. Valdmanis, J. F. Whitaker, G. A. Mourou, F. W. Smith y A. R. Calaw, “Vida útil del portador de subpicosegundos en GaAs cultivados por epitaxia de haz molecular a bajas temperaturas”, App. Phys. Let. 59, pp. 3276-3278 91991)

[7] Ch. Fattinger, D. Grischkowsky, “Vigas de terahercios”, Appl. Phys. Let. 54, pp.490-492 (1989)

[8] D. M. Mittleman, R. H. Jacobsen, y M. Nuss, “T-Ray Imaging”, IEEE JSTQE 2, 679-698 (1996)

[9] A. Bonvalet, J. Nagle, V. Berger, A. Migus, JL Martin y M. Joffre, “Ultrafast Dynamic Control of Spin and Charge Density Oscilations in a GaAs Quantum Well”, Phys. Rev. Let. 76, 4392 (1996).