6.6: Ejercicios
- Page ID
- 85790
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Análisis
(Todos los valores de fuente están en amperios o voltios a menos que se especifique lo contrario
1. Dado el circuito en la Figura\(\PageIndex{1}\), utilizar el análisis nodal para determinar\(v_c\). \(I_1 = 3\angle 0^{\circ}\),\(I_2 = 0.9\angle 0^{\circ}\).
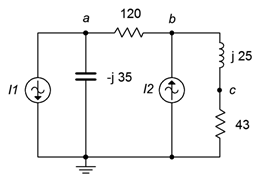
Figura\(\PageIndex{1}\)
2. Utilice el análisis nodal para encontrar la corriente a través de la\(\Omega\) resistencia 120 en el circuito de la Figura\(\PageIndex{2}\). \(I_1 = 0.5\angle 90^{\circ}\),\(I_2 = 1.6\angle 0^{\circ}\).
3. Utilice el análisis nodal para encontrar la corriente a través de la\(\Omega\) resistencia 43 en el circuito de la Figura\(\PageIndex{2}\). Las fuentes están en fase.
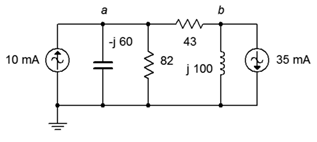
Figura\(\PageIndex{2}\)
4. Dado el circuito en la Figura\(\PageIndex{2}\), utilizar el análisis nodal para determinar\(v_b\). Las fuentes están en fase.
5. Dado el circuito de la Figura\(\PageIndex{3}\), determinar\(v_c\). \(I_1 = 3\angle 0^{\circ}\),\(I_2 = 2\angle 0^{\circ}\).
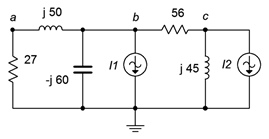
Figura\(\PageIndex{3}\)
6. Utilice el análisis nodal para encontrar la corriente a través del\(j45 \Omega\) inductor en el circuito de la Figura\(\PageIndex{3}\). \(I_1 = 2\angle 0^{\circ}\),\(I_2 = 1.5\angle 60^{\circ}\).
7. Utilice el análisis nodal para encontrar la corriente a través de la\(\Omega\) resistencia 4 en el circuito de la Figura\(\PageIndex{4}\). \(I_1 = 1\angle 45^{\circ}\),\(I_2 = 2\angle 45^{\circ}\).
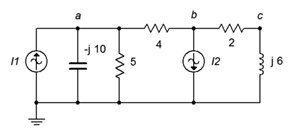
Figura\(\PageIndex{4}\)
8. Dado el circuito en la Figura\(\PageIndex{4}\), utilizar el análisis nodal para determinar\(v_c\). \(I_1 = 6\angle 30^{\circ}\),\(I_2 = 4\angle 0^{\circ}\).
9. Dado el circuito en la Figura\(\PageIndex{5}\), utilizar el análisis nodal para determinar\(v_{ac}\). \(I_1 = 10\angle 0^{\circ}\),\(I_2 = 6\angle 0^{\circ}\).
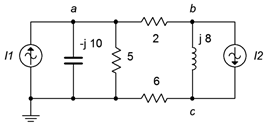
Figura\(\PageIndex{5}\)
10. Utilice el análisis nodal para encontrar la corriente a través del\(j8 \Omega\) inductor en el circuito de la Figura\(\PageIndex{5}\). \(I_1 = 3\angle 0^{\circ}\),\(I2 = 5\angle 30^{\circ}\).
11. Utilice el análisis nodal para encontrar la corriente a través de la\(\Omega\) resistencia 22 en el circuito de la Figura\(\PageIndex{6}\). \(I_1 = 800E−3\angle 0^{\circ}\),\(I_2 = 2.5\angle 0^{\circ}\),\(I_3 = 2\angle 20^{\circ}\).
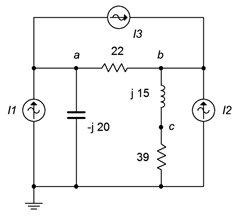
Figura\(\PageIndex{6}\)
12. Dado el circuito en la Figura\(\PageIndex{6}\), utilizar el análisis nodal para determinar\(v_c\). \(I_1 = 4\angle 90^{\circ}\),\(I_2 = 10\angle 120^{\circ}\),\(I_3 = 5\angle 0^{\circ}\).
13. Dado el circuito en la Figura\(\PageIndex{7}\), utilizar el análisis nodal para determinar\(v_c\). \(I_1 = 3E−3\angle 0^{\circ}\),\(I_2 = 10E−3\angle 0^{\circ}\),\(I_3 = 2E−3\angle 0^{\circ}\).
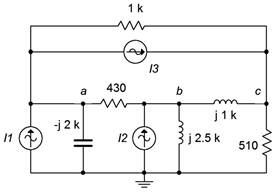
Figura\(\PageIndex{7}\)
14. Utilice el análisis nodal para encontrar la corriente a través del\(\Omega\) condensador\(−j2\) k en el circuito de la Figura\(\PageIndex{7}\). \(I_1 = 1E−3\angle 0^{\circ}\),\(I_2 = 5E−3\angle 0^{\circ}\),\(I_3 = 6E−3\angle −90^{\circ}\).
15. Utilice el análisis nodal para encontrar la corriente a través de la\(\Omega\) resistencia de 3.3 k en el circuito de la Figura\(\PageIndex{8}\). \(E = 36\angle 0^{\circ}\),\(I = 4E−3\angle −120^{\circ}\).
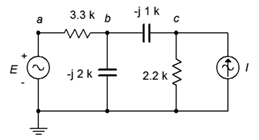
Figura\(\PageIndex{8}\)
16. Dado el circuito de la Figura\(\PageIndex{8}\), escribir las ecuaciones de nodo y determinar\(v_c\). \(E = 18\angle 0^{\circ}\),\(I = 7.5E−3\angle −30^{\circ}\).
17. Dado el circuito en la Figura\(\PageIndex{9}\), utilizar el análisis nodal para determinar\(v_c\). \(E = 40\angle 180^{\circ}\),\(I = 20E−3\angle 0^{\circ}\).
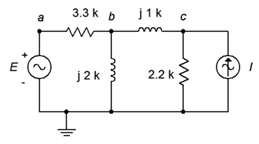
Figura\(\PageIndex{9}\)
18. Utilice el análisis nodal para encontrar la corriente a través de la\(\Omega\) resistencia de 2.2 k en la Figura\(\PageIndex{9}\). \(E = 240\angle 0^{\circ}\),\(I = 100E−3\angle 0^{\circ}\).
19. Utilice el análisis nodal para encontrar\(v_{bc}\) en el circuito de la Figura\(\PageIndex{10}\).
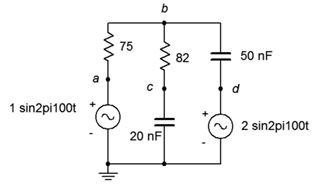
Figura\(\PageIndex{10}\)
20. Utilice el análisis nodal para encontrar la corriente a través de la\(\Omega\) resistencia de 2.7 k en el circuito de la Figura\(\PageIndex{11}\).
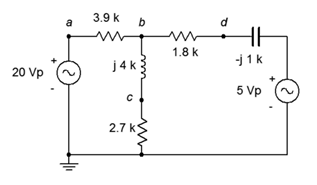
Figura\(\PageIndex{11}\)
21. Dado el circuito en la Figura\(\PageIndex{12}\), utilizar el análisis nodal para determinar\(v_{ba}\). \(E_1 = 1\angle 0^{\circ}\),\(E_2 = 2\angle 0^{\circ}\).
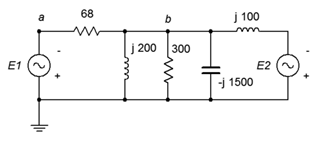
Figura\(\PageIndex{12}\)
22. Dado el circuito en la Figura\(\PageIndex{13}\), utilizar el análisis nodal para determinar\(v_{ad}\). \(E_1 = 9\angle 0^{\circ}\),\(E_2 = 5\angle 40^{\circ}\).
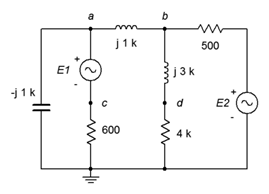
Figura\(\PageIndex{13}\)
23. Utilice el análisis nodal para encontrar\(v_{cb}\) en el circuito de la Figura\(\PageIndex{14}\). \(E_1 = 10\angle −180^{\circ}\),\(E_2 = 25\angle 0^{\circ}\).
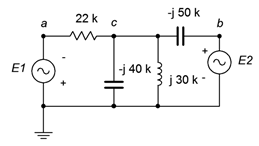
Figura\(\PageIndex{14}\)
24. Dado el circuito en la Figura\(\PageIndex{15}\), utilizar el análisis nodal para determinar\(v_{bc}\). \(E = 20\angle 0^{\circ}\),\(R_1\) = 10 k\(\Omega\),\(R_2\) = 30 k\(\Omega\),\(R_3\) = 1 k\(\Omega\),\(X_C = −j15\) k\(\Omega\),\(X_L = j20\) k\(\Omega\).
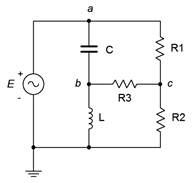
Figura\(\PageIndex{15}\)
25. Dado el circuito de la Figura\(\PageIndex{16}\), escribir las ecuaciones de bucle de malla y determinar\(v_b\).
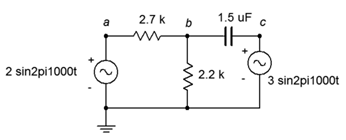
Figura\(\PageIndex{16}\)
26. Utilice el análisis de malla para encontrar la corriente a través de la\(\Omega\) resistencia de 2.7 k en el circuito de la Figura\(\PageIndex{16}\).
27. Utilice el análisis de malla para encontrar la corriente a través de la\(\Omega\) resistencia 75 en el circuito de la Figura\(\PageIndex{10}\).
28. Dado el circuito de la Figura\(\PageIndex{10}\), escribir las ecuaciones de bucle de malla y determinar\(v_c\).
29. Dado el circuito de la Figura\(\PageIndex{11}\), escribir las ecuaciones de bucle de malla y determinar\(v_b\).
30. Utilice el análisis de malla para encontrar la corriente a través de la\(\Omega\) resistencia de 1.8 k en el circuito de la Figura\(\PageIndex{11}\).
31. Utilice el análisis de malla para encontrar la corriente a través del\(j200 \Omega\) inductor en la Figura\(\PageIndex{12}\). \(E_1 = 1\angle 0^{\circ}\),\(E_2 = 2\angle 0^{\circ}\).
32. Dado el circuito de la Figura\(\PageIndex{12}\), escribir las ecuaciones de bucle de malla y determinar\(v_b\). Considera usar primero la simplificación paralela. \(E_1 = 36\angle −90^{\circ}\),\(E_2 = 24\angle −90^{\circ}\).
33. Dado el circuito de la Figura\(\PageIndex{13}\), utilice el análisis de malla para determinar\(v_{cd}\). \(E_1 = 0.1\angle 0^{\circ}\),\(E_2 = 0.5\angle 0^{\circ}\).
34. Utilice el análisis de malla para encontrar la corriente a través de la\(\Omega\) resistencia 600 en el circuito de la Figura\(\PageIndex{13}\). \(E_1 = 9\angle 0^{\circ}\),\(E_2 = 5\angle 40^{\circ}\).
35. Utilice el análisis de malla para encontrar la corriente a través del\(−j200 \Omega\) condensador en el circuito de la Figura\(\PageIndex{17}\). \(E_1 = 18\angle 0^{\circ}\),\(E_2 = 12\angle 90^{\circ}\).
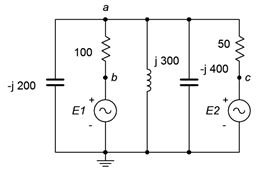
Figura\(\PageIndex{17}\)
36. Dado el circuito de la Figura\(\PageIndex{17}\), utilice el análisis de malla para determinar\(v_{ac}\). \(E_1 = 1\angle 0^{\circ}\),\(E_2 = 500E−3\angle 0^{\circ}\).
37. Dado el circuito de la Figura\(\PageIndex{14}\), utilice el análisis de malla para determinar\(v_c\). \(E_1 = 10\angle −180^{\circ}\),\(E_2 = 25\angle 0^{\circ}\).
38. Utilice el análisis de malla para encontrar la corriente a través de la\(\Omega\) resistencia de 22 k en el circuito de la Figura\(\PageIndex{14}\). \(E_1 = 24\angle 0^{\circ}\),\(E_2 = 36\angle 0^{\circ}\).
39. Utilice el análisis de malla para encontrar la corriente a través del\(j300 \Omega\) inductor en la Figura\(\PageIndex{18}\). \(E_1 = 1\angle 0^{\circ}\),\(E_2 = 10\angle 90^{\circ}\).
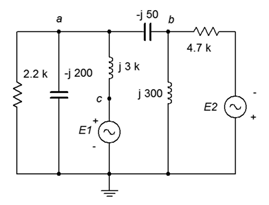
Figura\(\PageIndex{18}\)
40. Dado el circuito de la Figura\(\PageIndex{18}\), utilice el análisis de malla para determinar\(v_a\). \(E_1 = 100\angle 0^{\circ}\),\(E_2 = 90\angle 0^{\circ}\).
41. Dado el circuito de la Figura\(\PageIndex{15}\), utilice el análisis de malla para determinar\(v_{bc}\). \(E = 10\angle 0^{\circ}\),\(R_1\) = 1 k\(\Omega\),\(R_2\) = 2 k\(\Omega\),\(R_3\) = 3 k\(\Omega\),\(X_C = −j4\) k\(\Omega\),\(X_L = j8\) k\(\Omega\).
42. Utilice el análisis de malla para encontrar la corriente a través de la resistencia\(R_3\) en el circuito de la Figura\(\PageIndex{15}\). \(E = 20\angle 0^{\circ}\),\(R_1\) = 10 k\(\Omega\),\(R_2\) = 30 k\(\Omega\),\(R_3\) = 1 k\(\Omega\),\(X_C = −j15\) k\(\Omega\),\(X_L = j20\) k\(\Omega\).
43. Utilice el análisis de malla para encontrar la corriente a través de la resistencia\(R_3\) en la Figura\(\PageIndex{19}\). \(E = 60\angle 0^{\circ}\),\(R_1\) = 1 k\(\Omega\),\(R_2\) = 2 k\(\Omega\),\(R_3\) = 3 k\(\Omega\),\(X_C = −j10\) k\(\Omega\),\(X_L = j20\) k\(\Omega\).
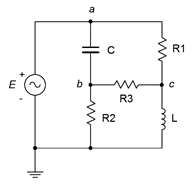
Figura\(\PageIndex{19}\)
44. Dado el circuito de la Figura\(\PageIndex{19}\), utilice el análisis de malla para determinar\(v_{bc}\). \(E = 120\angle 90^{\circ}\),\(R_1\) = 100 k\(\Omega\),\(R_2\) = 20 k\(\Omega\),\(R_3\) = 10 k\(\Omega\),\(X_C = −j5\) k\(\Omega\),\(X_L = j20\) k\(\Omega\).
45. Dado el circuito de la Figura\(\PageIndex{20}\), utilice el análisis de malla para determinar\(v_b\). Considere usar la conversión de origen. \(E = 12\angle 0^{\circ}\),\(I = 10E−3\angle 0^{\circ}\).
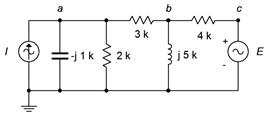
Figura\(\PageIndex{20}\)
46. Utilice el análisis de malla para encontrar la corriente a través de la\(\Omega\) resistencia 3 en el circuito de la Figura\(\PageIndex{20}\). Considere usar la conversión de origen. \(E = 15\angle 90^{\circ}\),\(I = 10E−3\angle 0^{\circ}\).
47. Utilice el análisis de malla para encontrar la corriente a través de la\(\Omega\) resistencia de 2.2 k en el circuito de la Figura\(\PageIndex{21}\). \(E = 3.3\angle 0^{\circ}\),\(I = 2.1E−3\angle 0^{\circ}\).
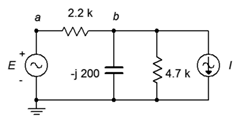
Figura\(\PageIndex{21}\)
48. Dado el circuito de la Figura\(\PageIndex{21}\), utilice el análisis de malla para determinar\(v_b\). \(E = 10\angle 0^{\circ}\),\(I = 30E−3\angle 90^{\circ}\).
49. Dado el circuito en la Figura\(\PageIndex{22}\), utilizar el análisis nodal para determinar\(v_{ab}\).
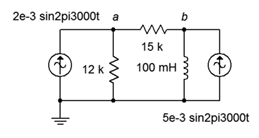
Figura\(\PageIndex{22}\)
50. Utilice el análisis nodal para encontrar la corriente a través del inductor de 100 mH en el circuito de la Figura\(\PageIndex{22}\).
51. Utilice el análisis nodal para encontrar la corriente a través de la\(\Omega\) resistencia 330 en el circuito de la Figura\(\PageIndex{23}\).
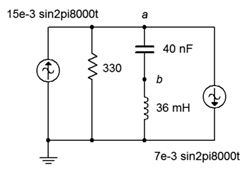
Figura\(\PageIndex{23}\)
52. Dado el circuito de la Figura\(\PageIndex{23}\), escribir las ecuaciones de nodo y determinar\(v_b\).
53. Dado el circuito en la Figura\(\PageIndex{19}\), utilizar el análisis nodal para determinar\(v_{bc}\). \(E = 120\angle 0^{\circ}\),\(R_1\) = 1 k\(\Omega\),\(R_2\) = 2 k\(\Omega\),\(R_3\) = 3 k\(\Omega\),\(X_C = −j10\) k\(\Omega\),\(X_L = j20\) k\(\Omega\).
54. Determinar la corriente a través de la\(\Omega\) resistencia de 10 k en el circuito de la Figura\(\PageIndex{24}\) si\(I_1 = 10E−3\angle −90^{\circ}\).
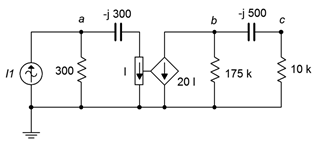
Figura\(\PageIndex{24}\)
55. Determinar\(v_b\) en el circuito de la Figura\(\PageIndex{24}\) si la fuente\(I_1 = 20E−3\angle 0^{\circ}\).
56. Determinar\(v_c\) en el circuito de la Figura\(\PageIndex{25}\) si la fuente\(E = 3\angle 120^{\circ}\).
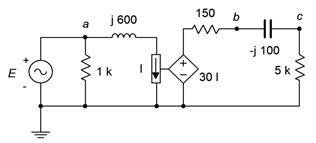
Figura\(\PageIndex{25}\)
57. Determinar la corriente a través de la\(\Omega\) resistencia de 5 k en el circuito de la Figura\(\PageIndex{25}\) si\(E = 10\angle 0^{\circ}\).
58. En el circuito de la Figura\(\PageIndex{26}\), determine la corriente del condensador si la fuente\(E = 12\angle 0^{\circ}\).
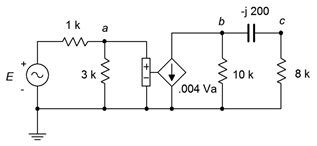
Figura\(\PageIndex{26}\)
59. En el circuito de la Figura\(\PageIndex{26}\), determinar\(v_c\) si la fuente\(E = 8\angle 90^{\circ}\).
60. En el circuito de la Figura\(\PageIndex{27}\), determinar\(v_b\) si la fuente\(E = 12\angle −90^{\circ}\).
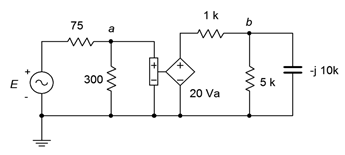
Figura\(\PageIndex{27}\)
61. En el circuito de la Figura\(\PageIndex{27}\), determinar la corriente que fluye hacia la\(\Omega\) resistencia de 1 k si la fuente\(E = 6\angle 0^{\circ}\).
62. En el circuito de la Figura\(\PageIndex{28}\), determine la corriente que fluye hacia la\(\Omega\) resistencia 600 si\(I_1 = 1E−3\angle 180^{\circ}\).
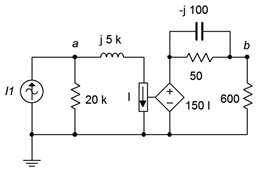
Figura\(\PageIndex{28}\)
63. Determinar\(v_a\) y\(v_b\) en el circuito de la Figura\(\PageIndex{28}\) si la fuente\(I_1 = 2E−3\angle 0^{\circ}\).
64. Determinar\(v_a\) en el circuito de la Figura\(\PageIndex{29}\) si la fuente\(E = 2\angle 0^{\circ}\).
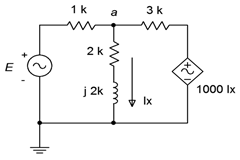
Figura\(\PageIndex{29}\)
65. Dado el circuito de la Figura\(\PageIndex{29}\), determinar la corriente que fluye a través de la\(\Omega\) resistencia de 1 k. Supongamos que\(E = 15\angle 45^{\circ}\).
66. Dado el circuito de la Figura\(\PageIndex{30}\), determinar la corriente que fluye a través de la\(\Omega\) resistencia de 3 k si la fuente\(E = 25\angle 33^{\circ}\).
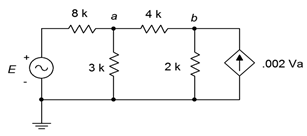
Figura\(\PageIndex{30}\)
67. Dado el circuito de la Figura\(\PageIndex{30}\), determinar\(v_{ab}\). Asumir la fuente\(E = 15\angle −112^{\circ}\).
68. En el circuito de la Figura\(\PageIndex{31}\), determinar\(v_d\).
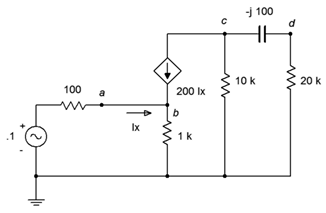
Figura\(\PageIndex{31}\)
69. Dado el circuito de la Figura\(\PageIndex{31}\), determinar la corriente que fluye a través de la\(\Omega\) resistencia de 1 k.
70. Dado el circuito de la Figura\(\PageIndex{32}\), determinar la corriente que fluye a través de la\(\Omega\) resistencia 100.
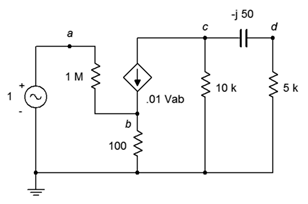
Figura\(\PageIndex{32}\)
71. Determinar\(v_d\) en el circuito de la Figura\(\PageIndex{32}\).
72. Determinar\(v_{ab}\) en el circuito de la Figura\(\PageIndex{33}\). \(E = 10\angle 0^{\circ}\)
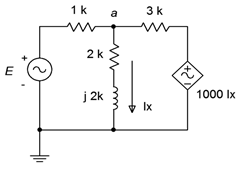
Figura\(\PageIndex{33}\)
Desafío
73. Dado el circuito de la Figura\(\PageIndex{34}\), escribir las ecuaciones de nodo. \(E_1 = 50\angle 0^{\circ}\),\(E_2 = 35\angle 120^{\circ}\),\(I = 500E−3\angle 90^{\circ}\).
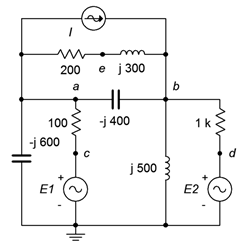
Figura\(\PageIndex{34}\)
74. Dado el circuito de la Figura\(\PageIndex{34}\), use análisis de malla o nodal para determinar\(v_{ed}\). \(E_1 = 9\angle 0^{\circ}\),\(E_2 = 12\angle 0^{\circ}\),\(I = 50E−3\angle 0^{\circ}\).
75. Dado el circuito de la Figura\(\PageIndex{35}\), utilice el análisis de malla para determinar\(v_{fc}\). \(E_1 = 12\angle 0^{\circ}\),\(E_2 = 48\angle 0^{\circ}\),\(E_3 = 36\angle 70^{\circ}\).
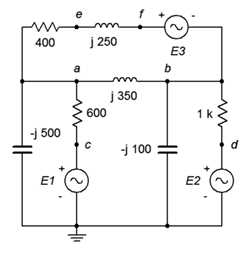
Figura\(\PageIndex{35}\)
76. Encuentre voltaje\(v_{bc}\) en el circuito de la Figura\(\PageIndex{36}\) usando análisis de malla o nodal. \(E = 100\angle 0^{\circ}\),\(R_1 = R_2 = 2\) k\(\Omega\),\(R_3\) = 3 k\(\Omega\),\(R_4\) = 10 k\(\Omega\),\(R_5\) = 5 k\(\Omega\),\(X_{C1} = X_{C2} = −j2\) k\(\Omega\).
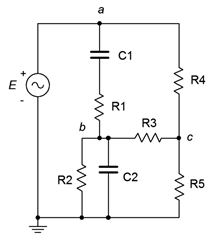
Figura\(\PageIndex{36}\)
77. Dado el circuito en la Figura\(\PageIndex{37}\), utilice el análisis nodal para encontrar\(v_{ac}\). \(I_1 = 8E−3\angle 0^{\circ}\),\(I_2 = 12E−3\angle 0^{\circ}\),\(E = 50\angle 0^{\circ}\).
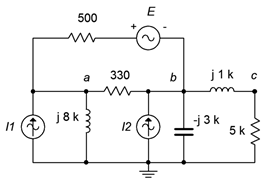
Figura\(\PageIndex{37}\)
78. Dado el circuito en la Figura\(\PageIndex{38}\), utilizar el análisis nodal para determinar\(v_{ad}\). \(I_1 = 0.1\angle 0^{\circ}\),\(I_2 = 0.2\angle 0^{\circ}\),\(I_3 = 0.3\angle 0^{\circ}\).
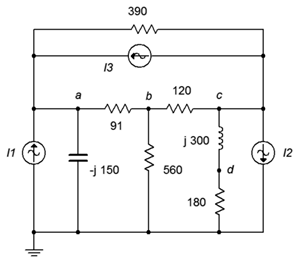
Figura\(\PageIndex{38}\)
79. Dado el circuito de la Figura\(\PageIndex{39}\), determinar\(v_{ad}\). \(E_1 = 15\angle 0^{\circ}\),\(E_2 = 6\angle 0^{\circ}\),\(I = 100E−3\angle 0^{\circ}\).
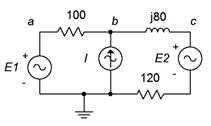
Figura\(\PageIndex{39}\)
80. Dado el circuito de la Figura\(\PageIndex{40}\), determinar\(v_{ad}\). \(E_1 = 22\angle 0^{\circ}\),\(E_2 = −10\angle 0^{\circ}\),\(I = 2E−3\angle 0^{\circ}\).
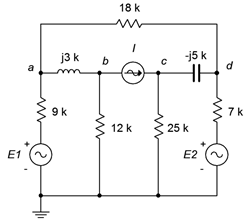
Figura\(\PageIndex{40}\)
81. Dado el circuito de la Figura\(\PageIndex{41}\), determinar\(v_{ab}\). \(I_1 = 1.2\angle 0^{\circ}\),\(I_2 = 2\angle 120^{\circ}\),\(E = 75\angle 0^{\circ}\).
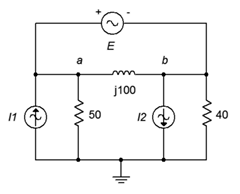
Figura\(\PageIndex{41}\)
82. Dado el circuito de la Figura\(\PageIndex{42}\), determinar\(v_{ad}\). \(I_1 = 0.8\angle 0^{\circ}\),\(I_2 = 0.2\angle 180^{\circ}\),\(I_3 = 0.1\angle 0^{\circ}\),\(E = 15\angle 0^{\circ}\).
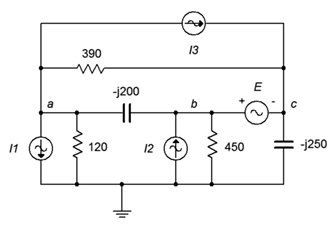
Figura\(\PageIndex{42}\)
Simulación
83. Realizar una simulación de análisis transitorio en el circuito del problema 25 (Figura\(\PageIndex{16}\)) para verificar los resultados para\(v_b\).
84. Investigar la variación de\(v_b\) debido a la frecuencia en el problema 25 (Figura\(\PageIndex{16}\)) mediante la realización de una simulación AC. Ejecute la simulación desde 10 Hz hasta 100 kHz.
85. Investigar la variación de la tolerancia\(v_b\) debida a componentes en el problema 25 (Figura\(\PageIndex{16}\)) mediante la realización de una simulación de Monte Carlo. Aplique una tolerancia del 10% a las resistencias y al condensador.
86. Realizar una simulación de análisis transitorio en el circuito del problema 28 (Figura\(\PageIndex{10}\)) para verificar los resultados para\(v_c\).
87. Investigar la variación de\(v_b\) debido a la frecuencia en el problema 28 (Figura\(\PageIndex{10}\)) mediante la realización de una simulación AC. Ejecute la simulación desde 1 Hz hasta 10 kHz.
88. Investigar la variación de la tolerancia\(v_b\) debida a componentes en el problema 28 (Figura\(\PageIndex{10}\)) mediante la realización de una simulación de Monte Carlo. Aplicar una tolerancia del 10% a las resistencias y capacitores.


