2.2: El cruce PN
- Page ID
- 83392
Si tuviéramos que crear una región de material N colindando con una región de material P en un solo cristal, se produce una situación interesante. Suponiendo que el cristal no está en cero absoluto, la energía térmica en el sistema hará que algunos de los electrones libres en el material N “caigan” en los agujeros sobrantes del material P contiguo. Esto creará una región que está desprovista de portadores de carga (recuerde, los electrones son el portador de carga mayoritario en el material N mientras que los agujeros son el portador de carga mayoritario en el material P). Es decir, el área donde los materiales N y P hacen tope está agotada de electrones y huecos disponibles, y por lo tanto nos referimos a ella como una región de agotamiento. Esto se representa en la Figura\(\PageIndex{1}\). El exceso de electrones del material N se denota con signos menos mientras que los agujeros sobrantes del material P se denotan con signos más. En la interfaz, los electrones libres se han recombinado con agujeros. Cuando un electrón se recombina, deja atrás un ion positivo en el material N (mostrado aquí como un signo más en un círculo) y produce un ion negativo en el material P (mostrado como un signo menos en un círculo).
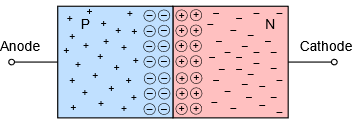
Figura\(\PageIndex{1}\): Unión PN.
Ahora tenemos una región agotada de portadores de carga y esto tendrá un efecto en la capacidad de establecer un flujo de corriente a través del dispositivo. Tenemos, en esencia, creado un cerro de energía que habrá que superar.
Para entender el concepto del cerro energético, recordemos que en el capítulo anterior se descubrió que el dopaje de un cristal intrínseco desplazaría el nivel Fermi. Para el material N, el nivel de Fermi se desplaza hacia arriba, hacia la banda de conducción. En contraste, para el material P el nivel de Fermi se desplaza hacia abajo, más cerca de la banda de valencia. Cuando colindan dos regiones disímiles, como en el caso aquí, las bandas de energía se ajustarán para que los niveles de Fermi sean consistentes. Efectivamente, esto hace que las bandas del material P suban con respecto a las bandas del material N. La interfaz entre ambos aparece como un cerro, y esta es la región de agotamiento antes mencionada. Esta situación se representa gráficamente en la Figura\(\PageIndex{2}\). Compare este diagrama de energía con los diagramas de energía para material N y material P presentados en el capítulo anterior. Simplemente alineando los niveles de Fermi, debería quedar claro cómo llegamos al nuevo diagrama de energía.
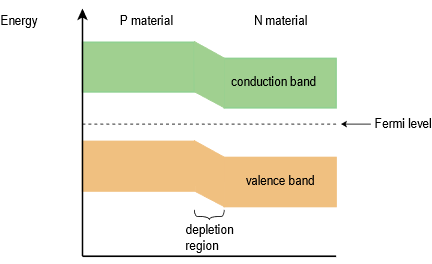
Figura\(\PageIndex{2}\): Bandas de energía en unión PN.
Ahora consideremos qué pasa si conectáramos este dispositivo a una fuente de voltaje externa como se muestra en la Figura\(\PageIndex{3}\). Obviamente, hay dos formas de orientar la unión PN con respecto a la fuente de voltaje. Esta versión se conoce como sesgo hacia adelante.
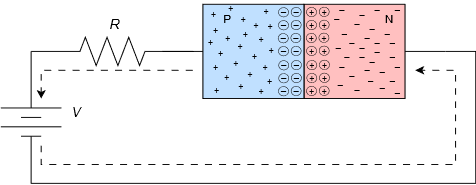
Figura\(\PageIndex{3}\): Empalme PN conectado a fuente de voltaje externa.
2.2.1: Sesgo hacia delante
La línea punteada de la Figura\(\PageIndex{3}\) muestra la dirección del flujo de electrones (opuesta a la dirección del flujo convencional). Primero, los electrones fluyen desde el terminal negativo de la batería hacia el material N. En el material N, los portadores mayoritarios son electrones y es fácil que estos electrones se muevan a través del material N. Al ingresar a la región de agotamiento, si el potencial suministrado es lo suficientemente alto, los electrones pueden difunderse hacia el material P donde hay una gran cantidad de agujeros de menor energía. A partir de aquí, los electrones pueden migrar a través del terminal positivo de la fuente, completando el circuito (se ha agregado la resistencia para limitar el flujo máximo de corriente). El “truco” aquí es asegurar que el potencial suministrado es lo suficientemente grande como para superar el efecto de la región de agotamiento. Es decir, un cierto voltaje caerá a través de la región de agotamiento para lograr el flujo de corriente. Este potencial requerido se denomina potencial de barrera o caída de voltaje directo. El valor preciso depende del material utilizado. Para los dispositivos de silicio, el potencial de barrera generalmente se estima en alrededor de 0.7 voltios. Para los dispositivos de germanio está más cerca de 0.3 voltios, mientras que los LEDs pueden exhibir potenciales de barrera en las proximidades de 1.5 a 3 voltios, en parte dependiendo del color.
Otra forma de pensar al respecto es que la adición de la fuente de voltaje “aplana” la colina de energía inherente de la unión. Una vez que el voltaje de polarización directa aplicado es al menos tan grande como la colina, la corriente puede fluir fácilmente.
2.2.2: Sesgo inverso
Si la polaridad de la fuente de voltaje se invierte en la Figura\(\PageIndex{3}\), el comportamiento de la unión PN se altera radicalmente. En este caso, los electrones en el material N serán atraídos hacia el terminal positivo de la fuente mientras que los agujeros del material P serán dibujados hacia el terminal negativo, creando una corriente pequeña y de corta duración. Esto tiene el efecto de ensanchar la región de agotamiento y una vez que alcanza el potencial suministrado, cesa el flujo de corriente. En esencia, hemos aumentado el tamaño del cerro energético. Incrementos adicionales en la tensión de la fuente sólo sirven para empeorar la situación. La región de agotamiento simplemente se expande para llenar el vacío, por así decirlo. Idealmente, la unión PN actúa como un circuito abierto con un voltaje de polarización inversa aplicado.
Esta asimetría en respuesta a un potencial suministrado resulta extraordinariamente útil. Quizás el más simple de todos los dispositivos semiconductores es el diodo. En su forma básica un diodo es solo una unión PN. Es un dispositivo que permitirá que la corriente pase fácilmente en una dirección pero evitará el flujo de corriente en la dirección opuesta.
2.2.3: Ecuación de Shockley
Podemos cuantificar el comportamiento de la unión PN mediante el uso de una ecuación derivada de William Shockley.
\[I = I_S \left( e^{\frac{V_D q}{n k T}} −1 \right) \label{2.1} \]
Dónde
\(I\)es la corriente del diodo,
\(I_S\)es la corriente de saturación inversa,
\(V_D\)es el voltaje a través del diodo,
\(q\)es la carga de un electrón, 1.6E−19 culombios,
\(n\)es el factor de calidad (típicamente entre 1 y 2),
\(k\)es la constante de Boltzmann, 1.38E−23 Julios/Kelvin,
\(T\)es la temperatura en kelvin.
A 300 Kelvin,\(q/kT\) es aproximadamente 38.6. En consecuencia, incluso para voltajes directos (positivos) muy pequeños, se puede ignorar el término “−1". Además, no\(I_S\) es una constante. Aumenta con la temperatura, duplicándose aproximadamente por cada subida de 10 C° (más sobre esto en un momento).
Si trazamos la ecuación de Shockley usando valores típicos para un dispositivo de silicio, llegamos a la curva que se muestra en la Figura\(\PageIndex{4}\). Esto representa la corriente de unión como una función de la tensión directa (positiva) del dispositivo. Se trata únicamente de una curva representativa. Si bien todos los diodos de silicio exhibirán esta misma forma general, el valor preciso de la corriente para un voltaje específico variará dependiendo del diseño del dispositivo.
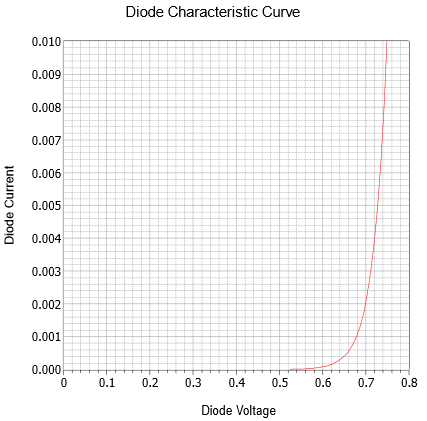
Figura\(\PageIndex{4}\): Curva característica de la unión PN de silicio con polarización directa.
Para potenciales por debajo de aproximadamente 0.5 voltios, la corriente es prácticamente inexistente. Por encima de este valor, la corriente se eleva rápidamente, volviéndose casi vertical después de aproximadamente 0.7 voltios. Si la gráfica se recreara usando una temperatura más alta, el efecto sería desplazar la curva hacia la izquierda (es decir, una corriente más alta para un voltaje dado).
Si tuviéramos que alterar la gráfica para usar una escala de corriente logarítmica en lugar de una escala lineal, la gráfica de la Figura\(\PageIndex{5}\) resulta. La gráfica de línea recta resultante muestra claramente la relación logarítmica entre el voltaje y la corriente del diodo.
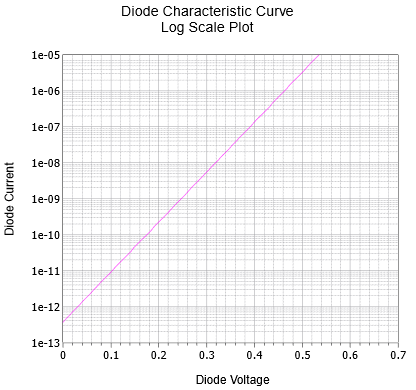
Figura\(\PageIndex{5}\): Curva característica de unión PN de silicio con polarización directa usando escala logarítmica.
Para voltajes negativos (polarización inversa), la ecuación de Shockley predice una corriente de diodo insignificante. Esto es cierto hasta cierto punto. La ecuación no modela los efectos del desglose. Cuando el voltaje inverso es lo suficientemente grande, el diodo comenzará a conducir. Esto se muestra en la Figura\(\PageIndex{6}\). En el primer cuadrante vemos la misma forma general que encontramos en la Figura\(\PageIndex{4}\). \(V_F\)es el voltaje de “rodilla” hacia adelante (aproximadamente 0.7 voltios para silicio). \(I_R\)es la corriente de saturación inversa (idealmente cero pero en realidad fluirá una cantidad muy pequeña de corriente). \(V_R\)es el voltaje de ruptura inverso. Tenga en cuenta que la corriente aumenta rápidamente una vez que se alcanza este voltaje inverso.
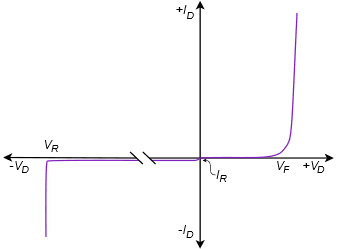
Figura\(\PageIndex{6}\): Curva I-V directa e inversa simplificada para diodo.
En general, los diodos no deben operarse en la región de ruptura (la excepción son los diodos Zener). Hay dos mecanismos detrás de este fenómeno. El efecto Zener, llamado así por Clarence Zener, predomina cuando los niveles de dopaje son altos y produce voltajes de ruptura por debajo de aproximadamente cinco o seis voltios. Se debe a la producción de un campo eléctrico muy alto a través de la región de agotamiento que luego resulta en la producción de una alta corriente a través de túneles de electrones. En los dispositivos que utilizan niveles más bajos de dopaje, domina la avalancha. En esta instancia, un alto campo eléctrico acelera los electrones libres hasta el punto en que pueden impactar los átomos circundantes y crear nuevos pares electrón-agujero, creando así nuevos electrones libres que pueden repetir el proceso, resultando en un rápido aumento de la corriente.
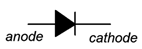
Figura\(\PageIndex{7}\): Símbolo esquemático de diodo (ANSI).
Figura\(\PageIndex{8}\): Símbolo esquemático de diodo alternativo (IEC).
El símbolo esquemático para un diodo básico de conmutación o rectificación se muestra en la Figura\(\PageIndex{7}\). Este es el estándar ANSI que predomina en América del Norte. El material P es el ánodo mientras que el material N es el cátodo 1. Como regla general para los símbolos esquemáticos de semiconductores, las flechas apuntan hacia N material. En este caso, la flecha también apunta en la dirección del flujo de corriente convencional fácil. La figura\(\PageIndex{8}\) muestra un símbolo esquemático alternativo, la norma internacional IEC, siendo la diferencia que se encuentra en forma de esquema sin rellenar el cuerpo.

Figura\(\PageIndex{9}\): Caso DO-204.

Figura\(\PageIndex{10}\): Caso DO-4. Cortesía de Vishay Intertechnology, Inc.
Cuando se trata del empaque de dispositivos físicos, los dispositivos de corriente y potencia pequeños y medianos para montaje en orificios pasantes incluyen el DO-35 y el DO-204, con el número de modelo estampado en el cuerpo. El tamaño típico es comparable a una resistencia de 1/4 a 1/8 vatios. Como se ve en\(\PageIndex{9}\) la Figura el extremo del cátodo se denota por una banda, que recuerda a la barra en el símbolo esquemático. También hay disponibles paquetes de montaje en superficie. Los dispositivos que manejan corrientes y potencias más altas a menudo vienen en estilos de perno o perno, como el DO-4 que se muestra en la Figura\(\PageIndex{10}\). Estos paquetes facilitan el montaje en una placa metálica o disipador de calor para ayudar a disipar el exceso de calor.
Referencias
1 El cátodo a menudo se denota por a\(k\). Esto probablemente se deba a la raíz griega de la palabra, kathodos.


