4.9: Ejercicios
- Page ID
- 83446
4.9.1: Problemas de análisis
1. Determinar\(\beta\) si\(\alpha\) = 0.99.
2. Determinar\(\alpha\) si\(\beta\) = 200.
3. Determinar las corrientes para el circuito de la Figura\(\PageIndex{1}\) si\(V_{BB} = 5\) V,\(V_{CC} = 20\) V,\(R_B = 200\) k\(\Omega\),\(R_C = 2\) k\(\Omega\),\(\beta\) = 100.
4. Determinar las tensiones del transistor para el circuito de la Figura\(\PageIndex{1}\) si\(V_{BB} = 5\) V,\(V_{CC} = 20\) V,\(R_B = 200\) k\(\Omega\),\(R_C = 2\) k\(\Omega\),\(\beta\) = 200.
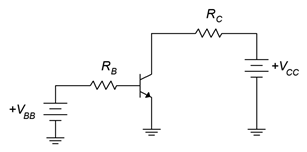
Figura\(\PageIndex{1}\)
5. Determine la corriente LED en el circuito de la Figura\(\PageIndex{2}\) si\(V_{logic} = 5\) V,\(V_{CC} = 5\) V,\(V_{LED} = 2.1\) V,\(R_B = 3.6\) k\(\Omega\),\(R_C = 270\)\(\Omega\),\(\beta\) = 100.
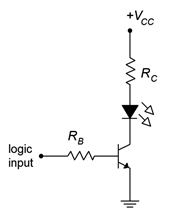
Figura\(\PageIndex{2}\)
6. Determine la corriente LED en el circuito de la Figura\(\PageIndex{2}\) si\(V_{logic} = 0\) V,\(V_{CC} = 5\) V,\(V_{LED} = 2.1\) V,\(R_B = 3.6\) k\(\Omega\),\(R_C = 270\)\(\Omega\),\(\beta\) = 100.
7. Determine la corriente LED en el circuito de la Figura\(\PageIndex{3}\) si\(V_{logic} = 5\) V,\(V_{EE} = 5\) V,\(V_{LED} = 2.2\) V,\(R_B = 2.7\) k\(\Omega\),\(R_C = 220\)\(\Omega\),\(\beta\) = 100.
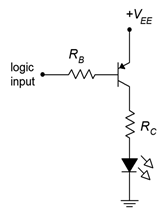
Figura\(\PageIndex{3}\)
8. Determine la corriente LED en el circuito de la Figura\(\PageIndex{3}\) si\(V_{logic} = 0\) V,\(V_{EE} = 5\) V,\(V_{LED} = 2.2\) V,\(R_B = 2.7\) k\(\Omega\),\(R_C = 220\)\(\Omega\),\(\beta\) = 100.
9. Determine la corriente LED en el circuito de la Figura\(\PageIndex{4}\) si\(V_{logic} = 3.6\) V,\(V_{CC} = 10\) V,\(V_{LED} = 2.3\) V,\(R_E = 270\)\(\Omega\),\(\beta\) = 200.
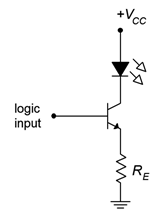
Figura\(\PageIndex{4}\)
10. Determinar la corriente LED en el circuito de la Figura\(\PageIndex{4}\). \(V_{logic} = 0\)V,\(V_{CC} = 10\) V,\(V_{LED} = 2.3\) V,\(R_E = 270\)\(\Omega\),\(\beta\) = 200.
11. Usando la hoja de datos 2N3904, determine\(V_{CE(sat)}\) si\(I_C = 30\) mA y\(I_B = 1\) mA.
12. Usando la hoja de datos 2N3904, determine el cambio porcentual en\(\beta\) si\(I_C = 10\) mA y la temperatura aumenta de 25\(^{\circ}\) C a 125\(^{\circ}\) C.
13. Usando la hoja de datos 2N3904, determine el cambio porcentual en\(\beta\) si\(I_C = 40\) mA y la temperatura desciende de 25\(^{\circ}\) C a −55\(^{\circ}\) C.
4.9.2: Problemas de diseño
14. Usando la Figura\(\PageIndex{1}\), determine un valor\(R_B\)\(I_C\) para establecer en 5 mA si\(V_{BB} = 5\) V,\(V_{CC} = 25\) V,\(R_C = 2\) k\(\Omega\),\(\beta\) = 100.
15. Usando la Figura\(\PageIndex{1}\), determine un valor\(R_C\)\(V_{CE}\) para establecer en 6 V si\(V_{BB} = 10\) V,\(V_{CC} = 25\) V,\(R_B = 330\) k\(\Omega\),\(\beta\) = 200.
16. Para el circuito de la Figura\(\PageIndex{2}\), determine un valor\(R_C\) para establecer la corriente del LED en 15 mA. \(V_{logic} = 5\)V,\(V_{CC} = 5\) V,\(V_{LED} = 1.6\) V,\(R_B = 3.3\) k\(\Omega\).
17. Para el circuito de la Figura\(\PageIndex{3}\), determine un valor\(R_C\) para establecer la corriente del LED en 20 mA. \(V_{logic} = 0\)V,\(V_{EE} = 5\) V,\(V_{LED} = 2.0\) V,\(R_B = 2.7\) k\(\Omega\).
18. Para el circuito de la Figura\(\PageIndex{4}\), determine un valor\(R_E\) para establecer la corriente del LED en 25 mA. \(V_{logic} = 5\)V,\(V_{CC} = 9\) V,\(V_{LED} = 2.8\) V.
4.9.3: Problemas de desafío
19. Determinar los valores máximo y mínimo para\(I_C\) en el circuito de la Figura\(\PageIndex{1}\) si todas las resistencias tienen una tolerancia del 10% y\(\beta\) = rangos de 100 a 200. \(V_{BB} = 5\)V,\(V_{CC} = 20\) V,\(R_B = 200\) k\(\Omega\),\(R_C = 2\) k\(\Omega\).
20. Derive y dibuja un circuito conductor de LED no saturante PNP.
4.9.4: Problemas de simulación por computadora
21. Simular el circuito del Problema 3.
22. Simular el circuito del Problema 5.
23. Simular el circuito del Problema 7.
24. Verificar el diseño del Problema 14 usando un simulador.


