8.3: Líneas de Operación y Carga Clase A
- Page ID
- 83421
La corriente de señal en el amplificador de clase A fluye continuamente a lo largo de todo el ciclo de la forma de onda. En última instancia, nos gustaría saber cuán grande puede ser esta señal antes de que sea limitada y groseramente distorsionada. Para ello, necesitamos examinar el equivalente de CA del amplificador. En la Figura se muestra un equivalente genérico de CA\(\PageIndex{1}\). Esto incluye resistencias tanto de colector de CA como de emisor, por lo que se puede usar para amplificadores de emisor comunes inundados o no inundados o para seguidores de emisores. Si no se usa una de las resistencias (por ejemplo,\(r_C\) en un seguidor), podemos simplemente sustituirla por un valor de cero.
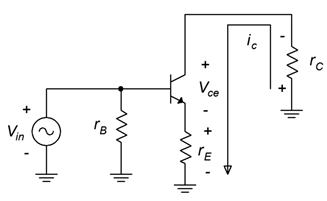
Figura\(\PageIndex{1}\): Circuito equivalente de CA.
Las polaridades de voltaje y la dirección de la corriente se muestran para un voltaje de entrada positivo. Para determinar la oscilación de voltaje de carga máxima (cumplimiento), necesitaremos construir una línea de carga de CA como se muestra en la Figura\(\PageIndex{2}\).
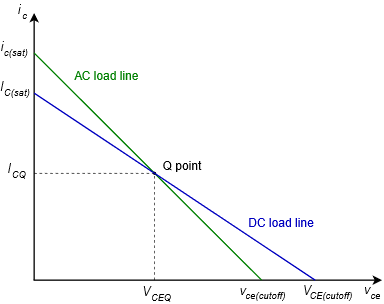
Figura\(\PageIndex{2}\): Líneas de carga de CA y CC.
La línea de carga de CA es similar a la línea de carga de CC que se utilizó para analizar circuitos de polarización. Al igual que en la versión de CC, habrá un voltaje de corte,\(v_{CE(cutoff)}\), y una corriente de saturación,\(i_{C(sat)}\). Las líneas de carga de CA y CC normalmente no son las mismas, sin embargo, deben compartir un punto en común, y ese es el punto Q. Por lo general, la pendiente de la línea de carga de CA es más pronunciada que la de la línea de carga de CC. Esto se debe a que la resistencia de CA tiende a ser menor que la resistencia de CC debido a la carga y la derivación del condensador. En consecuencia,\(v_{CE(cutoff)}\) tiende a ser más pequeño que\(V_{CE(cutoff)}\) y\(i_{C(sat)}\) tiende a ser más grande que\(I_{C(sat)}\).
Para determinar expresiones para los puntos finales de la línea de carga de CA, examinemos el circuito equivalente de CA. Debido a que ambas líneas de carga comparten el punto Q, podemos considerar que el circuito de la Figura\(\PageIndex{1}\) tiene una corriente sin señal de\(I_{CQ}\) y una tensión de transistor sin señal de\(V_{CEQ}\). A medida que la señal de entrada crece,\(i_C\) aumenta. El efecto de esto es aumentar las caídas de voltaje a través\(r_E\) y\(r_C\) debido a la ley de Ohm. Esto, a su vez, obliga\(v_{CE}\) a disminuir debido a KVL. La corriente del colector solo puede aumentar hasta el punto donde\(v_{CE}\) cae a 0 V. Esto es un aumento máximo de\(V_{CEQ}/(r_C+r_E)\). Por lo tanto
\[i_{C(sat )} = I_{CQ} + \frac{V_{CEQ}}{r_E+r_C} \label{8.1} \]
En términos de voltaje de corte, el transistor comienza con\(V_{CEQ}\) y\(I_{CQ}\). El mayor\(v_{CE}\) incremento que puede ocurrir es si la corriente cae a cero. Entonces, todo el potencial originalmente desarrollado a través\(r_E\) y\(r_C\) por\(I_{CQ}\) debe ser absorbido por el transistor. Por lo tanto
\[v_{CE (cutoff )} = V_{CEQ} +I_{CQ} (r_E+r_C ) \label{8.2} \]
Hay tres formas posibles de configurar esto: punto Q más cercano a la saturación, punto Q más cercano al corte o punto Q centrado en la línea de carga de CA. Consideremos primero el punto Q más cerca de la saturación. Esto se muestra en la Figura\(\PageIndex{3}\).
Aquí hemos trazado el voltaje de entrada en rojo y dibujado la corriente de colector correspondiente y el voltaje colector-emisor en azul. Es evidente que a medida que aumenta la señal de entrada, eventualmente, la señal de salida se limita a cero para\(v_{CE}\) y a\(i_{C(sat)}\) para\(i_C\). Las dos formas de onda azules están severamente recortadas y distorsionadas. La oscilación de voltaje pico no recortada más grande es\(V_{CEQ}\) y la oscilación de corriente máxima más grande es\(i_{C(sat)} − I_{CQ}\), o más convenientemente,\(V_{CEQ}/(r_E+r_C)\).
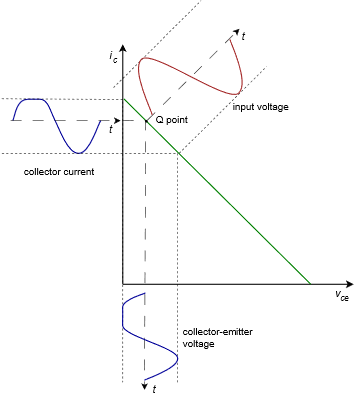
Figura\(\PageIndex{3}\): Línea de carga AC, punto Q más cercano a la saturación.
Si desplazamos el punto Q hacia el punto de corte, resolvemos el problema de recorte de saturación pero ahora tenemos un nuevo problema, como se ilustra en la Figura\(\PageIndex{4}\). No debería sorprendernos que ahora tengamos recorte de corte.
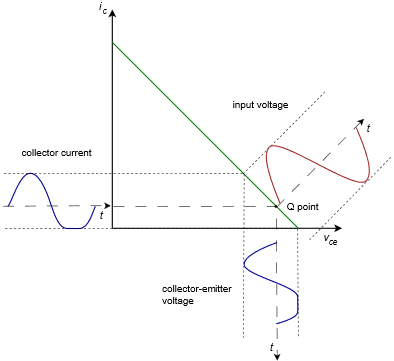
Figura\(\PageIndex{4}\): Línea de carga de CA, punto Q más cerca del corte.
En esta versión, la mayor oscilación de voltaje pico sin recortar es\(v_{CE(cutoff)} − V_{CEQ}\) (o alternativamente,\(I_{CQ}(r_E+r_C))\) y la oscilación de corriente máxima más grande es\(I_{CQ}\). Lo importante aquí es que la forma de onda haya sido recortada. Realmente no importa qué lado se haya recortado, de cualquier manera es una distorsión burda. Eventualmente, cada amplificador tendrá un límite pero podremos producir la mayor oscilación de voltaje sin recortar si el punto Q está centrado en la línea de carga de CA. Esto se muestra en la Figura\(\PageIndex{5}\).
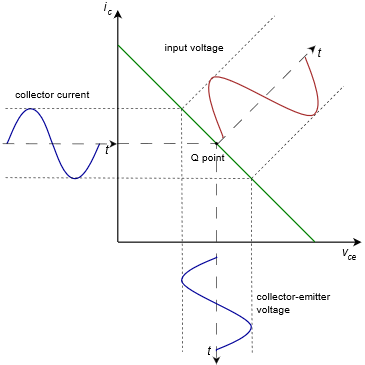
Figura\(\PageIndex{5}\): Línea de carga AC, punto Q centrado.
Con un punto Q centrado, la oscilación de voltaje pico no recortada más grande es\(V_{CEQ}\) y la oscilación de corriente máxima no recortada más grande es\(I_{CQ}\). Al examinar las ecuaciones\ ref {8.1} y\ ref {8.2} es evidente que para lograr un punto Q centrado en la línea de carga de CA, debe ser cierto lo siguiente:
\[\frac{V_{CEQ}}{I_{CQ}} = r_E+r_C \label{8.3} \]
Por supuesto, si bien es útil determinar el voltaje máximo a través del transistor, es más importante determinar el voltaje máximo a través de la carga. Mirando hacia atrás en el circuito de la Figura\(\PageIndex{1}\), la mayoría de las veces la tensión de carga máxima (es decir, la conformidad) será igual a la tensión máxima del transistor. Este será el caso en seguidores de voltaje y amplificadores no inundados. La única vez que habrá una reducción notable es con amplificadores muy inundados. En este caso el cumplimiento será reducido por el divisor de voltaje entre las resistencias de carga y de pantano. Por ejemplo, un amplificador inundado con una ganancia de voltaje de 4 perdería alrededor del 20% del swing máximo. El pantano tiene que ser muy pesado, lo que resulta en ganancias muy bajas antes de que se pierda una señal apreciable.
Así llegamos a la siguiente regla general:
\[\text{Peak compliance is the smaller of } V_{CEQ} \text{ or } I_{CQ}(r_E+r_C) \label{8.4} \]
Conociendo el cumplimiento, la potencia de carga máxima se puede determinar usando la ley de potencia. La potencia se determina usando valores RMS, por lo que el cumplimiento máximo deberá dividirse por\(\sqrt{2}\) (o multiplicarse por 0.707) antes de continuar.
\[P_{load (max)} = \frac{{Compliance_{RMS}}^2}{R_L} \label{8.5} \]
Hay algo importante a tener en cuenta sobre esta ecuación. Utiliza el valor de resistencia de carga, no el valor efectivo de CA total (es decir, no\(r_L\) que está\(R_L\) en paralelo con una resistencia de polarización). Si\(r_L\) se usara, estaríamos calculando la potencia en la carga más la potencia en la resistencia de polarización.
También nos gustaría determinar la potencia máxima disipada por el transistor. Debido a que la corriente y el voltaje del transistor fluctúan con la señal de entrada, necesitamos determinar la magnitud de la tensión de carga que produce la máxima potencia en el transistor. Intuitivamente, podríamos adivinar que esto ocurre a la máxima potencia de carga pero resulta que esta suposición es incorrecta. En condiciones de ausencia de señal, el transistor está funcionando estáticamente en el punto Q. Por lo tanto, la disipación de potencia en reposo es
\[P_{DQ} = V_{CEQ} I_{CQ} \label{8.6} \]
En contraste, a plena carga para un punto Q centrado, tenemos
\[v_{CE} = V_{CEQ} (1− \sin 2 \pi ft) \nonumber \]
\[i_C = I_{CQ} (1+ \sin 2 \pi ft) \nonumber \]
\[P_D = v_{CE} i_C \\ P_D = V_{CEQ} (1− \sin 2 \pi ft) \times I_{CQ} (1+ \sin 2 \pi ft) \\ P_D = V_{CEQ} I_{CQ} (1− \sin^2 2 \pi ft) \\ P_D = V_{CEQ} I_{CQ} (.5+.5 \cos 4 \pi ft) \\ P_D = \frac{P_{DQ}}{2} + \frac{P_{DQ}}{2} \cos 4 \pi ft \label{8.7} \]
El primer término de la Ecuación\ ref {8.7} es un desplazamiento fijo mientras que el segundo término es una sinusoide al doble de la frecuencia de la señal. Debido a que la amplitud máxima de esta sinusoide es la misma que el desplazamiento fijo, el promedio a lo largo del tiempo es simplemente el valor de desplazamiento. Estas formas de onda se ilustran en la Figura\(\PageIndex{6}\).
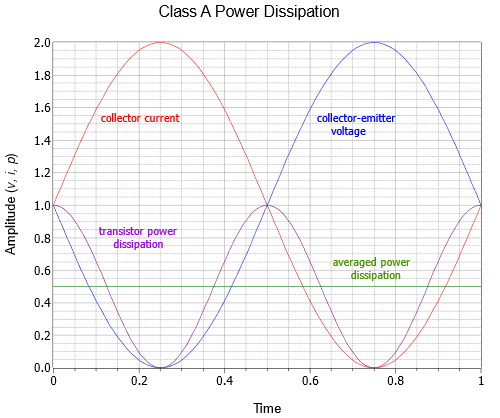
Figura\(\PageIndex{6}\): Disipación de potencia del transistor a plena carga.
El resultado es que el transistor solo disipa la mitad de la potencia a plena carga que disipa en condiciones de ralentí. Esto tiene mucho sentido si se detiene a considerar que el amplificador de clase A siempre extrae la misma potencia de las fuentes de CC, independientemente del tamaño de la señal de carga. Sin recorte, la corriente promedio será\(I_{CQ}\). Esa corriente multiplicada por el voltaje de suministro produce la potencia suministrada. Lo que sucede es que a medida que la señal aumenta en amplitud, cada vez más de la potencia disipada por el transistor se desplaza a la carga. En la oscilación de carga máxima, tanto el transistor como la carga se disiparán\(P_{DQ}/2\). Por extraño que pueda parecer, si quieres mantener fresco el transistor de salida de un amplificador de clase A, no bajes el volumen, subirlo.
Lo anterior implica que los diseños de clase A no son energéticamente eficientes. Esta es efectivamente la situación. Como acabamos de ver, el mejor de los casos la potencia máxima de carga será la mitad de\(P_{DQ}\), asumiendo un punto Q centrado (no centrado será peor). Para lograr esta oscilación, la fuente de alimentación tendrá que ser al menos dos veces más grande que\(V_{CEQ}\) porque tiene que cubrir la oscilación pico a pico, mientras que\(V_{CEQ}\) representa la oscilación pico para un punto Q centrado. 1 En todo caso, el mejor de los casos la eficiencia resulta ser pésima, de la siguiente manera.
\[\eta = \frac{P_{out}}{P_{i n}} = \frac{P_{load}}{P_{DC}} \nonumber \]
\[\eta = \frac{P_{DQ} /2}{2V_{CEQ} I_{CQ}} \nonumber \]
\[\eta = \frac{P_{DQ} / 2}{2 P_{DQ}} \nonumber \]
\[\eta = 25 \% \nonumber \]
Esto representa la máxima o mejor eficiencia de caso para un amplificador de clase A\(RC\) acoplado. Puede ser considerablemente menor dependiendo precisamente de cómo esté sesgada. Esto, verdaderamente, es el talón de Aquiles de la topología de clase A: es derrochador. Extrae toda la potencia de la fuente independientemente de si la señal está presente y, en el mejor de los casos, traducirá solo una cuarta parte de esa energía en potencia de carga útil. Al mismo tiempo, la disipación de potencia del transistor deberá ser al menos el doble de la potencia de carga entregada, y podría necesitar ser mucho mayor. ¿Por qué usarlo entonces? En su beneficio, es un diseño relativamente simple por lo que si no se necesitan grandes potencias de salida, puede resultar útil. Este es definitivamente el caso de las primeras etapas de un amplificador multietapa donde la cantidad de potencia de carga es muy pequeña (básicamente la potencia entregada a la siguiente etapa). En ese caso, la mayor complejidad de diseños con mayor eficiencia energética no está justificada ni es rentable.
Ejemplo\(\PageIndex{1}\)
Para el amplificador mostrado en la Figura\(\PageIndex{7}\), determine el cumplimiento, la potencia de carga máxima, la disipación del transistor en el peor de los casos y la eficiencia
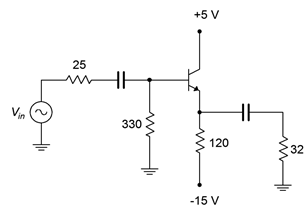
Figura\(\PageIndex{7}\): Esquema por ejemplo\(\PageIndex{1}\).
\[I_{CQ} = \frac{∣V_{EE}∣−V_{BE}}{R_E} \nonumber \]
\[I_{CQ} = \frac{15 V−0.7 V}{120 \Omega} \nonumber \]
\[I_{CQ} = 119mA \nonumber \]
Por inspección,\(V_{CEQ}\) = 5.7 V. El voltaje de corte de CA es
\[v_{CE (cutoff )} = V_{CEQ} +I_{CQ} (r_C+r_E ) \nonumber \]
\[v_{CE (cutoff )} = 5.7 V+119mA(0+120 \Omega || 32 \Omega ) \nonumber \]
\[v_{CE (cutoff )} = 5.7 V+119mA(25.3 \Omega ) \nonumber \]
\[v_{CE (cutoff )} = 5.7 V+3V \nonumber \]
\[v_{CE (cutoff )} = 8.7 V \nonumber \]
El más pequeño de\(V_{CEQ}\) y\(I_{CQ}(r_C+r_E)\) es el cumplimiento máximo, por lo que
\[compliance = 3 V peak \nonumber \]
Dado el cumplimiento, podemos usar la ley de energía para encontrar la potencia de carga
\[P_{load (max)} = \frac{{Compliance_{RMS}}^2}{R_L} \nonumber \]
\[P_{load (max)} = \frac{(.707 \times 3 V)^2}{32 \Omega} \nonumber \]
\[P_{load (max)} = 141mW \nonumber \]
Esto no es mucha potencia para algo así como un altavoz pero es una buena cantidad para manejar algo así como un par de auriculares.
La disipación de potencia del peor caso del transistor es
\[P_{D (max)} = P_{DQ} = I_{CQ} V_{CEQ} \nonumber \]
\[P_{D (max)} = 119mA \times 5.7V \nonumber \]
\[P_{D (max)} = 678mW \nonumber \]
La potencia del circuito suministrado es el consumo de corriente promedio multiplicado por el diferencial de voltaje total suministrado
\[P_{DC} = I_{CQ} (V_{CC} −V_{EE}) \nonumber \]
\[P_{DC} = 119mA \times 20 V \nonumber \]
\[P_{DC} = 2.38W \nonumber \]
La eficiencia es la relación entre la potencia de carga máxima y la alimentación de CC suministrada
\[\eta = \frac{P_{load (max )}}{P_{DC}} \nonumber \]
\[\eta = \frac{141mW}{2.38 W} \nonumber \]
\[\eta = 5.9 \% \nonumber \]
Esto es mucho peor que el mejor caso teórico. Esto se debe, al menos en parte, a que el punto Q no está centrado en la línea de carga de CA.
Para completar el análisis, tenga en cuenta que la clasificación de ruptura del transistor (\(BV_{CEO}\)) debe ser al menos tan grande como\(v_{CE(cutoff)}\) (8.7 voltios), y la clasificación de corriente máxima debe ser al menos tan grande como\(i_{C(sat)}\) (119 mA+5.7 V/25.3\( \Omega \) = 344 mA).
Simulación por Computadora
A continuación se examina una simulación por computadora de un seguidor de emisor de clase A usando un par Darlington. De interés primordial aquí es la verificación del cumplimiento de la salida por lo que se utilizará un análisis transitorio. El esquema del simulador se muestra en la Figura\(\PageIndex{8}\).
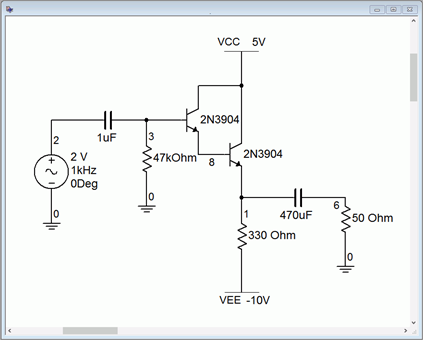
Figura\(\PageIndex{8}\): Seguidor Clase A en simulador.
Podemos hacer algunos cálculos rápidos para determinar el cumplimiento. Primero, encontramos la corriente del punto Q del colector.
\[I_{CQ} = \frac{∣V_{EE}∣−V_{BE}}{R_E} \nonumber \]
\[I_{CQ} = \frac{10 V−1.4 V}{330 \Omega} \nonumber \]
\[I_{CQ} = 26mA \nonumber \]
Por inspección, el emisor es de dos potenciales de unión base-emisor bajo tierra, o −1.4 V. Como los colectores están atados a\(V_{CC}\), esto significa que\(V_{CEQ}\) = 6.4 V. La otra mitad de la oscilación, de\(V_{CEQ}\) a\(v_{CE(cutoff)}\) es
\[v_{CE (cutoff )}−V_{CEQ} = I_{CQ}(r_C+r_E ) \nonumber \]
\[v_{CE (cutoff )}−V_{CEQ} = 26mA(0+330 \Omega || 50 \Omega ) \nonumber \]
\[v_{CE (cutoff )}−V_{CEQ} = 26mA( 43.4 \Omega ) \nonumber \]
\[v_{CE (cutoff )}−V_{CEQ} = 1.13V \nonumber \]
El punto Q no está centrado y está más cerca del punto de corte. Esto significa que el amplificador producirá recortes de corte alrededor de 1.1 voltios y saturación recortando alrededor de 6 voltios. En otras palabras, hay más espacio para que la corriente oscile hasta la saturación que para descender a cero. Como esta es la corriente que fluye a través de la carga y tenemos un seguidor no inversor, esperamos que el voltaje de carga haga eco de esto. Es decir, la porción negativa de la tensión de carga debe acortarse antes que la porción positiva.
Los resultados del análisis transitorio se muestran en la Figura\(\PageIndex{9}\). Se aplica una señal de entrada de pico de dos voltios (traza azul). La porción negativa de la tensión de carga se acorta a aproximadamente 1.1 voltios como se esperaba (traza roja). La señal de entrada no es lo suficientemente grande como para provocar un recorte de saturación. Esto se hizo a propósito para verificar la ganancia de voltaje del seguidor. Debe estar muy cerca de la unidad. De hecho, la traza muestra que la ganancia es de alrededor de 0.95 o así.
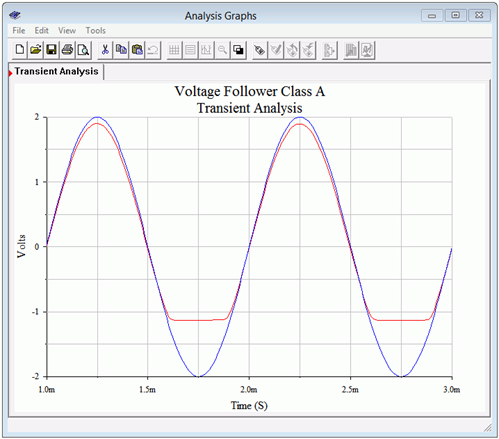
Figura\(\PageIndex{9}\): Análisis transitorio de seguidor de clase A.
Si esto hubiera sido un amplificador de voltaje en lugar de un seguidor, estas formas de onda aparecerían volteadas verticalmente. Para verificar esto, se modifica el circuito para producir un amplificador de voltaje con una ganancia de aproximadamente uno. Esto se logra moviendo la carga al colector y agregando una resistencia de\( \Omega \) polarización 330. Esto dará como resultado la misma impedancia de carga de CA. Para mantener un similar\(V_{CEQ}\),\(V_{CC}\) se eleva en 10 voltios. Finalmente, la resistencia de polarización\( \Omega \) del emisor 330 original se divide en dos: 287\( \Omega \) y 43\( \Omega \). Esto cederá lo mismo\(I_{CQ}\) y logrará una ganancia de voltaje de unidad. Como resultado, esperamos ver recortes a aproximadamente 1.1 voltios en la porción positiva. El circuito modificado se muestra en la Figura\(\PageIndex{10}\) y la simulación transitoria resultante en la Figura\(\PageIndex{11}\).
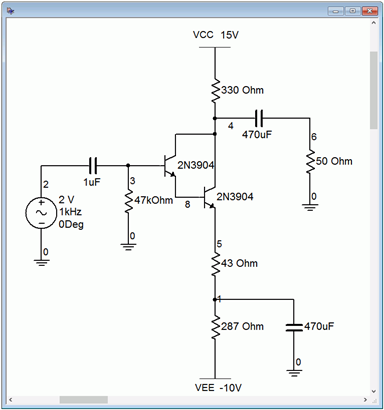
Figura\(\PageIndex{10}\): Amplificador Clase A en simulador.
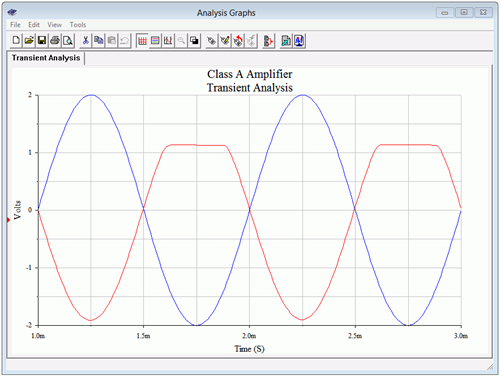
Figura\(\PageIndex{11}\): Análisis transitorio de amplificador de clase A.
Un último elemento de interés respecto a las simulaciones: Si el nivel de entrada se incrementa en un intento de ver recorte en la otra mitad de la forma de onda, sucede algo extraño. Al principio aparecerá como si nunca se acortara. Sin embargo, un examen cuidadoso revela algo diferente. Dados los valores en estos circuitos, exhibirán cierta cantidad de acción de sujeción (el pinzamiento se presentó en el Capítulo 3). Esto hará que la forma de onda se desvía. Si inspecciona el valor de pico a pico, estará cerca del valor de\(v_{CE(cutoff)}\). Será un poco menos debido a que, particularmente para un par Darlington, no\(V_{CE(sat)}\) es 0 V.
Referencias
1 Este es el caso si las líneas de carga de CA y CC son idénticas. Esto es atípico. En consecuencia, la fuente de alimentación tenderá a ser mayor del doble,\(V_{CEQ}\) lo que empeora aún más la situación.


