8.6: Disipadores de calor

El problema con los transistores de potencia es siempre el calor. Como se señala en el Ejemplo 8.5.1, a medida que el transistor se calienta debido a la disipación de potencia interna, su capacidad para disipar el calor se ve comprometida. El truco, entonces, es mover de manera eficiente el calor del transistor a otro lugar. Esto se logra normalmente mediante el uso de un disipador de calor.

Un disipador de calor es un dispositivo de metal que está conectado al transistor de potencia. Por lo general, están hechos de aluminio y cuentan con una variedad de aletas. Al aumentar el área de superficie, el calor se puede alejar del transistor de manera más eficiente que solo por el transistor.

Los disipadores de calor están diseñados para montar estilos específicos de cajas de dispositivos. Los estilos de caja más comunes incluyen la “lata” TO-3 junto con los diversos estilos de “pestaña eléctrica” como el TO-220 y el TO-202. También se requieren herrajes de montaje especiales y espaciadores de aislamiento para mantener el aislamiento eléctrico entre el transistor y el disipador de calor, ya que no queremos que el disipador de calor esté eléctricamente vivo. Esto generalmente toma la forma de una lámina de mica, y arandelas y casquillos de plástico para los tornillos de la máquina de montaje (para disipadores de calor pequeños, a veces se utilizan tornillos de nylon para máquinas).

Hay algunas reglas generales que deben seguirse al usar disipadores de calor:

• Siempre use algún tipo de grasa para disipadores de calor o almohadilla térmicamente conductora entre el disipador de calor y el dispositivo. Esto aumentará la transferencia térmica entre las dos partes, sin embargo, cantidades excesivas de grasa disipadora de calor disminuirán el rendimiento.
• Monte las aletas en el plano vertical para un enfriamiento convectivo natural óptimo.
• No abarrote ni obstruya los dispositivos que utilizan disipadores de calor.
• No bloquee el flujo de aire alrededor de los disipadores de calor, especialmente directamente encima y debajo de los elementos que dependen de la convección natural.
• Si las demandas térmicas son particularmente altas, considere usar convección forzada (es decir, un pequeño ventilador dirigido al disipador de calor).

A continuación se muestran algunos disipadores de calor típicos. La figura\(\PageIndex{1}\) muestra un disipador de calor y una gráfica de datos térmicos para su uso con un solo dispositivo de caja TO-3.

Figura\(\PageIndex{1}\): Disipador de calor para TO-3. Reimpreso cortesía de Aavid Thermalloy, Inc.

La figura\(\PageIndex{2}\) muestra un disipador de calor diseñado para un par de transistores usando cajas TO-220. En esta foto, las almohadillas aislantes blancas se pueden ver entre los transistores y el disipador de calor.

Figura\(\PageIndex{2}\): Disipador de calor para doble TO-220. Reimpreso cortesía de Aavid Thermalloy, Inc.

8.6.1: Resistencia térmica

Para especificar un disipador de calor particular para una aplicación determinada, se encuentra en orden una explicación más técnica. Lo que vamos a hacer es crear un circuito térmico equivalente. En este modelo se emplea el concepto de resistencia térmica. La resistencia térmica denota lo fácil que es transferir energía térmica de una parte mecánica a otra. El símbolo de resistencia térmica es\(\theta \), y las unidades son grados Celsius por vatio. En este modelo, la temperatura es análoga a la tensión, y la disipación de potencia térmica es análoga a la corriente. Una ecuación útil es,

\[P_D= \frac{\Delta T}{\theta_{total}} \label{8.9} \]

Dónde\(P_D\) está la potencia disipada por el dispositivo semiconductor en vatios,\(\Delta T\) es el diferencial de temperatura, y\(\theta_{total}\) es la suma de las resistencias térmicas. Básicamente, esta es una versión térmica de la ley de Ohm.

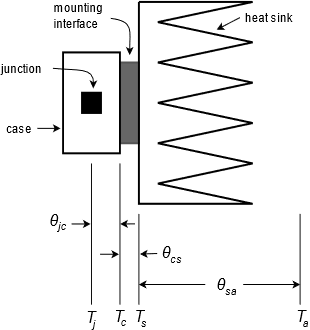
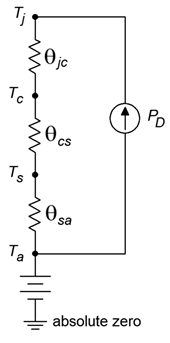
Para construir nuestro modelo, echemos un vistazo más de cerca a la combinación de dispositivo-potencia/disipador de calor. Esto se muestra en la Figura\(\PageIndex{3}\). El subíndice\(j\) significa unión,\(c\) es para caso (del transistor),\(s\) es para disipador de calor y a es para el aire ambiente. \(T_j\)es la temperatura de unión del semiconductor y es creada por el producto de la corriente y voltaje del transistor. Esta fuente térmica calienta la carcasa del dispositivo a\(T_c\). La resistencia térmica entre las dos entidades es\(\theta_{jc}\). El estuche, a su vez, calienta el disipador de calor a través de la interconexión. Esta resistencia térmica es\(\theta_{cs}\), y la temperatura resultante es\(T_s\). Finalmente, el disipador de calor pasa la energía térmica al aire circundante en el que se encuentra sentado\(T_a\). La resistencia térmica del disipador de calor al aire es\(\theta_{sa}\). El modelo térmico equivalente se muestra en la Figura\(\PageIndex{4}\). Si bien este “circuito térmico” no tiene una correspondencia perfecta con el análisis normal del circuito, sí ilustra los puntos principales.

Figura\(\PageIndex{3}\): Dispositivo y disipador de calor.

Figura\(\PageIndex{4}\): Modelo térmico equivalente de la Figura\(\PageIndex{3}\).

En este modelo, el suelo representa una temperatura de cero absoluto. El circuito está sentado a temperatura ambiente\(T_a\), por lo que una fuente de voltaje de\(T_a\) está conectada a tierra y al disipador de calor. Las tres resistencias térmicas están en serie y son impulsadas por una fuente de corriente que es establecida por la actual disipación de potencia del dispositivo. Tenga en cuenta que si la disipación de potencia es alta, las “caídas de voltaje” resultantes a través de las resistencias térmicas son altas. El voltaje es análogo a la temperatura en este modelo, por lo que esto indica que se crea una temperatura alta. Debido a que hay un límite máximo a\(T_j\), una disipación de potencia más alta requiere resistencias térmicas más bajas. Como\(\theta_{jc}\) establece el fabricante del dispositivo, no tenemos control sobre ese elemento. Sin embargo,\(\theta_{cs}\) es una función del estilo de la caja y del material aislante utilizado, por lo que sí tenemos cierto control (pero no mucho) sobre eso. Por otro lado, como la persona que especifica el disipador de calor, tenemos mucho control sobre\(\theta_{sa}\). Los valores para\(\theta_{sa}\) son dados por los fabricantes de disipadores de calor. Una variación útil de la ecuación\ ref {8.9} es

\[P_D= \frac{T_j−T_a}{\theta_{jc}+\theta_{cs}+\theta_{sa}} \label{8.10} \]

Normalmente, la disipación de potencia, la unión y las temperaturas ambiente,\(\theta_{jc}\) y\(\theta_{cs}\) son conocidas. La idea es determinar un disipador de calor apropiado. Ambos\(T_j\) y\(\theta_{jc}\) son dados por el fabricante del dispositivo semiconductor. La temperatura ambiente,\(T_a\), puede determinarse experimentalmente. Debido al calentamiento localizado, tiende a ser mayor que la “temperatura ambiente” real. Para determinar se pueden utilizar gráficas estándar\(\PageIndex{5}\), como las que se encuentran en la Figura\(\theta_{cs}\). Tenga en cuenta los valores generalmente más bajos de\(\theta_{cs}\) para el caso TO-3 en relación con el TO-220. Esta es una de las razones por las que las cajas TO-3 se utilizan para dispositivos de mayor potencia. Este estuche también hace que sea más fácil para el fabricante reducir\(\theta_{jc}\).

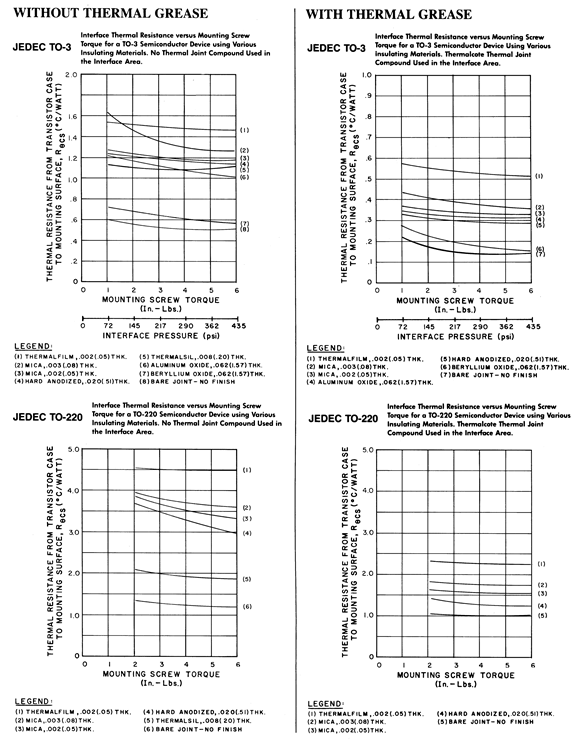
Figura\(\PageIndex{5}\):\(\theta_{CS}\) para TO-3 y TO-220 Reimpreso cortesía de Thermalloy, Inc.

Ejemplo\(\PageIndex{1}\)

Determine la clasificación de disipador de calor apropiada para un dispositivo de potencia nominal de la siguiente manera:\(T_{j(max)}\) = 175\(^{\circ}\) C, estilo de caja TO-3,\(\theta_{jc}\) = 1.5 C\(^{\circ}\) /W. El dispositivo disipará un máximo de 15 W en una temperatura ambiente de 40\(^{\circ}\) C. Supongamos que el disipador de calor se montará con disipador de calor grasa y un aislante de mica 0.002.

Primero, busque\(\theta_{cs}\) de la gráfica TO-3 “Con grasa térmica” en la Figura\(\PageIndex{5}\). Se utiliza la curva 3. El valor aproximado es de 0.35\(^{\circ}\) C/W.

\[P_D= \frac{T_j −T_a}{\theta_{jc}+\theta_{cs}+\theta_{sa}} \nonumber \]

\[\theta_{sa}= T j −Ta P D −\theta jc−\theta cs \nonumber \]

\[\theta_{sa}= \frac{175^{\circ}C −40^{\circ}C}{15 W} −1.5C^{\circ}/W −0.35C^{\circ}/W \nonumber \]

\[\theta_{sa}=7.15C^{\circ}/W \nonumber \]

Este es el valor máximo aceptable para la resistencia térmica del disipador de calor. Tenga en cuenta que el uso de grasa disipadora de calor nos da un extra de 0.8\(^{\circ}\) C/W más o menos. Para esta aplicación,\(\PageIndex{1}\) lo más probable es que el disipador de calor que se muestra en la Figura sea suficiente sin enfriamiento por aire forzado agregado (el gráfico se detiene a menos de 4\(^{\circ}\) C/W con un flujo de aire de menos de 200 pies/minuto).

Si repetimos este problema con un mucho más alto\(P_D\), las cosas salen un poco diferente. Usemos 40 W esta vez.

\[P_D= \frac{T_j −T_a}{\theta_{jc}+\theta_{cs}+\theta_{sa}} \nonumber \]

\[\theta_{sa}= \frac{T_j −T_a}{P_D} −\theta_{jc}−\theta_{cs} \nonumber \]

\[\theta_{sa}= \frac{175^{\circ}C −40^{\circ}C}{40 W} −1.5C^{\circ}/W −0.35C^{\circ}/W \nonumber \]

\[\theta_{sa}=1.53C^{\circ}/W \nonumber \]

Si esperamos usar ese mismo disipador de calor, tendremos que agregar enfriamiento por aire forzado de al menos 700 pies/minuto. La otra opción sería encontrar un disipador de calor más eficiente térmicamente (y probablemente mucho más grande) si esperamos usar solo la convección natural.