10.4: sesgo JFET
- Page ID
- 83399
Hay varias formas diferentes de sesgar un JFET. Para muchas configuraciones,\(I_{DSS}\) y\(V_{GS(off)}\) será necesario. Una forma sencilla de medir estos parámetros en el laboratorio se muestra en la Figura\(\PageIndex{1}\). Para medir simplemente\(I_{DSS}\) conectamos a tierra los terminales de puerta y fuente ya que esto obliga\(V_{GS}\) a ser 0 V. Insertamos un amperímetro entre\(V_{DD}\) y el drenaje, y luego establecemos\(V_{DD}\) a un valor superior a\(V_P\) (+15 VCC generalmente siendo suficiente). La lectura del amperímetro resultante es\(I_{DSS}\). Obtención\(V_{GS(off)}\) es sólo un poco más de trabajo. Dejando el amperímetro en el desagüe, desenganche la compuerta de tierra y en su lugar conéctelo a una fuente de alimentación negativa ajustable. Girar el suministro más negativo hasta que el amperímetro lea cero (prácticamente hablando, < 1% de\(I_{DSS}\)). En ese punto la fuente de voltaje será igual a\(V_{GS(off)}\).
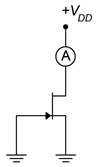
Figura\(\PageIndex{1}\): Medición\(I_{DSS}\) y\(V_{GS(off)}\).
10.4.1: Modelo DC
Antes de comenzar a examinar los propios circuitos de polarización, necesitamos un modelo básico de CC del JFET. En la Figura se muestra un modelo suficiente para nuestros análisis\(\PageIndex{2}\).
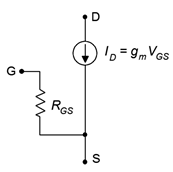
Figura\(\PageIndex{2}\): Modelo DC de JFET.
El modelo consiste en una fuente de corriente controlada por voltaje\(I_D\),, que es igual al producto de la tensión puerta-fuente,\(V_{GS}\), y la transconductancia,\(g_m\). La resistencia entre la puerta y la fuente\(R_{GS}\),, es la de la unión PN con polarización inversa, es decir, idealmente infinito para DC. Como consecuencia, en la mayoría de los circuitos prácticos podemos suponer que la corriente de puerta,\(I_G\), es cero. Por lo tanto,\(I_D = I_S\).
10.4.2: Polarización de voltaje constante
La forma más simple de polarización es la polarización de voltaje constante. El prototipo se muestra en la Figura\(\PageIndex{3}\) con direcciones de corriente y polaridades de voltaje mostradas.
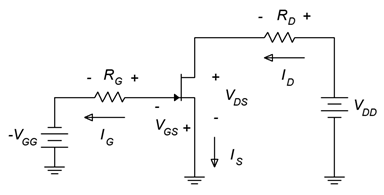
Figura\(\PageIndex{3}\): Prototipo de polarización de voltaje constante.
Este es un diseño bastante sencillo que utiliza solo un par de resistencias y fuentes de energía. La figura\(\PageIndex{4}\) muestra el mismo circuito pero con el modelo JFET insertado, listo para el análisis.
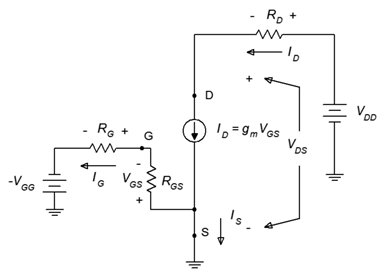
Figura\(\PageIndex{4}\): Polarización de voltaje constante con modelo.
En última instancia, el objetivo aquí es determinar un medio para encontrar la corriente de drenaje del transistor y el voltaje de la fuente de drenaje, junto con los potenciales a través de cualquier otro componente.
Para comenzar, considere el bucle puerta-fuente. Por KVL, la\(V_{GG}\) fuente debe caer a través\(R_G\) y la unión puerta-fuente,\(V_{GS}\).
\[V_{G G} = V_{R_G} +V_{GS} \nonumber \]
\[V_{G G} = I_G R_G+V_{GS} \nonumber \]
\(I_G\)es aproximadamente cero así que esto simplifica a
\[V_{GS} = V_{G G} \nonumber \]
Dada la transconductancia\(g_m\),, podemos encontrar\(I_D\). Como alternativa, se\(I_D\) puede encontrar usando la Ecuación 10.2.1 junto con los parámetros del dispositivo\(I_{DSS}\) y\(V_{GS(off)}\). Para este circuito, esta última técnica tiende a ser más práctica. Una vez que\(I_D\) se encuentra, se\(R_D\) puede encontrar la caída de voltaje a través, y luego\(V_{DS}\) se determina a partir de KVL.
Ejemplo\(\PageIndex{1}\)
Para el circuito de la Figura\(\PageIndex{5}\), determinar\(I_D\) y\(V_{DS}\). Supongamos\(I_{DSS}\) = 10 mA y\(V_{GS(off)}\) = −5 V.
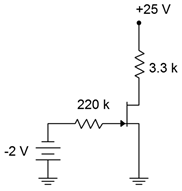
Figura\(\PageIndex{5}\): Esquema por ejemplo\(\PageIndex{1}\).
Primero, porque\(I_G \approx 0\), la caída a través\(R_G\) es\(\approx 0\) y\(V_{GS} = V_{GG}\). Usando la Ecuación 10.2.1
\[I_D = I_{DSS} \left( 1 − \frac{V_{GS}}{V_{GS (off )}} \right)^2 \nonumber \]
\[I_D = 10 mA \left( 1 − \frac{−2 V}{−5V} \right)^2 \nonumber \]
\[I_D = 3.6 mA \nonumber \]
Mirando el bucle dren-fuente, KVL muestra
\[V_{DD} = I_D R_D +V_{DS} \nonumber \]
\[V_{DS} = V_{DD} −I_D R_D \nonumber \]
\[V_{DS} = 25V −3.6mA \times 3.3k \Omega \nonumber \]
\[V_{DS} = 13.1 V \nonumber \]
Si bien el cálculo para la polarización de voltaje constante es relativamente simple, no presenta un punto Q estable. Por ejemplo, si Ejemplo\(\PageIndex{1}\) se repite con otro JFET, éste con\(I_{DSS}\) = 12 mA y\(V_{GS(off)}\) = −6 V, los resultados son radicalmente diferentes:\(I_D\) crece a 5.33 mA y\(V_{DS}\) se contrae a 7.4 V. Estos son cambios considerables dados los cambios relativamente modestos en los parámetros del dispositivo. En este sentido, la polarización de voltaje constante recuerda a la configuración de polarización de base simple utilizada con los BJT.
Para comprender mejor el problema de estabilidad del punto Q, consulte la Figura\(\PageIndex{6}\).
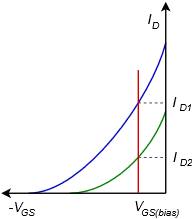
Figura\(\PageIndex{6}\): Variación para polarización de voltaje constante.
Aquí se trazan curvas características para dos dispositivos diferentes, uno en verde y otro en azul. Estos representan el tipo de variaciones de parámetros del dispositivo que podríamos esperar ver en un modelo de producto. El valor fijo del voltaje de polarización de la puerta se muestra en rojo. A partir de esta gráfica debería ser obvio que esta forma de polarización producirá una amplia variación en la corriente de drenaje, y por lo tanto, no es una buena opción para aplicaciones que requieren un punto Q estable. Si la aplicación no tiene este requisito, la polarización de voltaje constante ofrece la ventaja de requerir un mínimo de componentes.
10.4.3: Autosesgo
La autopolarización utiliza una pequeña cantidad de componentes y solo una sola fuente de alimentación, sin embargo, ofrece una mejor estabilidad que la polarización de voltaje constante. El nombre proviene del hecho de que la corriente de drenaje se utilizará para crear una caída de voltaje que configura la puerta-fuente, de ahí que el circuito “sesgue a sí mismo”. También se le conoce como sesgo automático. El prototipo de autosesgo se muestra en la Figura\(\PageIndex{7}\).
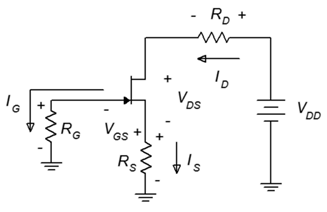
Figura\(\PageIndex{7}\): Prototipo de autosesgo.
Una vez más, podemos suponer que\(I_G\) es 0. Como\(R_G\) está conectado directamente a tierra, esto significa que\(V_G \approx 0\) V. Siendo esto cierto, la inspección del esquema revela que la magnitud de\(V_{GS}\) debe ser la misma que la tensión a través\(R_S\). Porque\(I_D = I_S\) entonces
\[V_{GS} = −I_D R_S \label{10.6} \]
Este valor de\(V_{GS}\) es lo que genera la corriente de drenaje. La definición es autorreferencial. Siendo este el caso, ¿cómo analizamos el circuito? Una derivación adecuada de la ecuación para la corriente de drenaje no es trivial. Comenzamos con la ecuación característica (Ecuación 10.2.1) y la expandimos.
\[I_D = I_{DSS}\left ( 1 − \frac{V_{GS}}{V_{GS (off )}} \right)^2 \nonumber \]
\[I_D = I_{DSS} \left( 1 − \frac{2V_{GS}}{V_{GS (off )}} + \frac{{V_{GS}}^2}{{V_{GS(off )}}^2} \right) \nonumber \]
\[I_D = I_{DSS} − \frac{2 I_{DSS} V_{GS}}{V_{GS (off )}} + \frac{I_{DSS} {V_{GS}}^2}{{V_{GS (off )}}^2} \nonumber \]
Sustituir usando la Ecuación 10.2.2
\[g_{m0} =− \frac{2 I_{DSS}}{V_{GS(off )}} \nonumber \]
\[I_D = I_{DSS} +g_{m0} V_{GS} + \frac{I_{DSS} {V_{GS}}^2}{{V_{GS (off )}}^2} \nonumber \]
Usando la ecuación\ ref {10.6} esto se puede expandir a
\[I_D = I_{DSS} −g_{m0} I_D R_S + \frac{I_{DSS} {I_D}^2 {R_S}^2}{{V_{GS (off )}}^2} \nonumber \]
Reordenación de los rendimientos
\[0 = \frac{I_{DSS} {R_S}^2}{{V_{GS (off )}}^2} {I_D}^2 − (1 +g_{m0} R_S )I_D +I_{DSS} \nonumber \]
Esta es una ecuación cuadrática en la forma\(ax^2+bx+c\) y se puede resolver usando la fórmula cuadrática:
\[y = \frac{−b\pm \sqrt{b^2−4ac}}{2a} \nonumber \]
La opción positiva en el numerador puede ser ignorada ya que esto ocurre para\(V_{GS}\) más allá\(V_{GS(off)}\). El resultado es
\[I_D = 2 I_{DSS} \left( \frac{1+g_{m0} R_S −\sqrt{1+2 g_{m0} R_S}}{( g_{m0} R_S )^2} \right) \label{10.7} \]
Aunque esta es una solución analítica precisa, ciertamente no es el tipo de ecuación que la mayoría de la gente quiere memorizar o derivar según sea necesario. Como el\(g_{m0} R_S\) término se repite en esta ecuación varias veces, es útil graficar esta ecuación en términos de normalizado\(I_D\) versus\(g_{m0} R_S\). Esta curva se grafica en la Figura\(\PageIndex{8}\).
Para utilizar esta curva, el primer paso es encontrar\(g_{m0} R_S\). El valor de\(R_S\) se determina por inspección y\(g_{m0}\) puede ser determinado por la Ecuación 10.2.2, repetida a continuación por conveniencia.
\[g_{m0} =− \frac{2 I_{DSS}}{V_{GS(off )}} \nonumber \]
El valor de\(g_{m0} R_S\) se encuentra en el eje horizontal, se traza hasta la curva y luego sobre la\(I_D\) relación normalizada. Este número se multiplica por\(I_{DSS}\) para determinar el valor de\(I_D\).
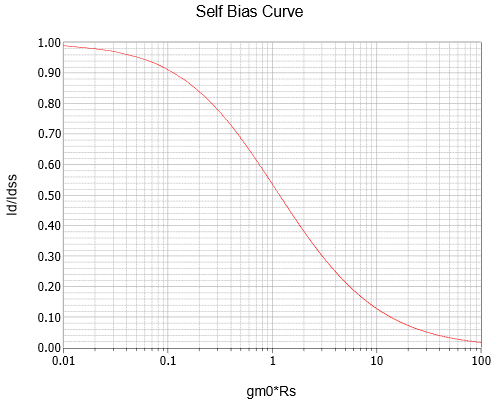
Figura\(\PageIndex{8}\): Curva de autosesgo.
Ejemplo\(\PageIndex{2}\)
Determine\(I_D\) y\(V_{DS}\) para el circuito que se muestra en la Figura\(\PageIndex{9}\). Supongamos\(I_{DSS}\) = 10 mA y\(V_{GS(off)}\) = −4 V.
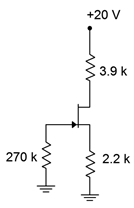
Figura\(\PageIndex{9}\): Esquema por ejemplo\(\PageIndex{2}\).
Usando el método gráfico, primero determine\(g_{m0} R_S\).
\[g_{m0} =− \frac{2 I_{DSS}}{V_{GS (off )}} \nonumber \]
\[g_{m0} =− \frac{2 \times 10 mA}{−4 V} \nonumber \]
\[g_{m0} = 5mS \nonumber \]
Por lo tanto\(g_{m0} R_S\) = 5 mS\(\cdot\) 2.2 k\(\Omega = 11\). El gráfico de autopolarización rinde aproximadamente 0.12 para la relación de corriente normalizada. Por lo tanto
\[I_D = 0.12 I_{DSS} \nonumber \]
\[I_D = 0.12 \times 10 mA \nonumber \]
\[I_D = 1.2mA \nonumber \]
Usando la ley de Ohm y KVL
\[V_D = V_{DD} −I_D R_D \nonumber \]
\[V_D = 20 V−1.2mA \times 3.9 k\Omega \nonumber \]
\[V_D = 15.32V \nonumber \]
\[V_S = I_D R_S \nonumber \]
\[V_S = 1.2mA \times 2.2 k\Omega \nonumber \]
\[V_S = 2.64 V \nonumber \]
\[V_{DS} = V_D −V_S \nonumber \]
\[V_{DS} = 15.32 V −2.64 V \nonumber \]
\[V_{DS} = 12.68 V \nonumber \]
Una técnica alternativa es hacer una suposición inicial para\(V_{GS}\), típicamente la mitad de\(V_{GS(off)}\). Luego\(I_D\) se calcula el valor de a partir de la ecuación característica (Ecuación 10.2.1) y se compara con la relación de ley de Ohm, Ecuación\ ref {10.6}, reescrita como\(I_D = −V_{GS}/R_S\). Lo más probable es que los dos resultados no estén de acuerdo así que ajusta la\(V_{GS}\) estimación y repite el proceso. Si se hace correctamente, las corrientes deben estar más cerca. Iterar este proceso hasta que converja en la respuesta.
Para usar esta técnica para el problema anterior comenzaríamos asumiendo\(V_{GS}\) = −2 V (la mitad de\(V_{GS(off)}\)). Usando esto en la Ecuación 10.2.1 rinde\(I_D\) = 2.5 mA, mientras que usando la Ecuación\ ref {10.6} produce\(I_D\) = 910\(\mu\) A. Obviamente la estimación inicial no fue correcta. La segunda estimación para\(V_{GS}\) las necesidades de aumentar negativamente ya que esto disminuirá el resultado de la Ecuación 10.2.1 y aumentará el resultado de la Ecuación\ ref {10.6}, ojalá se encuentre en el medio. Podríamos intentar −2.5 voltios. Esto dará 1.4 mA de la Ecuación 10.2.1 y 1.14 mA de la Ecuación\ ref {10.6}. A medida que la brecha se ha reducido, el ajuste para la tercera estimación será menor, por lo que podríamos intentar −2.6 voltios. Esto estaría relativamente cerca del valor calculado en Example\(\PageIndex{2}\) (\(V_{GS} = −V_S\)).
Esta técnica de aproximación también ofrece una pista sobre cómo la autopolarización gana estabilidad sobre la polarización de voltaje constante. Si por alguna razón\(I_D\) aumentara, esto crearía una caída de voltaje mayor a través\(R_S\). Debido a que este voltaje es de la misma magnitud que\(V_{GS}\), esto significa que\(V_{GS}\) crece negativamente. A más negativo se\(V_{GS}\) reduce\(I_D\), oponiéndose así al cambio inicial en la corriente de drenaje. Este mecanismo de retroalimentación es similar en función al sesgo de retroalimentación del colector BJT. El tema de estabilidad se visualiza en la Figura\(\PageIndex{10}\).
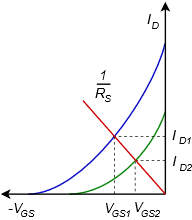
Figura\(\PageIndex{10}\): Variación por autosesgo.
Se trazan dos curvas de dispositivo para representar la variación de parámetros (verde y azul). La ecuación\ ref {10.6} muestra la relación entre\(I_D\) y\(V_{GS}\). Si ponemos esto en la forma\(y = mx + b\), nos encontramos con que la línea pasa por el origen y tiene una pendiente de\(1/R_S\). Esta línea está trazada en rojo. Donde la línea se cruza, la curva del dispositivo produce la corriente de drenaje y el voltaje puerta-fuente para ese dispositivo en particular. A diferencia de la polarización de voltaje constante, la autopolarización cambia alguna variación a\(V_{GS}\), lo que hace\(I_D\) más estable. De hecho, si hay un objetivo de diseño particular para\(I_D\) o\(V_{GS}\), se puede usar un reordenamiento de la Ecuación\ ref {10.6} para encontrar el valor necesario de\(R_S\) junto con la curva o ecuación característica.
\[R_S =− \frac{V_{GS}}{I_D} \nonumber \]
Por ejemplo, si\(I_D\) se desea un cierto, este valor podría usarse con la Ecuación 10.2.1 para determinar el correspondiente\(V_{GS}\). Estos valores se utilizan entonces para encontrar los requeridos\(R_S\). Como alternativa, los valores normalizados podrían obtenerse a través de la Figura 10.2.4.
Ejemplo\(\PageIndex{3}\)
Determine un valor\(R_S\) para establecer\(V_{GS}\) = −2 V para el circuito que se muestra en la Figura\(\PageIndex{11}\). Supongamos\(I_{DSS}\) = 20 mA y\(V_{GS(off)}\) = −4 V.
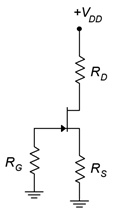
Figura\(\PageIndex{11}\): Esquema por ejemplo\(\PageIndex{3}\).
Podemos determinar la corriente de drenaje usando la Ecuación 10.2.1.
\[I_D = I_DSS \left( 1 − \frac{V_{GS}}{V_{GS (off )}} \right)^2 \nonumber \]
\[I_D = 20 mA \left( 1 − \frac{−2V}{−4V} \right)^2 \nonumber \]
\[I_D = 5 mA \nonumber \]
\[R_S =− \frac{V_{GS}}{I_D} \nonumber \]
\[R_S =− \frac{−2 V}{5mA} \nonumber \]
\[R_S = 400 \Omega \nonumber \]
En resumen, la autopolarización es un circuito de recuento mínimo de piezas que ofrece una estabilidad modesta. La estabilidad se puede mejorar con la adición de otros componentes, como veremos con la siguiente configuración de sesgo.
10.4.4: Sesgo combinado
La configuración de polarización combinada (AKA source bias) se basa en la autopolarización pero agrega una fuente de alimentación negativa conectada a\(R_S\), de ahí su nombre. Esto mejorará la estabilidad de\(I_D\),\(V_{DS}\) y\(g_m\). El prototipo de sesgo combinado se muestra en la Figura\(\PageIndex{12}\).
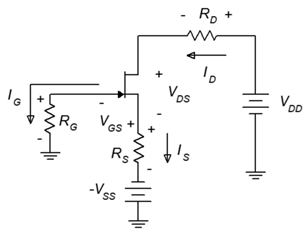
Figura\(\PageIndex{12}\): Prototipo de sesgo combinado.
El análisis es similar al de la autopolarización pero con un giro importante: la fuente de alimentación de la fuente aumenta la caída de voltaje a través de\(R_S\). Esto estabiliza el voltaje (y por lo tanto, la corriente) porque ya no es igual a\(−V_{GS}\), sino más bien
\[V_{R_S} = I_D R_S =∣V_{GS}∣+∣V_{SS}∣ \label{10.8} \]
Si\(V_{SS} \gg V_{GS}\), entonces podemos aproximarnos\(I_D\) como\(V_{SS}/R_S\). Al igual que con el autosesgo,\(I_D\) es posible una solución analítica para. Para ello, comenzaríamos con la ecuación característica y la Ecuación\ ref {10.8}. La derivación se deja como ejercicio.
\[I_D = 2 I_{DSS} \left( \frac{1+g_{m0} R_S (1+k )−\sqrt{1+2 g_{m0}R_S (1+k)}}{( g_{m0} R_S )^2} \right) \label{10.9} \]
La fórmula es muy similar a la fórmula de autosesgo pero con la adición de un factor,\(k\). \(k\)es un “factor de pantano” y se define como la relación de\(V_{SS}\) a\(V_{GS(off)}\). Si\(k = 0\), no hay fuente de alimentación y la fórmula vuelve a la fórmula de autopolarización más simple. Por otro lado, si\(k\) es muy grande,\(I_D \approx V_{SS}/R_S\).
Como fue el caso con el autosesgo, podemos trazar la Ecuación\ ref {10.9} usando el\(g_{m0}R_S\) factor. Una serie de tres parcelas para\(k\) = 2, 3 y 4 se renderizan en Figura\(\PageIndex{13}\). 1
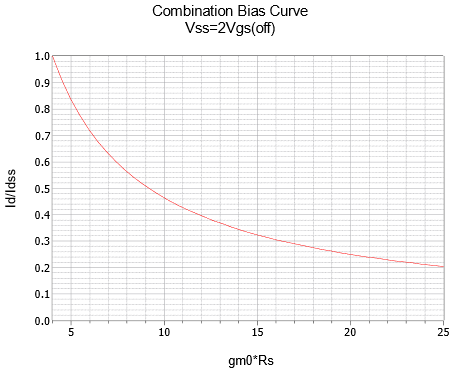
Figura\(\PageIndex{13a}\): Curva de sesgo combinada,\(k = 2\).
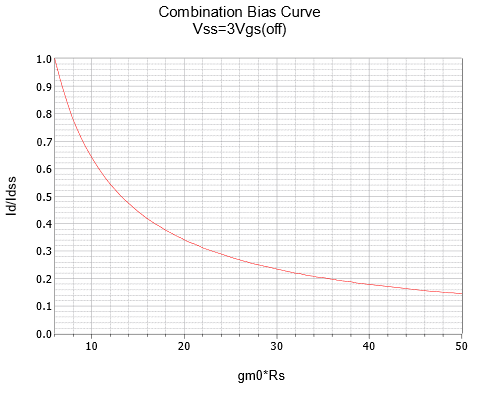
Figura\(\PageIndex{13b}\): Curva de sesgo combinada,\(k = 3\).
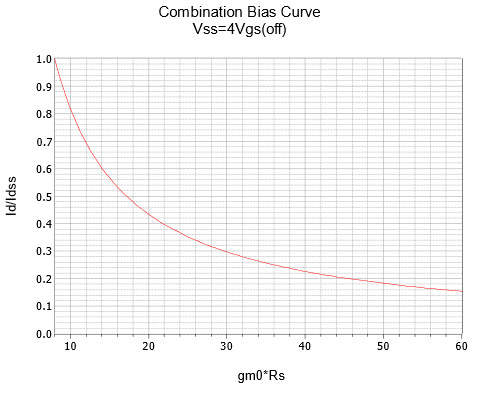
Figura\(\PageIndex{13c}\): Curva de sesgo combinada,\(k = 4\).
Ejemplo\(\PageIndex{4}\)
Determine\(I_D\) y\(V_{DS}\) para el circuito que se muestra en la Figura\(\PageIndex{14}\). Supongamos\(I_{DSS}\) = 12 mA y\(V_{GS(off)}\) = −4 V.
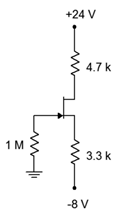
Figura\(\PageIndex{14}\): Esquema por ejemplo\(\PageIndex{4}\).
Usando el método gráfico, primero determine\(g_{m0} R_S\).
\[g_{m0} =− \frac{2 I_{DSS}}{V_{GS (off )}} \nonumber \]
\[g_{m0} = − \frac{2 \times 12 mA}{−4V} \nonumber \]
\[g_{m0} = 6mS \nonumber \]
Por lo tanto\(g_{m0} R_S\) = 6 mS\(\cdot\) 3.3 k\(\Omega\) = 19.8. El ratio de pantanos,\(k\), es\(V_{SS}/V_{GS(off)} = −8/−4 = 2\). Esto requiere la gráfica de la Figura\(\PageIndex{13a}\). Esta gráfica rinde aproximadamente 0.25 para la relación de corriente normalizada. Por lo tanto
\[I_D = 0.25 I_{DSS} \nonumber \]
\[I_D = 0.25 \times 12 mA \nonumber \]
\[I_D = 3mA \nonumber \]
Usando la ley de Ohm y KVL
\[V_D = V_{DD} − I_D R_D \nonumber \]
\[V_D = 24 V−3mA \times 4.7k\Omega \nonumber \]
\[V_D = 9.9 V \nonumber \]
\[V_S = V_{SS}+I_D R_S \nonumber \]
\[V_S =−8V+3mA \times 3.3 k\Omega \nonumber \]
\[V_S = 1.9V \nonumber \]
\[V_{DS} = V_D −V_S \nonumber \]
\[V_{DS} = 9.9 V −1.9V \nonumber \]
\[V_{DS} = 8 V \nonumber \]
Como comprobación cruzada, usando la ecuación\ ref {10.9} produce 3.028 mA para\(I_D\). La desviación se debe sin duda a la inexactitud en la lectura de la gráfica. En cualquier caso, utilizando este valor de corriente de drenaje encontramos\(V_S\) que es de 1.992 voltios, un poco más alto de lo calculado anteriormente. Esto indica que\(V_{GS}\) es −1.992 voltios (porque\(V_G \approx 0\) V). Si enchufamos este valor de\(V_{GS}\) en la Ecuación 10.2.1,\(I_D = 3.024\) mA; una excelente coincidencia con la desviación que se debe a errores de redondeo acumulados.
Para mostrar el aumento de la estabilidad del punto Q del sesgo combinado, repetiremos el problema anterior usando un JFET con un sesgo significativamente menor\(I_{DSS}\).
Ejemplo\(\PageIndex{5}\)
Determine\(I_D\) para el circuito que se muestra en la Figura\(\PageIndex{14}\). Supongamos\(I_{DSS}\) = 8 mA y\(V_{GS(off)}\) = −4 V.
Para esta versión usaremos Ecuación\ ref {10.9}. Primero determinar\(g_{m0} R_S\).
\[g_{m0} =− \frac{2 I_{DSS}}{V_{GS (off )}} \nonumber \]
\[g_{m0} =− \frac{2 \times 8mA}{−4 V} \nonumber \]
\[g_{m0} = 4 mS \nonumber \]
Por lo tanto\(g_{m0} R_S\) = 4 mS\(\cdot\) 3.3 k\(\Omega = 13.2\). El ratio de pantanos,\(k\), es\(V_{SS}/V_{GS(off)} = −8/−4 = 2\).
\[I_D =2 I_{DSS} \left( \frac{1+g_{m0} R_S (1+k) −\sqrt{1+2 g_{m0} R_S (1+k )}}{( g_{m0} R_S )^2} \right) \nonumber \]
\[I_D = 2 \times 8mA \left( \frac{1+13.2(1+2)−\sqrt{1+2 \times 13.2(1+2)}}{(13.2)^2} \right) \nonumber \]
\[I_D =2.906 mA \nonumber \]
Para el método gráfico, una estimación razonable para el normalizado\(I_D\) sería alrededor de 0.36, produciendo una corriente de drenaje de 2.88 mA. La estabilidad es evidente porque la corriente de drenaje ha bajado solo un poco por ciento a pesar de que\(I_{DSS}\) disminuyó en 33%.
La gráfica de la Figura\(\PageIndex{15}\) ilustra muy bien el aumento de la estabilidad del punto Q. Una vez más, trazamos dos curvas representativas del dispositivo en verde y azul. Como fue el caso del autosesgo, se puede trazar una línea de trama, cuya pendiente es igual al recíproco de\(R_S\). Sin embargo, esta línea argumental no pasa por el origen. En cambio, la intercepción\(x\) del eje es la tensión\(|V_{SS}|\). Así, la línea gráfica roja se desplaza a lo largo del\(V_{GS}\) eje.
Como puede verse en la gráfica, la variación en\(I_D\) se reduce (aunque a expensas de la variación en\(V_{GS}\)). Para valores grandes de\(V_{SS}\) con valores correspondientemente grandes de\(R_S\), la línea de trazado de sesgo se vuelve casi horizontal, lo que indica un punto Q muy estable. Con dos variables en juego, este sesgo demuestra ser muy flexible. También se puede realizar usando un divisor de voltaje positivo en la puerta y quitando\(V_{SS}\) (volviendo\(R_S\) a tierra).
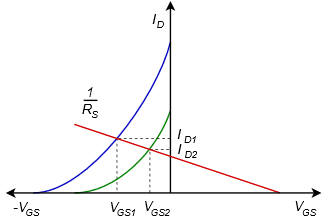
Figura\(\PageIndex{15}\): Variación para sesgo de combinación.
10.4.5: polarización de corriente constante
El sesgo más estable para los JFET se basa, curiosamente, en una fuente de corriente hecha con un BJT. Se llama polarización de corriente constante, otra etiqueta imaginativa más. Curiosamente, aunque esto mantendrá el punto Q muy estable, un fijo\(I_D\) no garantiza el valor más estable de ganancia de voltaje. De hecho, podría ser más fácil lograr ese objetivo usando el sesgo combinado. El prototipo de circuito de polarización de corriente constante se muestra en la Figura\(\PageIndex{16}\). Un BJT NPN se usa para un JFET de canal N y un PNP se usaría con un JFET de canal P, típicamente accionado desde arriba (es decir, circuito volteado de arriba a abajo).
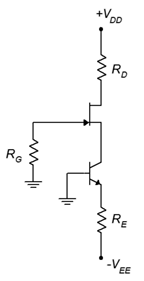
Figura\(\PageIndex{16}\): Prototipo de polarización de corriente constante.
Ignorando el JFET por un momento, el BJT se configura como en polarización de emisor de dos fuentes. En este caso la base está atada directamente a tierra, dejando el emisor a aproximadamente −0.7 VCC. El resto del\(V_{EE}\) suministro cae a través\(R_E\), estableciendo la corriente del emisor. Como el colector está conectado directamente al terminal fuente del JFET, esto significa que\(I_S \approx I_E\). La corriente fuente termina siendo igual de estable que la corriente del emisor, que ya hemos visto es muy estable. El único requisito es que no se\(I_E\) debe programar para que sea mayor que\(I_{DSS}\). Siendo esto cierto,\(I_D\) se establecerá un correspondiente\(V_{GS}\). Esto también establece\(V_S\) porque\(V_G \approx 0\) V. Por lo tanto, el terminal fuente será un pequeño voltaje positivo y esto es precisamente lo que necesita el BJT para garantizar que su unión colector-base sea polarizada en sentido inverso.
El cálculo de las corrientes y voltajes del circuito es sencillo y no implica el uso de auxiliares gráficos. El primer paso es examinar el bucle emisor del BJT y determinar\(I_E\). Una vez que se encuentra esto,\(I_S\) y\(I_D\) se conocen, y todos los potenciales de componentes restantes se pueden encontrar usando la ley de Ohm y KVL.
Esta técnica no implica el cálculo de\(V_{GS}\). De hecho, debido a que\(I_D\) es muy estable,\(V_{GS}\) mostrará la variación más amplia de todos los circuitos de polarización cuando se cambie el JFET. Si\(V_{GS}\) es necesario, se puede determinar mediante una pequeña manipulación algebraica en la Ecuación 10.2.1.
Ejemplo\(\PageIndex{6}\)
Detemine\(I_D\),\(V_{DS}\) y\(V_{GS}\) en el circuito de Figura\(\PageIndex{17}\). \(I_{DSS}\)= 15 mA y\(V_{GS(off)}\) = −3 V.
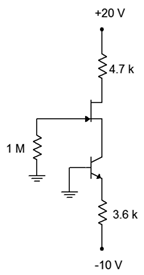
Figura\(\PageIndex{17}\): Esquema por ejemplo\(\PageIndex{6}\).
Empezamos por encontrar\(I_E\).
\[I_E = \frac{∣V_{EE}∣−0.7V}{R_E} \nonumber \]
\[I_E = \frac{10V −0.7V}{3.6k \Omega} \nonumber \]
\[I_E = 2.58mA \nonumber \]
\(I_E\)es lo mismo que\(I_S\) y\(I_D\), por lo tanto
\[V_D = V_{DD} −I_D R_D \nonumber \]
\[V_D = 20 V −2.58 mA \times 4.7 k\Omega \nonumber \]
\[V_D = 7.87V \nonumber \]
Para encontrar\(V_S\) notamos eso\(V_S = −V_{GS}\) y reorganizamos la Ecuación 10.2.1.
\[I_D = I_{DSS} \left( 1 − \frac{V_{GS}}{V_{GS (off )}} \right)^2 \nonumber \]
\[V_{GS} = V_{GS (off )} \left( 1 − \sqrt{\frac{I_D}{I_{DSS}}} \right) \nonumber \]
\[V_{GS} = −3 V \left(1 − \sqrt{\frac{2.58 mA}{15 mA}} \right) \nonumber \]
\[V_{GS} =−1.24 V \nonumber \]
Por lo tanto\(V_S = 1.24\) V y
\[V_{DS} = V_D −V_S \nonumber \]
\[V_{DS} = 7.87 V −1.24 V \nonumber \]
\[V_{DS} = 6.63 V \nonumber \]
Pasamos junto a una simulación por computadora de un circuito similar para validar nuestra metodología.
Simulación por Computadora
Un circuito de polarización de corriente constante se introduce en un simulador como se muestra en la Figura\(\PageIndex{18}\).
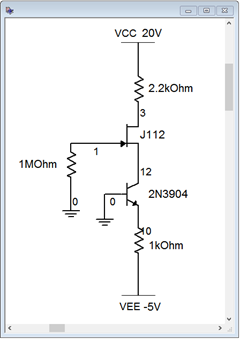
Figura\(\PageIndex{18}\): Circuito de polarización de corriente constante en simulador.
Una estimación superficial muestra que\(I_E\) y\(I_D\) debe estar alrededor de 4.3 mA. Además,\(V_D\) debe ser aproximadamente 20 V − 4.3 mA\(\cdot\) 2.2 k\(\Omega\), o aproximadamente 10.54 voltios. Los resultados de un análisis de punto de operación de CC se muestran en la Figura\(\PageIndex{19}\).
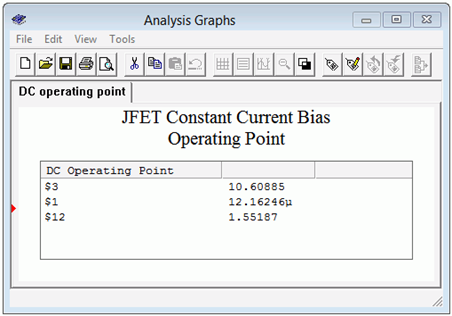
Figura\(\PageIndex{19}\): Resultados de simulación de punto de funcionamiento de CC de polarización de corriente constante.
El voltaje de drenaje (nodo 3) es poco más de 10.6 voltios, coincidiendo con nuestra estimación. También, tenga en cuenta el minúsculo voltaje de puerta (nodo 1) de 12\(\mu\) V que verifica nuestra suposición continua en estos circuitos que\(V_G \approx 0\) VCC. Finalmente, vemos un potencial modesto de aproximadamente 1.5 voltios en el terminal fuente (nodo 12). Esto muestra el correcto sesgo inverso de las uniones puerta-fuente y colector-base.
Finalmente, podemos examinar la variación del punto Q usando la Figura\(\PageIndex{20}\). Aquí, la línea de trazado es perfectamente horizontal y toda la variación del dispositivo se manifiesta en\(V_{GS}\).
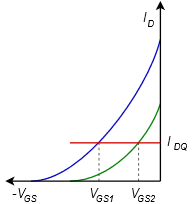
Figura\(\PageIndex{20}\): Variación para polarización de corriente constante.
Referencias
1 Podríamos agregar un tercer eje para\(k\) y trazar una superficie, y aunque podría ser bonita, una gráfica 3D como esta renderizada sobre una superficie 2D, como una página en un libro de texto, es de utilidad marginal.


