12.6: Biasing E-MOSFET
- Page ID
- 83374
Como el E-MOSFET opera sólo en el primer cuadrante, ninguno de los esquemas de polarización utilizados con los JFET funcionará con él. En primer lugar, cabe señalar que para aplicaciones de conmutación de señales grandes, la polarización no es un gran problema ya que simplemente necesitamos confirmar que hay suficiente señal de accionamiento para encender el dispositivo. Para amplificadores lineales podemos usar variaciones en la polarización de voltaje constante, como la polarización del divisor de voltaje o en la polarización de retroalimentación de drenaje.
12.6.1: Bias del divisor de voltaje
La polarización del divisor de voltaje es una reminiscencia del circuito divisor utilizado con los BJT. De hecho, el E-MOSFET de canal N requiere que su puerta sea más alta que su fuente, así como el NPN BJT requiere una tensión base mayor que su emisor. Las principales diferencias entre los dos son que la corriente de puerta de entrada del E-MOSFET es insignificante en comparación con la corriente base y que el voltaje puerta-fuente probablemente será más alto que la caída de 0.7 voltios vista a través de la unión base-emisor. Además, el voltaje puerta-fuente no se bloqueará a un voltaje específico sino que variará dependiendo del resto del circuito.
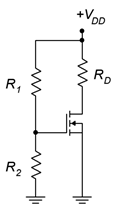
Figura\(\PageIndex{1}\): Polarización del divisor de voltaje para E-MOSFET.
El prototipo para la polarización del divisor de voltaje se muestra en la Figura\(\PageIndex{1}\). En general, la disposición es la misma que la polarización del divisor de voltaje utilizada con el DE-MOSFET. Las resistencias\(R_1\) y\(R_2\) configuran el divisor para establecer el voltaje de la puerta. Como el terminal fuente está atado directamente a tierra, esto significa que\(V_{GS} = V_G\). El potencial transversal\(R_2\) debe establecerse anteriormente\(V_{GS(th)}\) para un funcionamiento adecuado de acuerdo con la Ecuación 12.4.1. Conociendo el valor de\(V_G\), ya sea la ecuación característica o la gráfica de corriente de drenaje normalizada correspondiente se puede utilizar para determinar la corriente de drenaje. El único factor que falta es la constante del dispositivo,\(k\). Esto se puede calcular para cualquier dispositivo en particular basado en el\(I_{D(on)}\) par de\(V_{GS(on)}\) coordenadas especificado en la hoja de datos (o medido en laboratorio). Un ejemplo se muestra en la Figura\(\PageIndex{2}\).
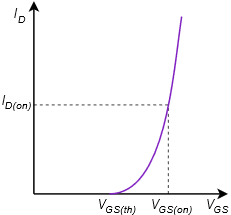
Figura\(\PageIndex{2}\): Par de coordenadas en la curva E-MOSFET.
La constante\(k\) se encuentra a través de un reordenamiento de la Ecuación 12.4.1:
\[k = \frac{I_{D(on )}}{(V_{GS (on )} −V_{GS (th )} )^2} \nonumber \]
Este valor se puede utilizar para otros puntos de polarización.
Ejemplo\(\PageIndex{1}\)
Para el circuito y la curva del dispositivo coincidente de la Figura\(\PageIndex{3}\), encontrar\(I_D\) y\(V_{DS}\).
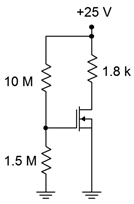
Figura\(\PageIndex{3a}\): Circuito por Ejemplo\(\PageIndex{1}\).
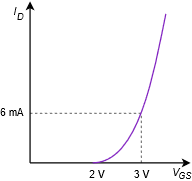
Figura\(\PageIndex{3b}\): Curva del dispositivo para Ejemplo\(\PageIndex{1}\).
Primero encuentra el valor de\(k\):
\[k = \frac{I_{D(on )}}{(V_{GS (on )}−V_{GS (th )} )^2} \nonumber \]
\[k = \frac{6 mA}{(3 V −2 V)^2} \nonumber \]
\[k = 6 mA/V^2 \nonumber \]
Ahora determine el voltaje de la puerta:
\[V_G = V_{DD} \frac{R_2}{R_1+R_2} \nonumber \]
\[V_G = 25 V \frac{1.5M \Omega}{10 M \Omega +1.5M \Omega} \nonumber \]
\[V_G = 3.26 V \nonumber \]
La fuente está puesta a tierra así\(V_{GS} = V_G\).
\[I_D = k (V_{GS} −V_{GS (th)} )^2 \nonumber \]
\[I_D = 6mA/V^2 (3.26 V −2 V)^2 \nonumber \]
\[I_D = 9.54 mA \nonumber \]
\[V_{DS} = V_{DD} −I_D R_D \nonumber \]
\[V_{DS} = 25V−9.54 mA \times 1.8 k \Omega \nonumber \]
\[V_{DS} = 7.83 V \nonumber \]
Para cerrar, observar que es posible desacoplar el divisor de voltaje utilizando el mismo método empleado con los BJT en la Figura 7.3.11. Resistencias de muy gran valor están disponibles en solo una variedad limitada de tamaños por lo que esta técnica tiene un beneficio agregado. Las resistencias divisoras pueden usar tamaños más convenientes porque\(R_1\) y no\(R_2\) establecerán la impedancia de entrada; será establecida por la resistencia de desacoplamiento.
12.6.2: Sesgo de retroalimentación de drenaje
El sesgo de retroalimentación de drenaje utiliza el punto de operación “encendido” mencionado anteriormente desde la curva característica. La idea es establecer una corriente de drenaje a través de una selección adecuada de la resistencia de drenaje y la fuente de alimentación. El prototipo del circuito de realimentación de drenaje se muestra en la Figura\(\PageIndex{4}\).
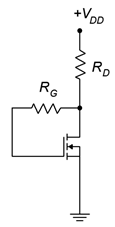
Figura\(\PageIndex{4}\): Prototipo de polarización de retroalimentación de drenaje
Este es un diseño relativamente simple usando pocos componentes. La clave para entender su funcionamiento es la suma KVL:
\[V_{DD} = V_{R_{D}} +V_{R_G} +V_{GS} \nonumber \]
\[V_{DD} = I_D R_D+I_G R_G+V_{GS} \nonumber \]
La corriente de la puerta es insignificante, lo que significa que
\[V_{DD} = I_D R_D+V_{GS} \nonumber \]
y también
\[V_{DS} = V_{GS} \nonumber \]
Por lo tanto,
\[V_{GS} = V_{DS} = V_{DD} −I_D R_D \label{12.7} \]
La ecuación\ ref {12.7} se puede utilizar como base para el diseño del circuito de polarización.
Ejemplo\(\PageIndex{2}\)
Utilizando el prototipo de la Figura\(\PageIndex{4}\), determinar valores para\(R_D\) y\(R_G\) tal que la corriente de drenaje sea de 8 mA. Supongamos\(V_{DD} = 20\) V,\(I_{D(on)} = 5\) mA en\(V_{GS(on) = 4}\) V y\(V_{GS(th)} = 2.5\) V.
Primero encuentra el valor de\(k\):
\[k = \frac{I_{D(on)}}{(V_{GS (on)} − V_{GS (th)} )^2} \nonumber \]
\[k = \frac{5mA}{(4 V −2.5 V)^2} \nonumber \]
\[k = 2.22mA/V^2 \nonumber \]
Ahora determine lo requerido\(V_{GS}\) para obtener 8 mA de corriente de drenaje reordenando la Ecuación 12.4.1.
\[I_D = k(V_{GS} −V_{GS (th)} )^2 \nonumber \]
\[V_{GS} = V_{GS (th)} + \sqrt{\frac{I_D}{k}} \nonumber \]
\[V_{GS} = 2.5V+ \sqrt{\frac{8mA}{2.22 mA/V^2}} \nonumber \]
\[V_{GS} = 4.4 V \nonumber \]
Y por último,
\[V_{GS} = V_{DS} = V_{DD} −I_D R_D \nonumber \]
\[R_D = \frac{V_{DD} − V_{GS}}{I_D} \nonumber \]
\[R_D = \frac{20 V −4.4 V}{8mA} \nonumber \]
\[R_D = 1.95 k \Omega \nonumber \]