14.2: Conceptos básicos de Clase D
- Page ID
- 83363
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)La clave para la alta eficiencia de la operación de clase D es operar solo los dispositivos de salida como interruptores. Es decir, se operan en los extremos extremos de la línea de carga, ya sea en corte o saturación. La única excepción a esta regla es cuando el dispositivo de salida está pasando de un estado a otro. Se pueden usar BJT o E-MOSFET, aunque por razones que examinaremos, los E-MOSFET tienden a ser preferidos en muchas aplicaciones y por lo tanto los usaremos aquí como regla general.
Para comprender la ventaja de potencia de la conmutación de clase D, considere el circuito de la Figura\(\PageIndex{1}\). Aquí tenemos un E-MOSFET siendo impulsado por una onda cuadrada en su terminal de puerta. La onda cuadrada va de cero a algún voltaje muy por encima\(V_{GS(th)}\), suficiente para encender completamente el MOSFET.
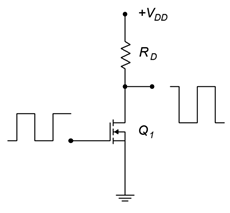
Figura\(\PageIndex{1}\): Un simple conmutador MOSFET.
En el desagüe aparece una onda cuadrada invertida que idealmente va de\(+V_{DD}\) abajo a cero voltios. Cuando el MOSFET está apagado, no fluye corriente de drenaje. Por lo tanto, la caída a través de la resistencia de drenaje\(R_{D}\),, es cero. En consecuencia, por KVL,\(V_{DS}\) debe igualar\(V_{DD}\). Cuando la señal de puerta se pone alta, enciende el MOSFET provocando una gran corriente. Idealmente, esta corriente es igual\(V_{DD}/R_D\) y\(V_{DS} = 0\) V. En realidad, el MOSFET presentará alguna resistencia\((r_{DS(on)})\) y esto esencialmente crea un divisor de voltaje entre el dispositivo y\(R_D\). Obviamente, si\(r_{DS(on)} \ll R_D\) entonces podemos aproximar el estado bajo como cero voltios.
En el caso ideal, el transistor no disipa energía. He aquí por qué: Cuando la puerta está baja, el dispositivo está apagado por lo que no fluye corriente. Aunque el voltaje del dispositivo es muy alto, el producto del voltaje y la corriente del dispositivo es cero. Cuando la puerta está alta, el transistor se enciende y conduce la corriente máxima, sin embargo, el voltaje a través del dispositivo es cero, y el producto resultante es cero una vez más. Por lo tanto, el dispositivo no disipa energía.
La realidad de la situación revela que parte de la energía es efectivamente desperdiciada por el dispositivo de salida. Hay dos principales culpables: voltaje de encendido distinto de cero (causado por ejemplo, por\(r_{DS(on)}\) ejemplo) y transiciones de estado que no son instantáneas (es decir, los tiempos de subida y caída de las formas de onda no son cero). Estos efectos se ilustran en la Figura\(\PageIndex{2}\).
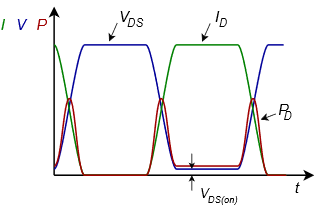
Figura\(\PageIndex{2}\): Pérdidas por conmutación.
Los tiempos de subida y caída son exagerados para mayor claridad al igual que la caída de voltaje a través del transistor. La curva verde representa la corriente del dispositivo mientras que la curva azul indica el voltaje del dispositivo. Tenga en cuenta que durante el estado encendido el voltaje del transistor no es cero, aunque es muy pequeño. El producto de estas dos curvas es la potencia disipada por el transistor y se muestra en rojo. En el estado apagado, no se disipa ninguna energía. En el estado encendido, una pequeña cantidad de energía se disipa debido al voltaje de encendido del dispositivo. Los picos de potencia también ocurren en las transiciones de estado ya que ni la corriente ni el voltaje están en cero.
El área bajo la curva roja representa la potencia total disipada por el transistor de salida. Para minimizar esta pérdida y maximizar la eficiencia, nos gustaría lo más baja\(r_{DS(on)}\) posible junto con velocidades de conmutación muy rápidas. Como los EMOSFET de potencia tienden a cambiar más rápido que sus contrapartes de BJT, esto presenta un argumento convincente para su uso. Además, los E-MOSFET de gran potencia pueden exhibir\(r_{DS(on)}\) valores de solo unos pocos miliohmios, lo que garantiza pérdidas de estado encendido relativamente pequeñas (en comparación con la potencia de carga) incluso con corrientes de drenaje de varias decenas de amperios.


