7.1: Línea de Transmisión de Alambre Paralelo
- Page ID
- 83660
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Una línea de transmisión de cable paralelo consiste en cables separados por un espaciador dieléctrico. La figura\(\PageIndex{1}\) muestra una implementación común, comúnmente conocida como “cable gemelo”. Los cables en la línea de conductores gemelos se mantienen en su lugar mediante un espaciador mecánico compuesto por el mismo material dieléctrico de baja pérdida que forma la camisa de cada cable. Muy poca de la energía total asociada a los campos eléctricos y magnéticos se encuentra dentro de este material, por lo que la camisa y el espaciador generalmente pueden descuidarse para fines de análisis y diseño eléctrico.

La línea de transmisión de cable paralelo se emplea a menudo en aplicaciones de radio de hasta aproximadamente\(100\) MHz como alternativa a la línea coaxial. La línea de cable paralelo tiene las ventajas de menor costo y menor pérdida que la línea coaxial en este rango de frecuencia. Sin embargo, la línea de cable paralelo carece de la propiedad de autoblindaje del cable coaxial; es decir, los campos electromagnéticos de la línea coaxial están aislados por el conductor externo, mientras que los de la línea de cable paralelo están expuestos y son propensos a la interacción con estructuras y dispositivos cercanos. Esto evita el uso de línea de alambre paralelo en muchas aplicaciones.
Otro discriminador entre la línea de cable paralelo y la línea coaxial es que la línea de cable paralelo es diferencial. 1 La geometría del conductor es simétrica y ninguno de los conductores es favorecido como dato de señal (“tierra”). Por lo tanto, la línea de cable paralelo se usa comúnmente en aplicaciones donde las fuentes de señal y/o las cargas también son diferenciales; ejemplos comunes son la antena dipolo y los amplificadores diferenciales. 2
La figura\(\PageIndex{2}\) muestra una sección transversal de línea de alambre paralelo.

Los parámetros relevantes incluyen el diámetro del alambre,\(d\); y el espaciamiento de centro a centro,\(D\).
La estructura de campo asociada es electromagnética transversal (TEM) y por lo tanto se describe completamente por una sola sección transversal a lo largo de la línea, como se muestra en la Figura\(\PageIndex{3}\).
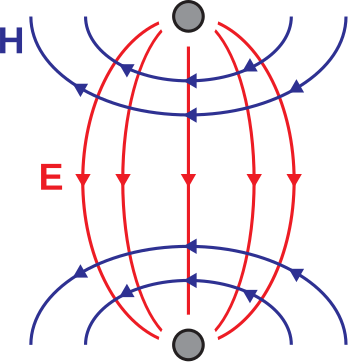
Las expresiones para estos campos existen, pero son complejas y no particularmente útiles excepto como medio para calcular otros parámetros de interés. Uno de estos parámetros es, por supuesto, la impedancia característica ya que este parámetro juega un papel importante en el análisis y diseño de sistemas que emplean líneas de transmisión. “La impedancia característica se puede determinar usando el modelo de línea de transmisión “" elemento agrupado "” usando la siguiente expresión:”
\[Z_0 = \sqrt{\frac{R'+j\omega L'}{G'+j\omega C'}} \nonumber \]
donde\(R'\),\(G'\)\(C'\), y\(L'\) son la resistencia, conductancia, capacitancia e inductancia por unidad de longitud, respectivamente. Este análisis se simplifica considerablemente al descuidar la pérdida; por lo tanto, supongamos las condiciones de “baja pérdida”\(R' \ll \omega L'\) y\(G' \ll \omega C'\). Luego encontramos:
\[Z_0 \approx \sqrt{\frac{L'}{C'}}~~~\mbox{(low loss)} \label{m0188_eZ0LL} \]
y el problema se reduce a determinar la inductancia y capacitancia de la línea de transmisión. Estos son
\[L' = \frac{\mu_0}{\pi}\ln\left[ \left(D/d\right) +\sqrt{\left(D/d\right)^2-1 } \right] \nonumber \]
\[C' = \frac{\pi\epsilon}{\ln\left[ \left(D/d\right) +\sqrt{\left(D/d\right)^2-1 } \right]} \nonumber \]
Debido a que la separación del cable\(D\) suele ser mucho mayor que el diámetro del cable\(d\),\(D/d\gg 1\) y así\(\sqrt{\left(D/d\right)^2-1} \approx D/d\). Esto lleva a las expresiones simplificadas
\[L' \approx \frac{\mu_0}{\pi}\ln\left( 2D/d \right) ~~~ (D \gg d) \nonumber \]
\[C' \approx \frac{\pi\epsilon}{\ln\left( 2D/d \right)} ~~~ (D \gg d) \nonumber \]
Ahora volviendo a la Ecuación\ ref {M0188_EZ0LL}:
\[Z_0 \approx \frac{1}{\pi}\sqrt{\frac{\mu_0}{\epsilon}}\ln\left( 2D/d \right) \nonumber \]
Señalando que\(\epsilon=\epsilon_r\epsilon_0\) y\(\sqrt{\mu_0/\epsilon_0}\triangleq\eta_0\), obtenemos
\[\boxed{ Z_0 \approx \frac{1}{\pi}\frac{\eta_0}{\sqrt{\epsilon_r}}\ln\left( 2D/d \right) } \label{m0188_eZ0PWL} \]
La impedancia característica de la línea de cable paralelo, asumiendo condiciones de baja pérdida y espaciado de cables mucho mayor que el diámetro del cable, viene dada por la Ecuación\ ref {M0188_EZ0PWL}.
Observe que la impedancia característica de la línea de cable paralelo aumenta con el aumento\(D/d\). Dado que esta relación es grande, la impedancia característica de la línea de cable paralelo tiende a ser grande en relación con los valores comunes de otros tipos de línea de transmisión TEM, como la línea coaxial y la línea de microcinta. A continuación se muestra un ejemplo.
Una forma común de línea de transmisión de cable paralelo es el\(300~\Omega\) cable doble. Aunque las implementaciones varían, el diámetro del alambre suele ser de aproximadamente 1 mm y la separación del cable suele ser de aproximadamente 6 mm. La permitividad relativa del medio\(\epsilon_r\approx 1\) para los fines de calcular los parámetros de la línea de transmisión, ya que la camisa y el espaciador solo tienen un pequeño efecto en los campos. Para estos valores, la Ecuación\ ref {M0188_EZ0PWL} da\(Z_0\approx 298~\Omega\), como se esperaba.
Bajo el supuesto de que el material de la camisa de alambre/espaciador tiene un efecto insignificante sobre los campos electromagnéticos, y que la línea está suspendida en el aire de manera que\(\epsilon_r\approx 1\), la velocidad de fase\(v_p\) para una línea de cable paralela es aproximadamente la de cualquier onda electromagnética en el espacio libre; es decir,\(c\). En la práctica de doble plomo, el efecto de una camisa plástica/material espaciador es reducir la velocidad de fase en un poco por ciento hasta aproximadamente 20%, dependiendo de los materiales y detalles de construcción. Así que en la práctica\(v_p\approx 0.8c\)\(0.9c\) para la línea de doble ventaja.
Lectura adicional:
- “Twin-lead” en Wikipedia.
- “Señalización diferencial” en Wikipedia.
- Sec. 8.7 (“Circuitos Diferenciales”) en S.W. Ellingson, Ingeniería de Sistemas de Radio, Cambridge Univ. Prensa, 2016.
- Las referencias en “Lectura adicional” al final de esta sección pueden ser útiles si no está familiarizado con este concepto. ↩
- Esto contrasta con la línea “de un solo extremo” como la línea coaxial, que tiene conductores de diferentes secciones transversales y el conductor externo se ve favorecido como el dato. ↩


