9.4: Radiación de un dipolo hertziano
- Page ID
- 83730
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En la sección 9.1 se presentó una derivación informal del campo electromagnético irradiado por un dipolo hertziano representado por un momento de corriente de longitud cero. En esta sección, se proporciona una derivación rigurosa utilizando el concepto de potencial de vector magnético discutido en las Secciones 9.2 y 9.3. Se recomienda revisar esas secciones antes de abordar esta sección.
Un dipolo hertziano se define comúnmente como un filamento recto de corriente eléctrico corto e infinitesimalmente delgado, en el que la densidad de la corriente es uniforme a lo largo de su longitud. El dipolo hertziano se usa comúnmente como un “bloque de construcción” para construir distribuciones de corriente físicamente-realizables como exhibidas por dispositivos tales como antenas de alambre. El método consiste en modelar estas distribuciones relativamente complejas de corriente como la suma de dipolos hertzianos, lo que reduce el problema al de sumar las contribuciones de los dipolos hertzianos individuales, teniendo cada dipolo hertziano la posición, magnitud y fase apropiadas (es decir, diferentes).
Para facilitar el uso del dipolo hertziano como un bloque de construcción adecuado para construir distribuciones de corriente materialmente realizables, elegimos representar el dipolo hertziano usando una distribución de corriente esencialmente equivalente que es matemáticamente más versátil. Esta descripción del dipolo hertziano reemplaza la noción de corriente constante sobre longitud finita con la noción de un momento actual ubicado en un solo punto. Esto se muestra en la Figura\(\PageIndex{1}\),
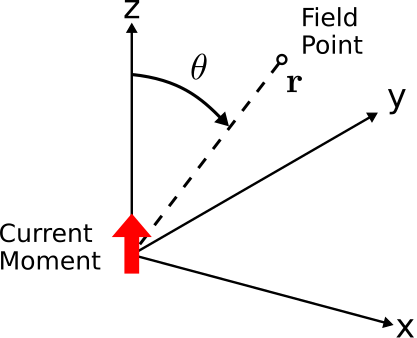
y está dada por:
\[\Delta\widetilde{\bf J}({\bf r}) = \hat{\bf l}~\widetilde{I}~\Delta l~\delta({\bf r}) \nonumber \]
donde el producto\(\widetilde{I}\Delta l\) (unidades base SI de A\(\cdot\) m) es el momento actual,\(\hat{\bf l}\) es la dirección del flujo de corriente y\(\delta({\bf r})\) es la función de muestreo volumétrico definida de la siguiente manera:
\ begin {align} ~ &\ delta ({\ bf r})\ triangleq 0~~~\ mbox {para} ~~~ {\ bf r}\ neq 0; ~~~\ mbox {y}\ label {m0197_Edelta1}\\ ~ &\ int_ {\ mathcal {V}}\ delta ({\ bf r}) ~dv\ triangleq leq 1\ etiqueta {M0197_Edelta2}\ end {align}
donde\(\mathcal{V}\) está cualquier volumen que incluya el origen (\({\bf r}=0\)). En esta descripción, el dipolo hertziano se localiza en el origen.
La solución para el potencial de vector magnético debido a un dipolo Hertziano\(\hat{\bf z}\) dirigido localizado en el origen se presentó en la Sección 9.3. En el escenario actual, es:
\[\widetilde{\bf A}({\bf r}) = \hat{\bf z}~\mu~\widetilde{I}~\Delta l~\frac{e^{-\gamma r} }{4\pi r} \nonumber \]
donde la constante de propagación\(\gamma=\alpha+j\beta\) como de costumbre. Asumiendo medios sin pérdidas (\(\alpha=0\)), tenemos
\[\widetilde{\bf A}({\bf r}) = \hat{\bf z}~\mu~\widetilde{I}~\Delta l~\frac{e^{-j\beta r} }{4\pi r} \nonumber \]
Obtenemos la intensidad del campo magnético utilizando la definición de potencial de vector magnético:
\ begin {align}\ Widetilde {\ bf H} &\ triangleq (1/\ mu)\ nabla\ veces\ Widetilde {\ bf A}\\ &=\ frac {\ Widetilde {I} ~\ Delta l} {4\ pi} ~\ nabla\ veces\ hat {\ bf z} ~\ frac {e^ {-j\ r beta}} {}\ etiqueta {m0197_h1}\ end {align}
Para proceder, es útil\(\hat{\bf z}\) convertir en el sistema de coordenadas esféricas. Para ello, encontramos que el componente de\(\hat{\bf z}\) eso es paralelo a\(\hat{\bf r}\),\(\hat{\bf \theta}\), y\(\hat{\bf \phi}\); y luego sumamos los resultados:
\ begin {align}\ hat {\ bf z} &=\ hat {\ bf r}\ left (\ hat {\ bf r}\ cdot\ hat {\ bf z}\ right) +\ hat {\ bf\ theta}\ left (\ hat {\ bf\ theta}\ cdot\ hat {\ bf z}\ right) +\ hat {\ bf\ phi}\ left (\ hat {\ bf\ phi}\ cdot\ sombrero {\ bf z}\ derecho)\\ &=\ sombrero {\ bf r}\ cos\ theta -\ sombrero {\ bf\ theta}\ sin\ theta +0\ end {align}
La ecuación\ ref {M0197_H1} requiere el cálculo de la siguiente cantidad:
\ begin {align}\ nabla\ times\ hat {\ bf z}\ frac {e^ {-j\ beta r}} {r} &=\ nabla\ veces\ left [~~~\ hat {\ bf r}\ left (\ cos\ theta\ right)\ frac {e^ {-j\ beta r}} {r}\ derecha. \ nonumber\\ & ~~~~~~~~~~~~~~~~~~~\ izquierda. -\ hat {\ bf\ theta}\ izquierda (\ sin\ theta\ derecha)\ frac {e^ {-j\ beta r}} {r}\ derecha]\ etiqueta {m0197_e2}\ end {align}
En este punto, es conveniente hacer las siguientes definiciones:
\ begin {align} C_r &\ triangleq\ izquierda (\ cos\ theta\ derecha)\ frac {e^ {-j\ beta r}} {r}\\ C_ {\ theta} &\ triangleq -\ izquierda (\ sin\ theta\ derecha)\ frac {e^ {-j\ beta r}} {r}\ end {align}
Estas definiciones permiten que la ecuación\ ref {m0197_e2} se escriba de manera compacta de la siguiente manera:
\[\nabla\times \hat{\bf z}\frac{e^{-j\beta r}}{r} = \nabla\times\left[ ~\hat{\bf r}C_r + \hat{\bf \theta}C_{\theta} \right] \label{m0197_e1} \]
El lado derecho de la Ecuación\ ref {m0197_e1} se evalúa usando la Ecuación 12.2.9 (Apéndice 12.3.2). Aunque la expresión completa consta de 6 términos, sólo 2 términos son distintos de cero. 1 Esto deja:
\ begin {align}\ nabla\ times\ hat {\ bf z}\ frac {e^ {-j\ beta r}} {r} &=\ hat {\ bf\ phi}\ frac {1} {r}\ izquierda [\ frac {\ parcial} {\ parcial}\ izquierda (r C_ {\ theta}\ derecha) -\ frac {\ parcial} {\ parcial\ theta} C_r\ derecha]\\ &=\ sombrero {\ bf\ phi}\ izquierda (\ sin\ theta\ derecha)\ frac {e^ {-j\ beta r}} {r}\ izquierda (j\ beta +\ frac {1} {r}\ derecha)\ fin {alinear}
Sustituyendo este resultado en la Ecuación\ ref {M0197_H1}, obtenemos:
\[\widetilde{\bf H} = \hat{\bf \phi} \frac{\widetilde{I}~\Delta l}{4\pi}~\left(\sin\theta\right) \frac{e^{-j\beta r}}{r} \left( j\beta + \frac{1}{r} \right) \label{m0197_H2} \]
Limitemos aún más nuestro alcance al campo lejos de la antena. Específicamente, supongamos\(r\gg\lambda\). Ahora usamos la relación\(\beta=2\pi/\lambda\) y determinamos lo siguiente:
\ begin {align} j\ beta +\ frac {1} {r} &= j\ frac {2\ pi} {\ lambda} +\ frac {1} {r}\\ &\ approx j\ frac {2\ pi} {\ lambda} =j\ beta\ end {align}
La ecuación\ ref {M0197_h2} se convierte en:
\[\boxed{ \widetilde{\bf H} \approx \hat{\bf \phi} j \frac{\widetilde{I}\cdot\beta \Delta l}{4\pi}~\left(\sin\theta\right) \frac{e^{-j\beta r}}{r} } \label{m0197_H4} \]
donde se mantiene la aproximación para medios de baja pérdida y\(r\gg\lambda\). Esta expresión se conoce como aproximación de campo lejano, ya que es válida únicamente para distancias “lejanas” (relativas a una longitud de onda) desde la fuente.
Ahora tomemos un momento para interpretar este resultado:
- Observe que el factor\(\beta \Delta l\) tiene unidades de radianes; es decir, es longitud eléctrica. Esto nos dice que la magnitud del campo radiado depende de la longitud eléctrica del momento actual.
- El factor\(e^{-j\beta r}/r\) indica que se trata de una onda esférica; es decir, las superficies de fase constante corresponden a esferas concéntricas centradas en la fuente, y la magnitud es inversamente proporcional a la distancia.
- La dirección del vector del campo magnético es siempre\(\hat{\bf \phi}\), que es precisamente lo que esperamos; por ejemplo, utilizando la ley Biot-Savart.
- Por último, anotar el factor\(\sin\theta\). Esto indica que la magnitud del campo es cero a lo largo de la dirección en la que fluye la corriente de origen, y es un máximo en el plano perpendicular a esta dirección.
Ahora determinemos el campo eléctrico irradiado por el dipolo hertziano. El método directo es emplear la ley de Ampere. Es decir,
\[\widetilde{\bf E} = \frac{1}{j\omega\epsilon} \nabla \times \widetilde{\bf H} \nonumber \]
donde\(\widetilde{\bf H}\) viene dada por la Ecuación\ ref {M0197_H4}. En puntos de campo alejados del dipolo, el radio de curvatura de los frentes de fase esféricos es muy grande y por lo tanto parece ser localmente plano. Es decir, desde la perspectiva de un observador alejado del dipolo, la ola que llega parece ser una onda plana. En este caso, podemos emplear las relaciones de onda plana. La relación apropiada en este caso es:
\[\widetilde{\bf E} = -\eta \hat{\bf r} \times \widetilde{\bf H} \nonumber \]
donde\(\eta\) esta la impedancia de onda. Entonces encontramos:
\[\boxed{ \widetilde{\bf E} \approx \hat{\bf \theta} j\eta \frac{\widetilde{I}\cdot\beta \Delta l}{4\pi}~\left(\sin\theta\right) \frac{e^{-j\beta r}}{r} } \label{m0197_eE} \]
Resumiendo:
Los campos eléctricos y magnéticos alejados (es decir,\(\gg\lambda\)) de un dipolo Hertziano\(\hat{\bf z}\) -dirigido que tiene corriente constante\(\widetilde{I}\) sobre longitud\(\Delta l\), ubicados en el origen, están dados por las Ecuaciones\ ref {M0197_EE} y\ ref {M0197_H4}, respectivamente.
Lectura adicional:
- “Antena dipolo” (sección titulada “Dipolo Hertziano”) en Wikipedia.
- Específicamente, dos términos son cero porque no hay\(\hat{\bf \phi}\) componente en el argumento de la función curl; y otros dos términos son cero porque el argumento de la función curl es independiente de\(\phi\), por lo que las derivadas parciales con respecto a\(\phi\) son cero. ↩


