7.2: Redes de dos puertos

En los circuitos de microondas generalmente es difícil hacer esto. Recordemos que con las líneas de transmisión no es posible establecer un punto de tierra común. Sin embargo, con las líneas de transmisión se vio que por cada corriente de señal hay una corriente de retorno de señal. Así, a frecuencias de radio, y para circuitos que se distribuyen, se utilizan puertos, como se muestra en la Figura\(\PageIndex{1}\) (a), que definen los voltajes y corrientes para una red de dos puertos, o solo de dos puertos. \(^{1}\)La red en la Figura\(\PageIndex{1}\) (a) tiene cuatro terminales y dos puertos. Un voltaje de puerto se define como la diferencia de voltaje entre un par de terminales con uno de los terminales en el par convirtiéndose en el terminal de referencia. La corriente que ingresa a la red en el terminal superior del Puerto 1 es\(I_{1}\) y hay una corriente igual saliendo del terminal de referencia. Esta disposición claramente tiene sentido cuando las líneas de transmisión están conectadas a los Puertos 1 y 2, como en la Figura\(\PageIndex{1}\) (b). Con las líneas de transmisión en los puertos 1 y 2 habrá voltajes de onda viajera, y en los puertos los componentes de onda viajera se suman para dar el voltaje total del puerto. Al tratar con circuitos no distribuidos es preferible utilizar los voltajes y corrientes totales del puerto\(I_{2}\),\(V_{1},\: I_{1},\: V_{2},\) y, mostrados en la Figura\(\PageIndex{1}\) (a). Sin embargo, con elementos distribuidos es preferible tratar tensiones y corrientes de marcha\(V_{1}^{+},\:V_{1}^{-},\:V_{2}^{+}\), y\(V_{2}^{-}\), mostrado en la Figura\(\PageIndex{1}\) (b). El diseño de RF y microondas requiere necesariamente cambiar entre las dos formas.

7.2.1 Reciprocidad, simetría, pasividad y linealidad

Reciprocidad, simetría, pasividad y linealidad son propiedades fundamentales de las redes. Una red es lineal si la respuesta depende linealmente del nivel de accionamiento, y también se aplica la superposición. Entonces, si los dos puertos mostrados en la Figura\(\PageIndex{1}\) (a) son lineales, las corrientes\(I_{1}\) y\(I_{2}\) son funciones lineales de\(V_{1}\) y\(V_{2}\). Un ejemplo de una red lineal sería aquella con resistencias y capacitores. Una red con diodo sería no lineal. Una red pasiva no tiene fuentes internas de alimentación y una simétrica de dos puertos tiene las mismas características en cada uno de los puertos. Un ejemplo de una red simétrica es una línea de transmisión con una sección transversal uniforme.

Un recíproco de dos puertos tiene una respuesta en el Puerto 2 de una excitación en el Puerto 1 que es la misma que la respuesta en el Puerto 1 a la misma excitación en el Puerto 2. Como ejemplo, considere los dos puertos en la Figura\(\PageIndex{1}\) (a) con\(V_{2} = 0\). Si la red es recíproca, entonces la relación\(I_{2}/V_{1}\) con\(V_{2} = 0\) será la misma que la relación\(I_{1}/V_{2}\) con\(V_{1} = 0\). Las redes con resistencias, capacitores y líneas de transmisión son recíprocas. Un amplificador de transistor no es recíproco ya que la ganancia está en una dirección.

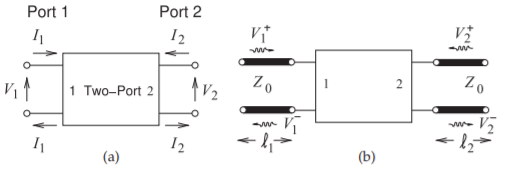
Figura\(\PageIndex{1}\): Una red de dos puertos: (a) voltajes de puerto; y (b) con líneas de transmisión en los puertos.

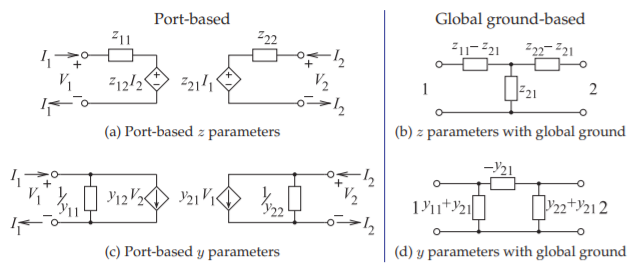
Figura\(\PageIndex{2}\): Los circuitos equivalentes a\(z\) - y\(y\) -parámetros para representaciones terrestres globales y basadas en puertos. Las inmitancias se muestran como impedancias.

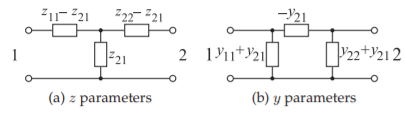
Figura\(\PageIndex{3}\): Equivalencia de circuito de los\(y\) parámetros\(z\) y para una red recíproca (en (b) los elementos son admitancias).

7.2.2 Parámetros basados en voltaje y corriente totales

Aquí se describirán los parámetros de impedancia (\(z\)\(y\)), admitancia () e híbrido (\(h\)) basados en puertos. Estos son similares a los\(h\) parámetros más convencionales\(z,\: y,\) y definidos con respecto a un terreno común o global. Las representaciones de circuitos contrastantes de los parámetros se muestran en la Figura\(\PageIndex{2}\).

Parámetros de Impedancia

Con referencia a\(\PageIndex{1}\) la Figura, los parámetros de impedancia basados en puertos, o\(z\) parámetros, se definen como

\[\label{eq:1}V_{1}=z_{11}I_{1}+z_{12}I_{2} \]

\[\label{eq:2}V_{2}=z_{21}I_{1}+z_{22}I_{2} \]

o en forma de matriz como

\[\label{eq:3}\mathbf{V}=\mathbf{ZI} \]

El subíndice doble en un parámetro se ordena de manera que el primero se refiere a la salida y el segundo se refiere a la entrada, así\(z_{ij}\) relaciona la salida de voltaje en Port\(i\) con la entrada de corriente en Port\(j\). Si la red es recíproca, entonces\(z_{12} = z_{21}\), pero este tipo simple de relación no se aplica a todos los parámetros de la red. La equivalencia recíproca del circuito de los\(z\) parámetros se muestra en la Figura\(\PageIndex{3}\) (a).

Ejemplo\(\PageIndex{1}\): Thevenin equivalent of a source with a two-port

¿Cuál es el circuito equivalente Thevenin de la red de dos puertos con terminación de origen a la derecha?

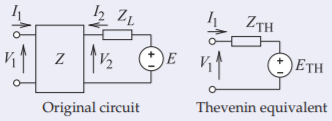
Figura\(\PageIndex{4}\)

Solución

Del circuito original

\[\label{eq:4}V_{1}=Z_{11}I_{1}+Z_{12}I_{2} \]

\[\label{eq:5}V_{2}=Z_{21}I_{1}+Z_{22}I_{2} \]

\[\label{eq:6}V_{2}=E-I_{2}Z_{L} \]

Sustitución de la ecuación\(\eqref{eq:6}\) en la ecuación\(\eqref{eq:5}\)

\[\label{eq:7}E=Z_{21}I_{1}+(Z_{22}+Z_{L})I_{2} \]

Multiplicando Ecuación\(\eqref{eq:4}\) por\((Z_{22} + Z_{L})\) y

Ecuación\(\eqref{eq:7}\) por\(Z_{12}\)

\[\label{eq:8}(Z_{22}+Z_{L})V_{1}=(Z_{22}+Z_{L})Z_{11}I_{1}+(Z_{22}+Z_{L})Z_{12}I_{2} \]

\[\label{eq:9}Z_{12}E=Z_{12}Z_{21}I_{1}+Z_{12}(Z_{22}+Z_{L})I_{2} \]

Restar la ecuación\(\eqref{eq:9}\) de la ecuación\(\eqref{eq:8}\)

\[(Z_{22} + Z_{L})V_{1} − Z_{12}E = [(Z_{22} + Z_{L})Z_{11}−]I_{1}\nonumber \]

\[\label{eq:10}V_{1}=\frac{Z_{12}E}{Z_{22}+Z_{L}}+\left(Z_{11}-\frac{Z_{12}Z_{21}}{Z_{22}+Z_{L}}\right)I_{1} \]

Para el circuito equivalente Thevenin\(V_{1} = E_{TH} + I_{1}Z_{TH}\) y así

\[\label{eq:11}Z_{TH}=\left(Z_{11}-\frac{Z_{12}Z_{21}}{Z_{22}+Z_{L}}\right)\quad\text{and}\quad E_{TH}=\frac{Z_{12}E}{Z_{22}+Z_{L}} \]

Parámetros de admisión

Los parámetros de admitancia basados en puertos, o\(y\) parámetros, se definen como

\[\label{eq:12}I_{1}=y_{11}V_{1}+y_{12}V_{2} \]

\[\label{eq:13}I_{2}=y_{21}V_{1}+y_{22}V_{2} \]

o en forma de matriz como

\[\label{eq:14}\mathbf{I}=\mathbf{YV} \]

Ahora, para la reciprocidad,\(y_{12} = y_{21}\) y la equivalencia de circuito de los\(y\) parámetros se muestra en la Figura\(\PageIndex{3}\) (b).

Notas al pie

[1] Incluso cuando el término “dos puertos” se usa por sí solo, se usa el guión, ya que se refiere a una red de dos puertos.