7.3: Parámetros de dispersión
- Page ID
- 81662
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)La medición directa de los\(y\) parámetros\(z\) y requiere que los puertos se terminen en circuitos cortos o abiertos. Para los circuitos activos esto podría resultar en un comportamiento no deseado, incluyendo oscilación o destrucción. Además, en RF es difícil realizar un buen abierto o corto. Dado que los circuitos de RF están diseñados con mucha atención a las condiciones de transferencia de potencia máxima, se prefieren las terminaciones resistivas, ya que estas están más cerca de las condiciones de operación reales. Por lo tanto, el efecto de los errores de medición tendrá menor impacto. Esta es la forma en que se miden los parámetros de dispersión.
La discusión de los parámetros de dispersión,\(S\) parámetros \(^{1}\), comienza considerando el coeficiente de reflexión, que es el\(S\) parámetro de una red de un puerto.
7.3.1 Coeficiente de Reflexión
El coeficiente de reflexión\(\Gamma\),, de una carga se\(\Gamma_{L}\) puede determinar midiendo por separado los voltajes de avance y retroceso en una línea de transmisión terminada por la carga:
\[\label{eq:1}\Gamma (x)=\frac{V^{-}(x)}{V^{+}(x)} \]
Imagínese entre la fuente y la carga que hay una línea de impedancia característica\(Z_{0}\) y con longitud infinitesimal, luego\(\Gamma\) a la carga se relaciona con la impedancia\(Z_{L}\) por
\[\label{eq:2}\Gamma (0)=\frac{Z_{L}-Z_{0}}{Z_{L}+Z_{0}} \]
donde\(Z_{0}\) está la impedancia característica de la línea de transmisión de conexión. Esto también se puede escribir como
\[\label{eq:3}\Gamma (0)=\frac{Y_{0}-Y_{L}}{Y_{0}+Y_{L}} \]
dónde\(Y_{0} = 1/Z_{0}\) y\(Y_{L} = 1/Z_{L}\). Más completamente,\(\Gamma\) como se definió anteriormente se llama el coeficiente de reflexión de voltaje a veces denotado\(\Gamma^{V}\).
Recordemos que el coeficiente de reflexión actual\(\Gamma^{I} = −\Gamma^{V}\).
7.3.2\(S\) Parámetros de dos puertos
Los\(S\) parámetros de dos puertos se definen en términos de ondas viajeras en líneas de transmisión con impedancia característica real\(Z_{0}\) conectada a cada uno de los puertos de una red, ver Figura 7.2.1 (b):
\[\label{eq:4}V_{1}^{-}=S_{11}V_{1}^{+}+S_{12}V_{2}^{+} \]
\[\label{eq:5}V_{2}^{-}=S_{21}V_{1}^{+}+S_{22}V_{2}^{+} \]
donde\(S_{ij}\) están los\(S\) parámetros individuales. En forma de matriz
\[\label{eq:6}\left[\begin{array}{l}{V_{1}^{-}}\\{V_{2}^{-}}\end{array}\right]=\left[\begin{array}{ll}{S_{11}}&{S_{12}}\\{S_{21}}&{S_{22}}\end{array}\right] \left[\begin{array}{l}{V_{1}^{+}}\\{V_{2}^{+}}\end{array}\right] =\mathbf{S}\left[\begin{array}{l}{V_{1}^{+}}\\{V_{2}^{+}}\end{array}\right] \]
Los\(S\) parámetros individuales se determinan midiendo las olas que viajan hacia adelante y hacia atrás con cargas\(Z_{0}\) en los puertos. Como la carga\(Z_{0}\) es no puede reflejar el poder y así\(V_{2}^{+}= 0\), entonces
\[\label{eq:7}S_{11}=\left. \frac{V_{1}^{-}}{V_{1}^{+}}\right| _{V_{2}^{+}=0} \]
Los parámetros restantes se determinan de manera similar y así S22 se encuentra como
\[\label{eq:8}S_{22}=\left. \frac{V_{2}^{-}}{V_{2}^{+}}\right| _{V_{1}^{+}=0} \]
y el parámetro de transmisión como
\[\label{eq:9}S_{21}=\left. \frac{V_{2}^{-}}{V_{1}^{+}}\right| _{V_{2}^{+}=0} \]
| \(S\) | En términos de\(S\) | |
|---|---|---|
| \(z\) | \ (S\) ">\(Z_{11}'=z_{11}Z_{0}\quad Z_{12}'=z_{12}Z_{0}\) | \ (S\) ">\(Z_{21}'=z_{21}Z_{0}\quad Z_{22}'=z_{22}Z_{0}\) |
| \ (S\) ">\(\begin{aligned} \delta_{z}&= (1+z_{11})(1+z_{22})-z_{12}z_{21} \\ S_{11}&=[(z_{11}-1)(z_{22}+1)-z_{12}z_{21}]/\delta_{z} \\ S_{12}&=2z_{12}/\delta_{z} \\ S_{21}&=2z_{21}/\delta_{z} \\ S_{22}&=[(z_{11}+1)(z_{22}-1)-z_{12}z_{21}]/\delta_{z}\end{aligned}\) | \ (S\) ">\(\begin{aligned}\delta_{S}&=(1-S_{11})(1-S_{22})-S_{12}S_{21} \\ z_{11}&=[(1+S_{11})(1-S_{22})+S_{12}S_{21}]/\delta_{S} \\ z_{12}&=2S_{12}/\delta_{S} \\ z_{21}&=2S_{21}/\delta_{S} \\ z_{22}&=[(1-S_{11})(1+S_{22})+S_{12}S_{21}]/\delta_{S}\end{aligned}\) | |
| \(y\) | \ (S\) ">\(Y_{11}'=y_{11}/Z_{0}\quad Y_{12}'=y_{12}/Z_{0}\) | \ (S\) ">\(Y_{21}'=y_{21}/Z_{0}\quad Y_{22}'=y_{22}/Z_{0}\) |
| \ (S\) ">\(\begin{aligned}\delta_{y}&=(1+y_{11})(1+y_{22})-y_{12}y_{21} \\ S_{11}&=[(1-y_{11})(1+y_{22})+y_{12}y_{21}]/\delta_{y} \\ S_{12}&=-2y_{12}/\delta_{y} \\ S_{21}&=-2y_{21}/\delta_{y} \\ S_{22} &=[(1+y_{11})(1-y_{22})+y_{12}y_{21}]/\delta_{y}\end{aligned}\) | \ (S\) ">\(\begin{aligned}\delta_{S}&=(1+S_{11})(1+S_{22})-S_{12}S_{21}\\ y_{11}&=[(1-S_{11})(1+S_{22})+S_{12}S_{21}]/\delta_{S} \\ y_{12}&=-2S_{12}/\delta_{S} \\ y_{21}&=-2S_{21}/\delta_{S} \\ y_{22}&=[(1+S_{11})(1-S_{22})+S_{12}S_{21}]/\delta_{S}\end{aligned}\) |
Tabla\(\PageIndex{1}\): Tabla de conversión de\(S\) parámetros de dos puertos. Los\(y\) parámetros\(z\), y se normalizan a\(Z_{0}\). \(Z′\)y\(Y′\) son los parámetros reales.
En la dirección inversa,
\[\label{eq:10}S_{12}=\left. \frac{V_{1}^{-}}{V_{2}^{+}}\right| _{V_{1}^{+}=0} \]
En lo anterior\(Z_{0}\) se conoce como la impedancia de normalización o equivalentemente la impedancia de referencia. En algunas circunstancias\(Z_{\text{REF}}\) se utiliza para denotar impedancia de referencia para evitar posibles confusiones con una impedancia de línea de transmisión que no es la misma que la impedancia de referencia. Los\(S\) parámetros aquí también se denominan\(S\) parámetros normalizados, y los\(S\) parámetros se normalizan a la misma impedancia de referencia real en cada puerto.
Las relaciones entre los parámetros de dos puertos y los\(S\) parámetros de red comunes se dan en la Tabla\(\PageIndex{1}\). Es interesante señalar eso\(S_{21}/S_{12} = z_{21}/z_{12} = y_{21}/y_{12}\). Es decir, la relación de los parámetros directo a inverso (al menos para\(S,\: z,\) y\(y\) parámetros) es la misma y esta relación es una para un dispositivo recíproco. Un\(S\) parámetro es una relación de voltaje, por lo que cuando se expresa en decibelios\(S_{ij}|_{\text{ dB}} = 20\log (S_{ij})\).
Una red recíproca tiene\(S_{12} = S_{21}\). Si la potencia de la unidad fluye hacia un puerto de dos, una fracción\(|S_{11}|^{2}\),, se refleja y otra fracción,\(|S_{21}|^{2}\), se transmite a través de la red.
Ejemplo\(\PageIndex{1}\): Two-Port \(S\) Parameters
¿Cuáles son los\(S\) parámetros de un\(30\text{ dB}\) atenuador?
Solución
Se muestra un atenuador con una impedancia del sistema de\(Z_{0}\). Un atenuador ideal no tiene reflexión en cada uno de los dos puertos cuando el atenuador está incrustado en su impedancia del sistema. Así\(\Gamma_{\text{in}} =0=\Gamma_{\text{out}}\). Dado que no hay reflexión de la carga o de la fuente, esto implica que\(S_{11}=0=S_{22}\).
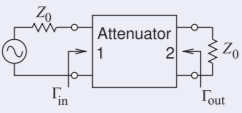
Figura\(\PageIndex{1}\)
Dado que se trata de un\(30\text{ dB}\) atenuador, la potencia entregada a la impedancia de carga\(Z_{0}\) está\(30\text{ dB}\) por debajo de la potencia disponible de la fuente, por lo tanto\(S_{21} = −30\text{ dB} = 0.0316\). El atenuador es recíproco y así\(S_{12} = S_{21}\). Así los\(S\) parámetros del atenuador son
\[\label{eq:11}\mathbf{S}=\left[\begin{array}{cc}{0}&{0.0316}\\{0.0316}&{0}\end{array}\right] \]
Obsérvese que no fue necesario conocer la impedancia de referencia para desarrollar los\(S\) parámetros.
7.3.3 Coeficiente de reflexión de entrada de una red de dos puertos terminada
En la Figura se muestra un puerto de dos puertos\(\PageIndex{1}\) que termina en el Puerto 2 en una carga con un coeficiente de reflexión\(\Gamma_{L}\). Las líneas en cada uno de los puertos son de longitud infinitesimal (es decir,\(\ell_{1}\to 0\) y\(\ell_{2}\to 0\)) y se utilizan para facilitar la visualización de la separación de la tensión en componentes de avance y retroceso. El objetivo en esta sección es desarrollar una fórmula para el coeficiente de reflexión de entrada\(\Gamma_{\text{in}} = V_{1}^{-}/V_{1}^{+}\). Para el circuito de la Figura\(\PageIndex{1}\), se pueden desarrollar tres ecuaciones:
\[\label{eq:12}V_{1}^{-}=S_{11}V_{1}^{+}+S_{12}V_{2}^{+} \]
\[\label{eq:13}V_{2}^{-}=S_{21}V_{1}^{+}+S_{22}V_{2}^{+} \]
\[\label{eq:14}V_{2}^{+}=\Gamma_{L}V_{2}^{-},\quad\text{i.e.,}\quad V_{2}^{-}=V_{2}^{+}/\Gamma_{L} \]
Tenga en cuenta que\(V_{2}^{-}\) es la onda de voltaje que sale de los dos puertos pero es incidente en la carga\(\Gamma_{L}\). El objetivo aquí es eliminar\(V_{2}^{+}\) y\(V_{2}^{-}\). Sustituir la ecuación\(\eqref{eq:14}\) en ecuación\(\eqref{eq:13}\) conduce a
\[\label{eq:15}V_{2}^{+}/\Gamma_{L}=S_{21}V_{1}^{+}+S_{22}V_{2}^{+} \]
\[\label{eq:16}V_{2}^{+}\left(\frac{1-S_{22}\Gamma_{L}}{\Gamma_{L}}\right)=S_{21}V_{1}^{+} \]
\[\label{eq:17}V_{2}^{+}=\left(\frac{S_{21}\Gamma_{L}}{1-S_{22}\Gamma_{L}}\right)V_{1}^{+} \]
Ahora sustituyendo Ecuación\(\eqref{eq:17}\) en\(\eqref{eq:12}\) Rendimientos de Ecuación
\[\label{eq:18}V_{1}^{-}=S_{11}V_{1}^{+}+S_{12}\left(\frac{S_{21}\Gamma_{L}}{1-S_{22}\Gamma_{L}}\right)V_{1}^{+} \]
y así
\[\label{eq:19}\Gamma_{\text{in}}=S_{11}+\frac{S_{12}S_{21}\Gamma_{L}}{1-S_{22}\Gamma_{L}} \]
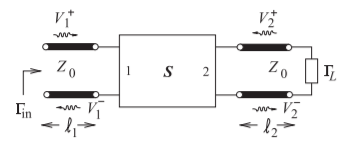
Figura\(\PageIndex{1}\): Una red de dos puertos terminada con líneas de transmisión de longitud infinitesimal en los puertos.
7.3.4 Propiedades de una Dos Partes en términos de\(S\) Parámetros
Las propiedades de mayor interés son si la red de dos puertos es sin pérdidas, pasiva o recíproca.
Si una red no tiene pérdidas, toda la entrada de energía a la red debe salir de la red. El incidente eléctrico en el Puerto 1 de una red es
\[\label{eq:20}P_{1}^{+}=\left|\frac{\frac{1}{2}V_{1}^{+}}{Z_{0}}\right|^{2} \]
y el poder que sale del Puerto 1 es
\[\label{eq:21}P_{1}^{-}=\left|\frac{\frac{1}{2}V_{1}^{-}}{Z_{0}}\right|^{2} \]
Esto se puede repetir para el Puerto 2 y el factor\(\frac{1}{2}/Z_{0}\) aparece en todas las expresiones. Entonces, al cancelar este factor, la condición para que la red no tenga pérdidas es
\[\label{eq:22}|S_{11}|^{2}+|S_{21}|^{2}=1\quad\text{and}\quad |S_{12}|^{2}+|S_{22}|^{2}=1 \]
Para que una red sea pasiva, no puede salir de la red más energía que la que la ingresa. Entonces la condición para la pasividad es
\[\label{eq:23}|S_{11}|^{2}+|S_{21}|^{2}\leq 1\quad\text{and}\quad |S_{12}|^{2}+|S_{22}|^{2}\leq 1 \]
Eso requiere la reciprocidad\(S_{21} = S_{12}\).
Notas al pie
[1] Por razones históricas se utiliza una “S” mayúscula cuando se hace referencia a\(S\) parámetros. Para la mayoría de los otros parámetros de red, se usa minúscula (por ejemplo,\(z\) parámetros para parámetros de impedancia).


