5.2: Modelado de Operaciones Asociativas en Logisim

Última actualización
Guardar como PDF

Page ID: 82930

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Para demostrar qué operadores booleanos son asociativos, el primer paso es escribir ecuaciones para cada operador que implementen dos formas asociativas para implementar una expresión, y ver si los resultados son equivalentes o no. Una primera ecuación para la operación AND podría ser la siguiente: ((A * B) * C) *D). En esta ecuación, los resultados de la salida de cada puerta AND alimentan en serie las entradas a la puerta AND siguiente, donde se corresponde con la siguiente entrada. Esto se muestra en la figura\(\PageIndex{1}\) a continuación:

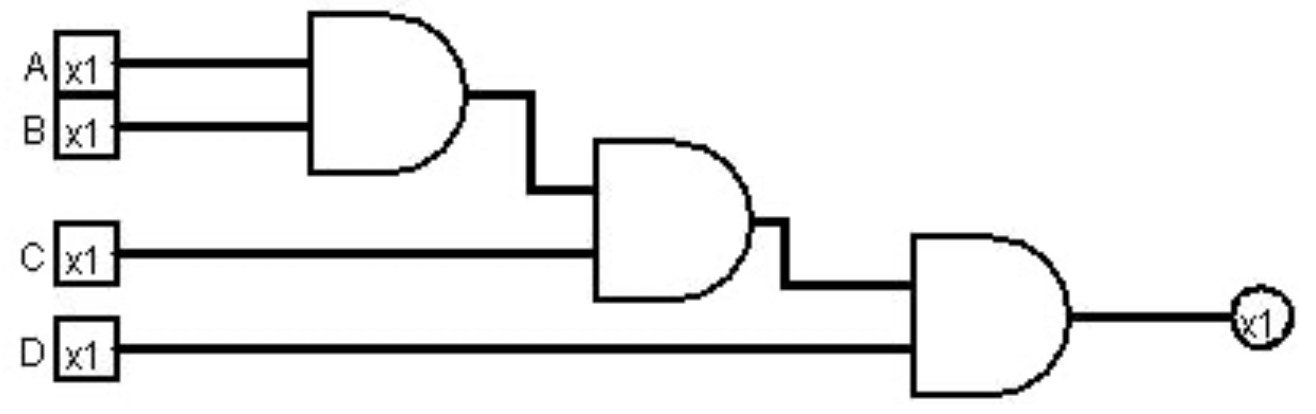
Screen Shot 2020-06-26 at 6.06.55 PM.png — Figura\(\PageIndex{1}\): Circuito Y serie

Una segunda ecuación, (A * B) * (C * D), realiza las dos primeras operaciones AND en paralelo, y luego combina los resultados, como se muestra en la Figura\(\PageIndex{2}\) siguiente:

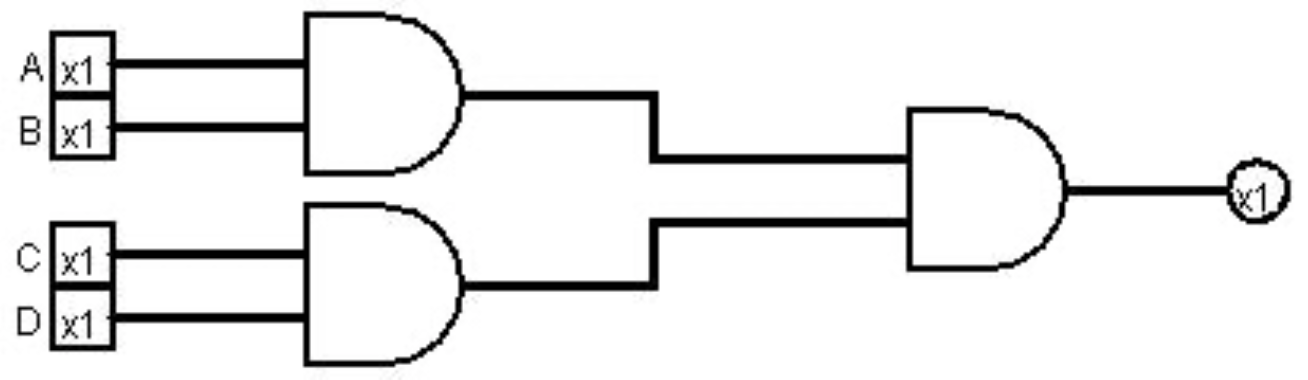
Screen Shot 2020-06-26 a las 6.08.00 PM.png — Figura\(\PageIndex{2}\): Circuito Y paralelo

Estos dos circuitos se pueden implementar en Logisim, y los resultados se utilizan para rellenar la tabla para el Ejercicio 2 en la Sección 5.5. Esto demostrará que para estas dos ecuaciones, el operador AND es asociativo. Cambiar el operador booleano insertando una puerta diferente dará resultados para el resto de la tabla.