5.11: Combinadores y Divisores
- Page ID
- 80832
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Los combinadores se utilizan para combinar energía de dos o más fuentes. Un uso típico es combinar la potencia de dos amplificadores de alta potencia para obtener una potencia más alta de la que estaría disponible de otra manera. Los divisores dividen la potencia para que la potencia de un amplificador se pueda enrutar a diferentes partes de un circuito.
5.11.1 Combinador y divisor Wilkinson
El divisor Wilkinson se puede utilizar como combinador o divisor que divide la potencia de entrada entre los puertos de salida [25]. La Figura 5.10.4 (a) es un divisor bidireccional que divide la potencia en Port\(\mathsf{1}\) por igual entre los dos puertos de salida en Puertos\(\mathsf{2}\) y\(\mathsf{3}\). Una visión particular que trajo Wilkinson fue la introducción de la resistencia entre los puertos de salida y esto actúa para suprimir cualquier desequilibrio entre las señales de salida debido a no idealidades. Si la división es exacta, no fluirá corriente en la resistencia. El circuito funciona menos bien como combinador de propósito general. Idealmente poder entrando en Puertos\(\mathsf{2}\) y\(\mathsf{3}\) se combinaría sin pérdidas y aparecería en Puerto\(\mathsf{1}\). Una aplicación típica es combinar la potencia en la salida de dos transistores emparejados donde la amplitud y la fase
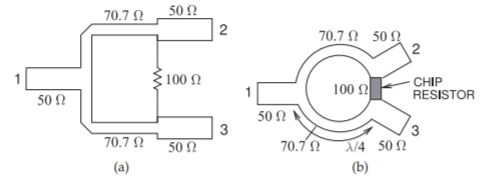
Figura\(\PageIndex{1}\): Combinador y divisor Wilkinson: (a) realización de microstrip; y (b) implementación de microstrip de mayor rendimiento.
de las señales se puede esperar que coincidan estrechamente. Sin embargo, si las señales no son idénticas, la potencia será absorbida en la resistencia. El ancho de banda del combinador/divisor Wilkinson está limitado por las líneas largas de un cuarto de longitud de onda. Sin embargo, el ancho de banda es relativamente grande, acercándose\(\pm 50\%\) [25]. También se pueden obtener relaciones de potencia arbitrarias [26, 27, 28].
El funcionamiento del divisor Wilkinson se puede ver derivando la impedancia de entrada del divisor Wilkinson bidireccional accionado en Port\(\mathsf{1}\) (ver Figura 5.10.4 (e)). Dado que el divisor Wilkinson es accionado, las señales en Puertos\(\mathsf{2}\) y\(\mathsf{3}\) serán idénticas, por lo que es como si la resistencia en el divisor Wilkinson no estuviera ahí. La impedancia de entrada de una de las secciones largas de un cuarto de longitud de onda en la Figura 5.10.4 (e) es
\[\label{eq:1}Z_{1}=\frac{(\sqrt{2}Z_{0})^{2}}{Z_{0}}=2Z_{0} \]
y así el modelo de Wilkinson se reduce al de la Figura 5.10.4 (f). Las dos\(2Z_{0}\) resistencias están en paralelo, resultando en las reducciones adicionales del modelo en las Figuras 5.10.4 (g) y 5.10.4 (h). Por lo tanto, Port\(\mathsf{1}\) está emparejado. Un análisis similar muestra que los puertos\(\mathsf{2}\) y\(\mathsf{3}\) están emparejados (tienen una impedancia de entrada de\(Z_{0}\)). Por lo tanto, los\(S\) parámetros del divisor de potencia Wilkinson bidireccional con una división igual de la potencia de salida son
\[\label{eq:2}\mathbf{S}=\left[\begin{array}{ccc}{0}&{-\jmath /\sqrt{2}}&{-\jmath /\sqrt{2}}\\{-\jmath /\sqrt{2}}&{0}&{0}\\{-\jmath/\sqrt{2}}&{0}&{0}\end{array}\right] \]
La Figura 5.10.4 (b) es una representación compacta del divisor Wilkinson bidireccional, y un divisor Wilkinson de tres vías se muestra en la Figura 5.10.4 (d). Este patrón se puede repetir para producir división de potencia\(N\) -way. La versión de elementos agrupados del divisor Wilkinson que se muestra en la Figura 5.10.4 (c) se basa en el\(LC\) modelo de un segmento de línea de transmisión de un cuarto de longitud de onda larga. Con una impedancia\(50\:\Omega\) del sistema y frecuencia central de\(400\text{ MHz}\), los elementos del elemento agrupado son (de la Figura 2-37 (c))\(L = 28.13\text{ nH, }C_{1} = 11.25\text{ pF, }C_{2} = 5.627\text{ pF,}\) y\(R = 100\:\Omega\).
La Figura\(\PageIndex{1}\) (a) es la disposición de una realización directa de microcinta de un divisor Wilkinson. El problema obvio es cómo incorporar la resistencia. Siempre y cuando la resistencia se coloque simétricamente esto no es un problema tan grave como inicialmente parecería, ya que la potencia no se disipa en la resistencia a menos que haya un desequilibrio. En la Figura\(\PageIndex{1}\) (b) se muestra un diseño de microcinta de mayor rendimiento, donde las líneas de transmisión están curvadas para acercar los puertos de salida entre sí de manera que se pueda usar una resistencia de chip.
Ejemplo\(\PageIndex{1}\): Lumped-Element Wilkinson Divider
Diseñe un divisor Wilkinson de 2 vías con elementos grumados en un\(60\:\Omega\) sistema. La frecuencia central del diseño debe ser\(10\text{ GHz}\).
Solución
El diseño comienza con la forma de línea de transmisión del divisor Wilkinson que se convertirá en una forma de elemento grumo-último. Los parámetros de diseño son\(Z_{0} = 60\:\Omega,\)\(f = 10\text{ GHz, }\)\(\omega = 2\pi 10^{10} = 2.283\cdot 10^{10}\text{ rads/s}\) y así
\[Z_{01}=\sqrt{2}Z_{0}=84.85\:\Omega,\quad R=2Z_{0}=120\:\Omega\nonumber \]
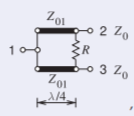
Figura\(\PageIndex{2}\)
La siguiente etapa es convertir las líneas de transmisión en elementos agrupados. Un diseño de banda ancha de una línea de transmisión de cuarto de longitud de onda se presentó en la Figura 2-37 (b) de [15]. Es decir, cada una de las líneas de cuarto de onda tiene el modelo
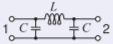
Figura\(\PageIndex{3}\)
con
\[\begin{aligned} L &= Z_{01}/\omega = 84.85/\omega = 954.9\text{ pH}\nonumber \\ C &= 1/(Z_{01}\omega )=1/(84.85\omega ) = 265.3\text{ fF}\nonumber\end{aligned}\nonumber \]
Así que el diseño final del elemento agrupado es
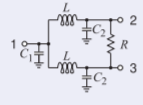
Figura\(\PageIndex{4}\)
con
\[\begin{aligned} C_{1}&=2C=530.6\text{ fF}\nonumber \\ C_{2}&=C=265.3\text{ fF}\nonumber \\ L&=954.9\text{ pH}\nonumber \\ R&=120\:\Omega\nonumber\end{aligned}\nonumber \]
5.11.2 Combinador Chireix
Uno de los problemas con la estructura de Wilkinson cuando se usa como combinador es que solo es eficiente en la combinación cuando las dos señales a combinar están en fase. Un mejor combinador es el combinador Chireix [29] que se muestra en la Figura 5.12.1. Este combinador se suele utilizar cuando se combinan las salidas de dos amplificadores logrando una combinación eficiente incluso cuando las señales a combinar no son idénticas [30, 31, 32, 33].

