5.12: Transformador de Línea de Transmisión
- Page ID
- 80811
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Uno de los desafíos en la ingeniería de RF es lograr la operación de banda ancha de transformadores desde megahercios hasta varios gigahercios. En esta sección se presentan varias estructuras que operan como transformadores magnéticos a frecuencias inferiores a varios cientos de megahercios pero como estructuras de líneas de transmisión acopladas a altas frecuencias. Un transformador que logre esto y,
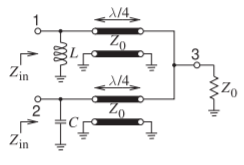
Figura\(\PageIndex{1}\): Combinador Chireix.
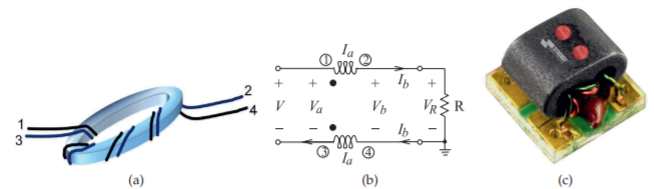
Figura\(\PageIndex{2}\): Un balun RF de banda ancha como líneas acopladas enrolladas alrededor de un núcleo de ferrita: (a) realización física (los cables\(1–2\) y\(3–4\) forman una sola línea de transmisión); (b) circuito equivalente que usa un transformador bobinado de alambre (el número de devanados primario y secundario es igual); y (c) empaquetado como un módulo (Modelo TM1-9 con un rango de frecuencia de\(100–5000\text{ MHz}\). Copyright Synergy Microwave Corporation, utilizada con permiso [34]).

Figura\(\PageIndex{3}\): Transformador de núcleo abierto para montaje en superficie. Copyright 2012 Scientific Components Corporation d/b/a Mini-Circuitos, utilizados con permiso [11].
en esta configuración, se da cuenta de que un balun se muestra en la Figura\(\PageIndex{2}\) (a). Por debajo de unos cientos de megahercios esto funciona como un transformador magnético. Por encima de esta frecuencia el núcleo de ferrita no puede responder a la señal y el circuito magnético a través del núcleo aparece como un circuito abierto. Entonces, dado que el transformador ya no está funcionando como un transformador magnético, la fuga magnética es intrascendente. A altas frecuencias, las líneas de transmisión por cable están estrechamente acopladas y aparecen como un acoplador perfecto si las líneas (o cables aquí) son lo suficientemente largas. El circuito equivalente de esta estructura se muestra en la Figura\(\PageIndex{2}\) (b). A altas frecuencias, las capacitancias parásitas entre los devanados se vuelven importantes pero se convierten en parte de la capacitancia de la línea de transmisión. Muchos tipos de transformadores que operan desde varios megahercios hasta varios gigahercios se pueden realizar usando el mismo principio y están disponibles como componentes de montaje en superficie (consulte la Figura\(\PageIndex{2}\) (c)).
El acoplamiento de alta frecuencia se mejora retorciendo los conductores como se muestra en la Figura\(\PageIndex{3}\). La combinación de acoplamiento magnético a bajas frecuencias con acoplamiento de línea de transmisión a altas frecuencias produce un transformador que opera en anchos de banda muy amplios.
5.12.1 Transformador de Línea de Transmisión como Balun
El esquema de un balun\(1:1\) RF de banda ancha se muestra en la Figura\(\PageIndex{2}\) (b) y una realización del mismo se muestra en la Figura\(\PageIndex{2}\) (a y c). La\(1:1\) designación indica que no hay transformación de impedancia. Las ecuaciones de circuito que describen este balun son (a partir de los\(ABCD\) parámetros de una línea de transmisión; ver Tabla 2.2.1)
\[\label{eq:1} V_{a} = V_{b}\cos(\beta\ell ) + \jmath I_{b} Z_{0} \sin(\beta\ell)\quad\text{and}\quad I_{a} = I_{b}\cos(\beta\ell ) + \jmath\frac{V_{b}}{Z_{0}}\sin(\beta\ell) \]
y la resistencia a la carga crea una tercera ecuación,
\[\label{eq:2}V_{b}=I_{b}R \]
El objetivo a continuación es el desarrollo de una ecuación de diseño que describa las propiedades esenciales de la estructura. Sustituir la ecuación\(\eqref{eq:2}\) en la ecuación\(\eqref{eq:1}\) conduce a
\[\label{eq:3}V_{a}=V_{b}\left[\cos(\beta\ell)+\jmath\frac{Z_{0}}{R}\sin(\beta\ell)\right]\quad\text{and}\quad I_{a}=\frac{V_{b}}{R}\left[\cos(\beta\ell)+\jmath\frac{R}{Z_{0}}\sin(\beta\ell)\right] \]
Elegir\(Z_{0} = R\) rendimientos (ya que\(\text{e}^{\jmath\beta\ell} = \cos(\beta\ell) + \jmath\sin(\beta\ell)\))
\[\label{eq:4}V_{a}=V_{b}\text{e}^{\jmath\beta\ell}\quad\text{and}\quad I_{a}=(V_{b}/R)\text{e}^{\jmath\beta\ell} \]
y así
\[\label{eq:5}Z_{\text{in}}=V_{a}/I_{a}=R \]
Este análisis es idealizado, ya que se eliminan los parásitos (principalmente capacitancias parasitarias), pero la ecuación anterior indica que la función esencial de la estructura es la de un balun sin transformación de impedancia. La disposición de transformadores mostrada en la Figura\(\PageIndex{2}\) (b) es de particular interés ya que se puede realizar usando líneas de transmisión acopladas.
5.12.2 Transformador de\(4:1\) impedancia a altas frecuencias
Al cambiar la conexión de los terminales del transformador es posible lograr la transformación de impedancia. Un transformador de\(4:1\) impedancia se muestra en la Figura\(\PageIndex{4}\) (a). Una disposición específica de los devanados primario y secundario pone esto en lo que se llama la forma de línea de transmisión, que se muestra en la Figura\(\PageIndex{5}\). A altas frecuencias se hacen cumplir las condiciones de puerto de manera que las corrientes en Puertos\(\mathsf{1}\) y\(\mathsf{3}\) (y en Puertos\(\mathsf{2}\) y\(\mathsf{4}\)) se correspondan, como se muestra en la Figura\(\PageIndex{5}\). Mostrando que\(Z_{\text{in}} = R\) comienza con
\[\label{eq:6}\begin{array}{ll}{V_{a} = V_{b} \cos(\beta\ell ) + \jmath I_{b}Z_{0} \sin(\beta\ell )}&{I_{a} = I_{b} \cos(\beta\ell) + \jmath \frac{V_{b}}{Z_{0}} \sin(\beta\ell )}\\{V_{\text{in}}=V_{a}+R(I_{a}+I_{b}),\quad\text{and}}&{V_{b}=(I_{a}+I_{b})R}\end{array} \]
Por lo que el objetivo es encontrar\(Z_{\text{in}} = V_{\text{in}}/I_{a}\), ya que esto define la función eléctrica requerida. Ahora
\[\label{eq:7}V_{\text{in}}=V_{a}+V_{b}=V_{b}[1+\cos(\beta\ell)]+\jmath I_{b}Z_{0}\sin(\beta\ell) \]
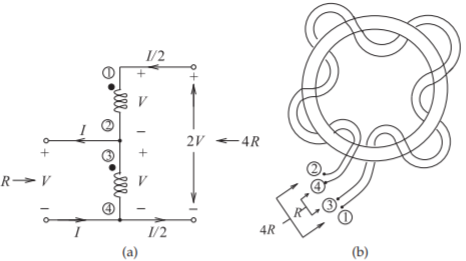
Figura\(\PageIndex{4}\): Un transformador de\(4:1\) impedancia: (a) Esquema (las bobinas tienen el mismo número de devanados); y (b) realización como transformador con cables acoplados retorcidos alrededor de un núcleo magnético.
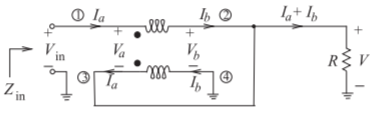
Figura\(\PageIndex{5}\): Una forma de línea de transmisión del transformador de\(4:1\) impedancia de la Figura\(\PageIndex{4}\), después de [35]. (El número de devanados primarios y secundarios son los mismos.)
y usando las ecuaciones anteriores
\[\begin{align}I_{a}&=I_{b}\cos(\beta\ell)+\jmath(I_{a}+I_{b})\frac{R}{Z_{0}}\sin(\beta\ell)\nonumber \\ \label{eq:8}I_{b}&=I_{a}\frac{Z_{0}-\jmath R\sin(\beta\ell)}{Z_{0}\cos(\beta\ell)+\jmath R\sin(\beta\ell)}\end{align} \]
Así
\[\label{eq:9}Z_{\text{in}}=\frac{V_{\text{in}}}{I_{a}}=Z_{0}\frac{2R[1 + \cos(\beta\ell)] + \jmath Z_{0} \sin(\beta\ell)}{Z_{0} \cos(\beta\ell) + \jmath R \sin(\beta\ell )} \]
A frecuencias muy bajas la longitud eléctrica de la línea de transmisión\(\beta\ell\),, es insignificante y pequeña\(Z_{\text{in}} = 4R\). Para ver qué sucede cuando la longitud de la línea de transmisión tiene un efecto significativo, considere el caso especial cuando\(Z_{0} = 2R\), entonces
\[\label{eq:10}Z_{\text{in}}=2R(1+\text{e}^{-\jmath\beta\ell}) \]
Para una línea corta, es decir,\(\ell < 0.1\lambda\) o\(\beta\ell < 0.2\pi\), La ecuación se\(\eqref{eq:10}\) puede aproximar como
\[\label{eq:11}Z_{\text{in}}\approx 2R[1+1-\jmath\beta\ell]=4R-\jmath R(2\beta\ell) \]
El componente imaginario\(−\jmath R2\beta\ell\),, es una capacitancia y debe ser resonada (por ejemplo, por un inductor en serie) para obtener la transformación de resistencia requerida.
El enfoque general descrito anteriormente se puede utilizar para diseñar transformadores con relaciones de impedancia más altas. Dos más, un\(9:1\) transformador y un\(16:1\) transformador, se muestran en la Figura\(\PageIndex{6}\).
Una práctica realización de línea de transmisión de banda ancha del\(4:1\) transformador se muestra en la Figura\(\PageIndex{4}\) (b), donde la línea de transmisión es un par de cables trenzados.
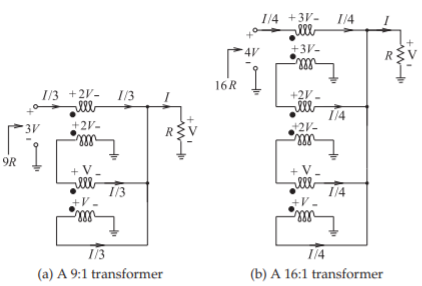
Figura\(\PageIndex{6}\): Transformadores de impedancia de alto orden.
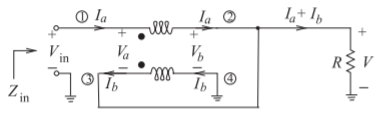
Figura\(\PageIndex{7}\): Esquema de baja frecuencia del transformador de\(4:1\) impedancia mostrado en la Figura\(\PageIndex{4}\) (a).
5.12.3 Transformador de\(4:1\) impedancia a bajas frecuencias
En la sección anterior se mostró que el transformador de impedancia de la Figura\(\PageIndex{4}\) (a) actúa como un transformador de\(4:1\) impedancia a altas frecuencias donde la estructura puede considerarse como una línea de transmisión. En esta sección se mostrará que el transformador también es un transformador de\(4:1\) impedancia a bajas frecuencias donde la estructura puede considerarse como un transformador de alambre enrollado.
A bajas frecuencias, las condiciones de puerto\(^{1}\) en los extremos de la línea de transmisión no se hacen cumplir y por lo tanto se muestra una mejor representación de baja frecuencia de las corrientes del transformador en la Figura\(\PageIndex{7}\). Si a bajas frecuencias el transformador de la Figura\(\PageIndex{5}\) tiene una autoinductancia de\(L_{s}\) y una inductancia mutua de\(M\), entonces las ecuaciones de circuito para el transformador son
\[\begin{align}\label{eq:12}V_{\text{in}}-V_{b}&=\jmath\omega L_{s}I_{a}-\jmath\omega MI_{b}\\ \label{eq:13}V_{b}&=-\jmath\omega L_{s}I_{b}+\jmath\omega MI_{a} \\ \label{eq:14}V_{b}&=(I_{a}+I_{b})R\end{align} \]
Ecuación de ecuaciones\(\eqref{eq:13}\) y\(\eqref{eq:14}\) y reorganización,
\[\label{eq:15}I_{b}=-\left(\frac{R-\jmath\omega M}{R+\jmath\omega L_{s}}\right)I_{a} \]
Combinando ecuaciones\(\eqref{eq:12}\)\(\eqref{eq:14}\) y reordenando,
\[\label{eq:16}V_{\text{in}}=(R+\jmath\omega L_{s})I_{a}+(R-\jmath\omega M)I_{b} \]
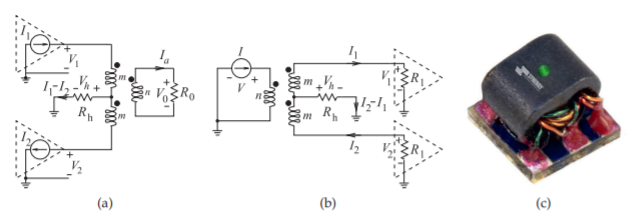
Figura\(\PageIndex{8}\): Un transformador\(180^{\circ}\) híbrido: (a) utilizado como combinador; (b) usado como divisor; y (c) transformador de toma central como componente de montaje en superficie (Modelo TM1-2 con un rango de frecuencia de\(20–1200\text{ MHz}\). Copyright Synergy Microwave Corporation, utilizada con permiso [34]).
Sustitución\(I_{b}\) en Ecuación\(\eqref{eq:16}\) usando\(\eqref{eq:15}\) rendimientos de Ecuación
\[\label{eq:17}V_{\text{in}}=\left[(R+\jmath\omega L_{s})-\frac{(R-\jmath\omega M)^{2}}{R+\jmath\omega L_{s}}\right]I_{a} \]
Por lo tanto, la impedancia de entrada es
\[\label{eq:18}Z_{\text{in}}=\frac{V_{\text{in}}}{I_{a}}=\frac{R^{2} + \jmath 2R\omega L_{s} − (\omega L_{s})^{2} − R^{2} + \jmath 2R\omega M + (\omega M)^{2}}{R+\jmath\omega L_{s}} \]
Si se asume el acoplamiento ideal (es decir,\(M = L_{s}\)) entonces la ecuación se\(\eqref{eq:18}\) reduce a
\[\label{eq:19}Z_{\text{in}}=\frac{\jmath 4R\omega L_{s}}{R+\jmath\omega L_{s}} \]
Si\(\jmath\omega L_{s} ≫ R\), entonces
\[\label{eq:20}Z_{\text{in}}\approx 4R \]
Así, el transformador es un transformador de\(4:1\) impedancia tanto a bajas frecuencias cuando la estructura actúa como un transformador magnético como, como se ve en la Sección 5.12.2, a frecuencias más altas cuando la estructura actúa como una línea de transmisión. El diseño del transformador de impedancia se dirige entonces a administrar la región de transición de frecuencia y garantizar que la transformación de impedancia requerida ocurra allí también. En la práctica, la operación muy de banda ancha no es difícil de lograr.
5.12.4 Transformador híbrido utilizado como combinador
En la Figura\(\PageIndex{8}\) (a) se utiliza un transformador\(180^{\circ}\) híbrido para combinar las salidas de dos amplificadores de potencia que son accionados\(180^{\circ}\) fuera de fase uno con respecto al otro. Esto se hace comúnmente cuando la potencia disponible de un solo amplificador de transistor de estado sólido no es suficiente para cumplir con los requisitos de energía. Dado que la suma de los amperios-vueltas de un transformador ideal debe ser cero,
\[\label{eq:21}nI_{o}=m(I_{1}+I_{2}) \]
Ejemplo\(\PageIndex{1}\): Transformer Design
La impedancia de salida equivalente Thevenin de cada amplificador en la Figura\(\PageIndex{8}\) (a) es\(1\:\Omega\) y la impedancia del sistema,\(R_{0}\), es\(50\:\Omega\). Elija los devanados del transformador para la máxima transferencia de potencia.
Solución
Para la transferencia máxima de potencia\(R_{\text{in}} = 1\:\Omega\), y así de la ecuación\(\eqref{eq:21}\),
\[\label{eq:22}1=\left(\frac{m}{n}\right)^{2}\cdot 2\cdot 50\quad\text{and}\quad\frac{m}{n}=0.1 \]
Así, con una relación de\(10:1\) devanado se puede lograr la transformación de impedancia requerida.
5.12.5 Transformador híbrido utilizado como divisor de potencia
El transformador híbrido también se puede utilizar para dividir la energía de una fuente para impulsar dos cargas. El circuito de la Figura\(\PageIndex{8}\) (b) divide la potencia de un controlador de fuente de corriente en dos cargas. Con el número de devanados primario y secundario igual (es decir,\(m = n\)), las ecuaciones del circuito son
\[\label{eq:23}I = I_{1} + I_{2},\quad V_{1} = V + V_{h},\quad \text{and}\quad V_{2} = V_{h} − V \]
Así
\[\label{eq:24}V_{1}-V_{h}=V_{h}-V_{2} \]
Usando\(V_{1} = R_{1}I_{1},\: V_{2} = −I_{2}R_{2},\) y\(V_{h} = (I_{2} − I_{1})R_{h},\) se obtienen las características eléctricas deseadas del divisor:
\[\label{eq:25}\frac{I_{2}}{I_{1}}=\frac{R_{1}+2R_{h}}{R_{2}+2R_{h}} \]
Se pueden hacer varias observaciones sobre el rendimiento del divisor de potencia. Si\(R_{1} = R_{2}\), entonces\(I_{1} = I_{2}\) por cualquier valor de\(R_{h}\). Por el contrario, si\(R_{1}\neq R_{2},\: I_{1}\neq I_{2}\) por un finito\(R_{h}\). Para obtener corrientes de accionamiento iguales en ambos amplificadores de potencia a pesar de las variaciones en\(R_{1}\) y\(R_{2}\), la toma central del transformador debe omitirse para que\(R_{h} = ∞\).
5.12.6 Combinador híbrido de banda ancha
Un combinador híbrido de banda ancha se muestra en la Figura\(\PageIndex{9}\). En lo que sigue, se demuestra que este combinador tiene la propiedad de acomodar desajustes de los amplificadores. El desarrollo comienza asumiendo que los transformadores tienen igual número de vueltas en cada devanado. Estos dos transformadores se utilizan para hacer un acoplador híbrido de banda ancha (transformador de línea de transmisión). Las ecuaciones de circuito son
\[\begin{align} \label{eq:26}I_{1}=I_{a}+I_{b}\quad &\text{and}\quad I_{2}=I_{a}-I_{b} \\ \label{eq:27} I_{a}=\frac{1}{2}(I_{1}+I_{2})\quad &\text{and}\quad I_{b}=\frac{1}{2}(I_{1}-I_{2}) \\ \label{eq:28}V_{1}=\frac{V_{o}}{2}+V_{h}\quad &\text{and}\quad V_{2}=\frac{V_{o}}{2}-V_{h}\end{align} \]
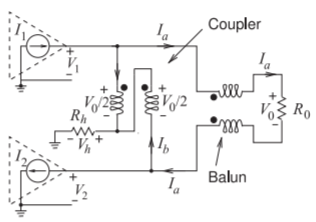
Figura\(\PageIndex{9}\): Combinador de potencia híbrido de banda ancha.
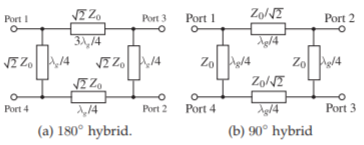
Figura\(\PageIndex{10}\): Topologías de híbridos de tipo anillo.
Así
\[\begin{align}\label{eq:29}\frac{V_{1}}{I_{1}}&=R_{h}\left(1-\frac{I_{2}}{I_{1}}\right)+\frac{R_{0}}{2}\left(1-\frac{I_{2}}{I_{1}}\right) \\ \label{eq:30}\frac{V_{2}}{I_{2}}&=\frac{R_{0}}{2}\left(1+\frac{I_{1}}{I_{2}}\right)-R_{h}\left(\frac{I_{1}}{I_{2}}-1\right)\end{align} \]
Una situación especial es cuándo\(R_{h} = R_{0}/2\), y entonces\(V_{2}/I_{2} = R_{0}\) y\(V_{1}/I_{1} = R_{0}\). Así cada uno de los amplificadores ve una resistencia de carga constante\(R_{0}\), aunque los amplificadores no coincidan, dando como resultado, por ejemplo, cuando los amplificadores tienen ganancias ligeramente diferentes.
Notas al pie
[1] Las corrientes en el par de terminales de un puerto son iguales en magnitud y opuestas en dirección.

