5.13: Híbridos Basados en Línea de Transmisión
- Page ID
- 80818
Los híbridos se pueden realizar en una variedad de estructuras de líneas de transmisión. Algunas de estas, pero representativas, se discuten aquí. Los híbridos también se pueden realizar usando elementos grumados modelando los segmentos de línea de transmisión.
5.13.1 Híbridos ramificados basados en líneas de transmisión
Un híbrido de línea bifurcada se basa en segmentos de línea de transmisión que introducen retardo de fase. Dos de estos híbridos se muestran en la Figura 5.12.10 donde las diferentes trayectorias de señal dan como resultado una interferencia constructiva y destructiva de las señales. Esta es una forma muy diferente de realizar la función híbrida a la obtenida mediante transformadores magnéticos. El funcionamiento del\(180^{\circ}\) híbrido (Figura 5.12.10 (a)) puede verificarse aproximadamente contando el número total de desplazamientos de\((90^{\circ})\) fase de un cuarto de longitud de onda en cada trayectoria. No es tan fácil verificar el funcionamiento del\(90^{\circ}\) híbrido. Las diversas impedancias características de los segmentos de línea de transmisión ajustan los niveles de las señales. El funcionamiento del\(90^{\circ}\) híbrido se examina en el ejemplo de esta sección. (Se podría hacer un análisis completo usando gráficos de flujo de señal).
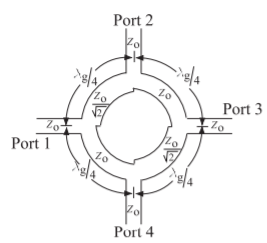
Figura\(\PageIndex{1}\): Implementación plana del híbrido de ramificación\(3\text{ dB}\) tipo anillo con la topología de la Figura 5.12.10 (b).
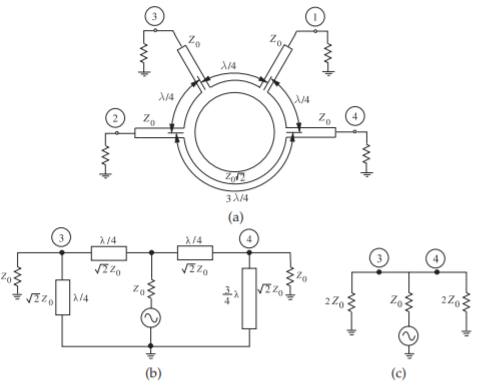
Figura\(\PageIndex{2}\): Híbrido RAT-RACE con entrada en Puerto\(\mathsf{1}\), salidas en Puertos\(\mathsf{3}\) y\(\mathsf{4}\), y tierra virtual en Puerto\(\mathsf{2}\): (a) implementación como circuito plano; (b) modelo de línea de transmisión; y (c) modelo de circuito equivalente.
Estos híbridos ramificados pueden formarse en forma de anillo, como se muestra en la Figura\(\PageIndex{1}\). También vale la pena considerar el llamado circuito de raza rata o anillo híbrido que se muestra en la Figura\(\PageIndex{2}\) (a). Las señales de salida de Puertos\(\mathsf{2}\) y\(\mathsf{4}\) difieren en fase por\(180^{\circ}\) (en contraste con el acoplador de línea bifurcada, donde está la diferencia de fase\(90^{\circ}\)). Una característica de diseño interesante e importante surge al considerar la acción del transformador de cuarto de onda de este acoplador. Sólo Puertos\(\mathsf{2}\) y\(\mathsf{4}\) exhiben esta acción, ya que el Puerto\(\mathsf{3}\) es de media onda separado del puerto de alimentación de entrada\(\mathsf{1}\). De esta manera la carga neta efectiva en las líneas de anillo interior que alimentan Puertos\(\mathsf{2}\) y\(\mathsf{4}\) asciende a\(2Z_{0}\) (dos\(Z_{0}\) cargas que aparecen, equivalentemente, en serie). Ahora la impedancia característica\(Z_{0}\) de cualquier línea transformadora de cuarto de onda entre dos impedancias,\(Z_{01}\) y\(Z_{02}\), es igual a\(\sqrt{Z_{01}Z_{02}}\). En este caso las dos impedancias son\(Z_{0}\) y\(2Z_{0}\), respectivamente, entonces (de la Sección 2.4.6 de [15]) la impedancia de entrada de la línea intermedia de cuarto de onda es
\[\label{eq:1} Z_{0}'=\sqrt{Z_{0}\cdot 2Z_{0}}=\sqrt{2}Z_{0} \]
Así, la impedancia característica de la línea que forma el propio anillo es\(\sqrt{2}\) multiplicada por la impedancia de la línea de alimentación. Entonces, cuando la impedancia de todos los puertos es\(50\:\Omega\), la impedancia característica del anillo es\(70.7\:\Omega\).
Ejercicio\(\PageIndex{1}\): Rat-Race Hybrid
En este ejemplo se considera el circuito rata-carrera mostrado en la Figura\(\PageIndex{2}\) (a). Una de las funciones de este circuito es que con una entrada en Puerto\(\mathsf{1}\), la potencia de esta señal se divide entre Puertos\(\mathsf{3}\) y\(\mathsf{4}\). Al mismo tiempo, no aparece ninguna señal en el Puerto\(\mathsf{2}\). Este ejemplo es un ejercicio para explotar las propiedades de transformación de impedancia de la línea de transmisión.
De la Figura\(\PageIndex{2}\) (a) se observa que cada puerto está separado del otro puerto por una longitud eléctrica específica. Intuitivamente uno puede darse cuenta de que habrá varias salidas posibles para la excitación desde diferentes puertos. Se estudiará cada caso.
Cuando el Puerto\(\mathsf{1}\) del híbrido está excitado o accionado, las salidas en Puertos\(\mathsf{3}\) y\(\mathsf{4}\) están en fase, ya que ambos están distanciados de Puerto\(\mathsf{1}\) por una longitud eléctrica de\(\lambda_{g}/4\), mientras que Puerto\(\mathsf{2}\) permanece aislado, como la longitud eléctrica de los dos caminos de Puerto\(\mathsf{1}\) a Puerto\(\mathsf{2}\) difieren en un múltiplo par de\(\lambda_{g}/2\). Así Port\(\mathsf{2}\) será un cortocircuito eléctrico a la señal en Port\(\mathsf{1}\).
De manera similar, una señal excitada en Port\(\mathsf{2}\) dará como resultado salidas en Puertos\(\mathsf{3}\) y\(\mathsf{4}\), aunque con una diferencia de fase de\(180^{\circ}\) entre los dos puertos de salida y Port\(\mathsf{1}\) permanece aislada.
Por último, una señal excitada en Puertos\(\mathsf{3}\) y\(\mathsf{4}\) dará como resultado la suma de las dos señales en Puerto\(\mathsf{1}\) y la diferencia de dos señales en Puerto\(\mathsf{2}\). Esta combinación de salida se debe nuevamente a la variación de la longitud eléctrica entre cada puerto y cada otro puerto en el híbrido rata-raza. El modelo de línea de transmisión equivalente y el circuito equivalente del híbrido rata-carrera se muestran en las Figuras\(\PageIndex{2}\) (b y c), respectivamente.
5.13.2 Híbridos de Elementos Lumped-Element
Los híbridos se desarrollan en base a principios de líneas de transmisión, pero es posible crear híbridos utilizando equivalentes de elementos grumosos de segmentos de línea de transmisión. En algunos casos, el círculo completo de diseño puede comenzar con la conceptualización del transformador magnético, seguido de una realización de la línea de transmisión, y luego una aproximación de elementos agrupados. Al menos esto es válido sobre un ancho de banda centrado en una frecuencia particular,\(f = \omega_{0}/(2\pi )\). El equivalente de elementos grumosos del\(180^{\circ}\) híbrido en la Figura 5.12.10 (a) se muestra en la Figura\(\PageIndex{3}\) (a) con
\[\label{eq:2}\omega_{0}L=\frac{1}{\omega_{0}C}=\sqrt{2}Z_{0} \]
Este resultado proviene del circuito equivalente de banda ancha de una\(\lambda /4\) línea mostrada en la Figura 2-37. El híbrido en cuadratura de elementos grumosos de la Figura\(\PageIndex{3}\) (b), basado en la Figura 5.12.10 (b), tiene
\[\label{eq:3}\omega_{0}Z_{0}C_{a}=1,\quad C_{a}+C_{b}=\frac{1}{\omega_{0}^{2}L},\quad\text{and}\quad \omega_{0}L=\frac{Z_{0}}{\sqrt{2}} \]
donde\(Z_{0}\) esta la impedancia del puerto.
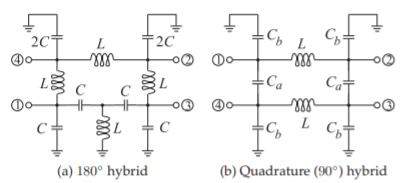
Figura\(\PageIndex{3}\): Híbridos de elementos grumosos.

