5.3: Elementos Agrupados Integrados
- Page ID
- 80826
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Esta sección considera elementos grumados utilizados en circuitos integrados que operan a frecuencias de microondas. Los elementos agrupados como condensadores, inductores y resistencias rara vez pueden considerarse como elementos puros a frecuencias de microondas. Los inductores y capacitores tienen pérdidas significativas y todos los elementos almacenan energía tanto en forma eléctrica como magnética.
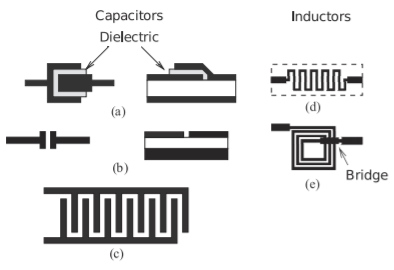
Figura\(\PageIndex{1}\): Elementos agrupados monolíticos: (a) condensador de placa paralela; (b) condensador de hueco; (c) condensador interdigitado; (d) inductor de línea de meandro; y (e) inductor espiral.
5.3.1 Capacitores en chip
Hay tres formas primarias de condensador en chip:
- Condensador metal-dieléctrico-metálico—usando metalización de interconexión.
- Condensador metal-dieléctrico-semiconductor: esencialmente un transistor MOS.
- Condensador de unión de semiconductores: ya sea la capacitancia de una\(pn\) unión polarizada inversa o una barrera Schottky.
En la tecnología de silicio es común referirse al primer tipo de condensador como un condensador de metal-óxido-metal (MOM) o como un condensador metal-aislador-metal (MIM). Un condensador MOM se puede realizar como una capacitancia de placa paralela (ver Figura\(\PageIndex{1}\) (a)), y se pueden usar múltiples niveles de metalización para aumentar la densidad de capacitancia. Normalmente\(500\text{ fF/}\mu\text{m}^{2}\) están disponibles valores de capacitancia relativamente bajos de hasta.
Una capacitancia MOM alternativa está disponible usando arreglos laterales de conductores en la misma capa (ver Figura\(\PageIndex{1}\) (b)); es decir, las estructuras metálicas adyacentes están separadas por un pequeño espacio horizontal. Nuevamente, hay dos conexiones metálicas distintas, y se puede obtener una separación de metales más pequeña usando fotolitografía que la posible usando separación dieléctrica. Sin embargo, la densidad de capacitancia solo se incrementa en un factor de aproximadamente tres. Los valores más altos se pueden obtener utilizando el condensador interdigitado (IDC) de la Figura\(\PageIndex{1}\) (c). Ambos tipos de capacitancia MOM, placa paralela y lateral, están definidos geométricamente, son independientes de voltaje, tienen coeficientes de temperatura muy bajos y tienen tolerancias de fabricación iniciales de\(20\%–30\%\).
El segundo tipo de condensador en la tecnología MOS se conoce como un condensador de metal-óxido-semiconductor (MOS). Los capacitores MOS utilizan un transistor MOS con una capacitancia de placa paralela entre la puerta de un transistor MOS y un canal fuertemente invertido. El drenaje y la fuente están conectados en esta configuración y la separación entre los conductores es delgada, siendo el espesor del óxido de la puerta. Esto conduce a altos valores de capacitancia, aunque con una dependencia de voltaje débil. La capacitancia de unión se realiza como la capacitancia de una unión semiconductora con polarización inversa. Esta capacitancia puede ser bastante grande, pero tiene una fuerte dependencia de voltaje. Esta dependencia de voltaje se puede utilizar para realizar circuitos sintonizables (por ejemplo, un oscilador controlado por voltaje).
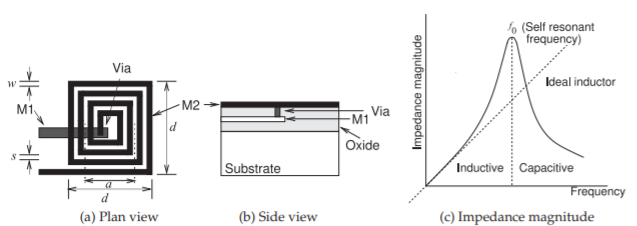
Figura\(\PageIndex{2}\): Un inductor en espiral en chip.
5.3.2 Inductores Planares
Los inductores son componentes importantes en los circuitos de RF y microondas. Además de su papel en las redes coincidentes, se utilizan para proporcionar sesgo a dispositivos activos mientras bloquean efectivamente las señales de RF de los circuitos de polarización. Los inductores de hasta\(10\text{ nH}\) pueden fabricarse en forma compacta, siendo típico el inductor espiral de la Figura\(\PageIndex{1}\) (e). Los alambres de unión también se pueden usar para realizar pequeñas inductancias en el\(0.5–1\text{ nH}\) rango. Una de las ventajas de tener una porción de una gran inductancia en el chip es la sensibilidad reducida a las conexiones de conexión de matriz (cable de unión, etc.) utilizadas para conectarse a una inductancia externa. Los valores pequeños de inductancia pueden ser realizados por el inductor de línea de meandro de la Figura\(\PageIndex{1}\) (d). Esto se basa en una longitud de línea de alta impedancia (línea estrecha en microcinta) que aparece inductiva.
Un inductor espiral en chip se muestra en la Figura\(\PageIndex{2}\). Una expresión aproximada para la inductancia de esta estructura fue desarrollada por Wheeler [1, 2, 3]:
\[\label{eq:1}L\approx\frac{9.4\mu_{0}n^{2}a^{2}}{11d-7a} \]
donde\(a\) es el radio medio de la espiral y\(n\) es el número de vueltas. Esta fórmula se derivó para bobinas circulares, pero su precisión para espirales cuadradas está dentro\(5\%\) de los valores obtenidos mediante simulación EM [4]. Por lo tanto, es una fórmula muy útil en las primeras etapas del diseño, pero se requiere el análisis EM para obtener la precisión y dependencia de frecuencia necesarias del inductor. Los campos producidos por un inductor espiral penetran en el sustrato, y como el plano de tierra se ubica a corta distancia, las corrientes parásitas en el plano de tierra reducen la inductancia que de otro modo se obtendría. La corriente parásita en el conductor de tierra gira en una dirección opuesta a la de la corriente en la espiral misma. Como resultado, el flujo del inductor de imagen en el suelo está en la dirección opuesta a la producida por la propia espiral, con el consiguiente efecto de que se reduce la inductancia total efectiva. Al crear un patrón de conductor roto, la inductancia de tierra se elimina en gran medida ya que las corrientes parásitas no pueden fluir [5].
Todos los inductores tienen una pérdida resistiva apreciable de conductores, y para los inductores en sustratos semiconductores, la pérdida debida a las corrientes de sustrato inducidas es

Figura\(\PageIndex{3}\): Placa de circuito que muestra el uso de componentes de montaje en superficie: (a) resistencia de chip o condensador con terminales metálicos en los dos extremos; (b) placa de circuito de microcinta RF poblada de un oscilador\(5\text{ GHz}\) controlado por voltaje [7] (los componentes más grandes tienen dimensiones\(1.6\text{ mm}\times 0.8\text{ mm}\)); y (c) identificación de varios componentes incluyendo una pila de varactores con cuatro diodos varactores y una barra de cortocircuito que es una\(0\:\Omega\) resistencia.
importante y a menudo domina. La pérdida en el sustrato es particularmente grande en los sustratos de silicio debido a la conductividad finita del sustrato y al flujo de corriente resultante. Estas corrientes inducidas siguen una trayectoria bajo los conductores de la espiral y, al igual que con las corrientes parásitas del plano de tierra, disminuye la inductancia lograda. Sin embargo, la resistencia de las líneas no ha cambiado. Por lo tanto, sobre el silicio es difícil lograr muy alto\(Q_{s}\) (la relación de energía almacenada a energía disipada por ciclo).
Los inductores agrupados se basan en bobinas de conductor, y hay capacitancia parásita entre los devanados [6]. Como resultado habrá una frecuencia donde la capacitancia y la inductancia resuenan a lo que se llama la frecuencia autorresonante. La impedancia de un inductor realista se muestra en la Figura\(\PageIndex{2}\) (c). Si el inductor práctico fuera puramente inductivo, entonces su impedancia aumentaría linealmente con la frecuencia. Sin embargo, debido a la resonancia, la inductancia efectiva aumenta justo antes de la resonancia haciendo que la impedancia del inductor práctico aumente más rápidamente que linealmente. Esto se ve en la Figura\(\PageIndex{2}\) (c), y este efecto se suele utilizar en circuitos de microondas de banda estrecha.

