6.7: Coincidencia de Impedancia Usando Gráficos Smith
- Page ID
- 80774
Las redes de coincidencia de elementos agrupados presentadas hasta ahora también se pueden desarrollar utilizando gráficos Smith que proporcionan un enfoque bastante intuitivo para el diseño de redes. Con la experiencia se encontrará que este es el enfoque preferido para desarrollar diseños, ya que las compensaciones pueden capturarse gráficamente. El diseño basado en gráficos de Smith se presentará usando ejemplos.
6.7.1 Coincidencia de dos elementos
Los ejemplos aquí se basan en los anteriores diseños de redes coincidentes de elementos agrupados que ahora utilizan la tabla Smith introducida en el Capítulo 3. Las regiones capacitivas e inductivas en el gráfico Smith se muestran en la Figura\(\PageIndex{1}\). En los ejemplos de diseño aquí presentados, se siguen círculos de resistencia constante o conductancia constante y estos corresponden a una reactancia o susceptancia variable, respectivamente.
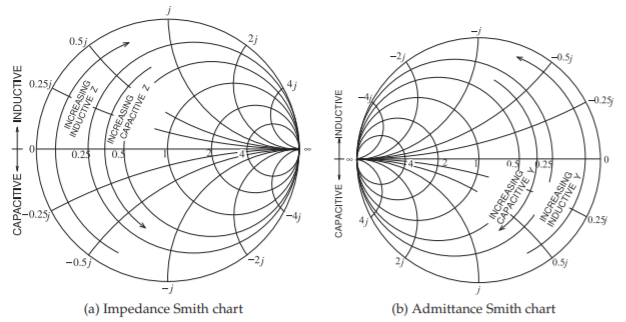
Figura\(\PageIndex{1}\): Regiones inductivas y capacitivas en gráficos Smith. El aumento de la impedancia capacitiva\((Z)\) indica una capacitancia menor; el aumento de la admitancia inductiva\((Y)\) indica menor inductancia.
Ejemplo\(\PageIndex{1}\): Two-Element Matching Network Design Using a Smith Chart
Desarrollar una red coincidente de dos elementos para hacer coincidir una fuente con una impedancia de\(R_{S} = 25\:\Omega\) a una carga\(R_{L} = 200\:\Omega\) (ver Figura\(\PageIndex{2}\)).
Solución
El objetivo del diseño es presentar impedancias conjugadas coincidentes con la fuente y la carga. Sin embargo, dado que aquí las impedancias de fuente y carga son reales, el objetivo del diseño es\(Z_{1} = R_{S}\) y\(Z_{2} = R_{L}\). Las resistencias de carga y fuente se representan en el gráfico Smith en la Figura\(\PageIndex{4}\) (a) después de elegir una impedancia de normalización de\(Z_{0} = 50\:\Omega\) (y así\(r_{S} = R_{S}/Z_{0} = 0.5\) y\(r_{L} = R_{L}/Z_{0} = 4\)). La impedancia normalizada de la fuente\(r_{S}\), es Punto\(\mathsf{A}\), y la impedancia de carga normalizada\(r_{L}\),, es Punto\(\mathsf{C}\). La red coincidente debe ser sin pérdidas, lo que significa que el diseño debe seguir líneas de resistencia constante (en la parte de impedancia de la carta Smith) o conductancia constante (en la parte de admitancia del gráfico Smith). Entonces Puntos\(\mathsf{A}\) y\(\mathsf{C}\) deben estar en los círculos anteriores y los círculos deben cruzarse si es posible un diseño. El diseño se puede ver como retroceder desde la fuente hacia la carga o retroceder desde la carga hacia la fuente. (Las vistas dan como resultado diseños idénticos.) Aquí la vista tomada es retroceder desde la fuente hacia la carga.
Un posible diseño se muestra en la Figura\(\PageIndex{4}\) (a). Desde Punto\(\mathsf{A}\), se sigue la línea de resistencia constante hasta el Punto\(\mathsf{B}\) (hay una reactancia en serie creciente a lo largo de esta trayectoria). Desde Punto\(\mathsf{B}\), el locus sigue una línea de conductancia constante hasta el punto final, Punto\(\mathsf{C}\). También existe un diseño alternativo que sigue la trayectoria mostrada en la Figura\(\PageIndex{4}\) (b). Solo hay dos diseños que tienen un camino desde\(\mathsf{A}\) hasta\(\mathsf{B}\) seguir solo dos arcos. En este punto se han perfilado dos diseños. El siguiente paso es asignar valores de elementos.
El diseño mostrado en la Figura\(\PageIndex{4}\) (a) comienza con\(r_{S}\) seguido de una reactancia en serie\(x_{S}\), tomando el locus de\(\mathsf{A}\) a\(\mathsf{B}\). Luego una susceptancia capacitiva de derivación,\(b_{P}\), toma el locus de\(\mathsf{B}\) a\(\mathsf{C}\) y\(r_{L}\). En Punto\(\mathsf{A}\) la reactancia\(x_{A} = 0\), en Punto\(\mathsf{B}\) la reactancia\(x_{B} = 1.323\). Este valor se lee en el gráfico de Smith, requiriendo que un arco como se muestra sea interpolado entre los arcos proporcionados. Cabe señalar que no todas las versiones de los gráficos de Smith incluyen signos negativos, ya que el gráfico se vuelve demasiado complicado. Por lo tanto, el usuario necesita estar al tanto y agregar señales en su caso. La reactancia en serie normalizada es
\[\label{eq:1}x_{S}=x_{B}-x_{A}=1.323-0=1.323 \]
es decir,
\[\label{eq:2}X_{S}=x_{s}Z_{0}=1.323\times 50=66.1\:\Omega \]
Un elemento capacitivo de derivación toma el lugar de punto\(\mathsf{B}\) a punto\(\mathsf{C}\) y
\[\label{eq:3}b_{P}=b_{C}-b_{B}=0-(-0.661)=0.661 \]
por lo
\[\label{eq:4}B_{P}-b_{P}/Z_{0}=0.661/50=13.22\text{ mS}\quad\text{or}\quad X_{P}=-1/B_{P}=-75.6\:\Omega \]
El diseño final se muestra en la Figura\(\PageIndex{3}\).
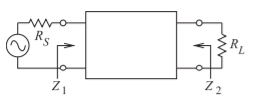
Figura\(\PageIndex{2}\): Objetivos de diseño para Ejemplo\(\PageIndex{1}\). \(R_{S} = 25\:\Omega,\: R_{L} = 200\:\Omega\).
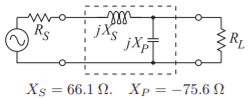
Figura\(\PageIndex{3}\): Diseño final para Ejemplo\(\PageIndex{1}\) usando la ruta que se muestra en la Figura\(\PageIndex{4}\) (a).
Figura\(\PageIndex{4}\): Diseños alternativos para Ejemplo\(\PageIndex{1}\). La impedancia de normalización es\(50\:\Omega\).
Una de las ventajas de utilizar el gráfico Smith es que el diseño avanza por etapas, con la estructura del diseño desarrollada antes de que se calculen los valores numéricos reales. Por supuesto, es difícil extraer valores precisos de un gráfico, por lo que los diseños se desbastan regularmente en un gráfico de Smith y se refinan con herramientas CAD. Ejemplo\(\PageIndex{1}\) emparejó una fuente resistiva con una carga resistiva. El siguiente ejemplo considera la coincidencia de impedancias complejas de carga y fuente. En el enfoque algorítmico anterior para hacer coincidir el diseño de redes, la absorción y la resonancia se introdujeron como estrategias para tratar terminaciones complejas. El diseño no siempre fue sencillo. Se verá que esta complicación desaparece con un diseño basado en gráficos de Smith, ya que conceptualmente no es muy diferente del problema resistivo del Ejemplo\(\PageIndex{1}\).
Ejemplo\(\PageIndex{2}\): Matching Network Design With Complex Impedances
Desarrollar una red coincidente de dos elementos para hacer coincidir una fuente con una impedancia de\(Z_{S} = 12.5 + 12.5\jmath\:\Omega\) a una carga\(Z_{L} = 50 − 50\jmath\:\Omega\), como se muestra en la Figura\(\PageIndex{5}\).
Solución
El objetivo del diseño es presentar impedancias conjugadas coincidentes a la fuente y carga; es decir,\(Z_{1} = Z_{S}^{\ast}\) y\(Z_{2} = Z_{L}^{\ast}\). La elección aquí es diseñar para\(Z_{1}\); es decir, los elementos se insertarán frente\(Z_{L}\) a para producir la impedancia\(Z_{1}\). Las impedancias normalizadas de fuente y carga se representan en la Figura\(\PageIndex{6}\) (a) usando una impedancia de normalización de\(Z_{0} = 50\:\Omega\), so\(z_{S} = Z_{S}/Z_{0} = 0.25 + 0.25\jmath\) (Punto\(\mathsf{S}\)) y\(z_{L} = Z_{L}/Z_{0} = 1 −\jmath\) (Punto\(\mathsf{C}\)).
La impedancia a sintetizar es\(z_{1} = Z_{1}/Z_{0} = z_{S}^{\ast} = 0.25− 0.25\jmath\) (Punto\(\mathsf{A}\)). La red coincidente debe ser sin pérdidas, lo que significa que el diseño de elementos grumados debe seguir líneas de resistencia constante (en la parte de impedancia del gráfico Smith) o conductancia constante (en la parte de admitancia del gráfico Smith). Puntos\(\mathsf{A}\) y\(\mathsf{C}\) deben estar en los círculos anteriores y los círculos deben cruzarse si es posible un diseño.
El diseño se puede ver como retroceder desde la impedancia de carga hacia el conjugado de la impedancia de la fuente. La dirección del locus de impedancia es importante. Un posible diseño se muestra en la Figura\(\PageIndex{6}\) (a). Desde\(\mathsf{C}\) el punto se sigue la línea de conductancia constante hasta el punto\(\mathsf{B}\) (hay una susceptancia de derivación positiva creciente [es decir, capacitiva] a lo largo de esta trayectoria). Desde Punto\(\mathsf{B}\) el locus sigue una línea de resistencia constante al punto final, Punto\(\mathsf{A}\).
El diseño mostrado en la Figura\(\PageIndex{6}\) (a) comienza con una susceptancia de derivación\(b_{P}\), tomando el locus de Punto\(\mathsf{C}\) a Punto\(\mathsf{B}\) y luego una reactancia inductiva en serie\(x_{S}\), llevando el locus a Punto\(\mathsf{A}\). En\(\mathsf{C}\) el Punto la susceptancia\(b_{C} = 0.5\), en\(\mathsf{B}\) el Punto la susceptancia\(b_{B} = 1.323\). Este valor se lee en el gráfico de Smith, requiriendo que un arco de susceptancia constante, como se muestra, sea interpolado entre los arcos de susceptancia constante proporcionados. La susceptancia de derivación normalizada es
\[\label{eq:5}b_{P}=b_{B}-b_{C}=1.323-0.5=0.823 \]
es decir,
\[\label{eq:6}B_{P}=b_{P}/Z_{0}=0.823/(50\:\Omega)=16.5\text{ mS or }X_{P}=-1/B_{P}=-60.8\:\Omega \]
Un elemento reactivo en serie toma el lugar de punto\(\mathsf{B}\) a punto\(\mathsf{A}\), por lo que
\[\label{eq:7}x_{S}=x_{A}-x_{B}=-0.25-(0.661)=0.411 \]
por lo
\[\label{eq:8}X_{S}=x_{S}Z_{0}=0.411\times 50\:\Omega =20.6\:\Omega \]
El diseño final se muestra en la Figura\(\PageIndex{7}\).
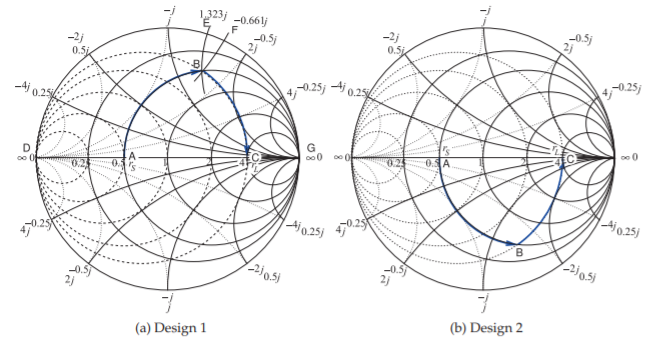
Solo hay dos diseños que tienen una trayectoria de Punto\(\mathsf{C}\) a Punto\(\mathsf{A}\) siguiendo solo dos arcos. En Diseño\(1\), que se muestra en la Figura\(\PageIndex{6}\) (a), la Ruta\(\mathsf{CBA}\) es mucho más corta que la Trayectoria\(\mathsf{CHA}\) para Diseño\(2\) mostrada en la Figura\(\PageIndex{6}\) (b). La longitud de la ruta es una indicación aproximada de la reactancia total requerida, y cuanto mayor sea la reactancia, mayor será el almacenamiento de energía y, por lo tanto, más estrecho es el ancho de banda del diseño. (El ancho de banda relativo real depende de los niveles de voltaje y corriente en la red; sin embargo, los criterios de longitud de ruta son una regla general importante). Por lo tanto, se\(1\) puede esperar que el Diseño tenga un ancho de banda mucho mayor que el Diseño\(2\) Dado que el diseño de ancho de banda más amplio suele ser un objetivo, generalmente es preferible un diseño que requiera una ruta más corta en un gráfico de Smith.
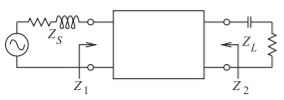
Figura\(\PageIndex{5}\): Objetivos de diseño para Ejemplo\(\PageIndex{2}\).
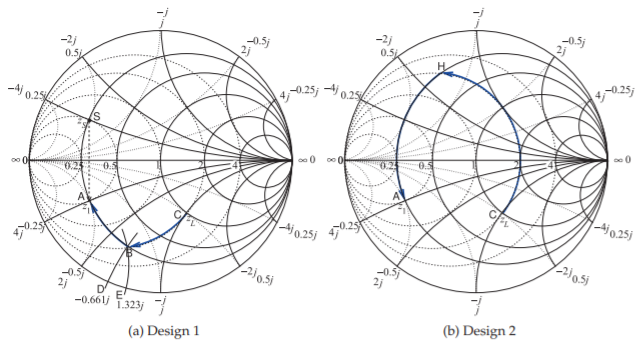
Figura\(\PageIndex{6}\): Diseños basados en gráficos de Smith utilizados en Ejemplo\(\PageIndex{2}\). (\(50\:\Omega\)normalización utilizada.)
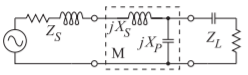
Figura\(\PageIndex{7}\): Circuito final para Diseño\(1\) de Ejemplo\(\PageIndex{2}\). \(X_{S} = 20.6\:\Omega,\: X_{P} = −60.8\:\Omega\).

