6.8: Coincidencia distribuida
- Page ID
- 80759
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)El emparejamiento mediante elementos agrupados conduce a elementos agrupados en serie y derivación. Los elementos de derivación se pueden implementar usando líneas de transmisión de derivación, ya que una longitud corta (menos de un cuarto de longitud de onda) de línea de transmisión cortocircuitada parece un inductor y una sección corta de línea de transmisión de circuito abierto parece un condensador. Sin embargo, en la mayoría de las tecnologías de líneas de transmisión no es posible realizar los elementos en serie como longitudes de líneas de transmisión. Si bien se ha demostrado que una longitud corta de la línea de transmisión es inductiva, reemplazar los inductores en serie por una longitud de línea de transmisión de alta impedancia característica no es el mejor enfoque para realizar redes. La solución es utilizar longitudes de línea de transmisión junto con elementos de derivación. Si el espacio no está en una prima, esta es una solución óptima, ya que las líneas de transmisión tienen una pérdida mucho menor que un inductor agrupado. Las líneas de transmisión en serie giran el coeficiente de reflexión en el gráfico de Smith.
Al igual que con todos los diseños coincidentes, el uso de líneas de transmisión comienza con una topología en mente. Varias topologías se muestran en la Figura\(\PageIndex{1}\). La figura\(\PageIndex{1}\) (a) es la
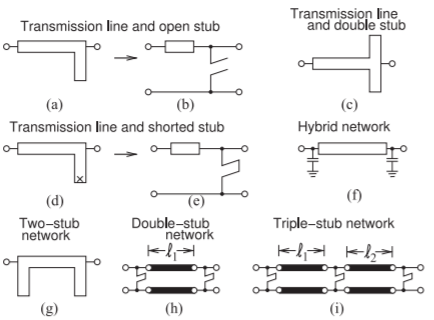
Figura\(\PageIndex{1}\): Redes coincidentes con elementos de línea de transmisión.
vista superior de una red de coincidencia de microcinta con una línea de transmisión en serie y un trozo realizado como una línea de transmisión de circuito abierto. La figura\(\PageIndex{1}\) (b) es un esquema abreviado para este circuito. Hacer coincidir el diseño de la red se convierte entonces en un problema para elegir las longitudes e impedancias características de las líneas. El trozo aquí se utiliza para realizar un elemento de derivación capacitiva. Esta red corresponde a la coincidencia de dos elementos con un condensador de derivación. El valor de la capacitancia de derivación se puede aumentar usando un stub dual, como se muestra en la Figura\(\PageIndex{1}\) (c), donde las impedancias de entrada capacitiva de cada stub están en paralelo. El circuito dual al de la Figura\(\PageIndex{1}\) (a) se muestra en la Figura\(\PageIndex{1}\) (d) junto con su representación esquemática en la Figura\(\PageIndex{1}\) (e). Este circuito tiene un trozo cortocircuitado que realiza una inductancia de derivación.
La mezcla de condensadores agrupados con un elemento de línea de transmisión, como se muestra en la Figura\(\PageIndex{1}\) (f), realiza un diseño de red mucho más eficiente en el espacio. Hay muchas variaciones en el diseño de redes coincidentes basado en stubs, incluido el diseño de dos stub en la Figura\(\PageIndex{1}\) (g).
Una situación común que se encuentra en el laboratorio es el emparejamiento de circuitos que están en desarrollo. Los elementos de laboratorio disponibles para emparejar incluyen el afinador de talón, que se muestra en la Figura\(\PageIndex{2}\) (a), y el afinador de doble trozo, que se muestra en la Figura\(\PageIndex{2}\) (b). Con el sintonizador de doble talón la longitud de la línea de transmisión en serie es fija, pero los stubs pueden tener longitud variable usando longitudes de líneas de transmisión con cortocircuitos deslizantes. Sin embargo, no todas las impedancias se pueden igualar usando un sintonizador de doble trozo. Un sintonizador de triple talón puede coincidir con todas las impedancias que se le presentan [2]. El sintonizador de doble slug mostrado en la Figura\(\PageIndex{2}\) (c) tiene babosas dieléctricas, cada una de las cuales introduce una sección corta de línea de menor impedancia. Los slugs se mueven hacia arriba y hacia abajo de la línea y evitan los cambios rápidos en las impedancias que ocurren con los sintonizadores stub y como resultado el sintonizador de doble slug proporciona una coincidencia de ancho de banda más amplia que el sintonizador de doble stub. El sintonizador de babosas de tornillo deslizante que se muestra en la Figura\(\PageIndex{2}\) (d) puede lograr una coincidencia de banda ancha. Aquí se puede bajar una pieza metálica en la línea de losa cambiando la impedancia de una sección de la línea de transmisión y afecta principalmente a la magnitud del coeficiente de reflexión mientras que mover la pieza metálica a lo largo de la línea afecta principalmente a la fase. Este es el tipo de sintonizador incorporado en sintonizadores automatizados controlados por computadora.
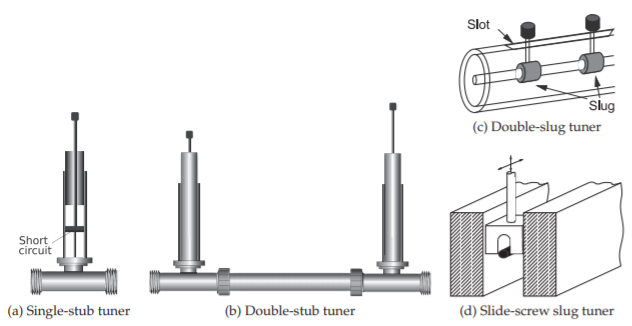
Figura\(\PageIndex{2}\): Sintonizadores de laboratorio.
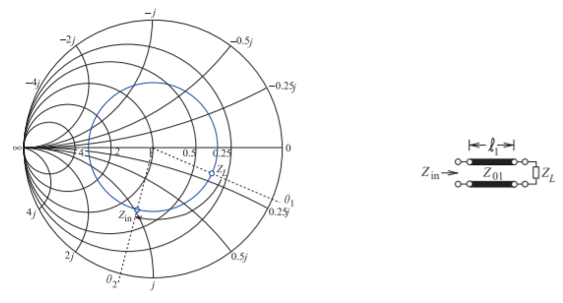
Figura\(\PageIndex{3}\): Rotación de la impedancia de entrada de una línea de transmisión en una gráfica Smith normalizada a\(Z_{01}\) medida que aumenta la longitud de la línea.
6.8.1 Coincidencia de talón
En esta sección se considerará la coincidencia usando una línea de transmisión en serie y un trozo. Esto corresponde a las topologías de circuito microstrip mostradas en las figuras\(\PageIndex{1}\) (a y d). Primero, considere la línea de transmisión terminada que se muestra en la Figura\(\PageIndex{3}\). Cuando la longitud,\(\ell_{1}\), de la línea es cero, la impedancia de entrada de la línea,\(Z_{\text{in}}\), es igual\(Z_{L}\). La mejor manera de cambiar se describe considerando el coeficiente de reflexión de entrada,\(\Gamma_{\text{in}}\), de la línea. Si el coeficiente de reflexión se normaliza a\(Z_{01}\), entonces la magnitud de\(\Gamma_{\text{in}}\) y su fase varía como el doble de la longitud eléctrica de la línea. Esta situación se muestra en la gráfica de Smith en la Figura\(\PageIndex{3}\), donde\(Z_{L}\) se elige arbitrariamente. El coeficiente de reflexión de entrada de
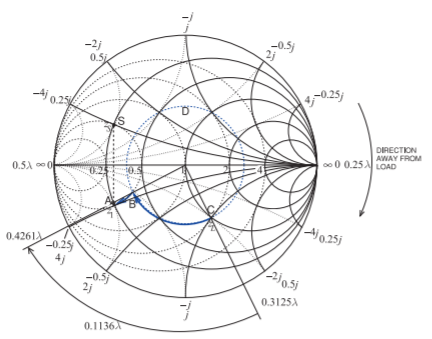
Figura\(\PageIndex{4}\): Diseño por ejemplo\(\PageIndex{1}\).
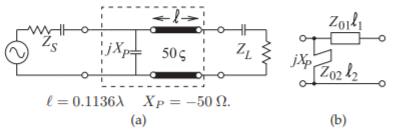
Figura\(\PageIndex{5}\): Diseño de red coincidente de un solo trozo del Ejemplo\(\PageIndex{1}\): (a) diseño eléctrico; y (b) diseño eléctrico con un trozo de derivación.
la línea gira en el sentido de las agujas del reloj a medida que aumenta la longitud de la línea. Una forma de recordar esto es considerar una línea de circuito abierto. Cuando la longitud de la línea es cero,\(Y_{\text{in}} = 0\) y\(\Gamma_{\text{in}} = +1\). Una longitud corta de esta línea es capacitiva de manera que su coeficiente de reflexión estará en la mitad inferior del gráfico de Smith. Se puede usar una longitud de línea para rotar la impedancia a un punto apropiado para seguir una línea de conductancia constante a la impedancia de entrada deseada.
Ejemplo\(\PageIndex{1}\): Matching Network Design With a Transmission Line and a Single Stub
Diseñe una red coincidente de dos elementos para hacer coincidir una fuente con una impedancia\(Z_{S} = 12.5 + 12.5\jmath\:\Omega\) a una carga\(Z_{L} = 50 − 50\jmath\:\Omega\), como se muestra en la Figura 6.7.5. Este ejemplo repite el diseño del Ejemplo 6.7.2, pero ahora usando una línea de transmisión.
Solución
Al igual que en el Ejemplo 6.7.2, elija\(Z_{0} = 50\:\Omega\) y la ruta de diseño es de\(z_{L} = Z_{L}/Z_{0} = 1−\jmath\) a\(z_{s}^{\ast}\), donde\(z_{s} = 0.25 + 0.25\jmath\). Una posible solución de diseño se indica en la Figura\(\PageIndex{4}\). La longitud de línea,\(\ell\) (tomando el locus de Punto\(\mathsf{C}\) a Punto\(\mathsf{B}\)), es
\[\ell=0.4261\lambda -0.3125\lambda =0.1136\lambda\nonumber \]
y la susceptancia de derivación normalizada,\(b_{P}\) (tomando el locus de Punto\(\mathsf{B}\) a Punto\(\mathsf{C}\)), es
\[b_{P}=b_{A}-b_{B}=2-1=1 \nonumber \]
Así\(X_{P} = (−1/b_{P} )\times 50\:\Omega = −50\:\Omega\). El diseño final se muestra en la Figura\(\PageIndex{5}\) (a). El diseño del talón de la Figura\(\PageIndex{5}\) (b) sigue el procedimiento descrito en el Ejemplo 6.5.1.
6.8.2 Emparejamiento Híbrido Distribuido Lumped-
Una red de adaptación sin pérdidas puede tener líneas de transmisión, así como inductores y capacitores. Si la impedancia de referencia o normalización del sistema es la impedancia característica de una línea de transmisión, entonces el lugar de la impedancia de entrada (o coeficiente de reflexión) de la línea con respecto a la longitud de la línea es un arco en un círculo centrado en el origen de la gráfica Smith. La dirección del arco es en el sentido de las agujas del reloj a medida que la longitud eléctrica de la línea se aleja de la carga. Entonces es posible una red híbrida coincidente que combine una longitud de línea de transmisión con un elemento agrupado (preferiblemente un condensador en lugar de un inductor ya que el inductor tendría un relativamente menor\(Q\)).

