2.13: Identidades de red de Kuroda y Norton
- Page ID
- 85166
Las identidades de red de Kuroda y Norton son varios pares de redes equivalentes que facilitan la transformación de un prototipo a otro, particularmente transformaciones que permiten implementaciones de líneas de transmisión realizables.
2.13.1 Identidades de Kuroda
Las identidades de Kuroda encarnan una serie de manipulaciones específicas usando inversores de impedancia o admitancia. Son particularmente útiles para implementar las transformaciones de Richards, ya que separan físicamente los stubs de línea de transmisión, transforman los stubs de serie en stubs de derivación y pueden cambiar impedancias características que son demasiado pequeñas o demasiado altas a valores prácticamente realizables. Las identidades de Kuroda son una serie de redes equivalentes de dos puertos, como se muestra en la Figura\(\PageIndex{1}\). La prueba se deriva obteniendo los\(ABCD\) parámetros de los dos puertos similares a la técnica utilizada a lo largo de este capítulo. Las identidades mostradas en la Figura\(\PageIndex{1}\) son de banda estrecha. Con talones que reemplazan a los elementos agrupados, las identidades de Kuroda tienen entonces anchos de banda más amplios. Las identidades de Kuroda con talones se muestran en la Figura\(\PageIndex{2}\). El uso principal de estas identidades es transformar diseños con stubs de serie (además de posibles stubs de derivación) en diseños con shunt
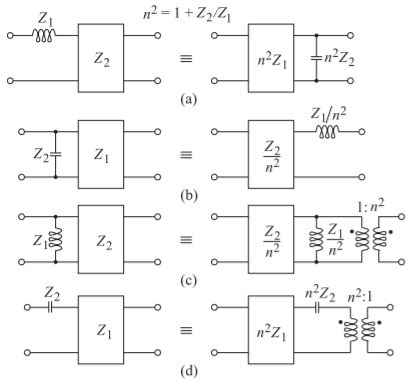
Figura\(\PageIndex{1}\): Identidades de Kuroda. Aquí los inversores son inversores de impedancia y la designación se refiere a la impedancia del inversor. Recordemos que un inversor de impedancia\(Z_{1}\) puede ser realizado por una línea de transmisión larga de un cuarto de longitud de onda de impedancia característica\(Z_{1}\). (Como es habitual, se indican las impedancias de los elementos).
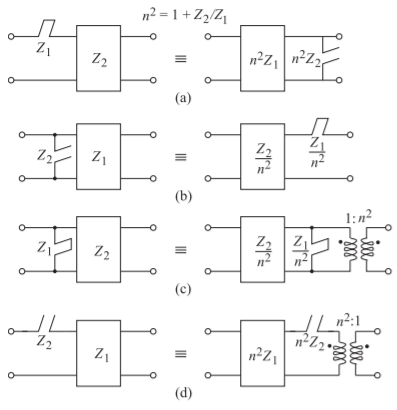
Figura\(\PageIndex{2}\): La forma stub de las identidades de Kuroda con inversores de impedancia. Las impedancias de stub mostradas son las impedancias de entrada de los stubs.
sólo talones.
Para ver cómo se utilizan estas identidades, considere la identidad que se muestra en la Figura\(\PageIndex{1}\) (a). La red de la izquierda tiene un inductor en serie que, utilizando líneas de transmisión, se realiza mediante un stub serie. Un stub de serie no se puede realizar en la mayoría de las tecnologías de línea de transmisión, incluyendo microstrip. Usando la identidad que se muestra a la derecha en la Figura\(\PageIndex{1}\) (a), el stub en serie se reemplaza por el stub de derivación utilizado para realizar el condensador de derivación. Al mismo tiempo, escalado de impedancia
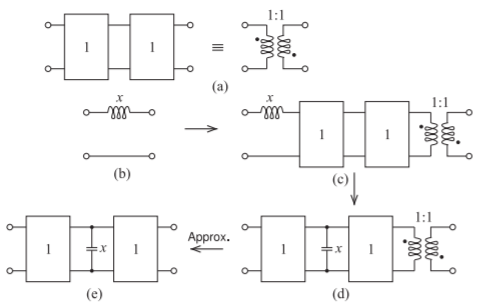
Figura\(\PageIndex{3}\): Transformación de un inductor en serie en un condensador de derivación entre inversores.
puede ser utilizado. Si la impedancia del inversor en la red de la izquierda es demasiado baja, entonces se puede escalar por un factor\(n^{2}\), donde\(n^{2} =1+ Z_{2}/Z_{1}\).
Un uso de las transformaciones de Kuroda es convertir un inductor en serie en un condensador de derivación. Considere la transformación del inductor que se muestra en la Figura\(\PageIndex{3}\). La Figura\(\PageIndex{3}\) (a) muestra que dos inversores en cascada son eléctricamente equivalentes a un transformador inversor. Dado que cada inversor es un inversor unitario (ya sea un inversor de\(1\:\Omega\) impedancia o un inversor de\(1\text{ S}\) admitancia), la equivalencia es un transformador inversor unitario que corresponde a un cambio de\(180^{\circ}\) fase. Entonces, la transformación de un inductor en serie comienza con la transformación del inductor (con valor\(x\)) en la Figura\(\PageIndex{3}\) (b) en la red de la Figura\(\PageIndex{3}\) (c) en la que la cascada del inversor y el transformador inversor se cancelan entre sí. Usando la identidad de Kuroda en la Figura\(\PageIndex{2}\) (a), la red en la Figura\(\PageIndex{3}\) (c) se convierte en la red eléctricamente idéntica en la Figura\(\PageIndex{3}\) (d). Dado que la\(180^{\circ}\) rotación generalmente no importa en los circuitos, la transformación final que se muestra en la Figura\(\PageIndex{3}\) (e) suele ser aceptable. (La rotación solo importaría si hubiera otra ruta entre la entrada y la salida, ya que entonces la fase afectaría la forma en que las señales en múltiples trayectorias combinadas). Ahora el condensador en la Figura\(\PageIndex{3}\) (e) tiene el valor numérico\(x\), el mismo que el valor numérico del inductor original. Esto es resultado del uso de inversores unitarios. El resultado clave aquí es que un inductor en serie es equivalente a un condensador de derivación flanqueado por dos inversores.
2.13.2 Identidades de Norton
Las transformaciones de Norton permiten escalar la magnitud de los valores de elementos agrupados [16, 17]. Las transformaciones de Norton se muestran en la Figura\(\PageIndex{4}\) donde\(K\) está el factor de escalado. Se introducen elementos adicionales en estas transformaciones, incluyendo elementos posiblemente valorados negativamente. Generalmente estos elementos se pueden combinar con otros elementos para que los elementos a realizar sean positivos (por ejemplo, condensador positivo) y el transformador también se pueda reemplazar a través de transformaciones posteriores utilizando, por ejemplo, las identidades de Kuroda.
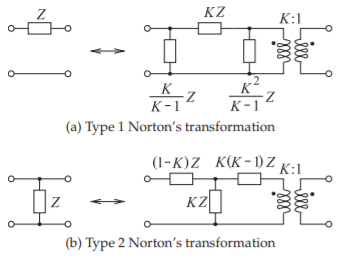
Figura\(\PageIndex{4}\): Transformaciones de Norton.

