2.12: La transformación de Richards
- Page ID
- 85192
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)La transformación de Richards es un esquema notable que toma en cuenta las propiedades reales de las líneas de transmisión, dando lugar a implementaciones basadas en líneas de transmisión de banda ancha de prototipos de filtro de elementos agrupados [12, 13, 14, 15].
2.12.1 Líneas de Transformación y Transmisión de Richard
Considere una sección de línea de transmisión de longitud eléctrica\(\theta\) con\(ABCD\) parámetros
\[\label{eq:1}T=\left[\begin{array}{cc}{\cos(\theta)}&{\jmath Z_{0}\sin(\theta)}\\{\jmath /Z_{0}\sin(\theta)}&{\cos (\theta)}\end{array}\right] \]
Si esta línea termina en una carga\(Z_{L}\), entonces su impedancia de entrada es
\[\label{eq:2}Z_{\text{in}}(\theta)=\frac{\cos(\theta)Z_{L}+\jmath Z_{0}\sin(\theta)}{\jmath /Z_{0}\sin(\theta)Z_{L}+\cos(\theta)} \]
Ahora examina dos condiciones extremas. A medida que aumenta la impedancia de carga, convirtiéndose eventualmente en un circuito abierto, la impedancia de entrada de una línea con longitud eléctrica\(\theta\) se define en términos de una cotangente de la longitud eléctrica:
\[\begin{align}\label{eq:3}Z_{L}\to\infty\quad \Rightarrow Z_{\text{in}}(\theta)&=\frac{Z_{0}}{\jmath}\cot(\theta) \\ \label{eq:4}Y_{\text{in}}(\theta)&=\jmath Y_{0}\tan(\theta)\end{align} \]
A medida que la impedancia de carga se reduce para convertirse en un cortocircuito, la impedancia de entrada de una línea con longitud eléctrica\(\theta\) se define en términos de una tangente de la longitud eléctrica:
\[\label{eq:5}Z_{L}\to 0\quad\Rightarrow\quad Z_{\text{in}}(\theta)=\jmath Z_{0}\tan(\theta) \]
Estos resultados conducen a la transformación de Richards, que sustituye a la variable Laplace,\(s\), por la variable de Richards,\(S\), donde\(S =\jmath\alpha\tan(\theta)\). Esta transformación está escrita
\[\label{eq:6}s\to S=\jmath\alpha\tan(\theta) \]
Por ahora\(\alpha\) y\(\theta\) son constantes que se pueden elegir como variables de diseño. \(\theta\), por supuesto, es la longitud eléctrica de la línea. Además,\(\alpha\) debe tener las unidades de impedancia y es la impedancia característica de la línea de transmisión.
Aplicando la transformación de Richards a un condensador, la admitancia del elemento se transforma de la siguiente manera:
\[\label{eq:7}y=sC\to Y=SC=\jmath\alpha C\tan(\theta) \]
para que el condensador se transforme en un trozo de circuito abierto con admitancia característica
\[\label{eq:8}Y_{0}=\alpha C \]
Si se va a realizar un condensador de elemento grumo con admitancia\(y = sC\) usando una línea de transmisión, la admitancia\(Y = SC =\jmath\alpha C \tan(\theta )\) se realiza en su lugar. Hay dos parámetros a seleccionar para realizar esta admisión. El primero,\(\alpha\), es la admitancia característica de la línea de transmisión (y para cualquier topología de línea de transmisión dada existe una admitancia o impedancia característica mínima y máxima que se pueda realizar), y\(\theta\) es la longitud eléctrica de la línea.
Aplicando la transformación a un inductor, la impedancia del elemento se transforma de la siguiente manera:
\[\label{eq:9}Z=sL\to Z=SL=\jmath\alpha L\tan(\theta) \]
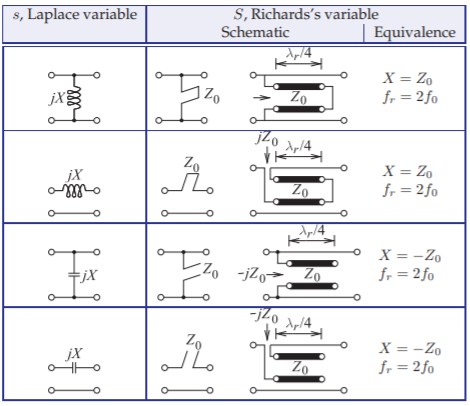
Figura\(\PageIndex{1}\): Equivalencias resultantes de la transformación de Richards. Con\(f_{r} = 2f_{0}\) la línea de transmisión, los talones son de un octavo de longitud de onda en\(f_{0}\).
para que el inductor se transforme en un trozo cortocircuitado con impedancia característica
\[\label{eq:10}Z_{0}=\alpha L \]
Así, la transformada de Richards convierte un inductor en un trozo cortocircuitado y un condensador en un trozo de circuito abierto.
2.12.2 La transformación y los talones de Richard
Existe una dualidad entre los stubs y los inductores y capacitores; están acoplados por la transformación de Richards. Una de las cantidades importantes utilizadas en la transformación es la frecuencia proporcional\(f_{r}\), que con mayor frecuencia se elige como el doble de la frecuencia de operación,\(f_{0}\). Teniendo en cuenta los talones que tienen un cuarto de longitud de onda\(f_{r}\), la dualidad es como se muestra en la Figura\(\PageIndex{1}\).
2.13.3 La transformación de Richard aplicada a un filtro de paso bajo
En esta sección, la transformación de Richards se utiliza para realizar un filtro de elementos grumosos en forma distribuida. El ejemplo de diseño comienza considerando un filtro paso bajo Chebyshev con la característica de transmisión
\[\label{eq:11}|T(s)|^{2}=\frac{1}{1+\varepsilon^{2}|K(s)|^{2}} \]
Con la transformación de Richards\((s\to\jmath\omega\to\jmath\alpha\tan (\theta))\) esto se convierte
\[\label{eq:12}|T(\jmath\alpha\tan\theta)|^{2}=\frac{1}{1+\varepsilon^{2}|K(\jmath\alpha\tan\theta))|^{2}} \]
Por lo tanto, el borde de banda de paso en\(\omega = 1\) se mapea\(\omega =\theta_{1}\) como
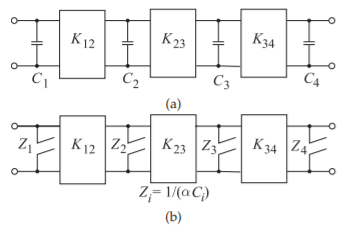
Figura\(\PageIndex{2}\): Prototipos de paso bajo: (a) prototipo de paso bajo como filtro de escalera con inversores; y (b) prototipo distribuido de paso bajo con stubs de circuito abierto (se indica la impedancia que mira al interior del stub).
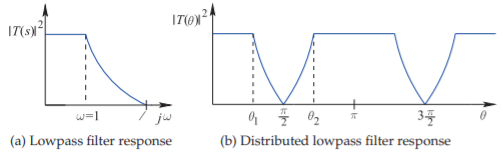
Figura\(\PageIndex{3}\): Transformación de paso bajo a paso bajo distribuido. \(s =\jmath\omega\).
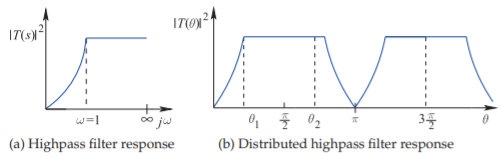
Figura\(\PageIndex{4}\): Transformación de paso alto a paso alto distribuido. \(s =\jmath\omega\).
\[\label{eq:13}\omega =1\to\alpha\tan (\theta_{1}) \]
para que
\[\label{eq:14}\alpha=\frac{1}{\tan(\theta_{1})} \]
Recordando que un condensador se transforma en un stub de circuito abierto (ver Ecuación\(\eqref{eq:8}\)), la transformación de Richards aplicada al prototipo de filtro de paso bajo da como resultado un filtro con elementos de línea de transmisión solamente, como se muestra en la Figura\(\PageIndex{2}\), siempre que los inversores se realicen usando transmisión líneas.
La implementación de un filtro de paso bajo en forma distribuida da como resultado bandas de paso y bandas de parada que se repiten en frecuencia, como se muestra en la Figura\(\PageIndex{3}\). Esto ocurre porque las líneas de transmisión se utilizan para realizar elementos agrupados y los parámetros de dos puertos de una línea de transmisión repiten cada longitud de onda (o media longitud de onda en algunos casos). Por ejemplo, la impedancia de entrada de un trozo es la misma ya sea de media longitud de onda o de una longitud de onda larga.
2.12.4 La transformación de Richard aplicada a un filtro de paso alto
Con referencia a la Figura\(\PageIndex{4}\) (a), el borde de banda de paso en\(\omega = 1\) se mapea\(\theta_{1}\), como se muestra en la Figura\(\PageIndex{4}\) (b). Esto significa que la banda de paso en\(\omega = 1\) está mapeada
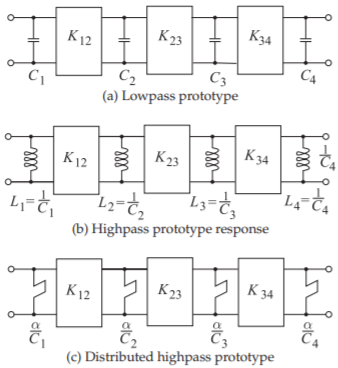
Figura\(\PageIndex{5}\): Transformación de prototipos en escalera. (Las impedancias de entrada de los stubs se indican en (c).)
a\(\theta_{1}\) as (tenga en cuenta que\(\theta_{1}\) es la longitud eléctrica en el borde de la banda)
\[\label{eq:15}\omega =1\to\alpha\tan(\theta_{1}) \]
para que
\[\label{eq:16}\alpha =\frac{1}{\tan(\theta_{1})} \]
La secuencia de pasos que transforma un prototipo de paso bajo agrupado en su prototipo de paso alto distribuido se muestra en la Figura\(\PageIndex{5}\). Como se discutió anteriormente, todos los inversores pueden aproximarse mediante líneas de transmisión de longitud\(\pi /2\) a la frecuencia de esquina del filtro.

