2.18: Respuesta transitoria de un filtro de paso de banda
- Page ID
- 85199
Figura\(\PageIndex{1}\): Filtro Chebyshev\(5\) de orden th-elemento terrado.
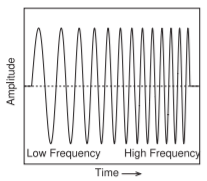
Figura\(\PageIndex{2}\): Un chirrido lineal.
Un filtro de paso de banda normalmente se caracteriza por su frecuencia central y ancho de banda, y las señales sinusoidales que están dentro del ancho de banda son transmitidas por el filtro y las que están fuera de la banda de paso son reflejadas por el filtro. Sin embargo, si la señal cambia de frecuencia rápidamente, la respuesta transitoria del filtro puede ser inesperada [32, 33].
La figura\(\PageIndex{1}\) es un filtro de quinto orden con cada par de resonadores de derivación acoplados por un resonador en serie. En respuesta a un pulso de RF (un pulso de RF que varía sinusoidalmente), el filtro pasa energía en banda cuando todos los resonadores han alcanzado el estado estacionario. Cuando se elimina el pulso de RF, los resonadores perderán energía y eventualmente las señales de RF en los resonadores desaparecerán. Habrá un tiempo finito para “cargar” y “descargar” los resonadores del filtro.
Una prueba clásica de la respuesta de RF sobre frecuencia es usar un chirp lineal de RF, como se muestra en la Figura\(\PageIndex{2}\). Con un chirrido lineal, la frecuencia de la señal en el pulso cambia linealmente y suavemente a lo largo del tiempo de una frecuencia a otra. La Figura\(\PageIndex{3}\) (a) presenta la respuesta transitoria a la salida de
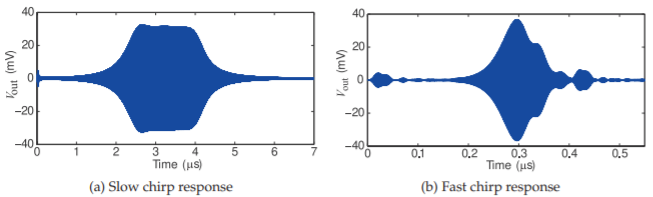
Figura\(\PageIndex{3}\): Respuesta transitoria de salida de un filtro Chebyshev de tercer orden con una frecuencia central de\(1\text{ GHz}\) y un\(30\text{ MHz}\) ancho de banda excitado por un chirp\(−20\text{ dBm}\) lineal de\(950\text{ MHz}\) a\(1050\text{ MHz}\): (a) tasa de chirp\(= 20\text{ MHz/}\mu\text{s}\), (b) tasa de chirp\(= 400\text{ MHz/}\mu\text{s}\). A la tasa de chirp más lenta, la respuesta del filtro es aproximadamente una superposición de respuestas de estado estacionario a medida que cambia la frecuencia (es decir, la respuesta es casi estacionaria). A la mayor tasa de chirp, la respuesta del filtro ya no se puede aproximar como una suma de respuestas de estado estacionario (es decir, ya no es cuasi-estacionaria). Después [34].
un\(1\text{ GHz}\) filtro\(30\text{ MHz}\) -ancho de banda excitado por un chirp lineal\(1\:\mu\text{s}\) -largo de\(950\text{ MHz}\) a\(1050\text{ MHz}\) con una tasa de chirp de\(20\text{ MHz/}\mu\text{s}\). Este es un chirrido relativamente lento. El chirp comienza en\(0\:\mu\text{s}\) y se detiene en\(5\:\mu\text{s}\). Por lo tanto, la frecuencia del chirp está dentro de banda en\(1.75\:\mu\text{s}\) y está fuera de banda en\(3.25\:\mu\text{s}\). El chirp es lo suficientemente lento como para que la respuesta de transmisión transitoria corresponda a la respuesta de frecuencia del filtro. Sin embargo, si el chirp es rápido, es posible que los resonadores no alcancen el estado estacionario, y entonces la respuesta transitoria del filtro no puede extrapolarse simplemente de su respuesta en el dominio de la frecuencia. Esto se ve en la Figura\(\PageIndex{3}\) (b), que es la respuesta del filtro a un chirp rápido con una tasa de chirp de\(400\text{ MHz/}\mu\text{s}\) y una duración de chirp de\(250\text{ ns}\), y comenzando en\(950\text{ MHz}\) y terminando en\(1050\text{ MHz}\). El chirrido de RF comienza fuera de banda en\(0\text{ ns}\), se convierte en banda en\(0.0875\:\mu\text{s}\), y vuelve a salir de banda\(0.1625\:\mu\text{s}\) antes de apagarse en\(0.25\:\mu\text{s}\). Curiosamente, hay una respuesta de salida casi inmediata, alrededor\(0.03\:\mu\text{s}\) cuando el chirrido de RF está fuera de banda. En general, la respuesta del filtro chirpeado no sigue la respuesta de frecuencia del filtro.
Otra visión del mismo fenómeno se examina para un filtro Chebyshev de\(7\) orden th-orden con una frecuencia central\(900\text{ GHz}\) y\(34\text{ MHz}\) ancho de banda de\(883\text{ MHz}\) a\(917\text{ MHz}\). La respuesta de transmisión en el dominio de frecuencia del filtro se muestra en la Figura\(\PageIndex{4}\). Las respuestas de transmisión a pulsos de RF\(0.25\:\mu\text{s}\) largos de diferentes frecuencias se muestran en la Figura\(\PageIndex{5}\). La frecuencia del pulso de RF se muestra en cada subparcela. La gráfica superior izquierda es la respuesta cuando el pulso de RF está en banda. Aquí el pulso de RF se aplica a\(0\:\mu\text{s}\) y se elimina en\(0.25\:\mu\text{s}\). Un retardo inicial en la respuesta de transmisión y lo que se conoce como una respuesta de cola larga se ve cuando se elimina el pulso de RF. Las otras gráficas en la Figura\(\PageIndex{5}\) muestran la respuesta del filtro ya que la RF se retrocede de la banda de paso. Entonces, incluso cuando la RF está fuera de banda, puede haber una salida apreciable del filtro al principio y al final del pulso de RF.
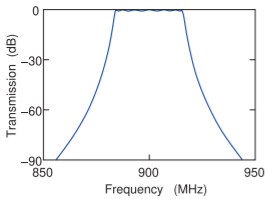
Figura\(\PageIndex{4}\): Respuesta de transmisión en el dominio de frecuencia de un filtro Chebyshev de\(7\) orden th-orden con una frecuencia central\(900\text{ GHz}\) y\(34\text{ MHz}\) ancho de banda de\(883\text{ MHz}\) a\(917\text{ MHz}\).
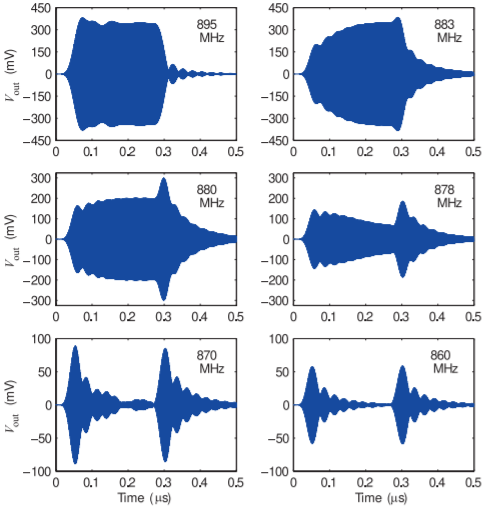
Figura\(\PageIndex{5}\): Respuesta transitoria a la salida del filtro de paso de banda Chebyshev de\(900\text{ MHz}\)\(7\) orden th-orden con una banda de paso de\(883\text{ MHz}\) a\(917\text{ MHz}\). La respuesta de frecuencia se muestra en la Figura\(\PageIndex{4}\). Después [34].

