2.17: Filtros activos

Con los circuitos activos, las pérdidas en los componentes de elementos grumados pueden ser compensadas por la ganancia de los dispositivos activos dando como resultado filtros con alto\(Q\). Los inversores también se pueden realizar de manera eficiente. El resultado neto es que los filtros activos proporcionan una ventaja de rendimiento por unidad de área sobre las realizaciones de elementos pasivos. Por supuesto, los filtros activos están limitados a señales de bajo nivel (como en los circuitos de recepción, y antes de las etapas del amplificador de potencia) ya que la potencia completa de la señal debe ser manejada por los dispositivos activos en el filtro activo. Con los dispositivos activos, se introduce ruido adicional y por lo tanto la cifra de ruido de un filtro activo debe considerarse en RF donde los anchos de banda son significativos.

A frecuencias de microondas los filtros activos basados en conceptos tradicionales de baja frecuencia tienen relativamente bajos\(Q\). Las aplicaciones de banda más alta\(Q\) y estrecha requieren inductores activos o técnicas distribuidas. Los filtros activos más pequeños son los que utilizan inductores activos y los más grandes utilizan elementos de línea de transmisión distribuida.

A veces el papel principal de un filtro es limitar el rango dinámico de señales presentadas a los circuitos activos, limitando así la distorsión. Claramente, los filtros activos no son adecuados cuando las grandes señales fuera de banda son una preocupación.

2.17.1 Radiofrecuencia Filtros activos

Hay varios problemas con los filtros de elementos grumosos. Los filtros de alto orden requieren muchos polos y ceros que deben colocarse con precisión, requiriendo pequeñas tolerancias. Con los filtros activos es posible, hasta cierto punto, lograr filtros de orden superior con menos elementos reactivos y así el problema de tolerancia se reduce considerablemente. Además, hay algunos diseños que se pueden afinar electrónicamente. Los filtros pasabanda y los filtros paso alto de elementos agrupados requieren inductores. Los inductores son un problema importante, ya que los inductores de RF tienen pérdidas y también solo se pueden obtener valores relativamente pequeños. Los inductores en chip ocupan un área considerable y, por lo tanto, pueden dominar el costo de los RFIC. Con los filtros activos, la retroalimentación y los condensadores se pueden usar para realizar características similares a inductores, definidas como una impedancia imaginaria positiva que aumenta con la frecuencia al menos en un rango de frecuencia pequeño. Muchas veces, y especialmente a frecuencias de radio más bajas, ya no se requieren inductores agrupados. El tamaño de los condensadores en los filtros es otro problema, y usando retroalimentación y ganancia, se puede aumentar el valor efectivo de los condensadores. Todo esto viene con límites. El límite principal es que la frecuencia de corte de los transistores debe ser mucho mayor que la frecuencia de funcionamiento de los filtros. Este es un costo incurrido cada vez que se utilizan comentarios. Una regla general aproximada es que la frecuencia de corte del transistor debe ser aproximadamente\(10\) veces la frecuencia de operación. Entonces, para un filtro de\(5\text{ GHz}\) paso de banda, se requiere un proceso de\(50\text{ GHz}\) transistor. El otro costo significativo es que los filtros activos solo son adecuados para señales pequeñas. La eficiencia, una medida de la cantidad de energía de CC utilizada en la producción de la señal de salida de RF, no es entonces una consideración. No se pueden usar filtros activos donde es probable que los niveles de señal sean grandes (como en la salida de un amplificador de potencia o en la entrada del receptor, debido a señales probables fuera de banda).

El aspecto esencial de los filtros activos de baja RF es el uso de retroalimentación, con elementos de retroalimentación reactivos, para realizar una función de transferencia de dominio de frecuencia con polos y ceros. El objetivo no es sintetizar condensadores e inductores efectivos, sino enfocarse en la respuesta general. Los filtros activos generalmente se desarrollan como etapas, con cada etapa realizando una función de transferencia de segundo o superior orden. El diseño es impulsado por simulación, ya que esta es la única forma de dar cuenta de los parásitos activos del dispositivo.

En el diseño de amplificadores operacionales, la retroalimentación se utiliza para lograr estabilidad de ganancia, pero a costa de reducir el ancho de banda. Si se utilizan elementos de retroalimentación reactiva, las funciones de transferencia de orden superior se pueden obtener con solo unos pocos elementos reactivos. En la Figura\(\PageIndex{1}\), una red de muesca Twin-T está conectada en la ruta de realimentación del amplificador operacional para obtener un filtro de paso de banda [27]. Lejos de la frecuencia de muesca, la trayectoria de retroalimentación tiene una alta impedancia y la ganancia general del amplificador disminuye. A medida que la frecuencia de la señal se acerca a la frecuencia de muesca, la trayectoria de retroalimentación se vuelve efectiva y la ganancia del amplificador La frecuencia de muesca\(f_{n}\),, es proporcional al producto RC de los componentes de retroalimentación y la\(Q\) es proporcional a la ganancia del amplificador. Las ecuaciones gobernantes para este filtro son

\[\label{eq:1}f_{n}=1/(2\pi RC)\quad\text{and}\quad Q=(1+G)/4 \]

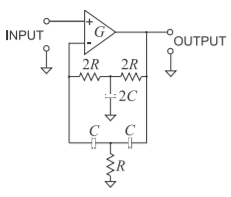
Figura\(\PageIndex{1}\): Filtro de paso de banda Twin-T activo: frecuencia central\(f_{0} = \pi RC/4\) y\(Q = (G + 1)/4\).

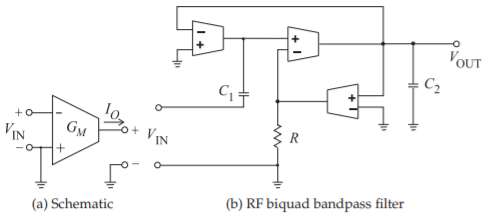
Figura\(\PageIndex{2}\): Amplificador de transconductancia operacional con transconductancia\(G_{M}\). En (a)\(I_{O} = G_{M}V_{\text{IN}}\).

2.17.2 Filtros bicuadráticos

Los filtros bicuadráticos son una clase importante de filtros y son el bloque básico utilizado en los filtros activos analógicos y RF. Los filtros biquad suelen utilizar amplificadores operacionales de transconductancia (OTA), cuyo esquema se muestra en la Figura\(\PageIndex{2}\) (a). Aquí\(I_{O} = G_{M} V_{\text{IN}}\), que es también la característica básica de un transistor individual. Estos circuitos tienen características típicas de los amplificadores operativos, incluyendo estabilidad de ganancia y resistencia a variaciones de tolerancia de componentes. Los filtros basados en OTA tienen la ventaja de una fácil sintonización, con frecuencias polares y cero ajustables electrónicamente. Un filtro biquad paso banda RF se muestra en la Figura\(\PageIndex{2}\) (b). Etapas como esta se conectan en cascada para realizar filtros de alto orden.

Los filtros bicuadráticos implementan la función de transferencia

\[\label{eq:2}H(s)=\frac{V_{\text{OUT}}}{V_{\text{IN}}} =\frac{N(s)}{D(s)}=\frac{a_{2}s^{2}+a_{1}s+a_{0}}{s^{2}+b_{1}s+b_{0}}=\frac{a_{2}(s+z_{1})(s+z_{2})}{(s+p_{1})(s+p_{2})} \]

Esto se conoce como una función bicuadrática y los filtros que implementan esta función se denominan filtros bicuadráticos o simplemente filtros bicuadráticos. Existen varios tipos especiales de filtros biquad.

La forma de la función bicuadrática para un filtro de paso bajo de segundo orden es

\[\label{eq:3}H_{\text{LP}}(s)=\frac{a_{0}}{s^{2}+b_{1}s+b_{0}}=\frac{K\omega_{p}^{2}}{s^{2}+(\omega_{p}/Q_{p})s+\omega_{p}^{2}} \]

\(H_{\text{LP}}(s)\)tiene un doble cero at\(s =\infty\) y, por lo tanto, una respuesta insignificante a frecuencias muy altas.

La forma de paso alto del filtro bicadrático se describe por

\[\label{eq:4}H_{\text{HP}}(s)=\frac{a_{2}s^{2}}{s^{2}+b_{1}s+b_{0}}=\frac{Ks^{2}}{s^{2}+(\omega_{p}/Q_{p})s+\omega_{p}^{2}} \]

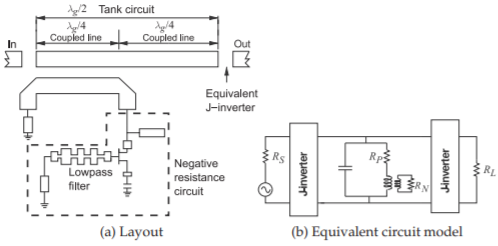
Figura\(\PageIndex{3}\): Filtro distribuido acoplado activo. Después [30].

La respuesta de\(H_{\text{HP}}(s)\) a altas frecuencias es\(K\) y la respuesta a frecuencias muy bajas va a cero.

La forma de paso de banda del filtro bicadrático se describe por

\[\label{eq:5}H_{\text{BP}}(s)=\frac{a_{1}s}{s^{2}+b_{1}s+b_{0}}=\frac{K(\omega_{p}/Q_{p})s}{s^{2}+(\omega_{p}/Q_{p})s+\omega_{p}^{2}} \]

La respuesta de\(H_{\text{BP}}(s)\) a frecuencias altas y bajas va a cero, y solo en y cerca de la frecuencia central\(\omega =\omega_{p}\),, hay una respuesta razonable.

La forma de rechazo de banda o muesca del filtro bicadrático se describe mediante

\[\label{eq:6}H_{\text{BR}}(s)=\frac{a_{2}s^{2}+a_{0}}{s^{2}+b_{1}s+b_{0}}=\frac{K(s^{2}+\omega_{z}^{2})}{s^{2}+(\omega_{p}/Q_{p})s+\omega_{p}^{2}} \]

La respuesta de\(H_{\text{BR}}(s)\) a frecuencias altas y bajas es alta, pero hay un doble cero en la frecuencia notch,\(\omega =\omega_{z}\), donde la respuesta es muy baja.

Con todos los filtros bicadráticos, la nitidez de la respuesta está determinada por\(Q_{p}\). La frecuencia de borde o la frecuencia central es\(\omega_{p}\) para los filtros de paso de banda, paso bajo y paso alto, y la frecuencia de muesca es\(\omega_{z}\) para el filtro de parada de banda.

2.17.3 Distribuidos Filtros Activos

A altas frecuencias de microondas, se pueden obtener buenos resultados combinando elementos distribuidos con una etapa de ganancia. Comúnmente los dispositivos activos se utilizan como dispositivos de acoplamiento. Se puede producir una resistencia negativa utilizando los dispositivos activos que pueden compensar las pérdidas asociadas con los elementos de la línea de transmisión o elementos pasivos agrupados en el filtro. El concepto utiliza un circuito de tanque resonante formado por una línea de transmisión o resonador de elementos grumados con una resistencia negativa acoplada al circuito del tanque por los dispositivos activos [28, 29, 30]. Este concepto se ilustra en la Figura\(\PageIndex{3}\). Aquí un resonador de media longitud de onda larga forma un circuito resonante (comúnmente llamado circuito de tanque en este contexto). Una resistencia negativa se acopla al circuito del tanque para compensar las pérdidas en el resonador y el resultado es efectivamente un circuito de tanque sin pérdidas.

Un circuito resonador activo se muestra en la Figura\(\PageIndex{4}\). El diseño del resonador sin pérdidas se basa en la resistencia negativa obtenida cuando el condensador está conectado a la fuente del MESFET. Este elemento en el

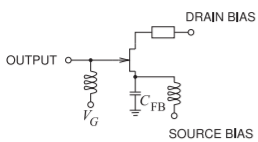
Figura\(\PageIndex{4}\): Un circuito resonador activo. Después [31].

proporciona una ruta de retroalimentación entre la salida del circuito, la tensión drenaje-tierra y la tensión de entrada puerta a fuente. Un aumento en la corriente drenaje-fuente conduce a un voltaje en la fuente que cambia el voltaje puerta-fuente. Esto induce una resistencia negativa que se ajusta a través de la capacitancia de retroalimentación,\(C_{FB}\), para compensar las pérdidas del inductor. Un inductor adicional,\(L_{P}\), se agrega en la puerta. El inductor resuena con la combinación en serie de\(C_{FB}\) y\(C_{GS}\). \(C_{FB}\)se puede implementar usando un diodo varactor para permitir la sintonización electrónica.