4.3: Ruido
- Page ID
- 85137
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Las fluctuaciones de voltaje y corriente surgen de varios procesos físicos diferentes que producen ruido con diversas propiedades estadísticas. Diversos tipos de ruido son importantes en los circuitos electrónicos y estos tipos van desde el ruido, como el ruido térmico, que se entiende muy bien, hasta el ruido que se ha observado y que afecta seriamente el rendimiento de los circuitos de RF pero que no se entiende bien. Un ejemplo de esto último es el ruido de fase en osciladores que se manifiesta como fluctuaciones aleatorias de la fase o frecuencia de una señal de oscilación. Uno de los problemas para entender el ruido es que puede ser difícil describir un tipo particular de ruido tanto en el dominio de tiempo como de frecuencia. No todos los tipos de ruido pueden describirse de manera sencilla y no se entienden las fuentes de algunos tipos de ruido. El impacto del ruido en un sistema de RF se describe en el dominio de la frecuencia, mientras que los orígenes físicos del ruido deben estar necesariamente en el mundo real (es decir, el dominio del tiempo). El impacto del ruido también está en el dominio del tiempo, lo que resulta en errores de bits de una señal modulada digitalmente recibida, demodulada y procesada. El ruido que se origina en una fuente de ruido está conformado por las características de un circuito antes de que se observe externamente y, por lo tanto, la verdadera naturaleza del ruido se oscurece aún más.
4.2.1 Observaciones de espectros de ruido
El ruido en la electrónica se atribuye al movimiento aleatorio de los portadores y la mayoría de los tipos de ruido tienen una densidad espectral de potencia que es plana con respecto a la frecuencia. Dicho ruido se denomina ruido blanco y si es filtrado, filtrado paso bajo o filtrado paso banda, se denomina ruido gaussiano blanco aditivo (AWGN) ya que el ruido tiene entonces una distribución estadística gaussiana asumada. El ruido mejor entendido es el ruido térmico y se atribuye al movimiento aleatorio de los electrones debido a la vibración aleatoria de la red de un material conductor. La teoría del ruido térmico se basa en el teorema de fluctuación-disipación [1] que puede ser utilizado para la mayoría de los materiales en equilibrio térmico. Este teorema se aplica tanto a los sistemas mecánicos clásicos como cuánticos y describe el ruido clásico encontrado hasta varios terahercios así como los efectos cuántico-mecánicos que dan forma al ruido por encima de unos pocos terahercios a temperatura ambiente o a frecuencias mucho más bajas a medida que la temperatura se acerca al cero absoluto [2].
El teorema de fluctuación-disipación relaciona las fluctuaciones inducidas térmicamente en un material con la resistencia del material. El origen físico del ruido térmico es el efecto neto de las corrientes rápidamente fluctuantes resultantes de las fluctuaciones térmicas de los electrones libres en un material resistivo (o conductor). Las fluctuaciones de los electrones son el resultado de las vibraciones de los átomos en la red de un material. Estas vibraciones se relacionan directamente con la temperatura y la temperatura se considera como una medida directa del estado de entropía o vibración aleatoria de la celosía. Entonces el teorema de fluctuación-disipación describe cómo la vibración (es decir, la temperatura) de la red induce pequeñas fluctuaciones de corriente en un material y así describe cómo la energía térmica se convierte en la energía eléctrica conocida como ruido Johnson. Esto es lo opuesto al efecto de la resistencia que convierte la energía eléctrica en energía térmica cuando el movimiento de los electrones (como corriente) hace que la red vibre más. Por lo que no es de extrañar que la corriente de ruido esté directamente relacionada con la resistencia.
Los resultados clave del teorema de fluctuación-disipación son que la potencia de ruido disponible de una resistencia o grupo de resistencias es linealmente proporcional a la temperatura, la potencia de ruido disponible es independiente del valor de la resistencia y que la densidad espectral de potencia (en vatios por hercio) es independiente de la frecuencia, es decir, es blanco, hasta unos pocos terahercios a temperatura ambiente.
Considere el bloque de material resistivo en la Figura\(\PageIndex{1}\) (a). Las vibraciones de celosía provocan un movimiento aleatorio de electrones y, por lo tanto, hay una miríada de pequeñas fuentes de corriente. El bloque de material resistivo tiene terminales y en esos terminales se puede medir una resistencia. La aplicación del teorema de fluctuación-disipación determina que el efecto neto de las pequeñas fuentes de corriente de ruido en el material es el mismo que el de una fuente de corriente en paralelo
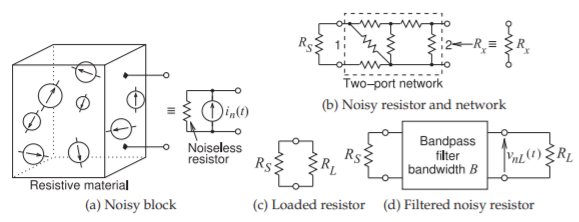
Figura\(\PageIndex{1}\): Redes resistivas ruidosas
con la resistencia efectiva como se muestra en la Figura\(\PageIndex{1}\) (a). La fuente de corriente de ruido\(i_{n}(t)\),, tiene propiedades estadísticas tales que la potencia de ruido disponible es proporcional al ancho de banda sobre el que se mide la potencia de ruido y a la temperatura del material en kelvin. Si el material resistivo está a una temperatura\(T_{0}\), entonces la temperatura de ruido del material\(T_{0}\). Yendo un paso más allá, se puede imaginar que el material resistivo puede ser descrito por una red de resistencias como se muestra en la Figura\(\PageIndex{1}\) (b). Si\(R_{S}\) y cada resistor en la red está a la misma temperatura\(T_{0}\), entonces toda la red, incluyendo\(R_{S}\), es equivalente tanto en términos de resistencia como de ruido a una sola resistencia ruidosa\(R_{x}\), es decir a\(T_{0}\). Por lo que la temperatura de ruido de la red resistiva es igual a la de\(R_{x}\) ambos siendo\(T_{0}\). Esto es cierto siempre que no haya fuentes de ruido no térmicas dentro de la red de dos puertos. Por ejemplo, si hubiera transistores entonces una fuente adicional de ruido es el ruido disparado. Entonces la temperatura del ruido que busca en el puerto\(2\) de la red sería mayor que la temperatura de ruido de la resistencia de la fuente en el puerto\(1\).
En la Figura\(\PageIndex{1}\) (c) una resistencia ruidosa\(R_{S}\) tiene una potencia de ruido disponible y toda esa potencia de ruido disponible se entrega a la carga\(R_{L}\) siempre que\(R_{L} = R_{S}\). (Toda la potencia de ruido disponible de también se\(R_{L}\) entregará a\(R_{S}\) bajo condiciones coincidentes). Incluso si una resistencia no está cargada, así\(R_{S}\) es por sí sola, habrá potencia de ruido en la resistencia que se generará y reabsorberá constantemente (a través del calentamiento resistivo) para que la resistencia esté en equilibrio térmico.
Una resistencia ruidosa es equivalente tanto eléctricamente como desde una perspectiva de ruido a una resistencia libre de ruido con una fuente de corriente de ruido en derivación como en la Figura\(\PageIndex{1}\) (a) o equivalentemente al mismo valor de resistencia con una fuente de voltaje de ruido (que se introducirá posteriormente). El voltaje de ruido y las fuentes de corriente son aleatorias y si el ruido es filtrado de paso bajo o paso de banda como en la Figura\(\PageIndex{1}\) (d), el voltaje de ruido resultante\(v_{nL}(t)\) a través de la carga libre de ruido tendrá estadísticas gaussianas. Dado que es inevitable que el ruido se filtre en un circuito, por ejemplo, habrá al menos capacitancias parasitarias, el ruido térmico a menudo se trata como ruido gaussiano blanco aditivo (AWGN) ya que sus propiedades estadísticas serán gaussianas. Esto es ciertamente fortuito ya que es posible simplificar en gran medida el tratamiento del ruido si se puede considerar aleatorio con las estadísticas gaussianas. Esto se explota en el desarrollo de las matemáticas de los procesos aleatorios en el Apéndice 1.A de [3], ya que se aplica tanto al ruido como a
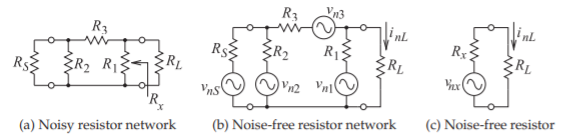
Figura\(\PageIndex{2}\): Ejemplo de atenuador.
señales moduladas digitalmente. El resultado clave es que el ruido puede describirse en el dominio de la frecuencia y esta comprensión y caracterización puede traducirse al mundo real, es decir, al dominio del tiempo.
Como ejemplo, es posible realizar un análisis de dominio de frecuencia del circuito mostrado en la Figura\(\PageIndex{2}\) (a) donde una fuente\(R_{S}\) se conecta a un atenuador resistivo y luego a una carga libre de ruido\(R_{L}\). Como de costumbre las resistencias emparejadas externas a los dos puertos son las mismas aquí para que\(R_{S} = R_{L}\). La red de la Figura\(\PageIndex{2}\) (a) puede ser reemplazada por una red de resistencias libres de ruido con fuentes de voltaje de ruido\(v_{nS},\: v_{n1},\: v_{n2},\) y\(v_{n3}\). Las fuentes de voltaje de ruido son aleatorias e independientes y por lo tanto no están correlacionadas. De esta manera evaluar la corriente de ruido\(i_{nL}\) en\(R_{L}\) las potencias de las contribuciones individuales para\(i_{nL}\) que sea necesario sumar primero. Esto se puede mostrar como idéntico al cálculo\(i_{nL}\) en la Figura\(\PageIndex{2}\) (c) donde se encuentra la resistencia equivalente\(R_{x}\) de la red y luego la fuente de voltaje de ruido,\(v_{nx}\) para esa resistencia utilizada. Por supuesto ya que el de dos puertos es un atenuador\(R_{x} = R_{S} = R_{L}\).
4.2.2 Caracterización del Ruido Térmico
Si bien el impacto del ruido en los circuitos de RF se mide y categoriza en el dominio de la frecuencia, las fuentes físicas de ruido están en el mundo real. El ruido en un conductor se manifiesta como fluctuaciones aleatorias en el tiempo de voltaje y corriente. Si bien es aleatorio, el ruido puede tener diferentes estadísticas dependiendo de cómo se origina. Las tres principales fuentes físicas de ruido que afectan a los circuitos electrónicos son la térmica, el disparo y el parpadeo.
El ruido térmico se conoce más formalmente como ruido Johnson-Nyquist y también se conoce como ruido Johnson o ruido Nyquist. El ruido se debe a fluctuaciones aleatorias de los portadores de carga dentro de un conductor que ocurren con o sin voltaje o corriente aplicados. Una resistencia a temperatura ambiente (\(290– 298\text{ K}\)o\(19–25^{\circ}\text{C}\)) tiene una potencia de ruido disponible de\(−174\text{ dBm}\) en\(1\) hercios de ancho de banda. El ruido no está correlacionado de manera que se sumará la potencia de ruido en un segundo hercio de ancho de banda. Entonces en\(2\) hercios de ancho de banda la potencia de ruido disponible es\((−174 + 3)\text{ dBm} = −171\text{ dBm}\).
El grado de fluctuación es linealmente proporcional a la temperatura absoluta. También la potencia de ruido generada es independiente de la resistencia del conductor. La derivación original del ruido térmico se debe a Nyquist [4], quien demostró que la densidad espectral de potencia (PSD) de la potencia de ruido disponible de una resistencia (de cualquier valor) es
\[\label{eq:1}S_{t}(f)=kT \]
donde\(k\) esta la constante de Boltzmann y\(T\) es la temperatura en kelvin. El subíndice\(t\) aquí se utiliza para indicar ruido térmico. Las unidades SI de\(S_{t}\) son vatios por hercio pero se expresan más comúnmente como\(\text{dBm}\) por hercios. La potencia de ruido disponible en un ancho de banda\(B\) es (en unidades de vatios)
\[\label{eq:2}P_{t}(f)=kTB \]
Cuando los efectos cuánticos son importantes, la ecuación\(\eqref{eq:1}\) se modifica y el PSD de ruido térmico es
\[\label{eq:3}S_{t}(f)=\frac{hf}{e^{hf/kT}-1} \]
donde\(h\) está la constante de Plank. En Ecuación\(\eqref{eq:3}\)\(hf\) está la energía de un fotón de frecuencia\(f\) y\(kT\) es la energía térmica promedio (es decir, energía cinética vibracional) del material. Para determinar la frecuencia a la que se\(S_{t}\) puede utilizar la forma más simple de considere lo siguiente. A frecuencias bajas a moderadas La ecuación se\(\eqref{eq:3}\) puede expandir como
\[\label{eq:4}S_{t}(f)=\frac{hf}{1+(hf/kT)+\frac{1}{2}(hf/kT)^{2}+\ldots -1}\approx\frac{kT}{1+\frac{1}{2}(hf/kT)} \]
Por lo tanto, la potencia de ruido térmico disponible disminuirá a medida que aumenta la frecuencia, y está en la mitad de su valor de baja frecuencia a una frecuencia crítica\(f_{c} = 2kT/h\). A temperatura ambiente esto es aproximadamente\(12\text{ THz}\). Por lo que los efectos cuánticos sobre el ruido térmico no son motivo de preocupación a temperatura ambiente a frecuencias por debajo de unos pocos terahercios.
Amplios tratamientos modernos de ruido térmico están disponibles en [5] y [6].
Ejemplo\(\PageIndex{1}\): Available Noise Power
¿Cuál es la potencia de ruido disponible de una resistencia en un\(50\text{ MHz}\) ancho de banda y en\(20^{\circ}\text{C}\).
Solución
El PSD es, a partir de la ecuación\(\eqref{eq:1}\),
\[\begin{align}S_{t}(f)&= (1.381\cdot 10^{−23}\text{ J/K})\cdot ((273 + 20)\text{ K})\nonumber \\ \label{eq:5}&= 4.046\cdot 10^{−21}\text{ J}=4.046\text{ zJ} = 4.046\text{ zW/Hz} = −173.9\text{ dBm/Hz}\end{align} \]
Es decir,\(4.046\text{ zJ}\) (zepto julios). El ruido térmico a temperatura ambiente se suele tomar como\(−174\text{ dBm/Hz}\). Esta potencia de ruido se divide por igual entre ruido de amplitud y ruido de fase (cada uno es\(−177\text{ dBm/Hz}\)) [7]. \(S_{t}(f)\)se multiplica por el ancho de banda para obtener la potencia de ruido térmico total disponible, por lo que para un\(50\text{ MHz}\) ancho de banda, la potencia de ruido térmico es
\[\begin{align}P_{t}(f) &= (4.046\cdot 10^{−21}\text{ J})\times (50\cdot 10^{6}\text{ Hz})\nonumber \\ \label{eq:6}&= 2.023\cdot 10^{−13}\text{ J}\cdot\text{s}^{-1}= 202.3\text{ fW} = −100.1\text{ dBm}\end{align} \]
Esta es una potencia apreciable dado que los teléfonos celulares pueden operar con señales de recepción más pequeñas que\(−90\text{ dBm}\). Entonces la lección aquí es usar el ancho de banda más pequeño posible en los diseños.
4.2.3 Ruido ambiental
El ruido en los sistemas de RF y microondas incluye el ruido del entorno, así como el ruido generado dentro de la propia circuitería. El ruido del ambiente puede tener orígenes galácticos, cuando se le conoce como ruido de fondo cósmico, de radiación de cuerpo negro, o puede ser ruido generado artificialmente. En los sistemas de comunicación celular la principal fuente de interferencia proviene de otros teléfonos y estaciones base en el sistema celular. Siempre que esto sea uniformemente aleatorio sobre la banda de comunicación, puede tratarse como ruido aleatorio. El ruido uniformemente aleatorio (es decir, ruido blanco) puede ser modelado por una resistencia mantenida a lo que se llama la temperatura del ruido.
Una resistencia ruidosa genera ruido blanco que tiene un PSD plano, es decir, la densidad espectral del ruido es independiente de la frecuencia. Una resistencia ruidosa puede ser modelada por una resistencia libre de ruido y una fuente aleatoria de voltaje o corriente denotada por\(v_{n}\) y\(i_{n}\), respectivamente (ver Figura\(\PageIndex{3}\)). Las fuentes\(v_{n}\) y\(i_{n}\) son aleatorias y sus densidades espectrales,\(S_{vn}\) y\(S_{in}\) respectivamente, están relacionadas por
\[\label{eq:7}S_{vn}(f)=R^{2}S_{in}(f) \]
La densidad espectral de voltaje de ruido de una resistencia\(R\) a temperatura\(T\) es [8]
\[\label{eq:8}S_{vn}(f)=\frac{v_{n}^{2}}{B}=4kTR \]
para que
\[\label{eq:9}v_{n}^{2}=4kTBR \]
Aquí\(k\) está la constante de Boltzmann,\(T\) es la temperatura en kelvins, y\(B\) es el ancho de banda en hercios.
Es posible que la temperatura del ruido que se busca en un puerto de dos puertos sea menor que la temperatura ambiente y luego se use la temperatura de ruido efectiva de la estructura como una medida de la potencia de ruido disponible. Una situación típica es especificar el ruido que presenta una antena a un receptor. El ruido captado por una antena es del entorno con generalmente solo una pequeña porción del ruido proveniente de la propia antena. En ausencia de pérdida de antena, una antena apuntada al espacio tendrá una temperatura de ruido correspondiente a la radiación cósmica de fondo de microondas con una temperatura de ruido efectiva de aproximadamente\(3\text{ K}\).
Dos fuentes de voltaje de ruido,\(v_{n1}\) y\(v_{n2}\), en serie, pueden correlacionarse parcialmente. Entonces las dos fuentes de ruido pueden ser reemplazadas por una sola fuente\(v_{n}\), donde
\[\label{eq:10}v_{n}^{2}=v_{n1}^{2}+v_{n2}^{2}+2C_{n1, n2}v_{n1}v_{n2} \]
Aquí\(C_{n1,n2}\) está el coeficiente de correlación, y\(−1\leq C_{n1,n2}\leq 1\). Si las fuentes no están correlacionadas, como lo serían para dos resistencias,\(C_{n1,n2} = 0\) y
\[\label{eq:11}v_{n}^{2}=v_{n1}^{2}+v_{n2}^{2} \]
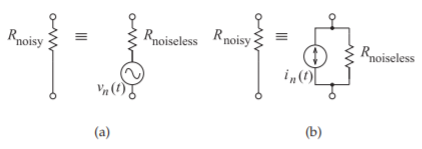
Figura\(\PageIndex{3}\): Circuitos equivalentes a ruido térmico: (a) resistencia ruidosa modelada como una resistencia libre de ruido en serie con una fuente de voltaje de ruido aleatorio\(v_{n}\); y (b) resistencia ruidosa modelada como una resistencia sin ruido en paralelo con una fuente de corriente de ruido aleatorio\(i_{n}\).
La correlación de las fuentes de ruido es importante para modelar el ruido en los transistores, ya que puede haber un origen físico común para el ruido que se modela como dos fuentes de ruido en un modelo de circuito.
4.2.4 Ruido Térmico y Capacitores
El ruido térmico también se ve con componentes reactivos como un condensador donde se conoce como ruido\(kT/C\) (leído como K-t-c). La resistencia en serie\(R\), de un condensador\(C\), aporta el ruido térmico pero la combinación RC también filtra el ruido. Este ruido se puede tratar de la misma manera que el análisis de ruido térmico anterior, pero hay una manera corta de mirar el ruido. Sarpeshkar et al. [9] mostraron que el voltaje de ruido cuadrático medio en un condensador de valor\(C\) dentro del ancho de banda de ruido del circuito RC (derivado como\(1/(4RC\)) en hercios) es
\[\label{eq:12}\overline{v}_{n}^{2}=\frac{kT}{C} \]
A temperatura ambiente (es decir,\(T = 20^{\circ}\text{C} = 293\text{ K}\)), el voltaje de ruido cuadrático medio,\(\sqrt{\overline{v}_{n}^{2}}\), en un\(10\text{ pF}\) condensador con una resistencia en\(1\:\Omega\) serie está\(20\:\mu\text{V}\) en un\(25\text{ GHz}\) ancho de banda.
4.2.5 Fuente Física de Ruido de Disparo
El ruido de disparo se debe a la corriente transportada por portadores de carga discretos. Es importante cuando hay una región que es escasa de transportistas libres. El ruido de disparo es particularmente importante con los dispositivos semiconductores, pero fue observado por primera vez por Schottky en 1926 en tubos de vacío. En un semiconductor los portadores de carga, electrones y agujeros, son discretos e independientes. Como tal, la corriente fluctúa a medida que el número de portadoras varía en pasos discretos. En promedio hay una velocidad neta de portadores que pasan un punto por intervalo de tiempo. Para que el ruido de disparo se observe por encima del ruido térmico, los portadores deben estar limitados a pasar en una sola dirección. Esta es la situación en muchos dispositivos semiconductores donde la región de agotamiento formada en la interfaz de las uniones pn obliga a la corriente a fluir en una sola dirección. El ruido de disparo es más significativo cuando el número de portadores de carga es pequeño, situación que también existe en los semiconductores. Sin embargo, incluso en un semiconductor, hay suficientes portadores para que el ruido de disparo tenga una distribución gaussiana de manera que estadísticamente se vea como ruido térmico [10]. Cuanto más corta sea la escala de tiempo crítica, y para los circuitos de microondas y RF este es el período de la forma de onda, menor será el número de portadoras que pasarán un punto y mayores serán las contribuciones fraccionarias de las fluctuaciones en los números de portadoras.
La fluctuación de corriente RMS debida al ruido de disparo es
\[\label{eq:13}\sigma_{i}=\sqrt{2eIB} \]
donde\(e\) esta la carga elemental,\(B\) es el ancho de banda en hercios, y\(I\) es la actual. Para una corriente CC de\(1\text{ mA}\) y en un\(1\text{ Hz}\) ancho de banda, la fluctuación de corriente RMS debida al ruido de disparo es\(\sigma_{i} = 18\text{ pA}\). Si esta corriente fluye a través de una resistencia\(R\), la densidad de ruido espectral en la resistencia es
\[\label{eq:14}P_{s}=2e|I| \]
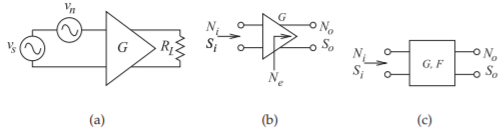
Figura\(\PageIndex{4}\): Ruido y dos puertos: (a) amplificador; (b) amplificador con exceso de ruido; y (c) red ruidosa de dos puertos.
Tenga en cuenta que\(P_{s}\) es independiente de la temperatura y la frecuencia, aunque eventualmente los efectos cuánticos se vuelven importantes [11]. En contraste, el ruido térmico es proporcional a la temperatura. La corriente en Ecuación\(\eqref{eq:14}\) es la corriente instantánea. Así que el ruido de disparo varía durante un ciclo de RF ya que el flujo de corriente varía. Si la corriente CC es mucho mayor que la corriente variable en el tiempo, entonces el ruido que se crea por los pulsos separables tiene un espectro de frecuencia plano y puede modelarse mediante una fuente de ruido blanco.
Entonces la lección aquí es que en los diseños de circuitos activos, las corrientes de polarización deben minimizarse. También tenga en cuenta que la potencia de ruido es una función del valor de resistencia pero los circuitos activos con valores de resistencia altos también tienden a tener bajos niveles de corriente.
4.2.6 Fuente Física de Ruido de Parpadeo
El tercer tipo de ruido que preocupa a los circuitos de RF y microondas es el ruido de parpadeo, a veces llamado ruido\(1/f\) (uno sobre f) debido a su forma de densidad espectral de potencia. El ruido de parpadeo se debe a la difusión, las trampas en un semiconductor y las trampas de superficie. Un portador libre es inmovilizado o atrapado cuando cae en una trampa, es decir, un centro de recombinación. Cuando varios de estos portadores están atrapados, significa que no están disponibles para conducción y como resultado, se modula la resistencia del semiconductor. Estas fluctuaciones tienen múltiples tiempos de relajación. El ruido de parpadeo se considera nuevamente en la Sección 6.4 en lo que respecta a la caracterización de los módulos osciladores locales. Una comprensión física completa del ruido de parpadeo no está disponible, y el ruido de parpadeo es una preocupación importante con los osciladores.

