4.4: Caracterización del ruido

Los amplificadores, filtros y mezcladores en un proceso frontal de RF (por ejemplo, amplificar, filtrar y mezclar) ingresan ruido de la misma manera que una señal de entrada. Además, estos componentes aportan exceso de ruido propio. Sin pérdida de generalidad, la siguiente discusión considera el ruido con respecto al amplificador mostrado en la Figura 4.2.4 (a), donde\(v_{s}\) está la señal de entrada. El desarrollo aquí se aplica solo al ruido blanco (es decir, ruido térmico y de disparo). La señal de ruido, con fuente designada por\(v_{n}\), es no correlacionada y aleatoria, y se describe como una tensión RMS o por su potencia de ruido.

La métrica más importante relacionada con el ruido es la SNR. Denotando la entrada de potencia de ruido al amplificador como\(N_{i}\), y denotando la entrada de potencia de señal al amplificador como\(S_{i}\), la relación de potencia de señal a ruido de entrada es\(\text{SNR}_{i} = S_{i}/N_{i}\). Si el amplificador está libre de ruido, entonces el ruido de entrada y las potencias de la señal son amplificadas por la ganancia de potencia del amplificador,\(G\). Por lo tanto, la potencia de ruido de salida es\(N_{o} = GN_{i}\), la potencia de señal de salida es\(S_{o} = GS_{i}\), y la SNR de salida es\(\text{SNR}_{o} = S_{o}/N_{o} = \text{SNR}_{i}\).

En la práctica, un amplificador es ruidoso, con la adición de exceso de ruido,\(N_{e}\), indicado en la Figura 4.2.4 (b). El exceso de ruido se origina en diferentes componentes en el amplificador y se hace referencia a la entrada o a la salida del amplificador. Más comúnmente se hace referencia a la salida para que la potencia total de ruido de salida sea\(N_{o} = GN_{i} + N_{e}\). En ausencia de calificador, se debe suponer que el exceso de ruido se refiere a la salida. \(N_{e}\)no se mide directamente. En cambio, la relación entre la SNR en la entrada y la de la salida es el factor de ruido:

\[\label{eq:1}F=\frac{\text{SNR}_{i}}{\text{SNR}_{o}} \]

y esta es la forma en que normalmente se mide el rendimiento del ruido. Si el circuito está libre de ruido, entonces\(\text{SNR}_{o} = \text{SNR}_{i}\) y\(F = 1\). Si el circuito no está libre de ruido, entonces\(\text{SNR}_{o} < \text{SNR}_{i}\) y\(F > 1\). \(F\)puede estar relacionado con el exceso de ruido producido en el circuito. Con el exceso de ruido,\(N_{e}\), referido a la salida del circuito,

\[\begin{align}F&=\frac{\text{SNR}_{i}}{\text{SNR}_{o}}=\frac{\text{SNR}_{i}}{1}\frac{1}{\text{SNR}_{o}}=\frac{S_{i}}{N_{i}}\frac{N_{o}}{S_{o}}=\frac{S_{i}}{N_{i}}\frac{GN_{i}+N_{e}}{GS_{i}}\nonumber \\ \label{eq:2}&=1+\frac{N_{e}}{GN_{i}}\end{align} \]

Una de las conclusiones que se pueden extraer de esto es que el factor de ruido,\(F\), depende de la potencia de ruido disponible en la entrada del circuito. Como referencia estándar, se utiliza la potencia de ruido disponible\(N_{R}\), de una resistencia a temperatura estándar,\(T_{0}\)\((290\text{ K})\) [12], y sobre un ancho de banda,\(B\) (in\(\text{Hz}\)),

\[\label{eq:3}N_{i}=N_{R}=kT_{0}B \]

donde\(k (= 1.381\times 10^{−23}\text{ J/K})\) está la constante de Boltzmann. Si la entrada de un amplificador está conectada a esta resistencia y toda la potencia de ruido se entrega al amplificador, entonces

\[\label{eq:4}F=1+\frac{N_{e}}{GN_{i}}=1+\frac{N_{e}}{GkT_{0}B} \]

Varios procesos físicos aleatorios dentro de un circuito contribuyen al exceso de ruido, y no todos estos procesos varían linealmente con la temperatura. En consecuencia\(F\) es una función de la temperatura, aunque suele ser débil. También es una función del ancho de banda, y existe un problema en el uso\(F\) con sistemas en cascada en los que los anchos de banda varían para diferentes subsistemas. Incluso con todos estos problemas,\(F\) es la medida más importante utilizada para caracterizar el rendimiento del ruido. Se puede utilizar para determinar el rendimiento de ruido de una cascada, cuando se conocen los factores de ruido y las ganancias de los constituyentes del subsistema. \(F\)es la relación de potencias, y cuando se expresa en decibelios, se utiliza la cifra de ruido (NF):

\[\begin{align}\text{NF}&=10\log_{10}F\nonumber \\ \label{eq:5}&=\text{SNR}_{i}|_{\text{dB}}-\text{SNR}_{o}|_{\text{dB}}\end{align} \]

donde la SNR se expresa en decibelios.

Considera el amplificador en la Figura 4.2.4. Si se ignora la contribución de ruido en exceso de un amplificador, la potencia de ruido de salida será

\[\label{eq:6}N_{o}=GkT_{0}B \]

Con el exceso de ruido del amplificador,\(N_{e}\), incluido, la potencia de ruido de salida es

\[\begin{align}N_{o}&=GkT_{0}B+N_{e}=GkT_{0}B(1+N_{e}/(GkT_{0}B))\nonumber \\ \label{eq:7}&=FGkT_{0}B\end{align} \]

Reordenando esta ecuación, el exceso de potencia de ruido se puede escribir como

\[\label{eq:8}N_{e}=(F-1)GkT_{0}B \]

El ruido de salida de un sistema se puede expresar en términos de su cifra de ruido. De la ecuación\(\eqref{eq:4}\), el ruido de salida es

\[\label{eq:9}N_{o}=GN_{i}+N_{e}=FGN_{i} \]

Es decir,

\[\label{eq:10}N_{o}|_{\text{dBM}}=\text{NF}+G|_{\text{dB}}+N_{i}|_{\text{dBM}} \]

Entonces, si el ruido de entrada de un amplificador con una ganancia de\(20\text{ dB}\) y una cifra de ruido de\(3\text{ dB}\) es\(−90\text{ dBm}\), entonces el ruido en la salida del amplificador es\(−67\text{ dBm}\). Este análisis del ruido de salida solo es correcto si la fuente de entrada es el equivalente a una resistencia mantenida a temperatura estándar,\(T_{0}\). Por lo que el análisis no se aplicaría si la entrada al sistema fuera una antena apuntando hacia el cielo (alejada de objetos cósmicos como el sol y la luna) que tendría una temperatura de ruido de\(4\text{ K}\) (debido a la radiación cósmica de fondo) más ruido de antena y cable.

Ejemplo\(\PageIndex{1}\): Effective Noise Temperature

Una antena con una temperatura de ruido de\(50\text{ K}\) está conectada a un amplificador con un ancho de banda de\(20\text{ MHz}\), una cifra de ruido de\(3\text{ dB}\), y una ganancia de\(10\text{ dB}\). ¿Cuál es la temperatura efectiva del ruido en la salida del amplificador?

Solución

La temperatura efectiva de ruido de salida\(T_{\text{eff}}\),, es la temperatura de una resistencia que produciría la misma potencia de ruido disponible,\(N_{o}\), como la potencia de ruido disponible de salida del amplificador. El amplificador agrega exceso de ruido,\(N_{e}\), al ruido de entrada,\(N_{i}\), que es amplificado por el amplificador. Entonces para determinar\(N_{o}\), se\(N_{e}\) debe determinar primero. Esto se obtiene de la cifra de ruido,\(\text{NF}\), que se define en términos de potencia de ruido de una resistencia en la entrada con una temperatura de\(T_{0} = 290\text{ K}\).

El factor de ruido\(F = 10^{\text{NF}} = 1.995\) y de la ecuación\(\eqref{eq:8}\)

\[\begin{align}N_{e}&= (F − 1)GkT_{0}B = (1.995 − 1)\cdot 10^{10/10}\cdot (1.3807\cdot ^{−23}\text{ J/K})\cdot (290\text{ K})\cdot (20\cdot 10^{6}\text{ Hz})\nonumber \\ \label{eq:11} &=7.969\cdot 10^{-13}\text{ W}\end{align} \]

El ruido de entrada de una resistencia en\(50\text{ K}\) es

\[\label{eq:12}N_{i}=kTB= (1.3807\cdot^{−23}\text{ J/K})\cdot (50\text{ K})\cdot (20\cdot 10^{6}\text{ Hz}) = 1.381\cdot 10^{−14}\text{ W} \]

Entonces, la potencia total de ruido de salida es

\[\label{eq:13}N_{o} = GN_{i} + N_{e} = 10^{10/10}\cdot 1.381\cdot 10^{−14} + 7.969\cdot 10^{−13} = 9.350\cdot 10^{−13}\text{ W} \]

Así, la temperatura efectiva del ruido en la salida del amplificador es

\[\label{eq:14}T_{\text{eff}}=\frac{N_{o}}{kB}=\frac{9.350\cdot 10^{-13}\text{ W}}{(1.3807\cdot ^{−23}\text{ J/K})\cdot (20\cdot 10^{6}\text{ Hz})}=3386\text{ K} \]

Ejemplo\(\PageIndex{2}\): Noise Figure of an Attenuator

¿Cuál es la cifra de ruido de un\(20\text{ dB}\) atenuador en un\(50\:\Omega\) sistema?

Solución

Denotando que el atenuador está en un\(50\:\Omega\) sistema indica que un modelo de circuito apropiado para usar en el análisis consiste en el atenuador accionado por un generador con una impedancia de\(50\:\Omega\) fuente, y el atenuador acciona una\(50\:\Omega\) carga. Además, la impedancia de entrada del atenuador terminado es\(50\:\Omega\), al igual que la impedancia que busca en la salida del atenuador cuando está conectado a la fuente. El punto clave es que el ruido proveniente de la fuente es el ruido generado térmicamente en la impedancia de la\(50\:\Omega\) fuente, y este ruido es igual al ruido que se entrega a la carga, ya que también lo es la impedancia presentada a la carga\(50\:\Omega\). Entonces el ruido de entrada\(N_{i}\),, es igual al ruido de salida:

\[\label{eq:15}N_{o}=N_{i} \]

La señal de entrada es atenuada por\(20\text{ dB} (= 100)\), entonces

\[\label{eq:16}S_{o}=S_{i}/100 \]

y por lo tanto el factor de ruido es

\[\label{eq:17}F=\frac{SNR_{i}}{SNR_{o}}=\frac{S_{i}}{N_{i}}\frac{N_{o}}{S_{o}}=\frac{S_{i}}{N_{i}}\frac{N_{i}}{S_{i}/100}=100 \]

y la cifra de ruido es

\[\label{eq:18}\text{NF}=20\text{ dB} \]

Así, la cifra de ruido de un atenuador (o un filtro) es solo la pérdida del componente. Esto no es cierto para los amplificadores por supuesto, ya que hay otras fuentes de ruido, y la impedancia de salida de un transistor no es una resistencia térmica.

4.3.1 Ruido en un sistema en cascada

La sección 4.3 desarrolló las medidas del factor de ruido y la cifra de ruido para un puerto de dos puertos. Este resultado puede generalizarse para un sistema. Considerando la segunda etapa de la cascada en la Figura\(\PageIndex{1}\), el exceso de ruido en la salida de la segunda etapa, debido únicamente al ruido generado internamente en la segunda etapa, es

\[\label{eq:19}N_{2e}=(F_{2}-1)kT_{0}BG_{2} \]

Entonces la potencia total de ruido en la salida de una cascada de dos etapas es

\[\begin{align}N_{2o}&=(F_{2}-1)kT_{0}BG_{2}+N_{o,1}G_{2}\nonumber \\ \label{eq:20} &=(F_{2}-1)kT_{0}BG_{2}+F_{1}kT_{0}BG_{1}G_{2}\end{align} \]

Esto se basa en la suposición razonable de que el exceso de ruido agregado en una etapa no está correlacionado con el exceso de ruido de otras etapas, así como no está correlacionado con el ruido de entrada. Así se pueden sumar poderes. El segundo término

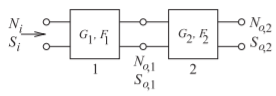
Figura\(\PageIndex{1}\): Dos puertos ruidosos en cascada.

en Ecuación\(\eqref{eq:20}\) es la salida de ruido de la primera etapa amplificada por la segunda etapa con ganancia\(G_{2}\).

Generalizar el resultado anterior produce la potencia de ruido total en la salida de la etapa\(m\) th:

\[\label{eq:21}N_{mo}=\sum_{n=2}^{m}\left[(F_{n}-1)kT_{0}B\prod_{j=2}^{n}G_{j}\right]+F_{1}kT_{0}B\prod_{n=1}^{m}G_{n} \]

Por lo tanto, una cascada de m etapas tiene un factor de ruido total del sistema en cascada de\(F^{T} =N_{mo}/(G^{T}N_{1i}0\),\(G^{T}\) siendo la ganancia total disponible en cascada y\(N_{1i}\) siendo la entrada de potencia de ruido a la primera etapa. En términos de los parámetros de etapas individuales, el factor de ruido total del sistema es

\[\label{eq:22}F^{T}=F_{1}+\frac{F_{2}-1}{G_{1}}+\frac{F_{3}-1}{G_{1}G_{2}}+\frac{F_{4}-1}{G_{1}G_{2}G_{3}}+\ldots \]

es decir,

\[\label{eq:23}F^{T}=F_{1}+\sum_{n=2}^{m}\frac{F_{n}-1}{\prod_{i=2}^{n}G_{i-1}} \]

Esta ecuación se conoce como la fórmula de Friis [13].

Nota

La fórmula de transmisión de Friis llamada similar se refiere a los sistemas de antenas.

Ejemplo\(\PageIndex{3}\): Noise Figure of Cascaded Stages

Considere la cascada de un amplificador diferencial y un filtro que se muestran en la Figura\(\PageIndex{2}\).

1. ¿Cuál es la ganancia de banda media del filtro en decibelios? Tenga en cuenta que IL es pérdida de inserción.
2. ¿Cuál es la cifra de ruido de banda media del filtro?
3. El amplificador tiene una ganancia\(G_{1} = 20\text{ dB}\) y una figura de ruido de\(2\text{ dB}\). ¿Cuál es la ganancia general del sistema de cascada en medio de la banda? Exprese su respuesta en decibelios.
4. ¿Cuál es el factor de ruido del sistema en cascada?
5. ¿Cuál es la cifra de ruido del sistema en cascada?

Solución

1. \(G_{2} = 1/\text{IL}\), por lo tanto\(G_{2} = −3\text{ dB}\).
2. Para un elemento pasivo,\(\text{NF}_{2} = \text{IL} = 3\text{ dB}\).
3. \(G_{1} = 20\text{ dB}\)y\(G_{2} = −3\text{ dB}\), entonces\(G_{\text{TOTAL}} = G_{1}|_{\text{dB}} + G_{2}|_{\text{dB}} = 17\text{ dB}\).
4. \(F_{1} = 10^{\text{NF}_{1}/10} = 10^{2/10} = 1.585,\: F_{2} = 10^{\text{NF}_{2}/10} = 10^{3/10} = 1.995,\: G_{1} = 10^{20/10} = 100,\)y\(G_{2} = 10^{−3/10} = 0.5\). Usando la fórmula de Friis
   \[\label{eq:24}F_{\text{TOTAL}}=F_{1}+\frac{F_{2}-1}{G_{1}}=1.585+\frac{1.995-1}{100}=1.594 \]
5. \(\text{NF}_{\text{TOTAL}}=10\log_{10}(\text{F}_{\text{TOTAL}})=10\log_{10}(1.594)=2.03\text{ dB}\)

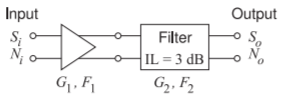
Figura\(\PageIndex{2}\): Amplificador diferencial seguido de un filtro diferencial.

Ejemplo\(\PageIndex{4}\): Noise Figure of a Two-Stage Amplifier

Considere un amplificador de\((20^{\circ}\text{C})\) dos etapas a temperatura ambiente donde la primera etapa tenga una ganancia de\(10\text{ dB}\) y la segunda etapa tenga una ganancia de\(20\text{ dB}\). La cifra de ruido de la primera etapa es\(3\text{ dB}\) y la segunda etapa es\(6\text{ dB}\). El amplificador tiene un ancho de banda de\(10\text{ MHz}\).

1. ¿Cuál es la potencia de ruido que se presenta al amplificador\(10\text{ MHz}\)?
2. ¿Cuál es la ganancia total del amplificador?
3. ¿Cuál es el factor de ruido total del amplificador?
4. ¿Cuál es la cifra de ruido total del amplificador?
5. ¿Cuál es la potencia de ruido en la salida del amplificador\(10\text{ MHz}\)?

Solución

1. La potencia de ruido de una resistencia a temperatura ambiente es\(−174\text{ dBm/Hz}\) (o más precisamente\(−173.86\text{ dBm/Hz}\) en\(293\text{ K}\)). En\(10\text{ MHz}\) el ruido de entrada se encuentra la potencia\(N_{i} = −173.86\text{ dBm} + 10 \log(10^{7}) = −173.86 + 70\text{ dBm} = −103.86\text{ dBm}\).
2. Ganancia total\(G^{T} = G_{1}G_{2} = 10\text{ dB} + 20\text{ dB} = 30\text{ dB} = 1000\).
3. \(F_{1} = 10^{\text{NF}_{1}/10} = 10^{3/10} = 1.995,\: F_{2} = 10^{\text{NF}_{2}/10} = 10^{6/10} = 3.981\). Usando la fórmula de Friis, la cifra de ruido total es\(F^{T}= F_{1} + \frac{F_{2} − 1}{G_{1}} = 1.995 + \frac{3.981 − 1}{10} = 2.393\).
4. La cifra de ruido total es\(\text{NF}^{\text{T}} = 10 \log_{10}(F^{T}) = 10 \log_{10}(2.393) = 3.79\text{ dB}\).
5. Potencia de ruido de salida en\(10\text{ MHz}\) ancho de banda es\(N_{o} = F^{T}kT_{0}BG^{T} = (2.393)\cdot (1.3807\cdot 10^{−23}\cdot\text{J}\cdot\text{K}^{−1})\cdot (293\text{ K})\cdot (10^{7}\cdot\text{s}^{−1})(1000) = 9.846\cdot 10^{−11}\text{ W} = −70.07\text{ dBm}\). Alternativamente,\(N_{o}|_{\text{dBm}} = N_{i}|_{\text{dBm}} + G^{T}|_{\text{dB}} + \text{NF}^{\text{T}} = −103.86\text{ dBm} + 30\text{ dB} + 3.79\text{ dB} = −70.07\text{ dBm}\).

4.3.2 Figura de medición de ruido

El método\(Y\) -factor es la base de los modernos sistemas automáticos de medición de cifras de ruido por microondas. La técnica consiste en medir la potencia de ruido en la salida de un dispositivo bajo prueba (DUT) cuando se conectan dos fuentes de ruido diferentes a la entrada del DUT [14]. La forma manual del método\(Y\) -factor se utiliza en frecuencias de onda milimétrica. El método depende de la precisión de la medición de ganancia, la capacidad de generar niveles precisos de exceso de potencia de ruido y la sensibilidad de la medición de la potencia de ruido. La medición de ganancia y potencia de ruido son sutilmente diferentes, con ganancia generalmente una medición coherente mientras que la medición de potencia de ruido es necesariamente incoherente. Tanto en sistemas automáticos como manuales, la configuración de medición es un sistema en cascada en el que el DUT es la primera etapa y el conjunto de prueba es el último y generalmente el segundo conjunto. La contribución de ruido del conjunto de prueba solo es insignificante si la ganancia del DUT es alta.

En condiciones coincidentes, la ganancia de potencia disponible del DUT es

\[\label{eq:25}G=\frac{S_{o}}{S_{i}} \]

por lo que la potencia de la señal se puede eliminar de la expresión para el factor de ruido combinando Ecuaciones\(\eqref{eq:1}\) y\(\eqref{eq:25}\):

\[\label{eq:26}F=\frac{\text{SNR}_{i}}{\text{SNR}_{o}}=\frac{S_{i}}{N_{i}}\frac{N_{o}}{S_{o}}=\frac{N_{o}}{N_{i}G} \]

El ruido de salida es mayor que el ruido de entrada amplificado debido al ruido insertado por el DUT. Denotando el componente de la potencia de ruido de salida debida

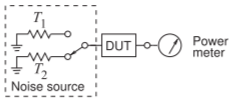
Figura\(\PageIndex{3}\): Configuración de prueba de figura de ruido para determinar la figura de ruido de un DUT.

únicamente al DUT por\(N_{D}\), la potencia de ruido de salida es

\[\label{eq:27}N_{o}=N_{i}G+N_{D} \]

El componente final del desarrollo es señalar que la potencia de ruido de entrada está relacionada con la temperatura de la coincidencia de entrada de manera que\(N_{i} = kTB\) donde\(k\) está la constante de Boltzmann y\(B\) está el ancho de banda de medición. Convencionalmente\(F\) se hace referencia a la temperatura estándar\(T_{0} = 290\text{ K}\) (específicamente la temperatura del ruido de entrada es\(T_{0}\)) y así

\[\label{eq:28}N_{D}=kT_{0}BG(F-1) \]

En el método\(Y\) -factor, se aplican dos fuentes de ruido con temperaturas de ruido conocidas\(T_{1}\) y\(T_{2}\) (con\(T_{2} > T_{1}\)) a la entrada del DUT y las correspondientes potencias de ruido de salida\(N_{1}\) y\(N_{2}\) se miden (ver Figura\(\PageIndex{3}\)). En el laboratorio se utiliza una fuente de ruido calibrada, como un diodo de polarización inversa en avalancha, para producir la fuente de ruido en\(T_{2}\). La otra temperatura,\(T_{1}\), a menudo se obtiene apagando la fuente de ruido para que\(T_{1} = T_{0}\), la temperatura ambiente. Esto lleva al\(Y\) factor, que se define como

\[\label{eq:29}Y=N_{2}/N_{1} \]

En el estado apagado, es decir\(T_{1} = T_{0}\), cuando, la potencia de ruido de salida en el estado apagado se denomina “apagado”:

\[\label{eq:30}N_{1}=kT_{0}BG+N_{D}=kT_{0}BG+kT_{0}BG(F-1) \]

La segunda fuente de ruido, con temperatura de ruido\(T_{2}\), produce un exceso de ruido calibrado y la potencia de ruido en estas condiciones se llama “on power”:

\[\label{eq:31}N_{2}=kT_{2}BG+N_{D}=kT_{2}BG+kT_{0}BG(F-1) \]

Combinando Ecuaciones\(\eqref{eq:28}\) —\(\eqref{eq:31}\) rendimientos

\[\label{eq:32}F=\frac{T_{2}-T_{0}}{T_{0}(Y-1)} \]

Expresar la ecuación\(\eqref{eq:33}\) en decibelios e integrar (quizás a través de la medición) sobre el ancho de banda del sistema produce la cifra de ruido,

\[\label{eq:33}\text{NF}=10\log(F)=\text{ENR}_{\text{dB}}-10\log(Y-1) \]

donde\(\text{ENR}_{\text{dB}} = 10 \log[(T_{2} − T_{0})/T_{0}]\) está la relación de exceso de ruido en decibelios de la fuente de ruido calibrada.

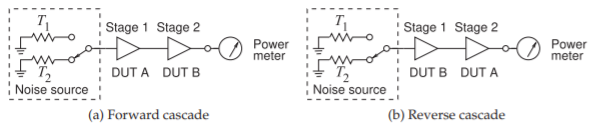
Figura\(\PageIndex{4}\):\(Y\) -prueba de factores que incorpora activamente el efecto de contribución de la segunda etapa.

4.3.3 Medición de la temperatura del ruido

Si se conoce la cifra de ruido de un amplificador que reemplaza al DUT, entonces se puede determinar la temperatura de ruido de una fuente. De la ecuación\(\eqref{eq:32}\),

\[\label{eq:34}T_{2}=FT_{0}(Y-1)+T_{0} \]

En una aplicación de laboratorio el amplificador podría enfriarse criogénicamente y luego hay un exceso de contribución de ruido insignificante por parte del amplificador para que\(F\approx 1\) y\(T_{2} = YT_{0}F\).

4.3.4 Medición de la Figura de Ruido de Dispositivos de Bajo Ruido

Uno de los factores que afecta la precisión de la determinación de la cifra de ruido es el ruido que se origina en el conjunto de prueba de medición Esto lleva a un error que a veces se denomina efecto de contribución de la segunda etapa [15]. Este es un tema particularmente importante a la hora de medir la cifra de ruido de los dispositivos de baja ganancia, ya que entonces la contribución de ruido de la segunda etapa puede ser significativa. Un enfoque para minimizar este error es la inserción de un amplificador de bajo ruido de alta ganancia, denominado amplificador de instrumentación, entre el DUT y el conjunto de prueba. La cifra de ruido del amplificador de instrumentación debe conocerse con precisión si el error que introduce se va a eliminar de la medición de la cifra de ruido bruto.

El método\(Y\) -factor se basa en que el amplificador de instrumentación tenga una cifra de ruido mucho menor que el DUT. Cuando esto no se puede lograr, lo mejor que se puede hacer es usar dos amplificadores (casi) idénticos con las mismas características de ganancia y ruido. La técnica\(Y\) de factor extendido descrita en esta sección utiliza dos DUTs en una cascada de dos etapas primero con una disposición de los DUTs y luego con la cascada inversa [16]. La técnica hace uso de la operación del factor de ruido en cascada dos veces. La figura\(\PageIndex{4}\) ilustra la configuración de prueba con las dos posibles disposiciones de los DUT en cascada. En\(\PageIndex{4}\) la Figura el medidor de potencia está configurado para medir la potencia de ruido (normalizada a un\(1\text{ Hz}\) ancho de banda).

Los factores de ruido individuales de los DUT para un sistema en cascada con DUT A seguido de DUT B, la cascada directa, se denotan por\(F_{1A}\) y\(F_{2B}\), y los de la cascada inversa con DUT B seguido de DUT A son\(F_{1B}\) y\(F_{2A}\). Las ganancias correspondientes de las etapas son\(G_{1A},\: G_{2B}\) para la cascada directa y\(G_{1B},\: G_{2A}\) para la cascada inversa. Aquí el primer subíndice se refiere a la posición en la cascada (ya sea primera o segunda etapa), y el segundo subíndice identifica el DUT particular (ya sea A o B). Finalmente, se denotan los factores de ruido totales de los sistemas en dos cascada\(F_{A}^{T}\) y de\(F_{B}^{T}\) acuerdo con

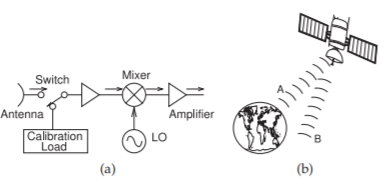
Figura\(\PageIndex{5}\): Radiómetro: (a) arquitectura heterodina que muestra el interruptor de calibración; y (b) radiómetro satelital que conmuta entre dos haces, uno orientado a la región que se está monitoreando y el otro en un espacio mucho más frío que sirve de calibración.

ya sea DUT A o DUT B es la primera etapa. Usando la fórmula de Friis para la cascada hacia adelante, la ecuación se\(\eqref{eq:23}\) puede escribir como,

\[\label{eq:35}F_{A}^{T}=F_{1A}+(F_{2B}-1)/G_{1A} \]

y para la cascada inversa

\[\label{eq:36}F_{B}^{T}=F_{1B}+(F_{2A}-1)/G_{1B} \]

La técnica presume que los parámetros de los DUTs son invariantes de su posición en la cascada de manera que\(F_{1A} = F_{2A} = F_{A}\) y así\(F_{1B} = F_{2B} = F_{B}\) como\(G_{1A} = G_{2A} = G_{A}\) y\(G_{1B} = G_{2B} = G_{B}\). Ecuaciones\(\eqref{eq:35}\) y ahora se\(\eqref{eq:36}\) pueden resolver simultáneamente para los factores de ruido desconocidos de las dos etapas:

\[\label{eq:37}F_{B} =[F_{B}^{T}G_{A}G_{B}-G_{A}(1 − F_{A}^{T}) − 1]/(G_{A}G_{B}) \]

y

\[\label{eq:38}F_{A}=[F_{A}^{T}G_{A}-F_{B}+1]/(G_{A}) \]

de la medida\(F_{A}^{T},\: F_{B}^{T},\: G_{A}\), y\(G_{B}\). Entonces, con las ganancias de las dos etapas medidas independientemente, los factores de ruido de las dos etapas se pueden determinar a partir de los factores de ruido medidos de las cascadas hacia adelante y hacia atrás.

En la situación especial de los DUT emparejados donde el ruido y la ganancia de las dos etapas son idénticos (de manera que\(F_{A} = F_{B} = F\) y\(G_{A} = G_{B} = F\)) y\(F_{A}^{T}= F_{B}^{T}= F^{T}\), luego los cálculos simplifican para producir el factor de ruido de cada etapa:

\[\label{eq:39}F=\frac{GF^{T}}{G^{2}+1} \]

Uno de los supuestos del método del factor Y extendido es que la ganancia y el ruido de las etapas son invariantes con respecto al orden de las etapas en la cascada. Cualquier salida resultará en un error. Una técnica que reduce la sensibilidad a la colocación es utilizar pequeños atenuadores en las entradas y salidas de las etapas. Las contribuciones de ruido se pueden eliminar del resultado final medido.

4.3.5 Sistema de Radiómetro

Un radiómetro, como se muestra en la Figura\(\PageIndex{5}\) (a), mide la potencia en la radiación EM predominantemente a frecuencias de microondas y más comúnmente mide el ruido. Los radiómetros se utilizan en teledetección y radioastronomía,

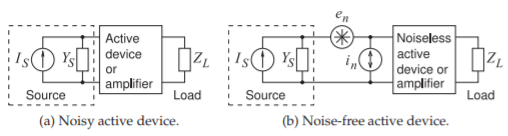
Figura\(\PageIndex{6}\): Modelo de amplificador para el cálculo del factor de ruido: (a) con dispositivo activo ruidoso o amplificador donde\(I_{S}\) está el generador de fuente y\(Y_{S}\) es la admitancia equivalente Norton de la fuente; y (b) con el dispositivo activo ruidoso o amplificador reemplazado por el voltaje de ruido\(e_{n}\), y corriente de ruido\(i_{n}\),, (las fuentes de ruido), y un dispositivo activo sin pérdidas o amplificador.

especialmente por satélites y aeronaves. Comprender el proceso físico que genera radiación no correlacionada a diferentes frecuencias permite identificar vegetación, temperaturas del aire y del mar, cobertura de hielo, salinidad oceánica y otras fuentes superficiales y atmosféricas a partir del espectro capturado por un radiómetro. Los radiómetros monitorean ventanas discretas del espectro, particularmente a frecuencias correspondientes a resonancias moleculares. Un radiómetro incluye un mecanismo de calibración rápida, como un interruptor Dicke, que cambia rápidamente entre el objeto que se observa y otro objeto que sirve como fuente de ruido calibrado. En aviones y en tierra, las fuentes de calibración son resistencias, a menudo mantenidas a bajas temperaturas. En la Figura\(\PageIndex{5}\) (b) se muestra un radiómetro basado en satélite, y en lugar de un interruptor Dicke, la calibración se obtiene conmutando el haz de antena entre la región observada (Haz A) y un área vacía del espacio (Haz B). Con un interruptor Dicke o conmutación de haz de antena, es posible lograr mejor que 0.01 K de resolución.

4.3.6 Figura de ruido de un amplificador de dos puertos

Los parámetros que definen la cifra de ruido de los amplificadores de dos puertos fueron establecidos por Haus et al. [12] en 1960 y son utilizados por fabricantes de transistores de microondas en sus hojas de datos. El modelo de amplificador utilizado en el cálculo del factor de ruido se muestra en la Figura\(\PageIndex{6}\).

La figura\(\PageIndex{6}\) tiene el dispositivo activo o amplificador, que es ruidoso, representado como un dos puertos con una fuente equivalente a Norton, que tendrá su propio ruido, y una carga. El dispositivo activo ruidoso o amplificador puede ser reemplazado por un dos puertos sin ruido con una fuente de ruido de voltaje,\(e_{n}\), y una fuente de ruido de corriente,\(i_{n}\), en la parte frontal de los dos puertos. Cualquier puerto lineal ruidoso puede ser representado por un puerto de dos puertos sin ruido con fuentes de ruido. Con un dispositivo activo o amplificador habrá muchas fuentes de ruido internas pero son las fuentes de ruido en la entrada, previas a la ganancia, las que son más significativas. Para un dispositivo activo o amplificador las fuentes de voltaje y corriente estarán al menos parcialmente correlacionadas y por lo tanto la admitancia de la fuente es importante para determinar cómo se combinan. Un peor de los casos sería cuando se combinan para presentar el máximo ruido posible en la entrada del dispositivo activo o amplificador. También es posible ajustar la admitancia de la fuente para que las fuentes de ruido se combinen para presentar el ruido mínimo al dispositivo activo o amplificador. Este efecto se captura en el factor de ruido del amplificador en la Figura\(\PageIndex{6}\). El factor de ruido de este amplificador es [12]

\[\label{eq:40}F=F_{\text{min}}+\frac{r_{n}}{g_{s}}\left| y_{s}-y_{\text{opt}}\right|^{2} \]

donde\(r_{n} = (R_{n}/Z_{0})\) se llama la resistencia al ruido equivalente de los dos puertos y\(F_{\text{min}}\) es el factor de ruido mínimo obtenido ajustando sintonizadores en la entrada del amplificador para presentar todos los valores posibles de\(Y_{S}\) a la entrada del amplificador. La admisión normalizada presentada por los sintonizadores en\(F_{\text{min}}\) es\(y_{\text{opt}}\). Con\(y_{s}(= Y_{S} /Z_{0})\) y\(g_{s} = \Re \{y_{s}\}\) siendo la admitancia y conductancia normalizadas reales, respectivamente, Ecuación\(\eqref{eq:40}\) permite calcular el factor de ruido para un diseño real. Los parámetros en Ecuación\(\eqref{eq:40}\) describen el efecto de las fuentes de ruido del amplificador interno y cómo se correlacionan.

Más comúnmente, los parámetros de ruido se reportan en términos de coeficientes de reflexión en lugar de admitancia. El coeficiente de reflexión fuente,\(\Gamma_{s}\), proviene de

\[\label{eq:41}y_{s}=\frac{1-\Gamma_{s}}{1+\Gamma_{s}} \]

y el coeficiente óptimo de reflexión fuente,\(\Gamma_{\text{opt}}\), proviene de

\[\label{eq:42}y_{\text{opt}}=\frac{1-\Gamma_{\text{opt}}}{1+\Gamma_{\text{opt}}} \]

Sustituir estos en Ecuación\(\eqref{eq:40}\) da como resultado

\[\label{eq:43}F=F_{\text{min}}+\frac{4r_{n}\left|\Gamma_{s}-\Gamma_{\text{opt}}\right|^{2}}{\left(1-|\Gamma_{s}|^{2}\right)\left|1+\Gamma_{\text{opt}}\right|^{2}} \]

Juntos\(F_{\text{min}},\: r_{n},\) y\(\Gamma_{\text{opt}}\) se llaman los parámetros de ruido de un dispositivo y deben medirse. Los parámetros de ruido de un transistor pHEMT se dan en la Tabla 4.4.1.

En general, el diseño para el mejor rendimiento de ruido no produce la mejor ganancia. Sin embargo, la reducción en la ganancia suele ser pequeña. El diseño de las redes de coincidencia de entrada y salida de un amplificador para ser emparejado conjugadamente produce la ganancia máxima del amplificador. Sin embargo, para obtener el mejor rendimiento de ruido, la red de coincidencia de entrada no coincide conjugadamente y en su lugar el coeficiente de reflexión de entrada que busca en la red coincidente desde el dispositivo activo lo es\(\Gamma_{\text{opt}}\). En consecuencia, no se obtiene ganancia máxima. La interpretación de por qué esto es necesario es que un desajuste particular minimiza las contribuciones de ruido combinadas de fuentes de ruido de dispositivos activos internos parcialmente correlacionados. En el diseño moderno de RF y microondas, sin embargo, si el rendimiento del ruido es preocupante, se utilizan dos o más etapas de amplificador, con la primera etapa diseñada para un rendimiento óptimo de ruido y etapas posteriores diseñadas para obtener la ganancia requerida.