4.8: Distorsión de Intermodulación Pasiva
- Page ID
- 85127
Distorsión de intermodulación pasiva (PIM) es el término utilizado para describir la distorsión no lineal que ocurre cuando los componentes pasivos son supuestamente lineales. Al igual que con los componentes no lineales como los amplificadores, la generación de tonos espurios puede inundar pequeñas señales recibidas. La prueba típica de PIM es una prueba de dos tonos en la que se aplican dos sinusoides grandes de igual amplitud al dispositivo bajo prueba (DUT) y se mide el nivel de las señales de intermodulación. A excepción del DUT que genera la distorsión siendo pasiva, la distorsión aparece como se describe en la Sección 4.5. La PIM se observa en un gran número de situaciones incluyendo cables coaxiales [33, 34], líneas de transmisión microstrip [35], atenuadores [36], terminaciones [37, 38], guías de onda rectangulares [39, 40], antenas y filtros [41, 42].
4.7.1 Fuentes de PIM
Se han identificado o sugerido varias causas de PIM. Estos incluyen efectos de autocalentamiento y unión no lineal cuando las corrientes fluyen de un metal a un metal diferente. El concepto es que los metales diferentes forman una característica débil de corriente-voltaje similar a un diodo [39].
El método más conveniente para medir pequeños niveles de PIM utiliza un filtro para separar una pequeña señal de intermodulación distorsionada de los dos tonos de conducción. La respuesta finita del filtro requiere que los tonos de RF estén al menos\(1\text{ MHz}\) separados. Sin embargo, la distorsión que es menor que la\(1\text{ MHz}\) de una señal es motivo de preocupación en los sistemas de RF. Varias mediciones han demostrado que el nivel de distorsión aumenta rápidamente a medida que el componente de distorsión se acerca en frecuencia a la señal de conducción [37].
La figura\(\PageIndex{1}\) muestra el PIM de tercer orden de terminaciones medidas en una prueba de dos tonos [43]. El nivel PIM se grafica contra la separación de frecuencias de los dos tonos. Se observan resultados similares con otros componentes incluyendo líneas de transmisión y antenas [35, 36, 37, 38]. La terminación de PIM baja, que resulta en la Curva (a) en la Figura\(\PageIndex{1}\), es la terminación PIM más baja disponible
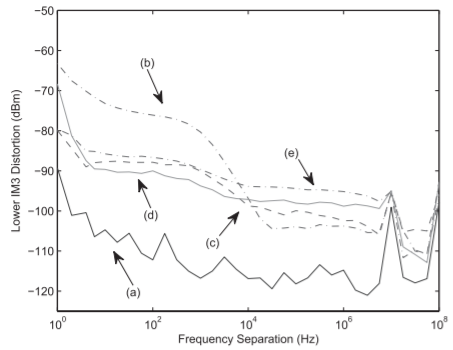
Figura\(\PageIndex{1}\): Distorsión de intermodulación pasiva de tercer orden medida (IM3 inferior) de terminaciones comunes de tipo N de alta potencia de laboratorio utilizando una prueba de dos tonos en\(460\text{ MHz}\): (a) terminación basada en cable de PIM baja; (b) parte PE6097, componente A; (c) parte PE6097, componente B; (d) parte PE6035, componente A; y e) parte PE6035, componente A. Medición tomada con potencia\(26\text{ dBm}\) de entrada para cada tono. Después [43].
que comprende, aquí, un cable\(100\text{ m}\) largo terminado ligeramente con pérdidas con una pérdida de\(0.1\text{ dB/m}\). La pérdida distribuida de bajo nivel extiende el calor generado a lo largo de una distancia considerable y por lo tanto hay un efecto PIM electrotérmico insignificante. Las curvas (b) y (c) representan el PIM medido para dos conectores de tipo N con aletas por lo demás idénticos. Las curvas (d) y (e) trazan el PIM medido para otro par de conectores. Se desconoce el motivo de la discrepancia. El rápido aumento de PIM por debajo de la separación de\(200\text{ Hz}\) tono se debe a los efectos electrotérmicos.
El rápido aumento en el nivel de PIM a medida que se reduce la separación de tonos se debe a los efectos electrotérmicos. Cuando están cerca en frecuencia, los dos tonos producen una forma de onda de latido que calienta periódicamente un conductor, cambiando su resistencia a través del coeficiente térmico de resistencia del conductor. Este cambio en la resistencia da como resultado una variación periódica de la relación corriente-voltaje (es decir, la ley de Ohm) que resulta en la generación de tonos de intermodulación. Se ha demostrado que si se evitan metales y materiales magnéticos disímiles, el PIM generado se debe enteramente a efectos electrotérmicos [37].
Con espaciamientos de tono superiores a unos pocos cientos de kilohercios, o en algunos casos algunos megahercios, el PIM se está generando a través de otro mecanismo. Se han postulado varias fuentes de este PIM, y si bien todas podrían ser fuentes físicas de PIM, que es lo más importante no está claro. Se ha demostrado que el PIM se debe casi en su totalidad a los efectos de densidad de corriente, por lo que reducir la densidad de corriente es un medio efectivo para reducir la PIM [44] Los mecanismos plausibles que generan dicho PIM incluyen las no linealidades de contacto metal-aislador-metal y metal-metal [45], particularmente debido a la topografía de la superficie en los contactos. Por ejemplo, se sabe que la alta fuerza aplicada a través de los contactos reduce la PIM. En las estaciones base celulares donde la potencia de las señales es muy alta, se sabe que es importante tener conexiones muy estrechas de cables que transporten señales de alta potencia.
La tunelación en un contacto metal-aislador-metal podría producir PIM. Se supone que esto es un problema particular con los contactos de aluminio-óxido-aluminio, ya que el espesor del óxido puede ser justo,\(2\text{ nm}\), para que se produzca un túnel [40, 45]. No obstante, se espera que este sea un contribuyente menor al PIM. Otra posible fuente de PIM es la emisión termiónica [46]. La emisión termiónica es secundaria a la tunelización y resultará en un pequeño aumento en la corriente de tunelización debido a otras fuentes [46].
El contacto metal a metal de metales diferentes actúa como un diodo débil debido a la diferencia en las funciones de trabajo de los metales. La alineación de los niveles de Fermi requiere carga para transferir del metal de alta función de trabajo al metal de baja función de trabajo. Dado que la transferencia de carga ha ocurrido entre los metales, por lo tanto existe un campo en la interfaz y por lo tanto hay un potencial de contacto. Se sabe que los contactos de cobre, plata y oro forman contactos bajos de PIM y estos metales tienen funciones de trabajo muy similares, lo que respalda la vista anterior. También en los contactos metal a metal hay una constricción del flujo de corriente debido a la topología de superficie rugosa que exagera el PIM debido al aumento de la densidad de corriente.
Los materiales ferromagnéticos como el hierro, el acero, el cobalto y el níquel producen PIM de alta significación [47]. Esto también es cierto para los materiales ferroeléctricos y piezoeléctricos.
4.7.2 Resumen
Existen muchas fuentes posibles de PIM, y siempre que se tenga cuidado para evitar metales disímiles y evitar materiales ferromagnéticos, la única fuente confirmada de PIM RF es el efecto de autocalentamiento electrotérmico [35, 37]. Sin embargo, no siempre es posible construir tales componentes ya que los requisitos mecánicos, eléctricos y de empaque deseables requieren el uso de elementos diferentes. Los metales ferromagnéticos como el níquel, un material de procesamiento deseable, producen PIM significativo. Con materiales no magnéticos disímiles hay claramente otra fuente (desconocida) de PIM a altas distancias de tono. Incluso con componentes cuidadosamente diseñados, el PIM existe en grandes espaciamientos de tono, y la fuente principal de PIM en estas circunstancias aún no ha sido identificada. Existe una confianza razonable de que dicho PIM es una no linealidad de corriente y no una no linealidad de voltaje [44]. Por lo que una estrategia para reducir la PIM es evitar altas densidades de corriente, y para el PIM electrotérmico, proporcionar una rápida disipación del calor lo más cerca posible de la fuente de calor. Otras fuentes de respuestas similares a PIM, es decir, distorsión de RF donde no se espera, se han encontrado debido a la vibración [48, 49] y la respuesta transitoria de un filtro [41, 42].

