5.3: Estudio de caso - Resonador sintonizable con pila de diodos varactores

Los varactores proporcionan una capacitancia sintonizable con el voltaje de polarización a través del varactor, un diodo polarizado inverso, cambiando la capacitancia del diodo. El voltaje de polarización aplicado también cambia la resistencia en serie del diodo, ver Figura 5.2.1. Las características de un varactor de microondas se muestran en la Figura\(\PageIndex{1}\). A una tensión de polarización inversa,\(V_{R} = 1\text{ V}\) la capacitancia de la unión\(C_{j} = 7\text{ pF}\) y la resistencia en serie es\(1.8\:\Omega\). En\(5\text{ GHz}\) la impedancia del diodo\(Z_{D}(1\text{ V})=1.8 −\jmath 4.54\:\Omega\) y su\(Q(1\text{ V})=2.5\). A una tensión de polarización inversa\(V_{R} = 10\text{ V}\), la capacitancia\(iC_{j} = 1\text{ pF}\) de la unión y la resistencia en serie es\(0.4\:\Omega\). En\(5\text{ GHz}\) la impedancia del diodo\(Z_{D}(1\text{ V})=0.4 −\jmath 31.8\:\Omega\) y su\(Q(1\text{ V}) = 80\).

Generalmente, un diseño procede basándose en una impedancia de sistema elegida que a menudo es\(50\:\Omega\) tal que el espacio de diseño incluye impedancias realizables por encima y por debajo de una impedancia del sistema. Una forma de aumentar efectivamente la impedancia de un diodo varactor es apilar diodos. Esto se muestra en la Figura\(\PageIndex{2}\) donde cuatro

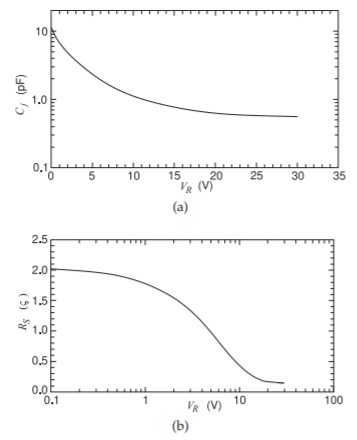
Figura\(\PageIndex{1}\): Características de un diodo varactor (Toshiba modelo JDV2S71E1, un diodo plano epitaxial de silicio) en función del voltaje de polarización inversa\(V_{R}\): (a) capacitancia\(C_{j}\); y (b) resistencia en serie\(R_{S}\).

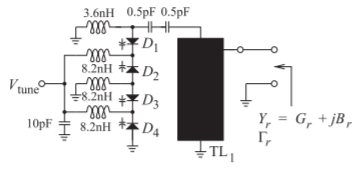
Figura\(\PageIndex{2}\): Un resonador de pila de diodos con carga corta diseñado para producir una capacitancia variable en el\(4–6\text{ GHz}\) rango. El elemento etiquetado TL1 es una línea de microcinta de baja impedancia. El inductor de choque,\(L_{\text{CHOKE}} = 8.2\text{ nH}\), presenta un circuito abierto de RF y es parte del circuito de polarización. Cada diodo varactor\((D_{1}–D_{4})\) es el modelo JDS2S71E.

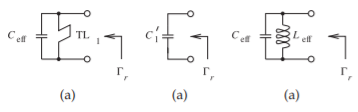
Figura\(\PageIndex{3}\): Circuitos equivalentes del resonador de pila de diodos stubloaded de la Figura\(\PageIndex{2}\).

\(D_{1},\ldots ,D_{4}\)Los diodos varactores se muestran junto con la disposición de polarización para que cada uno de los diodos se pueda ajustar mediante el voltaje de sintonización único\(V_{\text{tune}}\) aplicado a través de los inductores\(3.6\text{ nH}\) y de\(8.2\text{ nH}\) choque. Los inductores de choque proporcionan un cortocircuito de CC y un RF abierto (en realidad una magnitud de impedancia de\(258\:\Omega\) para el\(8.2\text{ nH}\) inductor en\(5\text{ GHz}\)). La figura\(\PageIndex{2}\) es el esquema de un resonador sintonizable, utilizado entre\(4\) y\(5.3\text{ GHz}\) para sintonizar un oscilador, ver [9] y Sección 5.6 de [10].

Los dos\(0.5\text{ pF}\) condensadores en la Figura\(\PageIndex{2}\) escalan la capacitancia de la pila de diodos y aumentan la efectividad\(Q\) de la capacitancia variable. La línea de transmisión en cortocircuito presenta una impedancia de inductancia en derivación con la pila de diodos aumentada. Aquí no se usa un inductor agrupado ya que tendría una pérdida demasiado alta. El circuito equivalente del resonador se muestra en la Figura\(\PageIndex{3}\). La red de resonadores está diseñada para ser resonante a una frecuencia superior a la frecuencia de operación. A la frecuencia de oscilación la red resonadora debe presentar una inductancia para resonar con la capacitancia del dispositivo activo en un oscilador. Además, para la estabilidad del oscilador, la inductancia efectiva debe tener una derivada particular de la admitancia con respecto a la frecuencia.

Los dos\(0.5\text{ pF}\) condensadores entre TL1 y la pila de varactores se combinan para proporcionar una capacitancia efectiva de la\(0.25\text{ pF}\) cual tiene una impedancia de\(127\:\Omega\) at\(5\text{ GHz}\). Entonces no es un condensador de bloqueo de CC que tendría una impedancia muy baja a RF, pero sí bloquea CC para que no\(V_{\text{tune}}\) se cortocircuite a tierra a través de la línea de transmisión. La función RF de los dos\(0.5\text{ pF}\) condensadores en serie es reducir el valor de la capacitancia variable, aumentar la reactancia operativa y aumentar\(Q\) la capacitancia efectiva. Cada diodo varactor tiene una\(0\text{ V}\) capacitancia de\(11\text{ pF}\) y una capacitancia a\(9\text{ V}\) de\(2.15\text{ pF}\). Con los cuatro varactores en serie esto se convierte en capacitancia\(2.75\text{ pF}\) total en\(0\text{ V}\) y\(0.54\text{ pF}\) en\(9\text{ V}\). La\(0.25\text{ pF}\) capacitancia en serie reduce esto a\(0.229\text{ pF}\) voltaje de\(0\text{ V}\) sintonización y\(0.171\text{ pF}\) a voltaje de\(9\text{ V}\) sintonización para una relación de sintonización de capacitancia de\(0.229\text{ pF}/0.171\text{ pF} = 1.34\). El rango de sintonización de capacitancia se ha reducido de la relación original de\(2.75\text{ pF}/ 0.54\text{ pf} = 5.05\). El rango de sintonización de la frecuencia resonante de un\(LC\) resonador paralelo es la raíz cuadrada de este, es decir\(1.16\) (que proviene de la frecuencia resonante que es\(1/\sqrt{LC}\)). Si esto no es suficiente, los dos\(0.5\text{ pF}\) condensadores se pueden cambiar para lograr la relación de sintonización de capacitancia general requerida.

El\(10\text{ pF}\) condensador entre el\(V_{\text{tune}}\) terminal y la tierra está ahí para asegurar un cortocircuito de RF. La magnitud si la impedancia de este condensador en\(5\text{ GHz}\) es\(3.2\:\Omega\), un factor de diez lejos de la impedancia\(50\:\Omega\) del sistema. Mientras que en RF el terminal at\(V_{\text{tune}}\) es idealmente un cortocircuito a tierra, siempre habrá alguna inductancia de cableado.

Las características del resonador se pueden entender observando la gráfica del coeficiente de reflexión simulado del resonador\(\Gamma_{\Gamma}\), en una gráfica de Smith, ver Figura\(\PageIndex{4}\). \(\Gamma_{\Gamma}\)se muestra para dos voltajes de sintonización así como el locus del dispositivo de la inversa del coeficiente de reflexión de entrada de un circuito transistor

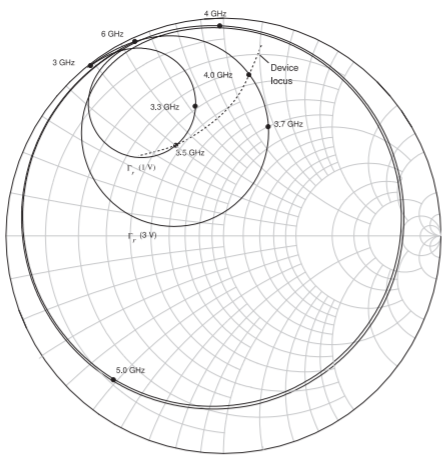
Figura\(\PageIndex{4}\): Coeficiente de reflexión simulada del resonador,\(\Gamma_{\Gamma}\) en una gráfica\(50\:\Omega\) Smith para dos voltajes de sintonización (\(1\text{ V}\)y\(3\text{ V}\)). El locus de accionamiento mostrado es el inverso del coeficiente de reflexión de entrada de una red activa que estaría conectada en el mismo puerto que para\(\Gamma_{\Gamma}\). La intersección\(\Gamma_{\Gamma}\) y el lugar de accionamiento determina la frecuencia de operación.

conectado al resonador. La combinación del resonador y el dispositivo activo forma un oscilador. La intersección del dispositivo activo y los loci del resonador selecciona la frecuencia de oscilación del oscilador. El oscilador presenta una capacitancia al resonador y por lo tanto el resonador debe presentar una inductancia al dispositivo activo. La frecuencia del oscilador se varía cambiando\(\Gamma_{\Gamma}\) el resonador

En la Figura se muestra una fotografía del resonador\(\PageIndex{5}\). La medida\(\Gamma_{\Gamma}\) se muestra en la Figura\(\PageIndex{6}\) y esto corresponde a la gráfica simulada en la Figura\(\PageIndex{4}\). Las dos parcelas están aproximadamente de acuerdo pero hay una discrepancia porque es muy difícil hacer estas mediciones en\(5\text{ GHz}\), y los modelos de los componentes del dispositivo no son exactos. Sin embargo, la razón principal de la discrepancia es que se trata de una medición de un circuito resonante y pequeñas discontinuidades pueden tener un efecto dramático. Lo que aquí se presenta es típico del diseño de circuitos de microondas y por qué se requiere una tremenda intuición para diseñar a frecuencias de microondas e interpretar mediciones.

Figura\(\PageIndex{5}\): Fotografía de la red de resonadores de microcinta con componentes de montaje en superficie. La barra de cortocircuito es una resistencia de montaje en\(0\:\Omega\) superficie y se utiliza para ajustar la longitud efectiva del resonador de línea de transmisión,\(\text{TL}_{1}\).

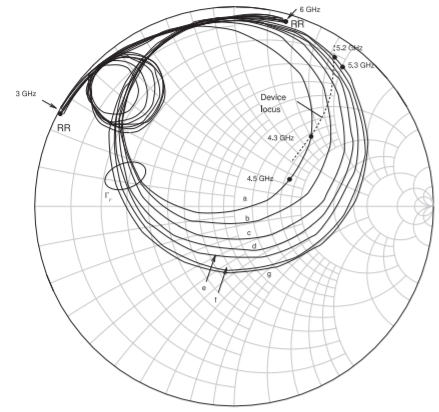
Figura\(\PageIndex{6}\): Coeficiente de reflexión medido de la red resonadora,\(\Gamma_{\Gamma}\). Curva\(a\), es la característica de la red de resonadores para un voltaje de sintonización,\(V_{\text{tune}}\), de\(0\text{ V}\). La curva\(g\) es para\(V_{\text{tune}} = 9\text{ V}\). \(V_{\text{tune}}\)está igualmente espaciado para Curvas\(a– g\). Se muestra la inversa del coeficiente de reflexión de un dispositivo activo conectado en el\(\Gamma_{\Gamma}\) punto e indica que el dispositivo activo presenta una conductancia negativa. La intersección del locus del dispositivo y\(\Gamma_{\Gamma}\) determina la frecuencia de oscilación de un oscilador. Así ajustando\(V_{\text{tune}}\) cambia la frecuencia de oscilación.