5.4: Conmutador
- Page ID
- 85260
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Los interruptores de microondas se utilizan comúnmente para conectar alternativamente una antena a un transmisor o un receptor. En algunos sistemas de comunicación, como el GSM y algunos modos de 4G y 5G, un teléfono no transmite y recibe simultáneamente. En consecuencia, se puede usar un conmutador para separar las señales transmitidas y recibidas. En los teléfonos multibanda, se utiliza un interruptor para conectar el transmisor y receptor correctos, que son específicos de banda, a la antena. En los sistemas de radar, los interruptores se utilizan para dirigir un haz de antena cambiando la fase de la señal de microondas entregada a cada antena en una matriz de antenas. Un interruptor de microondas ideal se muestra en la Figura\(\PageIndex{1}\) (a), donde se muestran un puerto de entrada y un puerto de salida.\(\text{RF}_{\text{IN}}\)\(\text{RF}_{\text{OUT}}\) Para una transferencia de potencia máxima entre los puertos, el switch debe tener poca pérdida y por lo tanto tener baja resistencia. A frecuencias de microondas, los interruptores realistas deben modelarse con parásitos y con resistencias finitas de encendido y apagado. En la Figura\(\PageIndex{1}\) (b) se muestra un modelo realista aplicable a muchos tipos de interruptores. Los parásitos capacitivos, los\(C_{P}\) s, limitan la frecuencia de operación de los interruptores y la resistencia on,\(R_{\text{ON}}\), impacta la pérdida del interruptor. Idealmente la resistencia fuera,\(R_{\text{OFF}}\), es muy grande, sin embargo, la capacitancia de derivación parásita\(C_{\text{OFF}}\),, es casi siempre más significativa. El resultado es que a altas frecuencias existe una conexión capacitiva alternativa entre la entrada y la salida a través de\(C_{\text{OFF}}\). La resistencia on del interruptor introduce división de voltaje que se puede ver comparando la conexión ideal mostrada en la Figura\(\PageIndex{1}\) (c) y la conexión más realista mostrada en la Figura\(\PageIndex{1}\) (d). A partir de la relación de división de voltaje, se puede calcular la pérdida del interruptor.
Los conmutadores están configurados para proporcionar conexiones desde una o más entradas a una o más salidas. La configuración de un interruptor está indicada por polos y tiros, y varias configuraciones se muestran en la Figura\(\PageIndex{2}\). En aplicaciones de microondas, los interruptores unipolares son los más utilizados y la entrada está conectada a una antena. Por ejemplo, los lanzamientos estarían conectados a diferentes bandas de un teléfono multibanda.
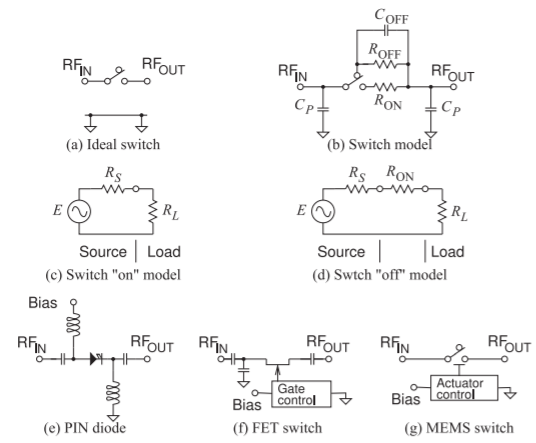
Figura\(\PageIndex{1}\): Interruptores de microondas: (a) conexión de interruptor ideal\(\text{RF}_{\text{IN}}\) y\(\text{RF}_{\text{OUT}}\) puertos; (b) modelo de un interruptor de microondas; (c) modelo de circuito ideal con interruptor encendido y con fuente y carga; (d) modelo de circuito de baja frecuencia realista con el interruptor encendido; (e) interruptor realizado usando un diodo PIN; (f) interruptor realizado usando un FET; y (g) interruptor realizado usando un interruptor MEMS.
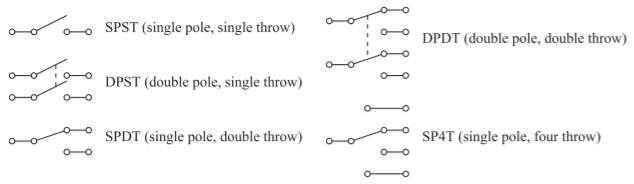
Figura\(\PageIndex{2}\): Configuraciones de conmutador.
| Tipo de interruptor | Configuración | Manejo de potencia | Máxima pérdida de inserción | Frecuencia de funcionamiento | Voltaje de accionamiento | Tiempo de respuesta |
|---|---|---|---|---|---|---|
| MEMS\(^{1}\) | SPDT | \(0.5\text{ W}\) | \(0.5\text{ dB}\) | a\(10\text{ GHz}\) | \(90\text{ V}\) | \(10\:\mu\text{s}\) |
| MEMS\(^{1}\) | SPDT | \(4\text{ W}\) | \(0.8\text{ dB}\) | a\(35\text{ GHz}\) | \(110\text{ V}\) | \(10\:\mu\text{s}\) |
| FET (PhEMT)\(^{2}\) | SPDT | \(10\text{ W}\) | \(0.3\text{ dB}\) | a\(6.5\text{ GHz}\) | \(5\text{ V}\) | \(0.5\:\mu\text{s}\) |
| FET (PhEMT)\(^{2}\) | SPDT | \(0.3\text{ W}\) | \(1.1\text{ dB}\) | a\(25\text{ GHz}\) | \(5\text{ V}\) | \(0.5\:\mu\text{s}\) |
| PIN\(^{3}\) | SPDT | \(13\text{ W}\) | \(0.35\text{ dB}\) | a\(2\text{ GHz}\) | \(12\text{ V}\) | \(0.5\:\mu\text{s}\) |
| PIN\(^{3}\) | SPDT | \(10\text{ W}\) | \(0.4\text{ dB}\) | a\(6\text{ GHz}\) | \(12\text{ V}\) | \(0.5\:\mu\text{s}\) |
| FET (SOI)\(^{4}\) | SPDT | \(2\text{ W}\) | \(2.7\text{ dB}\) | a\(60\text{ GHz}\) | \(3.6\text{ V}\) | \(8\text{ ns}\) |
Tabla\(\PageIndex{1}\): Propiedades típicas de pequeños interruptores de microondas. (Fuentes:\(^{1}\) Radant MEMS,\(^{2}\) RF Micro Devices,\(^{3}\) Tyco Electronics y\(^{2}\) PSemi\(^{\text{TM}}\) Corporation.)
Hay cuatro tipos principales de interruptores de microondas: mecánicos, diodos PIN, FET e interruptores de sistema microelectromecánico (MEMS). Los interruptores mecánicos son casi sin pérdidas, pero tienden a ser grandes, relativamente caros, lentos de operar y se utilizan principalmente en entornos de laboratorio. Los otros conmutadores son de mayor interés para su uso en sistemas. Los conmutadores de diodo PIN, FET y MEMS se muestran en las Figuras\(\PageIndex{1}\) (e—g), respectivamente. Con estas tecnologías, la mayoría de los switches de orden superior se basan en interconexiones de conmutadores SPST. Los atributos de estos conmutadores se resumen en Tabla\(\PageIndex{1}\) para conmutadores que son adecuados para aplicaciones de teléfonos celulares. Los interruptores de diodo PIN son los más robustos, manejan la mayor potencia de RF y funcionan a frecuencias más altas que los conmutadores basados en FET o MEMS. No obstante, esto tiene un precio. El diodo PIN utilizado es similar a un diodo de unión pn con la adición de una capa intrínseca entre los materiales de tipo p y n. Con polarización directa aplicada, el diodo tiene baja resistencia de la serie RF. En polarización inversa, la resistencia de RF del diodo es grande. La polarización directa requiere corriente y voltaje CC, por lo que la energía de control se consume cuando un interruptor de diodo PIN está encendido. La configuración del circuito para un interruptor de diodo PIN SPST se muestra en la Figura\(\PageIndex{1}\) (e). Se requieren condensadores de desacoplamiento de sesgo en serie en los puertos de RF.
Un FET hace un buen interruptor electrónico; con el sesgo correcto aplicado a la puerta, la conexión drenaje-fuente parece una resistencia pequeña. Cambiar el sesgo al otro extremo elimina los portadores libres del canal entre el drenaje y la fuente, y el resultado es una gran resistencia. Tanto Si como GaAs
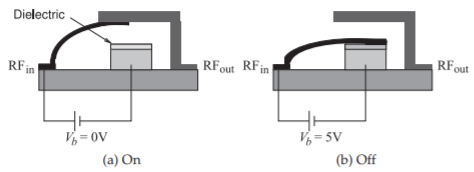
Figura\(\PageIndex{3}\): Interruptor RF MEMS: (a) la\(_{\text{in}}\) línea de RF en contacto con la\(_{\text{out}}\) línea de RF; y (b) el haz de cantlever atraído electrostáticamente al pedestal y no hay conexión RF.
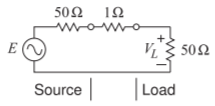
Figura\(\PageIndex{4}\): Modelo utilizado en el cálculo de la pérdida de un interruptor en un\(50\:\Omega\) sistema.
los interruptores se utilizan en teléfonos celulares, con interruptores GaAs que operan a frecuencias extendidas acercándose\(6\text{ GHz}\). El funcionamiento de un FET se puede describir como una resistencia variable drenaje-fuente con la tensión puerta-fuente controlando la sección transversal del canal. El circuito para un interruptor SPST basado en FET se muestra en la Figura\(\PageIndex{1}\) (f). Se requieren capacitores de bloqueo de sesgo en serie en los puertos de RF. La alimentación de control solo se requiere para cambiar el estado del interruptor; se requiere una potencia insignificante para mantener el estado del interruptor.
Un interruptor MEMS se fabrica utilizando técnicas fotolitográficas similares a las utilizadas en la fabricación de semiconductores [11, 12, 13]. Se trata esencialmente de interruptores mecánicos en miniatura con una tensión utilizada para controlar la posición de un brazo de cortocircuito, que suele ser un voladizo o una membrana, ver Figura\(\PageIndex{3}\). Como no hay conexión directa entre la ruta de la señal de RF y los circuitos de control, los conmutadores MEMS tienen frecuencias de funcionamiento inherentemente altas. Se requiere alimentación para cambiar el interruptor, pero una vez que se ha logrado la conmutación, se requiere una alimentación de CC insignificante para mantener la conexión. Dos de los principales problemas son crear el contacto con suficiente fuerza para reducir la resistencia en serie, y mantener la integridad estructural de los contactos después de cientos de millones de ciclos. Generalmente no es necesario hacer un contacto de CC, y crear una estructura que tenga una gran diferencia entre la capacitancia on y off capacitancia es suficiente para aplicaciones como redes de correspondencia sintonizables [11].
Ejemplo\(\PageIndex{1}\): Insertion Loss of a Switch
¿Cuál es la pérdida de inserción de un interruptor con una resistencia de\(1\:\Omega\) encendido cuando se usa en un\(50\:\Omega\) sistema?
Solución
El modelo que se utilizará para evaluar la pérdida de inserción del interruptor se muestra en la Figura\(\PageIndex{4}\). La pérdida de inserción se encuentra determinando primero la potencia disponible de la fuente y luego la potencia real entregada a la carga. La potencia de entrada disponible se calcula ignorando primero la resistencia del\(1\:\Omega\) interruptor. Luego hay una transferencia máxima de potencia desde la fuente a la carga. La potencia de entrada disponible es
\[\label{eq:1}P_{Ai}=\frac{1}{2}\frac{\left(\frac{1}{2}E\right)^{2}}{50}=\frac{E^{2}}{400} \]
donde\(E\) es el voltaje pico de RF en el generador de fuente equivalente Thevenin. La potencia entregada a la\(50\:\Omega\) carga se encuentra después de determinar primero el voltaje de carga pico:
\[\label{eq:2}V_{L}=\frac{50}{50+1+50}E=\frac{50}{101}E \]
Por lo tanto, la potencia entregada a la carga es
\[\label{eq:3}P_{D}=\frac{1}{2}\frac{V_{L}^{2}}{50}=\frac{1}{100}\left(\frac{50}{101}\right)^{2}E^{2} \]
La pérdida de inserción es
\[\label{eq:4}\text{IL}=\frac{P_{Ai}}{P_{D}}=\frac{E^{2}}{400}\frac{100}{E^{2}}\left(\frac{101}{50}\right)^{2}=1.020=0.086\text{ dB} \]


