7.2: Distorsión no lineal de un sistema en cascada
- Page ID
- 85193
Esta sección se basa en el análisis de distorsión de redes de dos puertos en la Sección 4.5 y aborda la determinación de las métricas no lineales de un sistema en cascada como el receptor que se muestra en la Figura 7.1.2. Los filtros y las redes de coincidencia entre etapas eliminan los armónicos del sistema pero, desafortunadamente, permiten que los componentes de distorsión dentro de banda y fuera de banda pasen a través del sistema. Las principales métricas que describen el rendimiento no lineal son los niveles de potencia en el punto de compresión de\(1\text{ dB}\) ganancia y en el punto de intercepción (\(\text{IP3}\)) de tercer orden. En algunos sistemas, como los receptores de conversión directa, también es importante el punto de intercepción de segundo orden (\(\text{IP2}\)). Estas métricas se relacionan con tonos discretos y la distorsión correlacionada generada en las diferentes etapas. Esto contrasta con el cálculo del ruido de un sistema en cascada donde el ruido agregado por etapas no está correlacionado.
7.2.1 Compresión de ganancia en un sistema en cascada
Cuando se conectan en cascada dos etapas de amplificador es necesario determinar el punto de compresión de\(1\text{ dB}\) ganancia de la cascada. Considera la cascada en la Figura\(\PageIndex{1}\). Las dos etapas tienen ganancias lineales de potencia\(G_{1}\) y\(G_{2}\), y puntos\(1\text{ dB}\) de compresión\(P_{1, 1\text{ dB}}\) y\(P_{2,1 \text{dB}}\), respectivamente. La ganancia de potencia lineal total del sistema es\(G^{T} = G_{1}\cdot G_{2}\). Si la expansión de la serie Taylor de las características de entrada-salida de la primera etapa en la cascada es
\[\label{eq:1}v_{1o}(t)=a_{0}+a_{1}v_{1i}(t)+a_{2}v_{1i}^{2}(t)+a_{3}v_{1i}^{3}(t)+\ldots \]
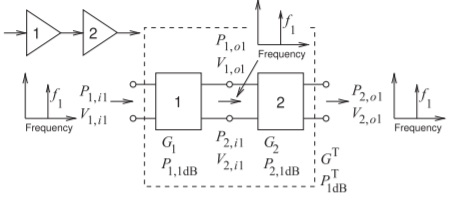
Figura\(\PageIndex{1}\): Cascada de dos etapas utilizadas para determinar el punto de\(1\text{ dB}\) compresión total del sistema.
entonces en la interfaz de las dos etapas la amplitud del tono a\(f_{1}\) debido a una entrada de un solo tono,\(v_{i}(t) = V_{i} \cos(\omega_{1}t)\), es\(v_{1o}(t) = V_{1o} \cos(\omega_{1}t)\), donde
\[\label{eq:2}V_{1o}=a_{1}V_{i}+\frac{3}{4}a_{3}V_{i}^{3} \]
Los armónicos son ignorados, ya que el diseño de la red de emparejamiento entre etapas sería preferiblemente de paso bajo para eliminar el paso de armónicos. El insumo de la segunda etapa es\(v_{2i}(t) = v_{1o}(t)\), siendo la expansión de la serie Taylor de la segunda etapa
\[\label{eq:3}v_{2o}(t)=b_{o}+b_{1}v_{2i}(t)+b_{2}v_{2i}^{2}(t)+b_{3}v_{1i}^{3}(t)+\ldots \]
Por lo tanto, el componente de la salida final en\(f_{1}\) será
\[\label{eq:4}V_{o}=a_{1}b_{1}V_{i}+\frac{3}{4}b_{1}a_{3}V_{i}^{3}+\frac{3}{4}a_{1}b_{3}V_{i}^{3}+\ldots \]
Es decir, la señal de entrada se multiplica por la ganancia lineal general del amplificador; este es el primer término a la derecha en Ecuación\(\eqref{eq:4}\), y los dos últimos términos dan como resultado compresión de ganancia. Si las etapas son idénticas (es decir,\(a_{1} = b_{1}\) y\(a_{3} = b_{3}\)) los dos términos de compresión de ganancia serán idénticos. Así las dos etapas contribuirán por igual a ganar compresión.
Tenga en cuenta que en Ecuación se suman\(\eqref{eq:4}\) los voltajes para producir la compresión de ganancia global. En general las dos etapas no serán idénticas, tendrán diferentes puntos de ganancia y\(1\text{ dB}\) compresión, sin embargo, esta observación (es decir, que se suman los voltajes) sí permite desarrollar una expresión aproximada para el punto de\(1\text{ dB}\) compresión de un sistema en cascada.
El examen de la ecuación\(\eqref{eq:4}\) conduce a una fórmula general para el punto de\(1\text{ dB}\) compresión total,\(P_{1\text{dB}}^{T}\), de la cascada de dos etapas en la Figura\(\PageIndex{1}\):
\[\label{eq:5}(P_{1\text{dB}}^{T})^{-\frac{1}{2}}\approx (G_{2}P_{1,1\text{ dB}})^{-\frac{1}{2}}+(P_{2,1\text{ dB}})^{-\frac{1}{2}} \]
Obsérvese que aquí las ganancias y los poderes son cantidades absolutas y no en decibelios. Por ejemplo,\(P_{1\text{dB}}^{T}\) es la potencia en vatios en el punto de compresión de\(1\text{ dB}\) ganancia.
\(\eqref{eq:5}\)La ecuación es una estimación muy conservadora del punto de compresión de\(1\text{ dB}\) ganancia del amplificador y señala los niveles de potencia más bajos a los que podría ocurrir la compresión de ganancia de la cascada. La situación podría ser mejor dependiendo de la fase de los componentes de distorsión, pero el conservadurismo es muy importante en el diseño del sistema. El peor de los casos es lo que importa al especificar el rendimiento del sistema. Obtener el efecto de la fase correctamente en el diseño del sistema requiere una simulación a nivel de circuito, pero cuando se trabaja con módulos, dicha información rara vez está disponible. La ecuación\(\eqref{eq:5}\) no puede derivarse directamente de la expansión de voltaje, ya que la ganancia de potencia de los amplificadores de microondas se debe a la diferencia de los niveles de impedancia de entrada y salida además de la ganancia de voltaje. Cabe señalar que un amplificador de microondas se desvía de la linealidad siguiendo una respuesta más nítida, similar al tanh, que la descrita por un modelo polinómico de orden bajo de linealidad. Por lo tanto, la simple cascada de polinomios de orden bajo que describen cada etapa no es una opción viable.
Si es necesario y si se requiere una estimación más realista y puede justificarse, entonces una fórmula menos conservadora que pueda usarse para estimar el nivel de compresión de ganancia de dos etapas en cascada es
\[\label{eq:6}(P_{1\text{ dB}}^{T})^{-1}\approx (G_{2}P_{1,1\text{ dB}})^{-1}+(P_{2,1\text{ dB}})^{-1} \]
Por lo general, es mejor usar la estimación más conservadora de compresión en Ecuación\(\eqref{eq:5}\).
Ejemplo\(\PageIndex{1}\): Gain Compression of a Two-Stage Amplifier
La primera etapa de un amplificador de dos etapas en un transmisor tiene una ganancia\(G_{1} = 20\text{ dB}\) y una potencia de compresión de\(1\text{ dB}\) ganancia de salida\(P_{1,1\text{ dB}} = 10\text{ dBm}\). La segunda etapa tiene una ganancia\(G_{2} = 6\text{ dB}\) y una potencia de compresión de\(1\text{ dB}\) ganancia de salida\(P_{2,1\text{ dB}} = 20\text{ dBm}\).
- ¿Cuál es la ganancia lineal del amplificador de dos etapas?
- ¿Cuál es la ganancia del amplificador de dos etapas en la potencia de compresión de\(1\text{ dB}\) ganancia?
- ¿Cuál es la potencia de compresión de\(1\text{ dB}\) ganancia del sistema en cascada?
Solución
- Cuando la ganancia de una etapa amplificadora se da sin calificación se debe suponer que es la ganancia lineal, es decir, la ganancia a niveles de señal pequeños. Entonces, la ganancia de potencia lineal total del amplificador de dos etapas es
\[G^{T}=G_{1}G_{2}=20\text{ dB}+6\text{ dB}=26\text{ dB}\nonumber \] - La ganancia comprimida será\(1\text{ dB}\) menor, es decir,\(G^{T} = 25\text{ dB}\).
- La potencia de compresión de ganancia global,\(P^{T}_{1\text{ dB}}\) se obtiene aproximadamente usando la Ecuación\(\eqref{eq:5}\):
\[\begin{align}\left(P_{1\text{ dB}}^{T}\right)^{-\frac{1}{2}}&=(G_{2}P_{1,1\text{ dB}})^{-\frac{1}{2}}+(P_{2,1\text{ dB}})^{-\frac{1}{2}} = \left(10^{(6/10)}10^{(10/10)}\right)^{-\frac{1}{2}}+\left(10^{(20/10)}\right)^{-\frac{1}{2}}\nonumber\\ \label{eq:7}P_{1\text{ dB}}^{T}&=\left[(3.981\cdot 10)^{-\frac{1}{2}}+(100)^{-\frac{1}{2}}\right]^{-2}\text{ mW}=14.97\text{ mW}=11.8\text{ dBm}\end{align} \]
Una comprobación rápida es la siguiente.
Si Stage\(1\) domina la compresión de ganancia, la potencia de salida en la\(1\text{ dB}\) compresión se\(P_{1,1\text{ dB}} = 10\text{ dBm}\) multiplica por la ganancia de potencia lineal de la segunda etapa, es decir,\(P^{T}_{1\text{ dB}} = G_{2}P_{1,1\text{ dB}} = 6\text{ dB} + 10\text{ dBm} = 16\text{ dBm}\).
Si Stage\(2\) domina la compresión, la potencia de salida a la\(1\text{ dB}\) compresión del amplificador de dos etapas es solo la de Etapa\(2\):\(P^{T}_{1\text{ dB}} = 20\text{ dBm}\).
Ejemplo\(\PageIndex{2}\): Second Example of Gain Compression of a Two-Stage Amplifier
La primera etapa de un amplificador de dos etapas en un transmisor tiene una ganancia\(G_{1} = 13\text{ dB}\) y una potencia de compresión de\(1\text{ dB}\) ganancia de salida\(P_{1,1\text{ dB}} = 10\text{ dBm}\). La ganancia de la segunda etapa es\(G_{2} = 10\text{ dB}\) y la potencia de compresión de\(1\text{ dB}\) ganancia de salida es\(P_{2,1\text{ dB}} = 20\text{ dBm}\). ¿Cuál es la potencia de compresión de\(1\text{ dB}\) ganancia del sistema amplificador de dos etapas?
Solución
La potencia de compresión de ganancia total,\(P^{T}_{1\text{ dB}}\), se obtiene aproximadamente usando la ecuación\(\eqref{eq:5}\):
\[\begin{align}\left(P_{1\text{ dB}}^{T}\right)^{-\frac{1}{2}}&=(G_{2}P_{1,1\text{ dB}})^{-\frac{1}{2}}+(P_{2,1\text{ dB}})^{-\frac{1}{2}} = \left(10^{\frac{10}{10}}10^{\frac{10}{10}}\right)^{-\frac{1}{2}}+\left(10^{\frac{20}{10}}\right)^{-\frac{1}{2}}\quad \text{(mW)}^{-\frac{1}{2}} \nonumber\\ \label{eq:8}P_{1\text{ dB}}^{T}&=\left[(100)^{-\frac{1}{2}}+(100)^{-\frac{1}{2}}\right]^{-2}\text{ mW}=25.00\text{ mW}=13.98\text{ dBm}\end{align} \]
Una comprobación rápida es la siguiente.
Si Stage\(1\) domina la compresión, la potencia de salida a la\(1\text{ dB}\) compresión del amplificador de dos etapas se\(P_{1,1\text{ dB}}\) multiplica por la ganancia de potencia lineal de la segunda etapa, taht es\(P^{T}_{1\text{ dB}} = G_{2}P_{1,1\text{ dB}} = 10\text{ dBm} + 10\text{ dB} = 20\text{ dBm}\).
Si Stage\(2\) domina la compresión,\(P^{T}_{1\text{ dB}} = P_{2,1\text{ dB}} = 20\text{ dBm}\). Por lo tanto, ninguna etapa domina la compresión.
Una nota final es que el cálculo del punto de\(1\text{ dB}\) compresión cuando ambas etapas en un sistema de dos etapas contribuyen por igual a la compresión de ganancia es aproximado ya que la característica de compresión real es compleja y una serie Taylor de tercer orden no captura la respuesta no lineal total [1, 2].
La respuesta de un sistema multietapa se puede extrapolar del tratamiento aquí para dos etapas. Para una cascada\(m\) de etapa,
\[\label{eq:9}\left(P_{1\text{ dB}}^{T}\right)^{-\frac{1}{2}}=(G_{m}\ldots G_{2}P_{1,1\text{ dB}})^{-\frac{1}{2}}+\ldots +\left(G_{2}P_{(m-1),1\text{ dB}}\right)^{-\frac{1}{2}}+(P_{m,1\text{ dB}})^{-\frac{1}{2}} \]
7.2.2 Distorsión de intermodulación en un sistema en cascada
El sistema de dos etapas mostrado en la Figura se\(\PageIndex{2}\) utilizará aquí para determinar la respuesta de intermodulación total como se describe por los puntos de intercepción de entrada y salida de tercer orden,\(\text{IIP3}\) y\(\text{OIP3}\), respectivamente. El desarrollo se basa en el análisis de distorsión de intermodulación en la Sección 4.5.3 y se denomina método de intercepción en cascada. Una versión del método se llama el método de intercepción en cascada organizada, en el que la peor situación
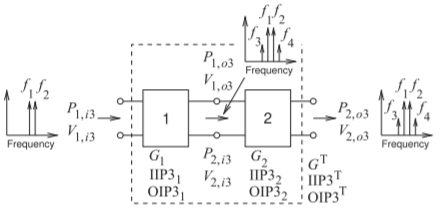
Figura\(\PageIndex{2}\): Cascada de dos etapas utilizadas para determinar el punto de intercepción de tercer orden de un sistema en cascada.
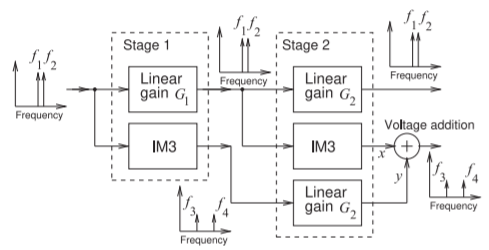
Figura\(\PageIndex{3}\): Flujo de señal para calcular la distorsión de intermodulación en cascada de dos etapas.
se supone, en que los\(\text{IM3}\) productos de cada etapa en la cascada se suman en fase. El otro método es el método de intercepción en cascada desorganizada en el que se desconocen las fases de\(\text{IM3}\) producción por cada etapa, y asume que la\(\text{IM3}\) distorsión general más probable se obtendrá asumiendo una relación de fase aleatoria de las\(\text{IM3}\) contribuciones.
El punto de intercepción de tercer orden\(\text{IP3}\),, se determina extrapolando la ganancia de señal pequeña y\(\text{IM3}\) las respuestas. Dado que\(\text{IM3}\) es pequeño, el flujo de señal en el sistema de dos etapas es como se muestra en la Figura\(\PageIndex{3}\). Una trayectoria en el flujo amplifica linealmente la señal de entrada de dos tonos en Etapas\(1\) y\(2\). La no linealidad de tercer orden de Stage\(1\) crea un nivel bajo\(\text{IM3}\) que se amplifica linealmente por la segunda etapa. Un segundo conjunto de\(\text{IM3}\) señales es producido por el\(\text{IM3}\) de la segunda etapa que opera sobre la señal de dos tonos amplificada por Stage\(1\). Los voltajes de las dos\(\text{IM3}\) señales se suman constructivamente. Una complicación es que no se conocen las fases de\(\text{IM3}\) las dos señales\(y\), at\(x\) y,. Esto lleva a dos enfoques para estimar la distorsión general.
Método de interceptación en cascada organizada
La peor situación es que los\(\text{IM3}\) voltajes en\(x\) y\(y\) están en fase para que los voltajes se sumen. Entonces se obtiene la\(\text{IM3}\) distorsión total sumando los voltajes IM3 generados de cada etapa. Determinar el total\(\text{OIP3}\),\(\text{OIP3}^{\text{T}}\) es el problema inverso. Esto no se puede resolver con precisión, pero\(\text{OIP3}^{\text{T}}\) se obtiene una buena estimación para [3, 4]
\[\label{eq:10}(\text{OIP3}^{\text{T}})^{-\frac{1}{2}}\approx (G_{2}\text{OIP3}_{1})^{-\frac{1}{2}}+(\text{OIP3}_{2})^{-\frac{1}{2}} \]
Tenga en cuenta que\(\text{OIP3}\) es un poder y\(G\) es una ganancia de poder. Ahora la ganancia total de la cascada\(G^{T} = G_{1}G_{2}\), y ya que\(\text{OIP3}^{\text{T}} = G^{T}\text{IIP3}^{\text{T}}\), donde\(\text{OIP3}^{\text{T}}\), la intercepción de entrada de la cascada, se puede escribir
\[\label{eq:11}(\text{IIP3}^{\text{T}})^{-\frac{1}{2}}\approx (\text{IIP3}_{1})^{-\frac{1}{2}}+(\text{IIP3}_{2}/G_{1})^{-\frac{1}{2}} \]
Generalizando estos resultados, para una cascada\(m\) -stage el general\(\text{OIP3}\) es
\[\begin{align}(\text{OIP3}^{\text{T}})^{-\frac{1}{2}}&\approx (G_{m}\ldots G_{2}\text{OIP3}_{1})^{-\frac{1}{2}}+\ldots \left(G_{m}\text{OIP3}_{(m-1)}\right)^{-\frac{1}{2}}\nonumber \\ \label{eq:12} &\quad +(\text{OIP3}_{m})^{-\frac{1}{2}}\end{align} \]
Ya que\(\text{IIP3} = \text{OIP3}/G\), el resultado general para múltiples etapas en cascada se puede escribir
\[\label{eq:13}\left(\frac{1}{\text{IIP3}^{\text{T}}}\right)^{\frac{1}{2}}\approx\left(\frac{1}{\text{IIP3}_{1}}\right)^{\frac{1}{2}}+\ldots \left(\frac{G_{(m-2)}\ldots G_{1}}{\text{IIP3}_{(m-1)}}\right)^{\frac{1}{2}}+\left(\frac{G_{(m-1)}\ldots G_{1}}{\text{IIP3}_{m}}\right)^{\frac{1}{2}} \]
El método de intercepción en cascada organizada a menudo proporciona una estimación\(\text{OIP3}^{\text{T}}\) y\(\text{IIP3}^{\text{T}}\) distorsión demasiado conservadora (es decir, demasiado baja).
Método de intercepción en cascada desorganizado
Si las fases de las etapas son aleatorias (o quizás desconocidas), entonces es razonable agregar los poderes de los términos de distorsión. Esta es una aproximación ya que las\(\text{IM3}\) señales aún están correlacionadas, pero se ha encontrado que este enfoque proporciona una medida útil en el diseño, entonces
\[\label{eq:14}(\text{OIP3}^{\text{T}})^{-1}\approx (G_{2}\text{OIP3}_{1})^{-1}+(\text{OIP3}_{2})^{-1} \]
y de nuevo\(\text{OIP3}\) es un poder y\(G\) es una ganancia de poder. Para una cascada\(m\) -etapa con\(\text{IM3}\) fase aleatoria el total\(\text{OIP3}\),\(\text{OIP3}^{\text{T}}\), se obtiene de
\[\label{eq:15}(\text{OIP3}^{\text{T}})^{-1}\approx (G_{m}\ldots G_{2}\text{OIP3}_{1})^{-1}+\ldots +(G_{2}\text{OIP3}_{(m-1)})^{-1}+(\text{OIP3}_{m})^{-1} \]
y el total\(\text{IIP3}\),\(\text{IIP3}^{\text{T}}\), se obtiene de (desde\(\text{IIP3} = \text{OIP3}/G)\)
\[\label{eq:16}\left(\frac{1}{\text{IIP3}^{\text{T}}}\right)\approx\left(\frac{1}{\text{IIP3}_{1}}\right)+\left(\frac{G_{1}}{\text{IIP3}_{2}}\right)+\ldots +\left(\frac{G_{(m-1)}\ldots G_{1}}{\text{IIP3}_{m}}\right) \]
Resumen
El método de intercepción en cascada ha dado lugar a dos conjuntos de resultados para la\(\text{IM3}\) distorsión. El primero, del método organizado de intercepción en cascada, es la peor situación en la que la\(\text{IM3}\) distorsión de cada etapa se combina de la peor manera posible. Esto arrojó el general\(\text{IIP3}\) y\(\text{OIP3}\) los resultados de Ecuaciones\(\eqref{eq:12}\) y\(\eqref{eq:13}\). El segundo, a partir del método desorganizado de intercepción en cascada, supone que las fases de la\(\text{IM3}\) de cada etapa están relacionadas aleatoriamente, quizás la mejor estimación que se pueda hacer sin una simulación de circuito. Esto arrojó el general\(\text{IIP3}\) y\(\text{OIP3}\) los resultados de Ecuaciones\(\eqref{eq:15}\) y\(\eqref{eq:16}\).
Es interesante especular qué pasaría si las etapas se diseñaran de manera que las\(\text{IM3}\) contribuciones en\(x\) y\(y\) (refiriéndose a la Figura\(\PageIndex{3}\)) de la primera y segunda etapas estuvieran\(180^{\circ}\) fuera de fase pero con la misma magnitud. Si esto pudiera hacerse las\(\text{IM3}\) contribuciones a la salida serían canceladas. En efecto, es posible hacerlo de manera limitada. La fase de las\(\text{IM3}\) señales depende del nivel de la señal y por lo tanto cambia sobre el rango de la señal. Un diseño cuidadoso, y solo cuando existe un control completo sobre el diseño e integración de las etapas, permite que las contribuciones IMD se cancelen parcialmente en un rango de niveles de señal, como se muestra en la Figura\(\PageIndex{4}\). Esto extiende el rango dinámico del sistema en cascada, y lo simple\(\text{OIP3}\) y\(\text{IIP3}\) las métricas no son suficientes para capturar esta complejidad.
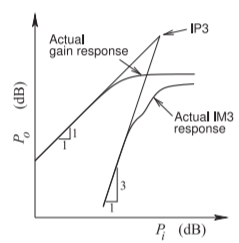
Figura\(\PageIndex{4}\): La ganancia y\(\text{IM3}\) las respuestas de dos etapas en cascada que muestran la cancelación parcial de la\(\text{IM3}\) respuesta en un rango de niveles de señal de entrada.
Ejemplo\(\PageIndex{3}\): Intermodulation Distortion of a Two-Stage Amplifier
La primera etapa de un amplificador de dos etapas en un transmisor tiene una ganancia de\(G_{1} = 20\text{ dB}\) y un punto de intercepción de tercer orden de salida,\(\text{OIP3}_{1}\), de\(30\text{ dBm}\). La segunda etapa tiene una ganancia de\(G_{2} = 20\text{ dB}\) y una\(\text{OIP3}\) de\(40\text{ dBm}\). Supongamos que las contribuciones IMD de cada etapa están en fase. ¿Cuál es el\(\text{OIP3}\) del sistema en cascada?
Solución
Usando el método de intercepción en cascada organizada, el total\(\text{OIP3}\),\(\text{OIP3}^{\text{T}}\), en milivatios se obtiene usando la ecuación\(\eqref{eq:10}\)
\[\label{eq:17}\left(\text{OIP3}^{\text{T}}\right)^{-\frac{1}{2}}\approx\left(10^{(20/10)}10^{(30/10)}\right)^{-\frac{1}{2}}+\left(10^{(40/10)}\right)^{-\frac{1}{2}}=(10^{5})^{-\frac{1}{2}}+(10^{4})^{-\frac{1}{2}} \]
Así
\[\label{eq:18}\text{OIP3}^{\text{T}}=5772\text{ mW}=37.6\text{ dBm} \]
Esta es la peor situación de los casos. Vale la pena comparar esto con un cálculo donde se desconocen las fases de las contribuciones del IMD. Luego, usando Ecuación\(\eqref{eq:14}\),
\[\label{eq:19}\left(\text{OIP3}^{\text{T}}\right)^{-1}\approx\left(10^{(20/10)}10^{(30/10)}\right)^{-1}+\left(10^{(40/10)}\right)^{-1}=10^{5}+10^{4} \]
Así
\[\label{eq:20}\text{OIP3}^{\text{T}}=9091\text{ mW}=39.6\text{ dBm} \]

